Punto de partida
En este post anterior se diseñó e implementó un reproductor de sonido para el Teensy que almacenaba un bucle en la memoria flash del microcontrolador. Se utilizó el DAC de 12 bits que viene de serie con el microcontrolador MK20 del Teensy y para el envío de muestras a dicho DAC se usó la interrupción periódica Systick, que traen de serie todos los microcontroladores ARM Cortex-M, ajustada a la frecuencia de muestreo.
void systick() __attribute__ ((section(".systick"))); void systick() { DACDAT = next sample } int main() { // configure DAC SIM_SCGC2 |= (1 << 12); // enable DAC clock generator DAC0_C1 = 0x00; // disable DAC DMA DAC0_C0 = 0xC0; // enable DAC for VREF2 (3.3v) // configure SYSTICK SYST_RVR = F_CPU / SAMPLE_RATE; SYST_CVR = 0; SYST_CSR |= 0x07; while (1) ; }
Objetivo
El objetivo planteado en este caso era implementar un pequeño sintetizador monofónico partiendo de ese mismo modelo (interrupción Systick + DAC). Los bloques planteados para el mini sintetizador son los siguientes:
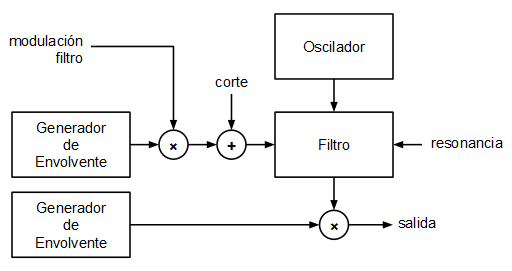
El oscilador
Se ha planteado un oscilador muy sencillo basado en tabla de ondas. Un oscilador basado en tabla de ondas consiste en uno o varios arrays con los valores de la onda que queremos generar, en cada array se guarda un único ciclo de onda y el oscilador lo que hace para emitir tonos a diferente frecuencia es recorrer dicha tabla a diferentes velocidades dando la vuelta cuando llega al final:
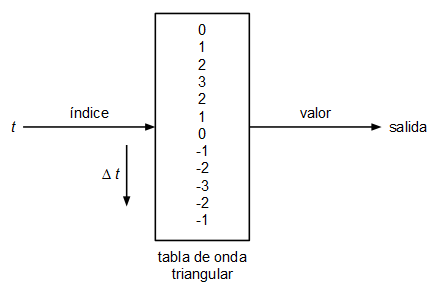
El tamaño de la tabla de ondas vendrá determinado por la resolución (calidad) que queramos darle y por la frecuencia de muestreo. Imaginemos que tenemos un array con 100 valores de una onda con forma de diente de sierra:
// 100 enteros con signo entre -50 y 49
[-50, -49, -48, -47, ... , 47, 48, 49]
Si la frecuencia de muestreo es de 44100 Hz (la frecuencia de muestreo estándar de calidad CD) y queremos reproducir un tono de 440 Hz (nota LA de la cuarta octava del piano) a partir de esta tabla de ondas el oscilador tendrá que usar un incremento de:
$$\Delta t = {440 \over {44100 \over 100}} = 0.9977324263$$
Esto es, el oscilador tomará la primera muestra de la posición 0 de la tabla, la siguiente muestra la tomará de la posición 0.9977324263, la siguiente de la posición 1.9954648526, y así sucesivamente. Como obviamente se trata de una tabla con posiciones enteras, en cada iteración se coge la muestra más próxima o se interpola.
En este caso se ha optado por usar la muestra en la posición de la parte entera del índice. No es la mejor forma de hacerlo pero sí la más rápida:
| t | índice (parte entera de t) |
|---|---|
| 0 | 0 |
| 0.9977324263 | 0 |
| 1.9954648526 | 1 |
| 2.9931972789 | 2 |
| 3.9909297052 | 3 |
| ... | |
| 99.77324263 | 99 |
| 100.7709750563 | |
| como la tabla mide 100, en este momento se vuelve a empezar, manteniendo la parte fraccionaria | |
| 0.7709750563 | 0 |
| 1.7687074826 | 1 |
| 2.7664399089 | 2 |
| ... | |
Debido a que estamos haciendo la implementación en un procesador sin unidad de coma flotante, se realizan todos los cálculos usando aritmética de punto fijo. El formato elegido es el Q16.16 (16 bits enteros + 16 bits fraccionarios = 32 bits que pueden alojarse en un tipo int32_t). Se definen, además, varias macros para facilitar la comprensión del código:
typedef int32_t fixedpoint_t; #define __FP_INTEGER_BITS 16 #define __FP_FRACTIONAL_BITS 16 #define __TO_FP(a) (((int32_t) (a)) << __FP_FRACTIONAL_BITS) #define __FP_1 (((int32_t) 1) << __FP_FRACTIONAL_BITS) #define __FP_ADD(a, b) (((int32_t) (a)) + ((int32_t) (b))) #define __FP_SUB(a, b) (((int32_t) (a)) - ((int32_t) (b))) #define __FP_MUL(a, b) ((int32_t) ((((int64_t) (a)) * ((int64_t) (b))) >> __FP_FRACTIONAL_BITS)) #define __FP_DIV(a, b) ((int32_t) ((((int64_t) (a)) << __FP_FRACTIONAL_BITS) / ((int64_t) (b))))
El código del método getNextSample del oscilador (el que se invoca para calcular cada muestra) queda, por tanto, como sigue:
fixedpoint_t Oscillator::getNextSample() { if (this->status == STATUS_STOPPED) return 0; else if (this->status == STATUS_STARTED) { fixedpoint_t v = ((fixedpoint_t) Wavetable::VALUES[this->t >> __FP_FRACTIONAL_BITS]); if (this->patch->waveform == OscillatorPatch::WAVEFORM_SQUARE) v = (v > 0) ? __TO_FP(1) : __TO_FP(-1); this->t = __FP_ADD(this->t, this->inc); if (this->t >= Wavetable::SIZE_FP) this->t = __FP_SUB(this->t, Wavetable::SIZE_FP); return v; } else return 0; }
Como se puede ver, el atributo t del objeto es el que se va incrementando y a la hora de determinar qué valor devuelve el método getNextSample() se usa como índice de la tabla simplemente la parte entera de t. Esta decisión no es gratuita e implica que hay que tratar de que los incrementos siempre sean mayores o iguales a 1 para que no se produzcan "escalones" en la señal de salida debido a que se repitan muestras de la tabla: en el ejemplo anterior la primera muestra (t = 0) y la segunda (t = 0.9977324263) serán la misma ya que la parte entera de ambos valores es 0. Para evitar que se produzcan estos escalones se ha optado por incrementar el tamaño de la tabla de ondas.
Si partimos de la base de que la frecuencia del tono es directamente proporcional al incremento de t, se puede buscar un tamaño de tabla tal que, para la frecuencia más baja que se quiera reproducir, se obtenga un incremento de t igual a 1. En efecto, si consideramos que no vamos a reproducir tonos por debajo de los 20 Hz (límite inferior del umbral de audición humano), definiendo las tablas de ondas con un tamaño de
$${44100 \over 20} = 2205 \thinspace muestras$$
Para cualquier tono que queramos reproducir, tendremos siempre un incremento de t mayor o igual a 1. Por otro lado podemos simplificar la ecuación del cálculo del incremento de t:
$$\Delta t = {f_{tono} \over 20}$$
Debido a que el propio cálculo del incremento de t implica una división y las divisiones consumen gran cantidad de recursos en procesadores sin unidad de división (como es el caso del ARM Cortex-M) se ha optado por meter en una tabla los diferentes valores del incremento de t. El índice de dicha tabla es el índice de la nota MIDI (entre 0 y 127).
const fixedpoint_t Wavetable::MIDI_FREQ_INC[128] = { 0, 28384, 30071, 31859, 33754, 35761, 37887, 40140, 42527, 45056 ... 34563955, 36619234, 38796727, 41103701 };
Con esta tabla precalculada sintonizar el oscilador solo requiere una indexación y una asignación:
void Oscillator::noteOn(uint8_t midiKey, uint8_t midiVelocity) { this->inc = Wavetable::MIDI_FREQ_INC[midiKey]; this->status = STATUS_STARTED; }
Generador de envolvente
Se utilizan dos generadores de envolvente independientes. Uno que modula la frecuencia de corte del filtro y otro que modula la amplitud del sonido final, antes de escribirlo en el DAC. El tipo de envolvente más común y el que se ha utilizado en este caso es el tipo ADSR (Attack-Decay-Sustain-Release). Cada envolvente de este tipo posee tres valores característicos: el tiempo de ataque (A), el tiempo de caída (D), el nivel de sostenido (S) y el tiempo de liberación (R). Se puede ver un generador de envolvente como una generador de una señal muy lenta que varía entre 0 y 1.
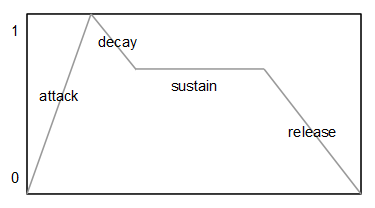
Si se define un nivel de sostenido igual a 0, tenemos una envolvente de tipo AD (Attack-Decay).
Aunque lo más común es definir los parámetro A, D y R en unidades de tiempo (milisegundos, microsegundos), en este caso se ha optado por indicar dichos valores en forma de incrementos, de esta forma no es necesario realizar ninguna multiplicación ni división por cada muestra que se calcula.
fixedpoint_t EnvelopeGenerator::getNextSample() { uint8_t localStatus = this->status; fixedpoint_t ret = 0; do { this->status = localStatus; if (localStatus == STATUS_STOP) ret = 0; else if (localStatus == STATUS_ATTACK) { ret = this->lastSample + this->patch->attackInc; if (ret >= __TO_FP(1)) { ret = __TO_FP(1); localStatus = STATUS_DECAY; } } else if (localStatus == STATUS_DECAY) { ret = this->lastSample - this->patch->decayInc; if (ret <= this->patch->sustainLevel) { ret = this->patch->sustainLevel; if (ret == 0) localStatus = STATUS_STOP; else localStatus = STATUS_SUSTAIN; } } else if (localStatus == STATUS_SUSTAIN) { ret = this->patch->sustainLevel; if (this->noteOffReceived) { this->noteOffReceived = false; localStatus = STATUS_RELEASE; } } else if (localStatus == STATUS_RELEASE) { ret = this->lastSample - this->patch->releaseInc; if (ret <= 0) { ret = 0; localStatus = STATUS_STOP; } } } while (localStatus != this->status); this->lastSample = ret; return __FP_MUL(ret, this->amplitude); }
En la fase de ataque (A) se va incrementando la señal de salida desde 0 hasta 1 en pasos attackInc, en la fase de caída (D) se va decrementando la señal de salida desde 1 hasta el nivel de sostenido en pasos decayInc. Si el nivel de sostenido es 0 la envolvente para al terminar la fase de caída (D), en caso contrario mantiene el nivel de sostenido hasta que se invoca el método noteOff. En ese momento se inicia la fase de liberación (R) decrementando la señal de salida desde el nivel de sostenido hasta 0 en pasos releaseInc.
Filtro
A la hora de implementar un filtro digital existen diferentes aproximaciones: discretización de filtros analógicos conocidos, diseño digital directo usando diagrama de polos y ceros, etc. En este caso se ha optado por una conocida implementación publicada en el libro “Musical Applications of Microprocessors” de Hal Chamberlin. Se trata de una implementación en digital de un filtro de estado variable que permite extraer señales paso bajo, paso banda, paso alto y elimina banda utilizando muy pocos cálculos.
Dicho filtro viene caracterizado por el siguiente sistema de ecuaciones en diferencias:
$$pasoAlto[n] = entrada - ({r \times pasoBanda[n-1]}) - pasoBajo[n]$$
$$pasoBanda[n] = ({f \times pasoAlto[n]}) + pasoBanda[n - 1]$$
$$pasoBajo[n] = ({f \times pasoBanda[n - 1]}) + pasoBajo[n - 1]$$
Siendo:
$$f = 2\sin\left({\pi F_c \over F_s}\right)$$
$$r = {1 \over Q}$$
Siendo $F_c$ la frecuencia de corte del filtro, $F_s$ la frecuencia de muestreo y $Q$ la Q del filtro (la resonancia).
Si se reordenan las ecuaciones en diferencias:
$$pasoBajo[n] = ({f \times pasoBanda[n - 1]}) + pasoBajo[n - 1]$$
$$pasoAlto[n] = entrada - ({r \times pasoBanda[n - 1]}) - pasoBajo[n]$$
$$pasoBanda[n] = ({f \times pasoAlto[n]}) + pasoBanda[n - 1]$$
Podemos olvidarnos de los índices:
pasoBajo += f * pasoBanda
pasoAlto = entrada - (r * pasoBanda) - pasoBajo
pasoBanda += f * pasoAlto
Como se puede apreciar es preciso mantener en memoria al menos las variables “pasoBajo” y “pasoBanda” entre que se procesa una muestra y la siguiente (se trata de un filtro digital de segundo orden).
fixedpoint_t StateVariableFilter::getNextSample(fixedpoint_t input) { this->lowPass = __FP_ADD(this->lowPass, __FP_MUL(this->cutoff, this->bandPass)); fixedpoint_t highPass = __FP_SUB(__FP_SUB(input, this->lowPass), __FP_MUL(this->resonance, this->bandPass)); this->bandPass = __FP_ADD(this->bandPass, __FP_MUL(this->cutoff, highPass)); if (this->mode == MODE_LOWPASS) return this->lowPass; else if (this->mode == MODE_BANDPASS) return this->bandPass; else if (this->mode == MODE_HIGHPASS) return highPass; else if (this->mode == MODE_NOTCH) return __FP_ADD(highPass, this->lowPass); return 0; }
Voz
En la clase Voice juntamos los elementos que se han definido hasta ahora. Esta clase implementa también la interface Generator:
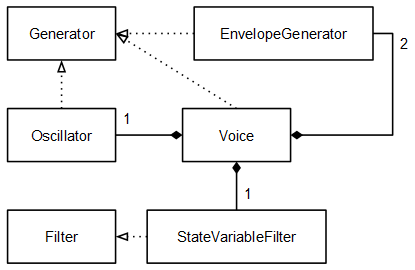
void Voice::noteOn(uint8_t midiKey, uint8_t midiVelocity) { this->oscillator.noteOn(midiKey, midiVelocity); this->ampEnv.noteOn(midiKey, midiVelocity); this->filterEnv.noteOn(midiKey, midiVelocity); } void Voice::noteOff(uint8_t midiKey) { this->oscillator.noteOff(midiKey); this->ampEnv.noteOff(midiKey); this->filterEnv.noteOff(midiKey); } fixedpoint_t Voice::getNextSample() { fixedpoint_t o = this->oscillator.getNextSample(); fixedpoint_t env = __FP_MUL(this->filterEnv.getNextSample(), this->filterEnvMod); fixedpoint_t cutoff = __FP_ADD(env, this->cutoff); if (cutoff < 0) cutoff = 0; else if (cutoff > __TO_FP(1)) cutoff = __TO_FP(1); this->filter.cutoff = cutoff; fixedpoint_t aux = this->filter.getNextSample(o); fixedpoint_t e = this->ampEnv.getNextSample(); return __FP_MUL(aux, e); }
Ahora cada objeto Voice es un sintetizador monofónico. Si en un futuro se quisiese implementar un sintetizador polifónico simplemente habría que instanciar tantos objetos Voice como voces de polifonía se quisieran.
Secuenciador
Aunque en el diagrama inicial no aparece, es fundamental implementar un secuenciador si se quiere probar el sintetizador y no podemos o no queremos pelearnos aún con la implementación de una entrada MIDI. El secuenciador se encarga de disparar notas en determinados instantes de tiempo, en otras palabras, es el objeto que “toca” el instrumento.
En este caso se ha optado por la implementación de un sencillo secuenciador de 16 pasos equidistantes en semicorcheas. 16 semicorcheas forman un compás de 4 por 4 por lo que toca un único compás. El secuenciador vuelve al empezar cuando llega al final: después de tocar la nota de la semicorchea 15, empieza de nuevo en la semicorchea 0.
void Sequencer::setBPM(uint16_t bpm) { uint32_t stepsPerMinute = bpm * 4; // semicorcheas (pasos de secuenciador) por minuto this->n = (Generator::SAMPLES_MS * ((uint32_t) 60000)) / stepsPerMinute; // muestras por semicorchea }
Como el método run se invoca cada vez que se va a generar una muestra (SAMPLE_RATE veces por segundo) se disparará una nota cada vez que un contador interno llegue a n.
void Sequencer::run() { if (this->status == STATUS_PLAY) { if (this->t == 0) { uint8_t note = this->midiNote[this->nextNoteIndex]; if ((note > 0) && (this->generator != NULL)) this->generator->noteOn(note, 100); this->nextNoteIndex++; if (this->nextNoteIndex == SEQUENCE_SIZE) this->nextNoteIndex = 0; } this->t++; if (this->t == this->n) this->t = 0; } }
Nótese que el secuenciador no envía eventos de tipo “noteOff”. Esto está hecho así adrede para este caso concreto por simplicidad, y porque las envolventes que se usan tienen siempre el nivel de sostenido a 0 (el sonido se acaba extinguiendo aunque el secuenciador no envíe eventos “noteOff”). Como la clase Voice implementa la interface Generator, le podemos decir al secuenciador que mande los disparos de nota (“noteOn”) al objeto de tipo Voice:
Voice v;
Sequencer seq;
...
seq.setBPM(120);
seq.setGenerator(v);
De esta forma ya tenemos adecuadamente inicializado el secuenciador. Ahora sólo falta meter las notas MIDI que queramos que toque. Un valor de nota igual a 0 indica al secuenciador que no queremos disparar ninguna nota en esa semicorchea:
seq.midiNote[0] = 36; // Do 1 seq.midiNote[1] = 24; // Do 0 seq.midiNote[2] = 0; seq.midiNote[3] = 36; // Do 1 seq.midiNote[4] = 39; // Re# 1 seq.midiNote[5] = 0; seq.midiNote[6] = 0; seq.midiNote[7] = 39; // Re# 1 seq.midiNote[8] = 36; // Do 1 seq.midiNote[9] = 24; // Do 0 seq.midiNote[10] = 0; seq.midiNote[11] = 36; // Do 1 seq.midiNote[12] = 39; // Re# 1 seq.midiNote[13] = 0; seq.midiNote[14] = 0; seq.midiNote[15] = 43; // Sol 1 seq.start(); // cambiamos el estado interno del secuenciador a STATUS_PLAY
En este caso se ha metido una sencilla secuencia típica de música electrónica, en la escala de Do menor.
Juntándolo todo
El secuenciador invoca al método “noteOn” del objeto Voice cada vez que hay una nota nueva que tocar y el valor devuelto por el método “getNextSample” del objeto de tipo Voice es el que se manda al DAC. La señal debe ser adaptada de fixedpoint_t a entero sin signo de 12 bits (0 - 4095):
void systick() { seq.run(); fixedpoint_t aux = v.getNextSample() >> 1; // evitar clipping uint16_t out; if (aux >= __TO_FP(1)) out = 4095; else if (aux <= __TO_FP(-1)) out = 0; else out = (uint16_t) (((aux + 32768) >> 4) & 0x00000FFF); DACDAT = out; }
Resultados
En la implementación final realizada se ha optado por utilizar una frecuencia de muestreo de 32 KHz. Usar esta frecuencia de muestreo permite generar tonos más precisos ya que 96 MHz no es divisible entre 44.1 KHz pero sí lo es entre 32 KHz (la frecuencia de muestreo es más precisa a 32 KHz que a 44.1 KHz).
A continuación un vídeo en el que puede verse y oirse el invento. No se oye muy alto porque tuve que poner el volumen bajo (era tarde cuando grabé) y encima pasó un camión en ese momento por la calle ¬¬
Todo el código fuente está disponible en la sección soft.
[ añadir comentario ] ( 2261 visualizaciones ) | [ 0 trackbacks ] | enlace permanente | enlace relacionado |




 ( 3 / 3467 )
( 3 / 3467 )El procesador ARM Cortex-M4 (Un MK20DX256 de Freescale) incluido en la placa de desarrollo Teensy 3.1 viene equipado con una salida analógica (DAC, no PWM) de 12 bits de resolución con la que es posible generar audio con una calidad razonable y sin apenas hardware externo.
Punto de partida
Se parte del compilador gcc, las binutils y la newlib compilados para el target “arm-none-eabi” detallados en este post y del trabajo realizado anteriormente en este otro post.
DAC
El DAC del microcontrolador Freescale MK20DX256 tiene una resolución de 12 bits (sin signo) y puede ser utilizado tanto de forma sencilla como mediante DMA. En este caso se va a optar por un uso sencillo sin DMA: La escritura de los datos de las muestras la hará el propio código del programa.
... #define SIM_SCGC2 *((uint32_t *) 0x4004802C) #define DACDAT *((uint16_t *) 0x400CC000) #define DAC0_C0 *((uint8_t *) 0x400CC021) #define DAC0_C1 *((uint8_t *) 0x400CC022) ... SIM_SCGC2 |= (1 << 12); // habilitar el generador de reloj para el DAC DAC0_C1 = 0x00; // deshabilitar el modo DMA para el DAC DAC0_C0 = 0xC0; // habilitar el DAC para VREF2 (3.3v) // a partir de ahora ya se puede escribir en el DAC (DACDAT) ...
Hay que tener en cuenta que el registro DACDAT es un registro de 12 bits sin signo (unsigned).
Systick
La interrupción “systick” es una de las interrupciones estándar del núcleo ARM Cortex-M4 (de hecho está presente en todos los procesadores ARM Cortex). Se trata de una interrupción que se dispara cuando un contador de 24 bits llega a cero, dicho contador está gobernado por el reloj del núcleo (cuidado, suele ser diferente al reloj del bus) y carece de divisores (es muy simple).
El vector de la interrupción se encuentra en la dirección de memoria 0x0000003C. En esta dirección de memoria debe alojarse la dirección de memoria donde se encuentre la función que se ejecutará cada vez que el systick llegue a cero y vuelva a cargarse (una indirección).
Para implementar esta funcionalidad con el GCC se modifica el linker script (teensy31.ld) para incluir el nuevo vector de interrupción:
...
. = 0x00000000 ;
.cortex_m4_vectors : {
LONG(0x20007FFC);
LONG(0x00000411);
}
. = 0x0000003C ;
.cortex_m4_vector_systick : {
LONG(SYSTICK_ADDRESS + 1);
}
. = 0x00000400 ;
.flash_configuration : {
LONG(0xFFFFFFFF);
LONG(0xFFFFFFFF);
LONG(0xFFFFFFFF);
LONG(0xFFFFFFFE);
}
...
Y para incluir una nueva sección dentro de la memoria de programa con una dirección de memoria prefijada:
...
SYSTICK_ADDRESS = . ;
.systick : {
*(.systick)
}
...
Nótese que la dirección de memoria almacenada en 0x0000003C es la siguiente dirección impar después de SYSTICK_ADDRESS. Esto tiene una explicación y es muy sencilla:
Los procesadores ARM soportan dos repertorios de instrucciones: un repertorio muy amplio y potente en el que cada instrucción ocupa 32 bits (modo “arm”) y otro repertorio más reducido en el que cada instrucción ocupa 16 bits (modo “thumb”). El primero es más potente pero ocupa más, mientras que el segundo en menos potente pero ocupa mucho menos. Lo que se puede hacer en modo “arm” se puede hacer también en modo “thumb” aunque es posible que para hacer lo que hace una instrucción “arm” sean necesarias dos o tres instrucciones “thumb”.
La forma en que un procesador ARM sabe si una instrucción a la que apunta el PC forma parte de un repertorio de instrucciones u otro es mediante el bit 0 del PC. Si el bit 0 vale 0, se trata de una instrucción “arm”, mientras que si el bit vale 1 se trata de una instrucción “thumb” (nótese que sea cual sea el modo, todas las instrucciones se encuentran, como mínimo, en direcciones pares, en las direcciones impares nunca hay instrucciones).
Por otro lado según la especificación ARM, las excepciones (interrupciones) se deben ejecutar siempre en modo “thumb”. De todas formas en este caso no tenemos elección ya que la serie Cortex-M de ARM sólo soporta el repertorio de instrucciones “thumb” (http://infocenter.arm.com/help/index.jsp?topic=/com.arm.doc.dui0553a/CHDBIBGJ.html).
Con la nueva sección de código llamada “.systick” en el código fuente puede ahora definirse la función que va a manejar la interrupción:
... #define SYST_CSR *((uint32_t *) 0xE000E010) #define SYST_RVR *((uint32_t *) 0xE000E014) #define SYST_CVR *((uint32_t *) 0xE000E018) #define SAMPLE_RATE 44100 // indicamos al compilador que queremos alojar el cuerpo de esta función en la sección “.systick” void systick() __attribute__ ((section(".systick"))); void systick() { // TODO } ... ... // configuramos el systick para que se ejecute SAMPLE_RATE veces por segundo SYST_RVR = F_CPU / SAMPLE_RATE; SYST_CVR = 0; SYST_CSR |= 0x07; ...
F_CPU es la velocidad en Hz del núcleo (en este caso 96 MHz = 96000000 Hz) y hacemos que el systick se ejecute 44100 veces por segundo (la frecuencia de muestreo del sonido a reproducir).
No se debe utilizar el atributo “interrupt” al declarar la función “systick” ya que en ese caso el compilador intenta compilarla en modo “arm” en lugar de “thumb”.
Sonido
Partiendo de uno de los sonidos (un bucle de bateria) publicado con licencia Creative Commons Attribution-ShareAlike por el usuario de Soundcloud “Phantom Hack3r” (AKA Loop Studio, https://soundcloud.com/phantom-hack3r) se ha editado, se ha dejado sólo con un único compás (el inicial) y se ha exportado a WAV (“drum_loop_1.wav”).
A continuación, usando la herramienta de línea de comandos, “sox” se exporta a su vez este fichero WAV a un formato crudo de 8 bits, mono y sin signo:
sox drum_loop_1.wav -u -b 8 -c 1 -r 44100 drum_loop_1.rawLuego el fichero drum_loop_1.raw se convierte a un fichero objeto para meterlo como si fuese código dentro del microcontrolador:
/opt/teensy/bin/arm-none-eabi-objcopy --input binary --output elf32-littlearm --binary-architecture arm --rename-section .data=.text drum_loop_1.raw drum_loop_1.oLa opción “--rename-section .data=.text” es muy importante ya que marca los datos generados para que se alojen en la sección “.text” del fichero de salida. Esta sección es la sección que será alojada en la memoria flash del Teensy.
Ahora en “drum_loop_1.o” hay definidas dos variables “_binary_drum_loop_1_raw_start” y “_binary_drum_loop_1_raw_end” cuya dirección de memoria es el inicio y el final respectivamente de los datos crudos convertidos (“drum_loop_1.raw”).
Circuito de salida
A la hora de conectar la salida analógica del DAC a unos altavoces hay que hacerlo siempre a través de un amplificador ya que la corriente máxima que soporta la salida DAC es muy baja. De entre todas las opciones de amplificación, la más sencilla es, sin duda, el uso de unos altavoces amplificados de PC (solución sugerida por el propio creador del Teensy, Paul Stoffregen, aquí).
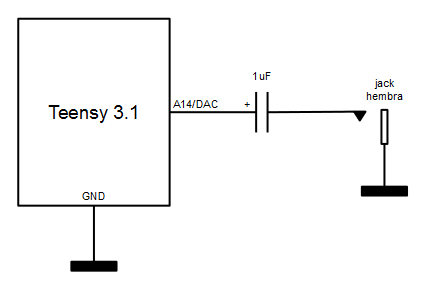
Se trata de un sencillo condensador electrolítico (para el desacoplo de continua) entre la salida del DAC y la entrada del amplificador de altavoces.
Resultado final
El código fuente final de main.cc es el siguiente:
#include <stdint.h> using namespace std; #define SYST_CSR *((uint32_t *) 0xE000E010) #define SYST_RVR *((uint32_t *) 0xE000E014) #define SYST_CVR *((uint32_t *) 0xE000E018) #define SIM_SCGC2 *((uint32_t *) 0x4004802C) #define DACDAT *((uint16_t *) 0x400CC000) #define DAC0_C0 *((uint8_t *) 0x400CC021) #define DAC0_C1 *((uint8_t *) 0x400CC022) #define SAMPLE_RATE 44100 extern char _binary_drum_loop_1_raw_start; extern char _binary_drum_loop_1_raw_end; volatile char *p; void systick() __attribute__ ((section(".systick"))); void systick() { DACDAT = ((uint16_t) *p) << 4; p++; if (p == &_binary_drum_loop_1_raw_end) p = &_binary_drum_loop_1_raw_start; } int main() { // configure DAC SIM_SCGC2 |= (1 << 12); // enable DAC clock generator DAC0_C1 = 0x00; // disable DAC DMA DAC0_C0 = 0xC0; // enable DAC for VREF2 (3.3v) // configure SYSTICK p = &_binary_drum_loop_1_raw_start; SYST_RVR = F_CPU / SAMPLE_RATE; SYST_CVR = 0; SYST_CSR |= 0x07; while (1) ; }
A continuación un vídeo donde puede verse (y oírse) el montaje en funcionamiento.
Todo el código fuente puede descargarse de la sección soft.
[ añadir comentario ] ( 2371 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 15944 )
( 3 / 15944 )En vista de la repentina desaparición del contenido de la web http://kunen.org/uC/gnu_tool.html (“Building the GNU ARM Toolchain for Bare Metal”) que se usó como referencia en este post y en la que se explicaba con gran detalle y facilidad cómo compilar la toolchain de GNU para el target arm-none-eabi, he decidido poner aquí los pasos que di yo (basados en los ahora desaparecidos) para compilar dicha toolchain (yo lo hice para las versiones binutils-2.25, gcc-5.1.0 y snapshot 20150423 de newlib).
Me he basado en los pasos descritos en la web desaparecida y en la web http://wiki.osdev.org/GCC_Cross-Compiler#GCC.
Hay que asegurarse de que se encuentran instalados los paquetes: textinfo, zlib-devel, flex, bison y el resto de herramientas de compilación (gcc, autoconf, etc.). Es recomendable hacer todos los pasos como usuario root.
Descarga
mkdir -p /opt/teensy/src
cd /opt/teensy/src
binutils 2.25
wget ftp://ftp.gnu.org/gnu/binutils/binutils-2.25.tar.bz2
tar xjf binutils-2.25.tar.bz2
gcc 5.1.0
wget ftp://ftp.gnu.org/gnu/gcc/gcc-5.1.0/gcc-5.1.0.tar.bz2
wget https://gmplib.org/download/gmp/gmp-6.0.0a.tar.bz2
wget http://www.mpfr.org/mpfr-current/mpfr-3.1.2.tar.bz2
wget ftp://ftp.gnu.org/gnu/mpc/mpc-1.0.3.tar.gz
wget http://isl.gforge.inria.fr/isl-0.14.tar.bz2
tar xjf gcc-5.1.0.tar.bz2
tar xjf gmp-6.0.0a.tar.bz2
tar xjf isl-0.14.tar.bz2
tar xzf mpc-1.0.3.tar.gz
tar xjf mpfr-3.1.2.tar.bz2
mv gmp-6.0.0 gcc-5.1.0/gmp
mv isl-0.14 gcc-5.1.0/isl
mv mpc-1.0.3 gcc-5.1.0/mpc
mv mpfr-3.1.2 gcc-5.1.0/mpfr
newlib
wget ftp://sourceware.org/pub/newlib/newlib-2.2.0.20150423.tar.gz
tar xzf newlib-2.2.0.20150423.tar.gz
Compilación
binutils 2.25
mkdir -p /opt/teensy/build/binutils-2.25
cd /opt/teensy/build/binutils-2.25
../../src/binutils-2.25/configure --target=arm-none-eabi --prefix=/opt/teensy --enable-interwork --enable-multilib
make
make install
export PATH="/opt/teensy/bin:$PATH"
gcc 5.1.0 (inicial)
mkdir -p /opt/teensy/build/gcc-5.1.0
cd /opt/teensy/build/gcc-5.1.0
../../src/gcc-5.1.0/configure --target=arm-none-eabi --prefix=/opt/teensy --enable-interwork --enable-multilib --enable-languages="c,c++" --with-newlib --with-headers=../../src/newlib-2.2.0.20150423/newlib/libc/include --with-system-zlib
make all-gcc
make install-gcc
newlib
mkdir -p /opt/teensy/build/newlib
cd /opt/teensy/build/newlib
../../src/newlib-2.2.0.20150423/configure --target=arm-none-eabi --prefix=/opt/teensy --enable-interwork --enable-multilib
make
make install
gcc 5.1.0 (final)
cd /opt/teensy/build/gcc-5.1.0
make all
make install
Tras completar todo el proceso, el compilador, las binutils y la newlib para ARM quedan instaladas en la carpeta /opt/teensy.
[ añadir comentario ] ( 1911 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 3848 )
( 3 / 3848 )Las FPGAs y los CPLDs son circuitos integrados digitales programables a nivel hardware mediante algún tipo de lenguaje de descripción de hardware (VHDL, Verilog, SystemC, etc.). A lo largo de este post se desarrolla una primera toma de contacto con este tipo de integrados.
FPGA
La FPGA que se ha usado es una Xilinx Spartan 3E, que se puede encontrar en la placa Papilio One (http://papilio.cc). Esta placa es open hardware, con interface USB, memoria flash SPI para almacenar la configuración del hardware y con una buena relación calidad/precio (unos 38 dólares aproximadamente).
El entorno de desarrollo de Xilinx es un poco complejo (muchas opciones) pero se le coge el truco rápido. Es gratuito (aunque no es software libre) y muy fácil de instalar tanto en Windows como en Linux (no está para Mac). El entorno de desarrollo permite gestionar proyectos en VHDL o Verilog y generar al final los ficheros ".bit" que son los que se mandan a la FPGA.
De http://papilio.cc se descarga el Papilio Loader, un software open source que permite "tostar" los ficheros ".bit" en la placa FPGA y probar los diseños rápidamente. En la propia página del proyecto vienen varios tutoriales.
Prueba de concepto
Como prueba inicial se plantea un circuito conversor de binario (4 bits, del 0 al 9) a 7 segmentos mediante interfaz serie:
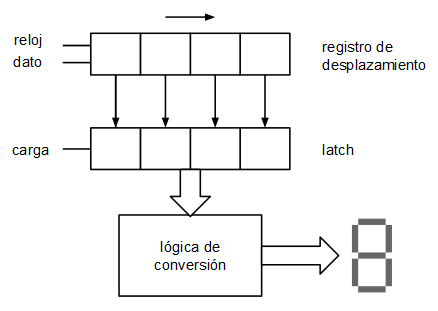
Se trata de un esquema muy sencillo: un registro de desplazamiento de 4 bits (que permite leer la entrada serie), un latch de 4 bits que carga el contenido del registro de desplazamiento y a la salida del latch una lógica combinatoria que convierte el número de 4 bits en una salida de 7 bits (para el display de 7 segmentos).
VHDL de la lógica combinatoria
VHDL es un lenguaje de descripción de hardware, no un lenguaje imperativo al uso. Cada línea de código describe un comportamiento y la única forma de realizar procesamiento secuencial es mediante la cláusula "process" ya que por defecto se ejecuta "todo a la vez".
Una lógica combinatoria está basada en puertas lógicas y las puertas lógicas se "ejecutan" siempre, no son como los biestables u otros elementos secuenciales. Para la lógica combinatoria de conversión binario a 7 segmentos se puede utilizar la sentencia WHEN...ELSE:
B(0) <= '1' when ((x = "0000") or (x = "0001") or (x = "0011") or (x = "0100") or (x = "0101") or (x = "0110") or (x = "0111") or (x = "1000") or (x = "1001")) else '0'; B(1) <= '1' when ((x = "0000") or (x = "0010") or (x = "0011") or (x = "0101") or (x = "0110") or (x = "1000") or (x = "1001")) else '0'; B(2) <= '1' when ((x = "0000") or (x = "0010") or (x = "0110") or (x = "1000")) else '0'; B(3) <= '1' when ((x = "0000") or (x = "0010") or (x = "0011") or (x = "0101") or (x = "0110") or (x = "0111") or (x = "1000") or (x = "1001")) else '0'; B(4) <= '1' when ((x = "0000") or (x = "0001") or (x = "0010") or (x = "0011") or (x = "0100") or (x = "0111") or (x = "1000") or (x = "1001")) else '0'; B(5) <= '1' when ((x = "0000") or (x = "0100") or (x = "0101") or (x = "0110") or (x = "1000") or (x = "1001")) else '0'; B(6) <= '1' when ((x = "0010") or (x = "0011") or (x = "0100") or (x = "0101") or (x = "0110") or (x = "1000") or (x = "1001")) else '0';
Como se puede apreciar en este caso, las 7 líneas de código debe "ejecutarse" de forma concurrente. Dicho de otra forma: se describen 7 circuitos combinacionales que deben implementarse en paralelo.
En este caso x es la salida del latch mientras que B es la salida de la FPGA que está conectada al display de 7 segmentos. En este caso se ha usado un display de cátodo común por lo que para encender un segmento del display hay que emitir un ‘1’ en la salida correspondiente.
VHDL de la lógica secuencial
La lógica secuencial se divide en la lógica del registro de desplazamiento que se ha implementado utilizando el clásico modelo RTL:
d_reg <= data_in & q_reg(3 downto 1); --d_reg es q_reg desplazado concatenado con el bit que hay en data_in process(clock_in) --el proceso se activa cuando clock_in cambia begin if (rising_edge(clock_in)) then --cuando hay un flanco de subida q_reg <= d_reg; --se carga d_reg en q_reg end if; end process;
Y la lógica del latch de 4 bits, que se encarga de cargar el registro de desplazamiento (q_reg) en la señal de entrada de la lógica combinatoria para la salida de 7 segmentos (x), y que también se ha implementado utilizando el modelo RTL:
process(latch_in) --el proceso se activa cuando latch_in cambia begin if (rising_edge(latch_in)) then --cuando hay un flanco de subida x <= q_reg; --se carga q_reg en x end if; end process;
En este caso las acciones a realizar no se hacen "siempre" sino que dependen de otras señales (clock_in y latch_in) y debe hacerse una evaluación secuencial (si ocurre esto entonces aquello), por eso se utilizan bloques "process". Nótese que ambos bloques "process" se "ejecutan" en paralelo.
VHDL completo
El código VHDL completo, incluyendo la arquitectura y el port queda como sigue:
library IEEE; use IEEE.STD_LOGIC_1164.ALL; use IEEE.STD_LOGIC_ARITH.ALL; use IEEE.STD_LOGIC_UNSIGNED.ALL; entity SimpleShiftRegister is port ( clock_in : in std_logic; data_in : in std_logic; latch_in : in std_logic; B : out std_logic_vector(6 downto 0) ); end SimpleShiftRegister; architecture behavioral of SimpleShiftRegister is signal d_reg : std_logic_vector(3 downto 0); signal q_reg : std_logic_vector(3 downto 0); signal x : std_logic_vector(3 downto 0); begin d_reg <= data_in & q_reg(3 downto 1); B(0) <= '1' when ((x = "0000") or (x = "0001") or (x = "0011") or (x = "0100") or (x = "0101") or (x = "0110") or (x = "0111") or (x = "1000") or (x = "1001")) else '0'; B(1) <= '1' when ((x = "0000") or (x = "0010") or (x = "0011") or (x = "0101") or (x = "0110") or (x = "1000") or (x = "1001")) else '0'; B(2) <= '1' when ((x = "0000") or (x = "0010") or (x = "0110") or (x = "1000")) else '0'; B(3) <= '1' when ((x = "0000") or (x = "0010") or (x = "0011") or (x = "0101") or (x = "0110") or (x = "0111") or (x = "1000") or (x = "1001")) else '0'; B(4) <= '1' when ((x = "0000") or (x = "0001") or (x = "0010") or (x = "0011") or (x = "0100") or (x = "0111") or (x = "1000") or (x = "1001")) else '0'; B(5) <= '1' when ((x = "0000") or (x = "0100") or (x = "0101") or (x = "0110") or (x = "1000") or (x = "1001")) else '0'; B(6) <= '1' when ((x = "0010") or (x = "0011") or (x = "0100") or (x = "0101") or (x = "0110") or (x = "1000") or (x = "1001")) else '0'; process(clock_in) begin if (rising_edge(clock_in)) then q_reg <= d_reg; end if; end process; process(latch_in) begin if (rising_edge(latch_in)) then x <= q_reg; end if; end process; end behavioral;
Tras compilar y sintetizar este código, la implementación eléctrica generada es la siguiente:
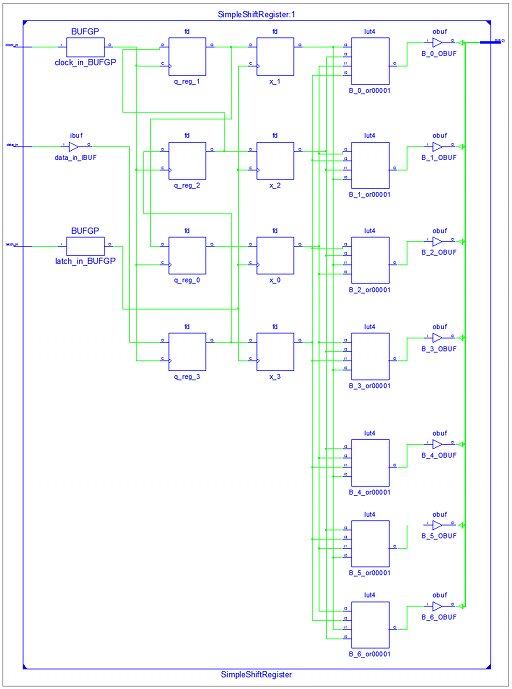
Como se puede ver, tanto el registro de desplazamiento como el latch se implementa mediante biestables D mientras que la lógica combinatoria de conversión de binario a 7 segmentos se implementa mediante LUTs (Look Up Tables), en lugar de mediante puertas lógicas. Esta forma de implementar lógica combinatoria es muy habitual en las FPGAs y los CPLDs.
Conexión con el Arduino
La FPGA funciona a 3.3 voltios mientras que el Arduino funciona a 5 voltios. Es necesario, por tanto adaptar los voltajes. En este caso concreto todas las señales salen del Arduino y entran en la FPGA por lo que se ha optado por hacer una adaptación de voltaje sencilla basada en transistores.
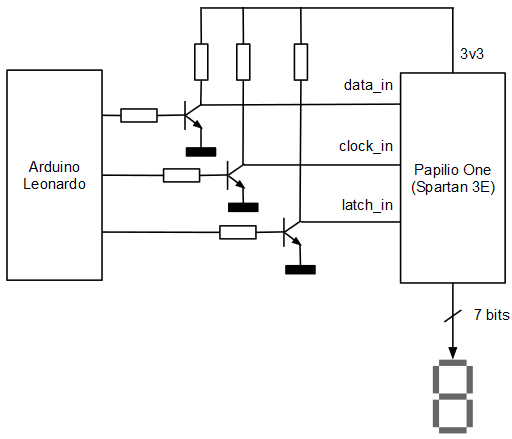
En el Arduino la función encargada de enviar un valor al display de 7 segmentos deberá colocar los datos de forma serie a través del pin data_in usando como reloj clock_in. Se activará latch_in cuando se desee mostrar en el display el valor cargado en el registro de desplazamiento. Obsérvese que al hacer la conversión de voltajes utilizando transistores NPN en configuración de emisor común, la lógica debe ser negada, es decir, para emitir un 1 de 3.3 voltios, emitimos un 0 de 5 voltios y para emitir un 0 de 3.3 voltios, emitimos un 1 de 5 voltios:
const int CLK_PIN = 0; const int DATA_PIN = 1; const int LATCH_PIN = 2; #define ONE LOW #define ZERO HIGH void byteOut(unsigned char v) { for (unsigned char i = 0; i < 4; i++) { if ((v & 1) != 0) digitalWrite(DATA_PIN, ONE); else digitalWrite(DATA_PIN, ZERO); delay(1); digitalWrite(CLK_PIN, ONE); delay(1); digitalWrite(CLK_PIN, ZERO); delay(1); v = v >> 1; } digitalWrite(LATCH_PIN, ONE); delay(1); digitalWrite(LATCH_PIN, ZERO); delay(1); }
A continuación puede verse un vídeo con el invento en funcionamiento:
Algunos enlaces para empezar con VHDL (en español)
Lista de reproducción de YouTube del profesor Carlos Fajardo sobre VHDL - Vídeos muy amenos y fáciles de seguir.
Libro online "Programación en VHDL" - Muy buen libro, aunque le echo en falta más ejemplos y ejercicios.
[ añadir comentario ] ( 2456 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 4389 )
( 3 / 4389 )La utilización de lógica borrosa o difusa (“fuzzy”) para el control de procesos permite abordar este tipo de problemas desde una perspectiva más "humana" ya que las reglas de la lógica borrosa son enunciados fácilmente comprensibles por una persona ajena a la teoría del control y su ajuste es más intuitivo que en el caso de controladores más "puros" como el PID. A lo largo de este post se abordará el control de velocidad de un sencillo motor DC mediante lógica borrosa utilizando sólo un puñado de reglas.
El problema
Se parte de un lazo de control estándar, el mismo que se utilizó cuando se implementó el control PID:
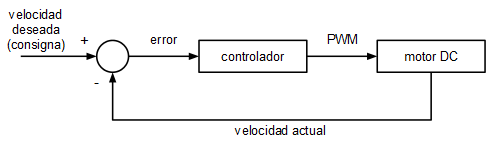
La velocidad se lee mediante un sencillo encoder compuesto por un disco pintado mitad de blanco y mitad de negro y por un sensor infrarrojo de tipo reflexivo (el CNY70, de los que suelen usarse en robots siguelineas).
El motor es accionado a través de una de las salidas PWM del microcontrolador mediante un transistor NPN de potencia.
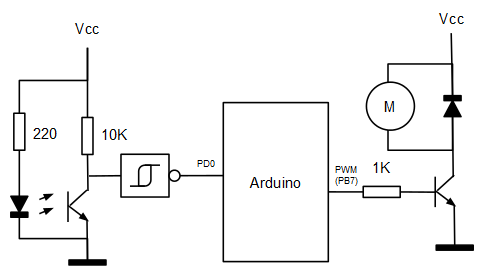
El esquema es exactamente el mismo que el utilizado en el post anterior.
Lectura de la velocidad angular
Para leer la velocidad angular se conecta la salida del sensor infrarrojo reflexivo (en concreto la salida del inversor schmitt) a una entrada de interrupción externa del microcontrolador y se programa dicha interrupción externa para que se dispare en uno de los flancos (subida o bajada, pero no en ambos a la vez). De esta forma y al estar el disco pintado mitad negro y mitad blanco, cada interrupción se corresponderá con una vuelta del eje de rotación.
float RPMReader::rpm; void RPMReader::init() { DDRD &= 0xFE; // PD0 as input cli(); EICRA = (1 << ISC01) | (1 << ISC00); // external INT0 EIMSK = (1 << INT0); sei(); Chronometer::init(); Chronometer::microseconds = 0; } void RPMReader::__isr() { uint32_t delta = Chronometer::microseconds; Chronometer::microseconds = 0; if (delta > 0) rpm = (((float) 1) / delta) * 60000000; EIFR |= (1 << INTF0); } ISR(INT0_vect) { RPMReader::__isr(); }
Cada vez que se ejecuta la interrupción (da una vuelta el eje de rotación) se obtiene la cantidad de microsegundos que han pasado desde la anterior vuelta y se calcula la velocidad angular:
uint32_t delta = Chronometer::microseconds; Chronometer::microseconds = 0; if (delta > 0) rpm = (((float) 1) / delta) * 60000000;
Señal PWM de salida
La salida del controlador borroso no es en este caso directamente el valor absoluto PWM, sino el "incremento" (o una especie de derivada) de dicho valor PWM. Esto simplifica el diseño del controlador borroso pero complica la etapa de salida, ya que hay que poner un "integrador" a la salida del controlador que convierta los incrementos PWM en valores absolutos PWM.

Afortunadamente este "integrador" no es más que un acumulador en el que se van sumando, en cada iteración, los incrementos que emite el controlador borroso. Es esta suma la que se emite como PWM para accionar el motor.
SpeedDeltaFuzzyValueWriter::SpeedDeltaFuzzyValueWriter() { this->sum = 0; } void SpeedDeltaFuzzyValueWriter::setValue(float v) { this->sum += v; if (this->sum > 255) this->sum = 255; else if (this->sum < 0) this->sum = 0; uint8_t aux = (uint8_t) this->sum; PWM::setPB7Value(aux); }
Control borroso
Para realizar el controlador se plantea como variable de entrada al mismo el error de la velocidad de rotación (deseada - actual) en revoluciones por minuto (RPM) y como variable de salida, el incremento (una especie de derivada) del ciclo de trabajo de la señal PWM que alimenta al motor DC. Se definen unos sencillos conjuntos borrosos asociados a cada una de estas dos variables:
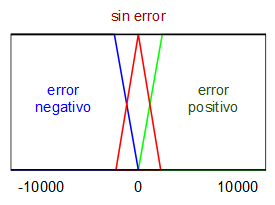
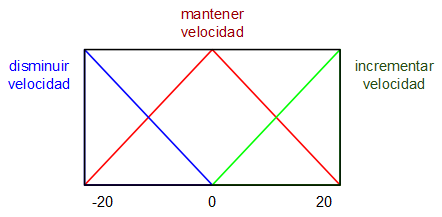
Mientras que las reglas de lógica borrosa que se van a utilizar son las siguientes:
SI (error ES error negativo) ENTONCES salida ES decrementar velocidad
SI (error ES sin error) ENTONCES salida ES mantener velocidad
SI (error ES error positivo) ENTONCES salida ES incrementar velocidad
Como puede apreciarse, las reglas son sencillas y fáciles de ajustar, de recordar y de mantener. Además, el hecho de que la variable de salida sea un incremento en lugar de un valor absoluto simplifica enormemente las reglas y los conjuntos.
Ejemplo 1
Supongamos que queremos alcanzar una velocidad de 3000 RPM y que la velocidad actual medida por el sensor de velocidad es de 2000 RPM, el error será, por tanto de 1000 RPM (consigna - valor real). Lo primero que se hace es “borrosificar” o “fuzzyficar” esta lectura:
Para la expresión “(error ES error negativo)” se calcula el grado de pertenencia de 1000 RPM al conjunto borroso “error negativo”, para la expresión “(error ES sin error)” se calcula el grado de pertenencia de 1000 RPM al conjunto borroso “sin error” y para la expresión “(error ES error positivo)” se calcula el grado de pertenencia de 1000 RPM al conjunto borroso “error positivo”:
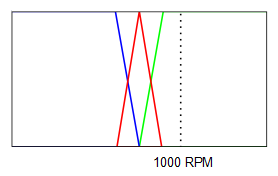
Como se puede ver:
$$\mu_{error \space negativo}(1000)=0$$
$$\mu_{sin \space error}(1000)=0$$
$$\mu_{error \space positivo}(1000)=1$$
Por lo tanto, para la salida:
$$\mu_{decrementar \space velocidad}(\Delta PWM)=0$$
$$\mu_{mantener \space velocidad}(\Delta PWM)=0$$
$$\mu_{incrementar \space velocidad}(\Delta PWM)=1$$
A continuación se calcula mediante el método de la media ponderada de centros, el valor de la salida:
$$\Delta PWM={0·C_{dec. \space velocidad}+0·C_{mant. \space velocidad}+1·C_{inc. \space velocidad} \over 0+0+1}=C_{inc. \space velocidad}=20$$
En este caso el resultado el directamente el centro del conjunto borroso “incrementar velocidad”, que vale 20, con lo que incrementamos la velocidad.
Ejemplo 2
Supongamos ahora que queremos alcanzar la misma velocidad de 3000 RPM y que la velocidad actual medida por el sensor de velocidad es de 3050 RPM, el error será, por tanto de -50 RPM (consigna - valor real). Lo primero que se hace de nuevo es “borrosificar” o “fuzzyficar” esta lectura:
Se calculan los diferentes grados de pertenencia:
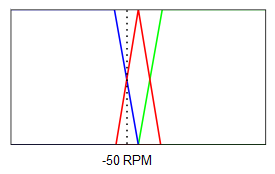
Como se puede ver:
$$\mu_{error \space negativo}(-50)=0.5$$
$$\mu_{sin \space error}(-50)=0.5$$
$$\mu_{error \space positivo}(-50)=0$$
Por lo tanto, para la salida:
$$\mu_{decrementar \space velocidad}(\Delta PWM)=0.5$$
$$\mu_{mantener \space velocidad}(\Delta PWM)=0.5$$
$$\mu_{incrementar \space velocidad}(\Delta PWM)=0$$
A continuación se calcula mediante el método de la media ponderada de centros, el valor de la salida:
$$\Delta PWM={0.5·C_{dec. \space velocidad}+0.5·C_{mant. \space velocidad}+0·C_{inc. \space velocidad} \over 0.5+0.5+0}=-10$$
Un valor de -10 en el incremento del PWM, disminuye dicho valor y, por tanto, hace que se disminuya la velocidad del motor.
En condiciones ideales, con una entrada de error de 0 RPM tendríamos:
$$\mu_{error \space negativo}(0)=0$$
$$\mu_{sin \space error}(0)=1$$
$$\mu_{error \space positivo}(0)=0$$
Por lo tanto, para la salida:
$$\mu_{decrementar \space velocidad}(\Delta PWM)=0$$
$$\mu_{mantener \space velocidad}(\Delta PWM)=1$$
$$\mu_{incrementar \space velocidad}(\Delta PWM)=0$$
Y haciendo la “desborrosificación” o “defuzzyficación” nos sale:
$$\Delta PWM={0·C_{dec. \space velocidad}+1·C_{mant. \space velocidad}+0·C_{inc. \space velocidad} \over 0+1+0}=C_{mant. \space velocidad}=0$$
Un incremento del valor PWM de 0, con lo que no cambiamos la velocidad del motor.
Para dotar al sistema de un comportamiento más estable, en los sistemas reales, suele tomarse también como entrada la derivada de la velocidad angular y establecer reglas que hagan variar el PWM en función de esta otra entrada. En este caso, por simplicidad, se ha optado por utilizar como entrada sólo la velocidad angular.
Implementación
La implementación se ha realizado en C++ y las clases definidas pueden dividirse en dos grupos: las que hacen de interfaz con hardware interno, entrada y salida (lectura del sensor de infrarrojos reflexivo para calcular la velocidad angular, salida PWM, timers, etc.) y las que forman parte del motor de inferencia borroso (expresiones, conjuntos borrosos, variables lingüísticas, reglas, etc.)
Diagrama de clases 1:
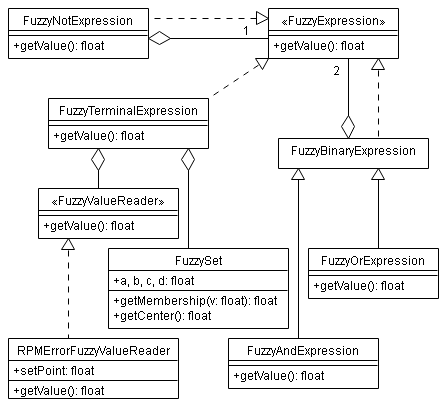
Diagrama de clases 2:
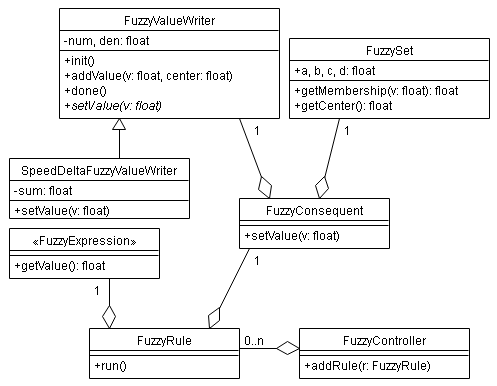
Los conjuntos borrosos (clase FuzzySet) se definen de forma trapezoidal:
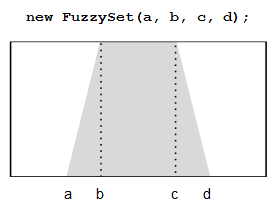
En el caso concreto que nos ocupa los conjuntos estarán, por tanto, definidos así:
FuzzySet negativeError(-10000, -10000, -100, 0); FuzzySet noError(-100, 0, 0, 100); FuzzySet positiveError(0, 100, 10000, 10000); FuzzySet decreaseSpeed(-20, -20, -20, 0); FuzzySet keepSpeed(-20, 0, 0, 20); FuzzySet increaseSpeed(0, 20, 20, 20);
Cada regla de inferencia borrosa estará definida por un antecedente (objeto de clase FuzzyExpression o derivadas) y por un consecuente (objeto de clase FuzzyConsequent).
FuzzyController c;
c.addRule(
new FuzzyTerminalExpression(entrada1, conjunto1),
new FuzzyConsequent(salida1, conjunto3)
); // SI (entrada1 ES conjunto1) ENTONCES salida1 ES conjunto3
En el antecedente podemos hacer combinaciones “Y”, “O” y “NO” utilizando las clases FuzzyAndExpression, FuzzyOrExpression y FuzzyNotExpression respectivamente.
c.addRule(
new FuzzyAndExpression(
new FuzzyTerminalExpression(entrada1, conjunto1),
new FuzzyTerminalExpression(entrada2, conjunto2)
),
new FuzzyConsequent(salida1, conjunto3)
); // SI (entrada1 ES conjunto1) Y (entrada2 ES conjunto2) ENTONCES salida1 ES conjunto3
De esta forma podemos crear reglas de inferencia borrosa tan complejas como queramos. Se ha aprovechado, además, la capacidad que tiene C++ de redefinir operadores y se han usado los operadores “&&”, “||”, “!” y “%” como sinónimos de FuzzyAndExpression, FuzzyOrExpression, FuzzyNotExpression y FuzzyTerminalExpression, respectivamente:
FuzzyExpression &avelino::operator % (FuzzyValueReader &vr, FuzzySet &fs) { FuzzyExpression *ret = FuzzyTerminalExpression::getInstance(vr, fs); return *ret; } FuzzyExpression &avelino::operator && (FuzzyExpression &e1, FuzzyExpression &e2) { FuzzyExpression *ret = FuzzyAndExpression::getInstance(e1, e2); return *ret; } FuzzyExpression &avelino::operator || (FuzzyExpression &e1, FuzzyExpression &e2) { FuzzyExpression *ret = FuzzyOrExpression::getInstance(e1, e2); return *ret; } FuzzyExpression &avelino::operator ! (FuzzyExpression &e) { FuzzyExpression *ret = FuzzyNotExpression::getInstance(e); return *ret; }
Ahora se puede escribir la regla de ejemplo de antes “SI (entrada1 ES conjunto1) Y (entrada2 ES conjunto2) ENTONCES salida 1 ES conjunto3” de la siguiente manera:
c.addRule(
(entrada1 % conjunto1) && (entrada2 % conjunto2),
new FuzzyConsequent(salida1, conjunto3)
);
Como se puede apreciar, la sintaxis se vuelve más clara y las reglas son más fáciles de leer y de mantener. En el caso que nos ocupa las reglas se definen de la siguiente manera:
c.addRule(
rpmError % negativeError,
new FuzzyConsequent(speedDelta, decreaseSpeed)
);
c.addRule(
rpmError % noError,
new FuzzyConsequent(speedDelta, keepSpeed)
);
c.addRule(
rpmError % positiveError,
new FuzzyConsequent(speedDelta, increaseSpeed)
);
Finalmente, en el bucle principal de la aplicación lo único que se hace es iterar el motor de inferencia borroso (FuzzyController::run) cada 200 milisegundos:
DDRC |= 0x80; while (true) { if (Chronometer::microseconds2 > 200000) { // each 200ms Chronometer::microseconds2 = 0; c.run(); } // turn on led when set point reached if ((RPMReader::rpm >= SET_POINT_LOW) && (RPMReader::rpm <= SET_POINT_HIGH)) PORTC |= 0x80; else PORTC &= 0x7F; }

Todo el código fuente puede descargarse de la sección soft.
[ 2 comentarios ] ( 12056 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 5445 )
( 3 / 5445 )
 Calendario
Calendario




