Plano z
La herramienta fundamental para el cálculo de filtros digitales es la transformada Z y su plano complejo asociado, denominado "plano z". Se asume que el lector está medianamente familiarizado con la transformada z y no se abordarán los detalles ni las propiedades de la misma.
La transformada z transforma una función, situada en el dominio discreto del tiempo $x[n]$, en otra función, situada en el dominio complejo de z $X(z)$. Esta transformación es equivalente a la transformada de Laplace en el dominio continuo y tiene ambas propiedades similares en cuanto a linealidad y estabilidad. Al igual que la transformada de Laplace, la transformada Z también se utiliza para modelar funciones de transferencia de sistemas, en el caso de la transformada Z, son sistemas discretos.
Es decir, si para un filtro analógico tenemos una función de transferencia $H(s)$, caracterizada principalmente por sus ceros y sus polos, para un filtro digital tendremos también una función de transferencia $H(z)$, caracterizada también por sus ceros y sus polos. Tanto en el caso de Laplace como en el caso Z los ceros determinan para qué tipo de señales el filtro "tiende a cancelar la entrada" y los polos determinan para qué tipo de señales el filtro "tiende a amplificar la entrada" o incluso entrar en resonancia. La regla básica que debe cumplirse en un filtro analógico es que los polos de $H(s)$ nunca deben tener parte real positiva (deben estar siempre localizados en el semiplano izquierdo del plano complejo $s$), mientras que en caso de un filtro digital, los polos de $H(z)$ nunca deben alojarse fuera de la circunferencia unitaria centrada en el origen del plano complejo $z$ (es decir, los polos en un filtro digital deben cumplir que $|z| < 1$).
Diseño de un filtro resonante sencillo
En el plano z no se mapean frecuencias absolutas como en el plano s, sino que se mapean frecuencias "relativas" a la frecuencia de muestreo y a lo largo de la longitud de la circunferencia de radio 1. La frecuencia asociada a un valor complejo del plano z se corresponde con el ángulo (argumento) de dicho valor: un ángulo de 0 radianes se corresponde con un valor en continua (0 Hz) mientras que un valor de $\pi$ radianes se corresponde con la mitad de la frecuencia de muestreo (frecuencia Nyquist). Si, por ejemplo, muestreamos a 44100 Hz, la frecuencia máxima ($\pi$) será de 22050 Hz, mientras que si muestreamos a 8000 Hz la misma frecuencia PI se corresponderá con 4000 Hz.
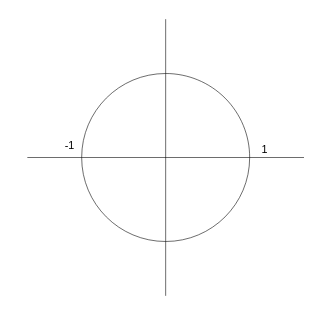
El diseño básico de filtros digitales es muy sencillo y se resume en cuatro reglas principales:
- Alojar tantos ceros sobre la circunferencia de radio 1 como frecuencias queramos cancelar. Lo importante de cada cero será su ángulo (= frecuencia) con respecto al origen. Por ejemplo si colocamos un cero en en punto $z = 1$, que se corresponde con un ángulo de 0 radianes, nuestro filtro eliminará la componente de continua de la señal.
- Alojar tantos polos DENTRO de la circunferencia de radio 1 ($|z| < 1$) como frecuencias queramos amplificar. En este caso es importante tanto el ángulo (= frecuencia que queremos reforzar) como su magnitud o módulo (= nivel de refuerzo). Si hacemos que la magnitud (el módulo) de un polo sea 1 ($|z| = 1$) el filtro auto-oscilará a esa frecuencia. Por ejemplo, si colocamos un polo en $z = -1$, que se corresponde con un ángulo $\pi$, estaremos reforzando las señales con frecuencia próxima a $\pi$ (= la mitad de la frecuencia de muestreo).
- Los polos y ceros que tengan parte imaginaria diferente de 0 deberán ponerse por pares conjugados para poder trabajar con señales reales (sin componente imaginaria). Por ejemplo, si estamos muestreando a 44100 Hz y queremos cancelar las frecuencias próximas a 11025 Hz (frecuencia ${\pi \over 2}$), debemos colocar DOS polos conjugados: uno en $(0, 1)$, formando un ángulo de 90 grados (${\pi \over 2}$) y otro en $(0, -1)$ (su conjugado).
- Al final lo habitual es también ajustar la ganancia global del filtro (aunque en este caso no lo hemos hecho por simplicidad). Esto se hace habitualmente debido a que a veces los polos meten mucha ganancia en la banda de paso y es necesario escalar la salida antes de emitirla o la entrada antes de procesarla.
Si, por ejemplo, queremos hacer un filtro paso bajo, lo habitual, es poner un cero en $z = -1$ (sobre la circunferencia de radio 1 con ángulo $\pi$) con el objetivo de anular las altas frecuencias y un polo (con su complejo conjugado) cerca de la frecuencia de corte de nuestro filtro. En nuestro caso de estudio, se trata de un filtro resonante sencillo, por lo que definiremos dos ceros: uno en $z = 1$ (0 radianes), y otro en $z = -1$, ($\pi$ radianes). Como queremos una única frecuencia de resonancia, definimos un único polo (junto con su complejo conjugado, por lo que realmente serán dos polos).
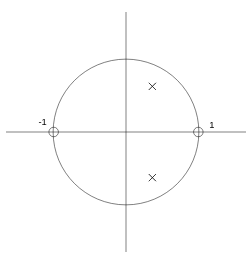
Con esta configuración de dos ceros reales en -1 y 1 y dos polos complejos conjugados en la frecuencia de resonancia tenemos la siguiente función de transferencia en Z:
$$H(z) = {(z + 1)(z - 1) \over (z - p_1)(z - p_1^\prime)}$$
Para la que se cumple que:
$$p_1 = a + bi \;\;\;\;\;\;\;\;\; p_1^\prime = a - bi$$
Desarrollando el denominador (los polos) de $H(z)$ tenemos que:
$$(z - p_1)(z - p_1^\prime) = z(z - p_1^\prime) - p_1(z - p_1^\prime)$$
$$ = z^2 - zp_1^\prime -p_1z + p_1p_1^\prime$$
$$ = z^2 - z(p_1^\prime + p_1) + p_1p_1^\prime$$
$$ = z^2 - z2a + p_1p_1^\prime$$
$$ = z^2 - z2a + a^2 + b^2$$
Nótese que, al ser los polos complejos conjugados, las operaciones
$(p_1^\prime + p_1)$ y $p_1p_1^\prime$ dan como resultado, valores reales (sin componente imaginaria). Por otro lado, si desarrollamos el numerador (los ceros) de $H(z)$ tenemos que:
$$(z + 1)(z - 1) = z(z - 1) + (z - 1)$$
$$ = z^2 - z + z - 1$$
$$ = z^2 - 1$$
Por tanto la función de transferencia $H(z)$ puede reescribirse de la siguiente manera:
$$H(z) = {{z^2 - 1} \over {z^2 - z2a + a^2 + b^2}}$$
Podemos visualizar la respuesta en frecuencia de este sistema asignando a z diferentes valores sobre la circunferencia unitaria $z = e^{iw} = cos(w) + i sen(w)$:
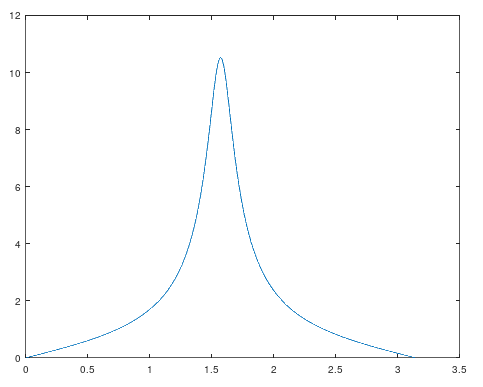
Para generar esta gráfica se ejecutó el siguiente código octave que sitúa el polo (= la frecuencia de resonancia del filtro) en ${\pi \over 2}$:
m = 0.9; w = pi / 2; a = m * cos(w); b = m * sin(w); # respuesta en frecuencia TAM = 1000; responseX = zeros(1, TAM); responseY = zeros(1, TAM); for n = 1:TAM w = (n / TAM) * pi; responseX(n) = w; z = cos(w) + (i * sin(w)); responseY(n) = abs(((z * z) - 1) / ((z * z) - (z * 2 * a) + (a * a) + (b * b))); endfor plot(responseX, responseY);
Implementación del filtro
Ahora que ya tenemos la función de transferencia en el dominio Z del filtro que queremos, el siguiente paso es pasar al dominio discreto y calcular los coeficientes en diferencias finitas para poder implementarlo. Lo primero que se hace es evitar que haya exponentes mayores que 0 para z (exponentes positivos de z se corresponden a muestras "futuras" en el tiempo). Esto se soluciona de forma muy sencilla multiplicando numerador y denominador de $H(z)$ por $z^{-2}$, esto mantiene $H(z)$ igual pero elimina los exponentes positivos:
$$H(z) = {{z^2 - 1} \over {z^2 - z2a + a^2 + b^2}}$$
$$H(z) = {{z^{-2}(z^2 - 1)} \over {z^{-2}(z^2 - z2a + a^2 + b^2)}}$$
$$H(z) = {{1 - z^{-2}} \over {1 - z^{-1}2a + z^{-2}(a^2 + b^2)}}$$
Ahora ya podemos calcular los coeficientes de forma más sencilla. Como $H(z)$ es una función de transferencia en Z tenemos que, si $X(z)$ es la transformada Z de la entrada e $Y(z)$ es la transformada Z de la salida, entonces:
$$Y(z) = H(z) X(z) = {{1 - z^{-2}} \over {1 - z^{-1}2a + z^{-2}(a^2 + b^2)}} X(z)$$
Y, por tanto:
$$Y(z)(1 - z^{-1}2a + z^{-2}(a^2 + b^2)) = X(z)(1 - z^{-2})$$
$$Y(z)-Y(z)z^{-1}2a+Y(z)z^{-2}(a^2 + b^2) = X(z) - X(z)z^{-2}$$
Como la transformada Z es lineal y se cumple que la transformada Z de un valor desplazado k muestras en el tiempo es la siguiente:
$$Z \left\{ x[n - k] \right\} = X(z)z^{-k}$$
Entonces podemos hacer la antitransformada Z de forma sencilla:
$$y[n] - y[n - 1]2a + y[n - 2](a^2 + b^2) = x[n] - x[n - 2]$$
Y, despejando $y[n]$ tenemos que:
$$y[n] = x[n] - x[n - 2] + y[n - 1]2a - y[n - 2](a^2 + b^2)$$
Esto, como se puede ver, es una ecuación en diferencias finitas, que es muy fácil de implementar tanto en hardware como en software. Veamos una ejemplo de código octave que genera ruido blanco y luego lo hace pasar por el filtro (aplica la ecuación en diferencias finitas con los mismos valores a y b, esto es, misma frecuencia de resonancia en ${\pi \over 2}$).
m = 0.9; w = pi / 2; a = m * cos(w); b = m * sin(w); TAM = 1000; input = (rand(1, N) .* 2) .- 1; # TAM valores aleatorios entre -1 y 1 ym1 = 0; ym2 = 0; xm1 = 0; xm2 = 0; output = zeros(1, TAM); for n = 1:TAM output(n) = input(n) - xm2 + (ym1 * 2 * a) - (ym2 * ((a * a) + (b * b))); ym2 = ym1; ym1 = output(n); xm2 = xm1; xm1 = input(n); endfor subplot(2, 2, 1) plot(input); title('Ruido'); subplot(2, 2, 2) plot(output); title('Ruido filtrado'); subplot(2, 2, 3) plot(abs(fft(input)(1:(N / 2)))); title('Espectro del ruido'); subplot(2, 2, 4) plot(abs(fft(output)(1:(N / 2)))); title('Espectro del ruido filtrado');
A continuación se pueden ver las señales y los espectros en frecuencia de las mismas y se puede comprobar como el funcionamiento del filtro es el esperado:
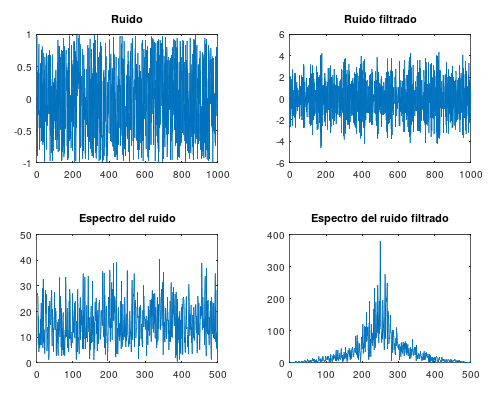
[ añadir comentario ] ( 2788 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 2753 )
( 3 / 2753 )Partiendo del montaje realizado en el post anterior, se han realizado varias modificaciones y mejoras. El parser MIDI de esta segunda iteración genera ahora 3 señales de control, de 7 bits cada una, que se utilizan para controlar la frecuencia de corte, la resonancia y la ganancia de la entrada de un filtro paso bajo de segundo orden:
Este sería el diagrama de bloques de esta segunda iteración:
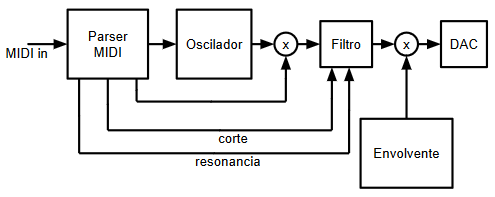
Parser MIDI mejorado
En la versión iniciar el parser MIDI no se tuvieron en cuenta algunas características "raras" que se dan el algunos teclados controladores y al mismo tiempo se asumía que un "note off" posterior a un "note on" siempre era de la misma tecla, lo cual es demasiado suponer, sobre todo cuando quien toca es un humano. Cuando un humano toca una secuencia de notas en un teclado (por ejemplo: La, Mi, Do) uno puede pensar que los mensaje que manda el teclado controlador son los siguientes:
noteOn(La), noteOff(La), noteOn(Mi), noteOff(Mi), noteOn(Do), noteOff(Do)
Sin embargo lo cierto es que a veces un humano pulsa la siguiente tecla al mismo tiempo o antes de soltar la anterior:
noteOn(La), noteOn(Mi), noteOff(La), noteOff(Mi), noteOn(Do), noteOff(Do)
Con la anterior versión del parser, que asumía que un noteOff se correspondía siempre con el noteOn inmediatamente anterior, lo que ocurría era que cuando al sinte le llegaba el noteOff(La) callaba la nota Mi disparada justo antes porque asumía que ese noteOff se correspondía con dicha nota Mi. En la nueva versión del parse este noteOff(Mi) es ignorado por la máquina de estados por lo que la respuesta del sintetizador es más natural.
Para mejorar el comportamiento y la funcionalidad del parser MIDI se ha optado por un diseño basado en máquinas de estado en serie y en paralelo en lugar de una única máquina de estados grande. El parser MIDI se ha divido en dos etapas (Stage1 y Stage2), la primera etapa genera señales "KeyOn" y "KeyOff" limpias por cables separados y además implementa en paralelo una máquina de estados aparte para procesar los mensajes de "Control Change". En la segunda etapa se implementa la lógica anteriormente descrita de ignorar los "Note Off" que no se corresponden con el mensaje "Note On" inmediatamente anterior.
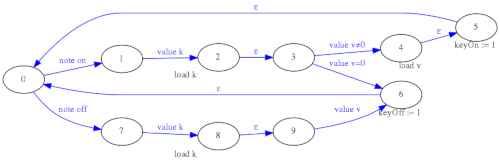
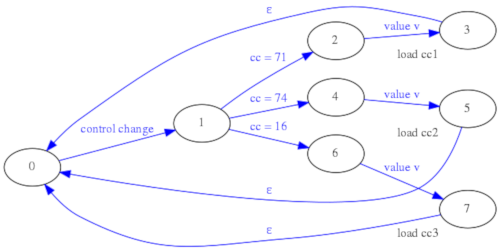
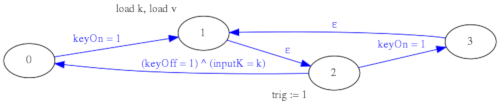
De esta forma, aunque aparentemente se ha complicado el diseño, se han separado los problemas y es más sencillo introducir modificaciones y depurar errores en las máquinas de estado. Cada una por separado es más sencilla y fácil de trazar que una hipotética máquina de estados única para todo.
Además de la mejora en el procesado de los mensajes "Note On" y "Note Off", este parser ya reconoce mensajes de tipo "Control Change", en concreto para tres valores prefijados de controlador: 71, 74 y 16, que se asignarán en el sintetizador a la frecuencia de corte del filtro, la resonancia del filtro y la ganancia de entrada del filtro.
Filtro paso bajo de segundo orden
Se ha optado por la implementación estándar de un filtro de estado variable (state variable filter). Se trata de un filtro de segundo orden (dos polos) que genera simultáneamente 3 salidas:
- paso bajo (con pendiente de filtrado de 12 dB/octava)
- paso alto (con pendiente de filtrado de 12 dB/octava)
- paso banda (con pendiente de filtrado de 6 dB/octava)
No son grandes pendientes de filtrado pero siempre se pueden mejorar poniendo varios filtros en cascada. La implementación que se ha utilizado es la descrita en el libro "Musical Applications of Microprocessors" de Hal Chamberlin (dicha implementación ya fue usada sobre un microcontrolador en este post). El filtro de estado variable viene determinado por el siguiente sistema de ecuaciones en diferencias finitas:
$$pasoAlto[n] = entrada - ({r \times pasoBanda[n-1]}) - pasoBajo[n]$$
$$pasoBanda[n] = ({f \times pasoAlto[n]}) + pasoBanda[n - 1]$$
$$pasoBajo[n] = ({f \times pasoBanda[n - 1]}) + pasoBajo[n - 1]$$
Siendo:
$$f = 2\sin\left({\pi F_c \over F_s}\right)$$
$$r = {1 \over Q}$$
Siendo $F_c$ la frecuencia de corte del filtro, $F_s$ la frecuencia de muestreo y $Q$ la Q del filtro (la resonancia).
Si se reordenan las ecuaciones en diferencias:
$$pasoBajo[n] = ({f \times pasoBanda[n - 1]}) + pasoBajo[n - 1]$$
$$pasoAlto[n] = entrada - ({r \times pasoBanda[n - 1]}) - pasoBajo[n]$$
$$pasoBanda[n] = ({f \times pasoAlto[n]}) + pasoBanda[n - 1]$$
Podemos olvidarnos de los índices:
pasoBajo += f * pasoBanda
pasoAlto = entrada - (r * pasoBanda) - pasoBajo
pasoBanda += f * pasoAlto
Como se puede apreciar es preciso mantener en memoria (registro) al menos las variables pasoBajo y pasoBanda entre que se procesa una muestra y la siguiente (se trata de un filtro digital de segundo orden).
Para implementar dicho filtro sobre FPGA lo que necesitaremos serán básicamente los siguientes elementos:
- Al menos tres registros en los que almacenaremos los valores "pasoBajo", "pasoBanda" y "pasoAlto" (aunque realmente podríamos no gastar un registro para "pasoAlto", lo vamos a incluir para poder disponer de esa salida en el módulo).
- Una unidad de suma con multiplicación: Un módulo combinacional que realiza la operación: A = (B * C) + D (en muchos casos D = A, por lo que se puede ver como A += B * C)
- Una máquina de estados para controlar qué operandos y operaciones se hacen en cada momento.
Con estos elemento y teniendo en cuenta las ecuaciones anteriores, podemos hacer una propuesta de secuenciación de operaciones como sigue:
1. LP := (cutoff * BP) + LP
2. HP := (0 * x ) + IN
3. HP := (-reso * BP) + HP
4. HP := (-1 * LP) + HP
5. BP := (cutoff * HP) + BP
Cada paso requiere un único ciclo de reloj por lo que bastará con implementar una máquina de estados que, por cada muestra que llegue, pase por los 5 estados de forma secuencial para que los registros LP, BP y HP (LowPass, BandPass y HighPass) tengan los valores de salida del filtro que necesitamos. Nótese que será preciso utilizar aritmética de punto fijo y en nuestro caso se ha optado por un formato Q16.16 (16 bits de parte entera y 16 bits de parte fraccionaria).
A continuación puede verse como quedaría la implementación del filtro en VHDL:
library ieee; use ieee.std_logic_1164.all; use ieee.numeric_std.all; entity StateVariableFilter is port ( Reset : in std_logic; Clk : in std_logic; EnableIn : in std_logic; SampleIn : in std_logic_vector(15 downto 0); CutOffIn : in std_logic_vector(31 downto 0); -- 0..1 fixed point Q16.16 ResonanceIn : in std_logic_vector(31 downto 0); -- 0..1 fixed point Q16.16 SampleOut : out std_logic_vector(15 downto 0); EnableOut : out std_logic ); end entity; architecture RTL of StateVariableFilter is signal LPDBus : std_logic_vector(31 downto 0); signal LPQBus : std_logic_vector(31 downto 0); signal HPDBus : std_logic_vector(31 downto 0); signal HPQBus : std_logic_vector(31 downto 0); signal BPDBus : std_logic_vector(31 downto 0); signal BPQBus : std_logic_vector(31 downto 0); signal MultOperandA : std_logic_vector(31 downto 0); signal MultOperandB : std_logic_vector(31 downto 0); signal MultResult64 : std_logic_vector(63 downto 0); signal MultResult : std_logic_vector(31 downto 0); signal AddOperandB : std_logic_vector(31 downto 0); signal AddResult : std_logic_vector(31 downto 0); signal NegResonance : std_logic_vector(31 downto 0); signal FSMDBus : std_logic_vector(2 downto 0); signal FSMQBus : std_logic_vector(2 downto 0); begin process (Clk) begin if (Clk'event and (Clk = '1')) then LPQBus <= LPDBus; end if; end process; process (Clk) begin if (Clk'event and (Clk = '1')) then HPQBus <= HPDBus; end if; end process; process (Clk) begin if (Clk'event and (Clk = '1')) then BPQBus <= BPDBus; end if; end process; process (Clk) begin if (Clk'event and (Clk = '1')) then FSMQBus <= FSMDBus; end if; end process; NegResonance <= std_logic_vector(to_signed(-to_integer(signed(ResonanceIn)), 32)); MultOperandA <= CutOffIn when ((FSMQBus = "001") or (FSMQBus = "101")) else NegResonance when (FSMQBus = "011") else std_logic_vector(to_signed(-65536, 32)) when (FSMQBus = "100") else -- -65536 es -1 en notación Q16.16 std_logic_vector(to_signed(0, 32)); MultOperandB <= LPQBus when (FSMQBus = "100") else BPQBus when ((FSMQBus = "001") or (FSMQBus = "011")) else HPQBus; AddOperandB <= LPQBus when (FSMQBus = "001") else BPQBus when (FSMQBus = "101") else HPQBus when ((FSMQBus = "011") or (FSMQBus = "100")) else std_logic_vector(to_signed(to_integer(signed(SampleIn)), 32)); --MultResult64 <= std_logic_vector(to_signed(to_integer(signed(MultOperandA)) * to_integer(signed(MultOperandB)), 64)); MultResult64 <= std_logic_vector(signed(MultOperandA) * signed(MultOperandB)); MultResult <= MultResult64(47 downto 16); --AddResult <= std_logic_vector(to_signed(to_integer(signed(MultResult)) + to_integer(signed(AddOperandB)), 32)); AddResult <= std_logic_vector(signed(MultResult) + signed(AddOperandB)); LPDBus <= std_logic_vector(to_signed(0, 32)) when (Reset = '1') else AddResult when (FSMQBus = "001") else LPQBus; HPDBus <= std_logic_vector(to_signed(0, 32)) when (Reset = '1') else AddResult when ((FSMQBus = "011") or (FSMQBus = "100") or (FSMQBus = "010")) else HPQBus; BPDBus <= std_logic_vector(to_signed(0, 32)) when (Reset = '1') else AddResult when (FSMQBus = "101") else BPQBus; -- fsm -- LP += cutoff * BP -- HP = in - (resonance * BP) - LP -- BP += cutoff * HP FSMDBus <= "000" when ((Reset = '1') or (FSMQBus = "110")) else -- MultOperandA MultOperandB AddOperandB "001" when ((FSMQBus = "000") and (EnableIn = '1')) else -- LP := cutoff * BP + LP "010" when (FSMQBus = "001") else -- HP := 0 * x + IN "011" when (FSMQBus = "010") else -- HP := -reso * BP + HP "100" when (FSMQBus = "011") else -- HP := -1 * LP + HP "101" when (FSMQBus = "100") else -- BP := cutoff * HP + BP "110" when (FSMQBus = "101") else "000"; EnableOut <= '1' when (FSMQBus = "110") else '0'; SampleOut <= std_logic_vector(to_signed(-32768, 16)) when (to_integer(signed(LPQBus)) < -32768) else std_logic_vector(to_signed(32767, 16)) when (to_integer(signed(LPQBus)) > 32767) else LPQBus(15 downto 0); end architecture;
La máquina de estados espera hasta que la entrada "EnableIn" se ponga a "1", dicho evento es la señal que indica al filtro que debe realizar una iteración (i.e. calcular la siguiente muestra a partir de la entrada "SampleIn").
Todo el código está disponible en la sección soft.
[ 1 comentario ] ( 2296 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 4618 )
( 3 / 4618 )Tradicionalmente, la síntesis y el procesado de sonido digital siempre se ha delegado a nivel hardware en el uso de DSPs. El uso de FPGAs para sustituir DSPs es una tendencia actual derivada del abaratamiento de las FPGAs y de la incursión de las mismas dentro del mundo de la electrónica amateur y DIY. Actualmente una FPGA media tiene suficiente potencia para llevar a cabo múltiples operaciones DSP a una velocidad incluso mayor. El problema con las FPGAs es la forma de programarlas, que requiere un pensamiento abstracto de tipo diferente al razonamiento algorítmico tradicional que se utiliza para programar CPUs y DSPs estándar. Este post se introducirá en el diseño y la implementación de un sintetizador monofónico muy simple sobre una FPGA.
La idea
La idea de esta primera versión es implementar un sintetizador monofónico con un único oscilador de diente de sierra, que sólo lea mensajes de tipo NoteOn y NoteOff y que reproduzca el sonido a través de un DAC I2S.
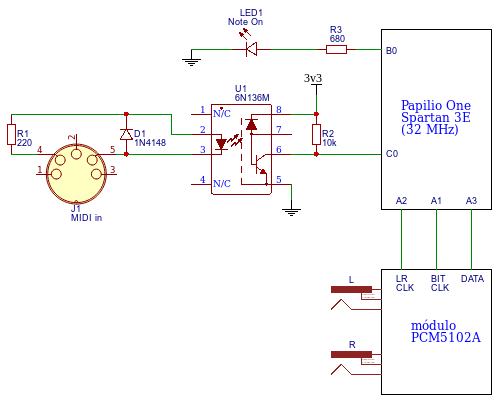
Como se puede apreciar se trata del típico circuito de entrada MIDI con optoacoplador más un PCM5102A como DAC I2S de alta calidad. Los mensajes MIDI de NoteOn se traducen en tonos que genera el oscilador.
El interfaz de salida I2S para el DAC externo
El protocolo I2S es un estándar definido para transportar sonido digital a muy cortas distancias (dentro de una misma placa, por ejemplo). Es estándar de facto en casi la totalidad de los conversores DAC y ADC de alta calidad del mercado de todos los fabricantes y se trata de un protocolo relativamente ligero y fácil de implementar.
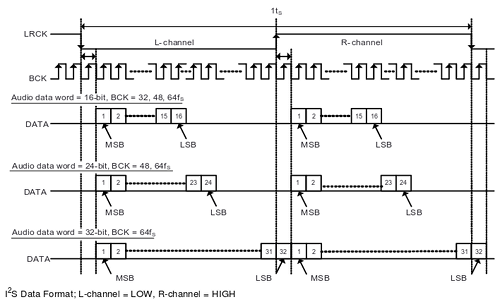
(imagen © Texas Instruments Incorporated, extraida con permiso de la hoja de datos del PCM5102A)
Existe una variante del I2S denominada "Left Justified" que simplifica el uso del reloj LR, evitando el desfase de un bit entre el envío de cada palabra para el canal izquierdo y el canal derecho:
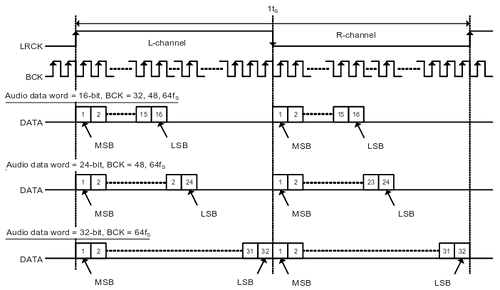
(imagen © Texas Instruments Incorporated, extraida con permiso de la hoja de datos del PCM5102A)
Y que es la variante I2S que se ha usado en este proyecto ya que es más fácil de implementar que el estándar original y actualmente todos los DACs del mercado la soportan. A continuación puede verse lo que sería el diagrama de bloques de la interfaz I2S-LJ dentro de la FPGA:
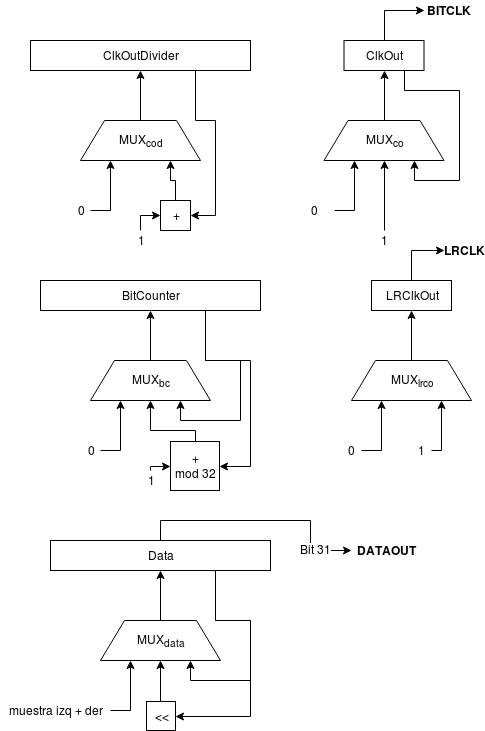
Las diferentes tablas de verdad de cada uno de los bloques combinacionales serían las siguientes:
| Entradas | Salidas | |
|---|---|---|
| ClkOutDivider == 22 | Reset | MUXcod |
| 0 | 0 | + |
| 0 | 1 | 0 |
| 1 | X | 0 |
| Entradas | Salidas | ||
|---|---|---|---|
| ClkOutDivider == 22 | ClkOutDivider == 10 | Reset | MUXco |
| 1 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| en otro caso | ClkOut | ||
| Entradas | Salidas | |
|---|---|---|
| ClkOutDivider == 22 | Reset | MUXbc |
| X | 1 | 0 |
| 1 | 0 | + mod 32 |
| en otro caso | BitCounter | |
| Entradas | Salidas | |
|---|---|---|
| BitCounter < 16 | Reset | MUXlrco |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | X | 1 |
| Entradas | Salidas | |
|---|---|---|
| ClkOutDivider == 22 | BitCounter == 31 | MUXdata |
| 0 | X | data |
| 1 | 0 | << |
| 1 | 1 | muestra izq + der |
Como se puede apreciar el mecanismo se basa en meter en un registro de desplazamiento de 32 bits las dos palabras de 16 bits de cada canal (izquierdo + derecho) e ir emitiendo bit a bit ese registro cambiando la polaridad de la señal LRCLK cada 16 bits para indicar canal izquierdo o canal derecho.
El oscilador
El oscilador se ha implementado como un sencillo acumulador de fase.
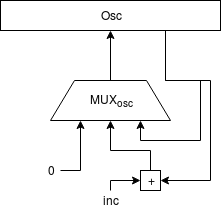
Como lo que se busca es un oscilador de diente de sierra, lo más sencillo es aprovechar el comportamiento natural de cualquier acumulador que, cuando se desborda "da la vuelta". Esto simplifica enormemente todo el diseño ya que, de forma natural, la señal resultante tiene forma de diente de sierra.
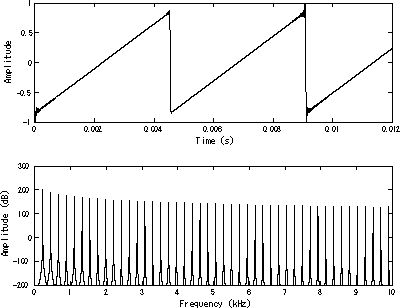
(imagen de dominio público extraida de Wikipedia)
Por cada nueva muestra que debe ser calculada, el acumulador es incrementado en una cantidad determinada, lo que provoca que su valor crezca de forma lineal (la rampa del diente de sierra). Al cabo de una cantidad suficiente de muestras, el acumulador se desbordará y "dará la vuelta" empezando de nuevo desde abajo (el "pico" del diente de sierra).
La cantidad que se use para ir incrementando el acumulador de fase determinará la frecuencia de la señal del oscilador:
$$DivisorFrecuenciaRelojI2S = {{32000000 Hz \over 44100 Hz} \over 32 bits}$$
$$inc = {{f \times 65536} \over {{32000000Hz \over DivisorFrecuenciaRelojI2S} \over 32 bits}} \times 65536$$
El incremento (inc) debe estar en formato Q16.16 (punto fijo de 16 bits de parte entera y 16 bits de parte fraccionaria), que es el formato usado por el acumulador de fase del oscilador.
Nótese que el oscilador no se incrementa en cada ciclo de reloj de la FPGA, sino cada vez que se requiere una nueva muestra por parte de la interfaz I2S-LJ para emitirla al DAC.
El parser MIDI
El módulo de procesamiento MIDI se encarga de implementar un receptor UART sencillo a 31250 baudios y una máquina de estados que vaya leyendos los datos MIDI de entrada y determinando en cada momento si hay que reproducir una nota en el oscilador (y con qué frecuencia) o no.
La UART se implementa de forma muy sencilla usando un registro de desplazamiento y un contador para medir el tiempo equivalente a 1.5 bits y a 1 bit.
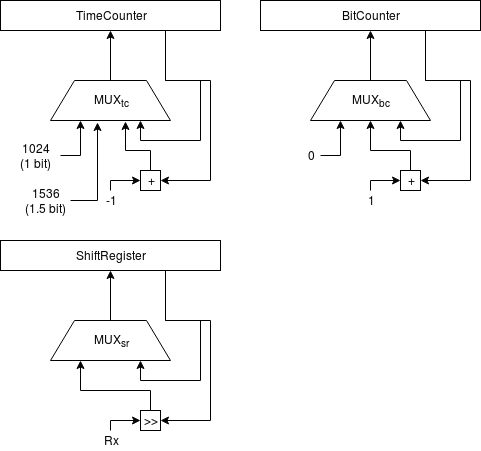
Y usando la siguiente máquina de estados:
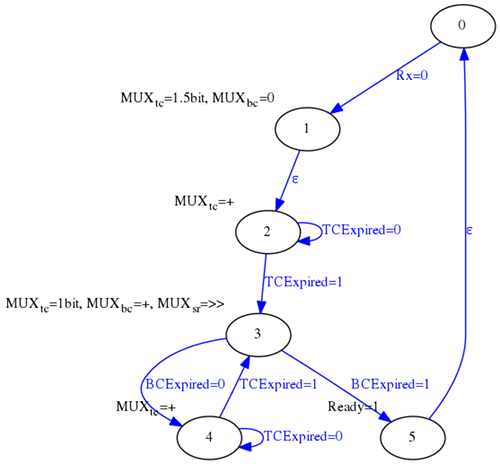
En una entrada anterior de este blog se abordó este proyecto de forma separada. Lo que se ha hecho en este caso ha sido simplificar aquel esquema para que cupiese todo dentro de un único fichero VHDL.
Una vez implementado el receptor UART, el parser MIDI se puede implementar mediante una sencilla máquina de estados que sólo detecte eventos NoteOn y NoteOff.
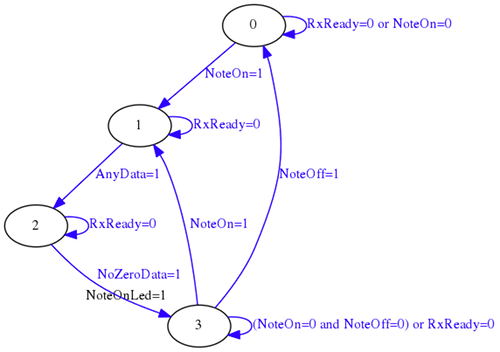
El parser MIDI en este caso no sólo determina qué nota debe ser reproducida, sino que usando una ROM interna, determina el valor de incremento que debe ser usado por el módulo oscilador para generar el tono correspondiente.
library ieee; use ieee.std_logic_1164.all; use ieee.numeric_std.all; entity NotesRom is port ( AddressIn : in std_logic_vector(6 downto 0); DataOut : out std_logic_vector(31 downto 0) ); end entity; architecture RTL of NotesRom is type RomType is array (0 to 127) of std_logic_vector(31 downto 0); constant Data : RomType := ( x"00000000", -- note 0 x"000cdf51", -- note 1 x"000da345", -- note 2 x"000e72df", -- note 3 x"000f4ed1", -- note 4 x"001037d7", -- note 5 x"00112eb9", -- note 6 x"00123449", -- note 7 x"00134966", -- note 8 x"00146efe", -- note 9 x"0015a60b", -- note 10 x"0016ef97", -- note 11 . . . . . . . . . x"368d1251", -- note 122 x"39cb7a59", -- note 123 x"3d3b4348", -- note 124 x"40df5cc9", -- note 125 x"44bae33a", -- note 126 x"48d12253" -- note 127 ); begin DataOut <= Data(to_integer(unsigned(AddressIn))); end architecture;
Para generar este conjunto de valores se hizo un pequeño programa en C++ que convirtió el valor de cada nota MIDI en el valor de incremento correspondiente para que el oscilador emita a esa frecuencia:
#include <iostream> #include <iomanip> #include <stdint.h> #include <math.h> using namespace std; double getFreq(uint8_t midiNote) { const double A4_FREQ = 440; const int32_t A4_MIDI_NOTE = 69; return A4_FREQ * pow(2.0, ((double) (((int32_t) midiNote) - A4_MIDI_NOTE)) / 12.0); } uint32_t getInc(uint8_t midiNote) { const uint32_t CLK_FREQ = 32000000; const uint32_t SAMPLE_RATE = 44100; double freq = getFreq(midiNote); double div = (((double) CLK_FREQ) / SAMPLE_RATE) / 32; double inc = (freq * 65536) / ((CLK_FREQ / div) / 32); uint32_t ret = round(inc * 65536); return ret; } int main() { for (uint8_t n = 0; n < 128; n++) cout << "\t\tx\"" << hex << setw(8) << setfill('0') << getInc(n) << "\", -- note " << dec << setw(0) << setfill(' ') << ((int) n) << endl; return 0; }
Compilando este programa y ejecutándolo, genera en la salida estándar los valores de incremento de todas las 127 notas MIDI posibles:
g++ -c -o notes_rom_generator.o notes_rom_generator.cc
g++ -o notes_rom_generator notes_rom_generator.o
./notes_rom_generator
Todo junto
A la hora de ponerlo todo junto, basta con interconectar los tres bloques:
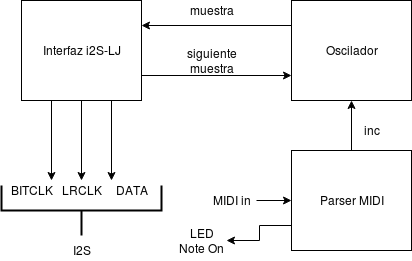
Implementación sobre cualquier FPGA
La implementación se ha desarrollado sobre una Spartan3E de Xilinx a 32 MHz pero el proyecto se puede meter en cualquier FPGA siempre y cuando se ajusten las ecuaciones y las constantes para tener en cuenta las diferentes frecuencias de reloj. En caso de que queramos meter el sintetizador en una FPGA que vaya a otra frecuencia de reloj habría que realizar los siguientes cambios:
1. Las constantes CLK_OUT_DIV y CLK_OUT_DIV_BITS de LJI2SOutput.vhd deben se recalculadas.
2. Las constantes TIME_COUNTER_BITS, TIME_COUNTER_1BIT y TIME_COUNTER_1_5BIT de UartRx.vhd deben ser recalculadas.
3. La constante CLK_FREQ dentro de notes_rom_generator.cc debe ser cambiada, hay que recompilar el programa y colocar la salida generada como los nuevos valores de NotesRom.vhd.
Todo el código fuente puede descargarse de la sección soft.
[ añadir comentario ] ( 3524 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 4756 )
( 3 / 4756 )El efecto "shuffle" o "swing" es un efecto muy utilizado en producción musical para humanizar y meter mas "groove" a canciones reproducidas por un secuenciador. El efecto consiste básicamente en adelantar o atrasar el disparo de determinadas notas durante algunos milisegundos para dar sensación de "humanidad" a la cadencia de la música. A lo largo de este post se abordará la implementación en C++ sobre Arduino de un "shuffler" MIDI para secuencias 4/4.
La forma más estándar de "shuffle" en secuencias musicales de 4/4 es la que consiste en retrasar una cantidad de tiempo determinada (milisegundos) la segunda y la cuarta semicorchea después de cada negra:
*----.----.----.----*----.----.----.----*----.----.----.----*----.----.----.---- Compás 4/4 estándar
*------.--.------.--*------.--.------.--*------.--.------.--*------.--.------.-- Compás de 4/4 con "shuffle"
Los asteriscos determinan las negras (4 negras por cada compás de 4/4) y los puntos determinan las semicorcheas (4 semicorcheas por cada negra). El concepto es muy sencillo, aunque a la hora de implementarlo en MIDI hay que tener en cuenta algunos aspectos importantes.
Protocolo MIDI
El protocolo MIDI es un protocolo muy sencillo por el que se envían eventos e información musical. No es objetivo de este post el explicar el protocolo ni los mensajes MIDI (cualquier búsqueda sobre "midi protocol" en la red nos dará acceso a centenares de páginas donde lo explican muy bien) aunque sí nos centraremos en los mensajes que más nos interesan de cara a implementar nuestro shuffler.
Dentro de los mensajes MIDI hay unos especiales denominados de tiempo real que son transmitidos por los secuenciadores cuando están reproduciendo una secuencia MIDI pregrabada:
0xF8: "timing clock" se envía 24 veces por cada negra.
0xFA: "start" indica que se va a iniciar la reproducción de una secuencia. Este mensaje es seguido de forma inmediata por el primer 0xF8.
0xFB: "continue" indica que se reanuda la secuencia por donde se paró.
0xFC: "stop" indica que se para la secuencia.
Por tanto, si en nuestro secuenciador musical tenemos una canción con un tempo de 120 negras por minuto, al emitir dicha secuencia por un cable MIDI, de forma intercalada con los mensaje de activación y desactivación de las notas y demás, irán entremezclados mensajes 0xF8 a razón de 24 por cada negra, es decir:
$${{120 \times 24} \over 60} = 48\;mensajes/segundo$$
Nótese que la cantidad de mensajes 0xF8 enviados por unidad de tiempo no depende de la velocidad de transmisión MIDI, sino del tempo de la secuencia musical que se esté reproduciendo. Si cada vez que nos llegue un mensaje 0xF8 desde el secuenciador vamos contando de 0 a 23 dando la vuelta de nuevo a 0 cada vez que llegamos a 24 tenemos que los mensaje 0xF8 coinciden en el tiempo con las negras y semicorcheas de la forma que indica la siguiente tabla:
n s s s
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
En esta tabla se puede ver que la negra (el beat) coincide con el contador de mensajes 0xF8 recibidos a 0 mientras que las tres semicorcheas siguientes coinciden con ese mismo contador a 6, a 12 y a 18. Ahora tenemos una base de tiempo sólida que podemos aprovechar para implementar nuestro efecto shuffle: Lo que hay que hacer es atrasar en el tiempo los mensajes de "note on" y "note off" que lleguen entre el instante 6 y el 12 y entre el instante 18 y 0 de la siguiente negra.
n s s s
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
+--------> atrasar +--------> atrasar
Dicho atraso no puede ser tal que nuestro shuffler emita notas fuera de orden por lo que el retraso en el tiempo debe ser proporcional (una nota que llegue entre los instantes 6 y el 7 será atrasada más que una que llegue entre los instantes 9 y 10 pero la primera nunca debe emitirse depués de la segunda, debemos garantizar el orden de llegada de los eventos "note on" y "note off").
Algoritmo propuesto
El MIDI shuffler se plantea como un filtro MIDI, un dispositivo con una entrada MIDI y una salida MIDI que se intercala entre el secuenciador y los sintetizadores. La salida MIDI del secuenciador irá conectada a la entrada MIDI del shuffler y la salida MIDI del shuffler irá conectada a la entrada MIDI de los secuenciadores. A continuación se plantea una propuesta de pseudocódigo para el MIDI shuffler:
iniciarShuffler
estado := ESPERAR_START_MIDI
fin iniciarShuffler
getInstanteAtrasado(t)
ret := (tamSemicorchea - tamReducido) + ((t + tamReducido) / tamSemicorchea)
devolver ret
fin getInstanteAtrasado
byteMIDIRecibido(byte)
enviar := SÍ
si (estado = ESPERAR_START_MIDI) entonces
si (byte = 0xFA) entonces
colaRetraso.borrar()
estado := ESPERAR_PRIMER_CLOCK_MIDI
fin sin
en otro caso, si (estado = ESPERAR_PRIMER_CLOCK_MIDI) entonces
si (byte = 0xF8) entonces
estado := ESPERAR_CLOCK_MIDI
contadorReloj := 6
indiceSemicorchea := 0
timer.iniciar()
fin si
en otro caso, si (estado = ESPERAR_CLOCK_MIDI) entonces
si (byte = 0xF8) entonces
contadorReloj := contadorReloj - 1
si (contadorReloj = 0) entonces
si ((indiceSemicorchea = 0) ó (indiceSemicorchea = 2)) entonces
tamSemicorchea = timer.getValor()
tamReducido = (temSemicorchea * (100 - PERCENT)) / 100
fin si
contadorReloj := 6
indiceSemicorchea := (indiceSemicorchea + 1) mod 4
timer.parar()
timer.iniciar()
fin si
en otro caso, si (esEventoNota(byte) y ((indiceSemicorchea = 1) ó (indiceSemicorchea = 3)) entonces
t := getInstanteAtrasado(timer.getValor())
colaRetraso.meter({byte, t})
enviar := NO
en otro caso, si (byte = 0xFC)
estado := ESPERAR_START_MIDI
fin si
fin si
si (enviar = SÍ) entonces
enviar(byte)
fin si
fin byteMIDIRecibido
principal
siempre hacer
si ((indiceSemicorchea = 1) ó (indiceSemicorchea = 3)) entonces
t := timer.getValor()
mientras (colaRetraso.hayAlgo()) hacer
d := colaRetraso.getCabeza()
si (d.t <= t) entonces
colaRetraso.sacar()
enviar(d.byte)
en otro caso
salir del bucle
fin si
fin mientras
fin si
fin siempre
fin principal
Lo que hace el algoritmo es aprovechar el intervalo entre el midi clock 0 y el 5 para calcular el tiempo en unidades de timer que dura una semicorchea. El objeto "timer" es un timer de bastante resolución que se arranca en el instante 0 y se para en el instante 6. En ese instante 6, una vez parado el timer, se anota la cuenta del mismo como tamSemicorchea (para indicar que es el tamaño en ticks de nuestro contador de lo que dura una semicorchea) y se calcula tamReducido a partir del porcentaje de "shuffle" que queramos (un shuffle del 0% da un tamReducido = tamSemicorchea, mientras que un shuffle del 100% da un tamReducido = 0).
instante semicorchea acción
0 0 Iniciar timer de alta resolución
1
2
3
4
5
6 1 Anotar cuenta del timer, pararlo
7 y volver a iniciarlo. Encolar cualquier
8 evento "note on" o "note off" que llegue
9 en este intervalo calculando su instante
10 de emisión con una regla de tres.
11
12 2 La misma que la semicorchea 0
13
14
15
16
17
18 3 La misma que la semicorchea 1
19
20
21
22
23
Entre los instantes 6 y el 11 lo que se hace es encolar los eventos de "note on" y "note off" que vayan llegando calculándoles en el momento que llegan, en qué instante del tick del timer deben ser transmitidos haciendo una regla de tres (en getInstanteAtrasado) y metiendo cada una de estas parejas de valores (byte e instante que debe ser transmitido) en la cola "colaRetraso".
Lo mismo se hace para los instantes de tiempo 12 al 17 y 18 al 23, respectivamente.
Ya tenemos los eventos atrasados metidos en una cola (para garantizar que el orden de emisión sea el mismo que el de recepción), ahora lo que hay que hacer es emitirlos en el instante que corresponda. y de esto se encarga el procedimiento principal en su bucle infinito. Este procedimiento principal ejecuta un bucle infinito que lo que hace es inspeccionar si hay algo que enviar en la cola "colaRetraso", si hay algo que debe ser enviado (su instante de envío es menor o igual al valor actual del timer) lo envía y lo quita de la cola. El procedimiente byteMIDIRecibido es invocado cada vez que llega un byte por el puerto MIDI.
El circuito
El MIDI shuffler, como se comentó antes, hace de filtro MIDI con una entrada y una salida. La cantidad de efecto shuffle se controla mediante un potenciómetro conectado a una de las entradas analógicas del Arduino.
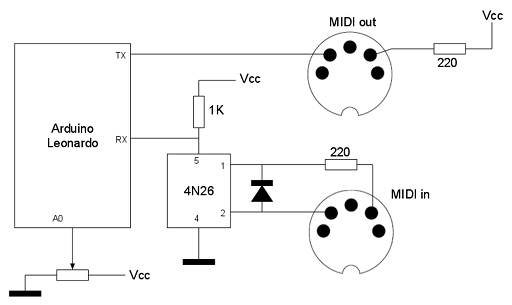
Con el potenciómetro al mínimo se aplica un efecto shuffle del 0% (sin efecto shuffle) mientras que con el potenciómetro al máximo se aplica un efecto shuffle del 50% (valores superiores al 50% genera unos resultados muy extremos).
Implementación en C++
A pesar de que en el algoritmo propuesto el procedimiento byteMIDIRecibido se supone que es invocado de forma asíncrona por el sistema cada vez que llega un byte por el puerto MIDI, lo cierto es que es más sencillo si en la rutina de interrupción de la UART encolamos los bytes MIDI que van llegando por la entrada MIDI y luego los vamos sirviendo en el bucle principal antes de comprobar el estado de la colaRetraso, haciéndolo de esta forma evitamos colisiones y la necesidad de hacer que colaRetraso sea reentrante.
int32_t MIDIShuffler::getDelayedInstant(int32_t sourceInstant) { return ((this->sixteenthNoteLength - this->reducedLength) + ((sourceInstant * this->reducedLength) / this->sixteenthNoteLength)); } void MIDIShuffler::byteReceived(uint8_t byte) { this->rxQueue.push(byte); } void MIDIShuffler::processRxByte(uint8_t byte) { bool send = true; uint8_t noChannelByte = byte & 0xF0; if (this->status == STATUS_WAIT_START_MIDI_CLOCK) { if (byte == 0xFA) { this->delayQueue.clear(); this->rxQueue.clear(); this->status = STATUS_WAIT_FIRST_MIDI_CLOCK; } } else if (this->status == STATUS_WAIT_FIRST_MIDI_CLOCK) { if (byte == 0xF8) { this->status = STATUS_WAIT_MIDI_CLOCK; this->clockCounter = CLOCK_PER_SIXTEENTH_NOTE; this->sixteenthNoteIndex = 0; this->timeCounter->start(); } } else if (this->status == STATUS_WAIT_MIDI_CLOCK) { if (byte == 0xF8) { this->clockCounter--; if (this->clockCounter == 0) { if ((this->sixteenthNoteIndex == 0) || (this->sixteenthNoteIndex == 2)) { this->sixteenthNoteLength = this->timeCounter->getValue(); this->reducedLength = (this->sixteenthNoteLength * (100 - this->percentProvider->getPercent())) / 100; } this->clockCounter = CLOCK_PER_SIXTEENTH_NOTE; this->sixteenthNoteIndex = (this->sixteenthNoteIndex + 1) & 3; // ... % 4 this->timeCounter->stop(); this->timeCounter->start(); } } else if ((noChannelByte < 0xA0) && ((this->sixteenthNoteIndex == 1) || (this->sixteenthNoteIndex == 3)) && !this->byPass) { DelayedMIDIByte d(this->getDelayedInstant(this->timeCounter->getValue()), byte); this->delayQueue.push(d); send = false; } else if (byte == 0xFC) this->status = STATUS_WAIT_START_MIDI_CLOCK; } if (send && (this->sender != NULL)) this->sender->sendByte(byte); } void MIDIShuffler::init(MIDISender &sender, PercentProvider &percentProvider, TimeCounter &timeCounter) { MIDIFilter::init(sender); this->percentProvider = &percentProvider; this->delayQueue.clear(); this->rxQueue.clear(); this->status = STATUS_WAIT_START_MIDI_CLOCK; this->timeCounter = &timeCounter; this->byPass = false; this->sixteenthNoteIndex = 0; } void MIDIShuffler::run() { if (this->rxQueue.hasElements()) { uint8_t byte = this->rxQueue.getHead(); this->processRxByte(byte); this->rxQueue.pop(); } if (((this->sixteenthNoteIndex == 1) || (this->sixteenthNoteIndex == 3)) && this->delayQueue.hasElements()) { int32_t t = this->timeCounter->getValue(); while (this->delayQueue.hasElements()) { DelayedMIDIByte d = this->delayQueue.getHead(); if (d.t <= t) { this->delayQueue.pop(); if (this->sender != NULL) this->sender->sendByte(d.byte); } else break; } } }
A continuación puede verse un vídeo con el MIDI shuffler en acción (obviamente, hay que poner el audio para que se oiga :-) )
Todo el código fuente puede descargarse de la sección soft.
[ añadir comentario ] ( 3263 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 15948 )
( 3 / 15948 )Transmitir una señal modulada en FM dentro de la banda de frecuencias de la FM comercial utilizando FPGAs es un tópico ampliamente cubierto en decenas de webs y vídeos online pero que en pocos casos es desgranado y explicado de forma entendible y rigurosa. A lo largo de este post se desarrollará tanto la base teórica como una prueba de concepto de un transmisor FM basado en FPGA.
Los fundamentos
La modulación FM consiste en hacer variar la frecuencia de la señal que estamos mandando a la antena en función de la amplitud de la señal moduladora (sonido, por ejemplo). El rango de frecuencias reservado para emisoras comerciales de audio abarca desde los 87.5 MHz hasta los 108 MHz (es el rango que recoge cualquier receptor FM analógico) con una profundidad de modulación de +- 75 KHz. Esto significa que si queremos emitir en la frecuencia de 100 MHz debemos hacer variar la frecuencia entre 99.925 MHz y 100.075 MHz en función de la amplitud de la señal moduladora.
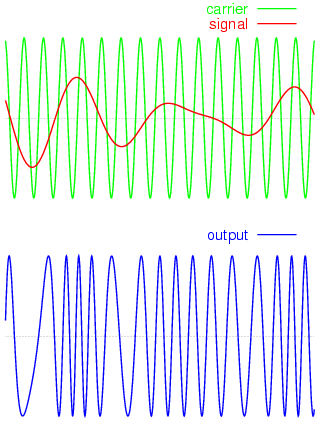
(imagen extraida de Wikipedia, con licencia Creative Commons Attribution - Share Alike 2.0, autor Gvf)
Generar la señal en el dominio digital
Intentar hacer un transmisor FM utilizando una FPGA nos hace chocar, a priori, con un primer impedimento: Poder generar una señal que varíe de frecuencia de una forma tan ligera. Hay que tener en cuenta que con una anchura de modulación de 150 KHz (75 KHz + 75 KHz) y asumiendo una señal sonora muestreada a 16 bits tenemos que la variación de la señal de salida de la antena debe de ser en pasos de:
$${150000 \over {2^{16}}} = {150000 \over 65536} = 2.2888 Hz$$
Esos son muy pocos hercios. En el dominio digital lo habitual para modificar la frecuencia de una señal es multiplicarla por una constante (mediante un PLL) o dividirla entre una constante (mediante un divisor de frecuencias). Los PLLs son circuitos híbridos (entre analógicos y digitales), no son todo lo rápido que nos gustaría (lo normal es que un PLL necesite varios ciclos hasta estabilizarse en la frecuencia deseada), normalmente trabajan con factores constantes (no variables como en nuestro caso) y no están siempre disponibles en las FPGAs para uso directo del usuario. Los divisores de frecuencia son más fáciles de hacer (no dejan de ser baterías de biestables) pero, como su propio nombre indica, sólo son capaces de dividir la frecuencia entre un valor entero.
Acumuladores de fase
Existe, sin embargo, una forma bastante ingeniosa para la síntesis directa de señales digitales sin necesidad del uso de PLLs ni de divisores de frecuencia: los acumuladores de fase. Un acumulador de fase es una de las partes que integran un oscilador digital basado en tabla de ondas. Imaginemos que queremos generar una onda senoidal mediante una tabla de ondas.
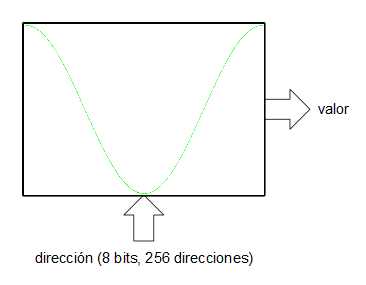
Asumiremos, por simplificar, que la tabla de la onda (realmente sería una ROM o una RAM) tiene un tamaño de 256 muestras ($2^8$). Por otro lado tenemos un registro (al que llamaremos acumulador de fase) de 16 bits y lo que hacemos es indexar la tabla de ondas utilizando los 8 bits más significativos del acumulador de fase. Las entradas D de los biestables de este registro se conectan a la salida un sumador que suma las salidas Q (el valor actual de registro) más un valor de entrada de 16 bits. En cada flanco de subida del reloj del sistema el registro (el acumulador de fase) se carga con el valor de las entradas D procedentes del sumador. En cada tick de reloj el acumulador va acumulando el valor de la entrada de 16 bits.
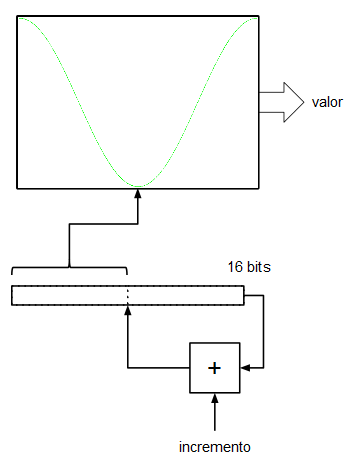
Si en la entrada de 16 bits ponemos un 0, el registro se quedará "quieto", no cambiará su valor y, por tanto la salida de datos de la ROM indexada por dicho registro sacará un valor constante (frecuencia de 0 Hz). Si en la entrada de 16 bits ponemos un 1, en registro se irá incrementando de 1 en 1, sin embargo, como lo que indexa a la tabla de valores son los 8 bits más significativos, este índice sólo avanzará cada 256 pulsos de reloj del sistema. Esto significa que con una frecuencia de reloj de 32 KHz, nuestro oscilador generaría una señal con una frecuencia de:
$${32000 \over 256} = 125 Hz$$
Yéndonos al otro extremo, si en la entrada de 16 bits metemos un valor de $2^{15} = 32768$, el acumulador de fase, al ser de 16 bits, se desbordará cada dos ciclos de reloj: el acumulador de fase generará la secuencia de valores 0, 32768, 0, 32768, 0, 32768, etc. que, a su vez, indexarán los valores mínimo y máximo de la onda senoidal que tenemos en la tabla. Esto significa que la salida del oscilador ha alcanzado su frecuencia máxima (su frecuencia de Nyquist, de 16 KHz).
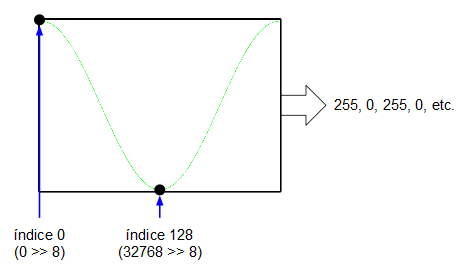
Como se puede comprobar, los incrementos en los pasos son lineales por lo que podemos establecer una especie de regla de tres para el cálculo de la frecuencia de salida de nuestro oscilador imaginario:
$$I_{acumulador fase} = {f_{deseada} \over 32000} \times 2^{16}$$
Vemos que si frecuencia_deseada = 0, entonces incremento_acumulador_fase = 0. Si frecuencia_deseada = 16000 (la frecuencia Nyquist, para 32 KHz), entonces:
$$I_{acumulador fase} = {16000 \over 32000} \times 2^{16} = {1 \over 2} \times 2^{16} = 2^{15} = 32768$$
Para 440 Hz (la nota LA de la cuarta octava del piano) tenemos que:
$$I_{acumulador fase} = {440 \over 32000} \times 2^{16} = 901.12$$
En estos casos, cuando el resultado es fraccionario, hay dos opciones: O quedarse con la parte entera (redondeando o truncando, incremento_acumulador_fase = 901), o, si no queremos perder precisión, incrementar el número de bits para reducir el error. Por ejemplo, utilizando un acumulador de fase de 59 bits conseguiríamos un valor de incremento entero (sin parte fraccionaria):
$$I_{acumulador fase} = {440 \over 32000} \times 2^{59} = 7926335344172073$$
De forma general se puede plantear la ecuación de la siguiente manera:
$$I_{acumulador fase} = {f_{deseada} \over f_{muestreo}} \times 2^{bits}$$
Nótese que la cantidad de bits que indexa la tabla de ondas no es relevante. Lo único importante es que la tabla de ondas está indexada por la parte alta del registro acumulador de fase. Como se puede apreciar, con este método es posible generar frecuencias arbitrarias con pasos relativamente pequeños y sólo limitados por el número de bits que utilicemos en el acumulador de fase.
El transmisor
Imaginemos que la frecuencia de muestreo es ahora de 320 MHz y que queremos generar una frecuencia de 100 MHz. Utilizando un acumulador de fase de 32 bits (la cantidad de bits elegida es arbitraria) tendríamos que:
$$I_{acumulador fase} = {100000000 \over 320000000} \times 2^{32} = 1342177280$$
Como se comentó antes, la cantidad de bits de resolución a la hora de indexar la tabla de ondas no es relevante a efectos de frecuencia (aunque sí a efectos de distorsión armónica y de relación señal/ruido). En nuestro caso, como no disponemos de un DAC sino que vamos a generar una señal cuadrada directamente, en teoría lo que necesitamos es una tabla con una onda cuadrada de tal forma que cuando esté en el máximo emita un 1 y cuando esté en el mínimo emita un 0.
Si asumimos que en la tabla de ondas vamos a meter una onda cuadrada con un ciclo de trabajo del 50% (perfectamente cuadrada), esto significará que la mitad de la tabla de ondas va a estar al valor mínimo (0 por ejemplo) y la otra mitad al valor máximo (255 por ejemplo, si es una ROM de 8 bits sin signo). Si al final vamos a traducir la salida de la tabla de ondas como un 0 si está en el valor mínimo y como un 1 si está en el valor máximo, es obvio que la salida de la tabla de ondas coincidirá con el valor del bit más significativo del acumulador de fase.
Y he aquí la "magia" del invento: Usando un único registro con un sumador podemos hacer un oscilador de onda cuadrada para el que podemos controlar la frecuencia de forma precisa entre 0 Hz y la mitad de la frecuencia de reloj. La precisión a la hora de ajustar la frecuencia nos la dará la cantidad de bits que usemos.
El jittering
Cualquier incremento en el acumulador de fase que no sea potencia de dos va a generar un efecto jitter en la señal de salida haciendo que ésta muchas veces diste de ser una señal cuadrada perfecta. Esto, como es obvio, provocará que la cantidad de armónicos que se generen se dispare. Vamos a verlo con un ejemplo.
Imaginemos el caso anterior: 320 MHz de frecuencia de reloj, un acumulador de fase de 32 bits y un incremento para el acumulador de fase igual a 1342177280. Aplicando este acumulador de fase obtenemos la siguiente salida (correspondiente al bit más significativo):
1 1 0 1 1 0 1 1 0 0 1 0 0 1 0 0 ... la secuencia se repite indefinidamente
Como se puede observar esta secuencia de bits dista mucho de parecerse a una señal cuadrada con ciclo de trabajo del 50%, en concreto genera tres pulsos anchos más juntos y luego dos pulsos estrechos más separados. Sin embargo si hacemos el análisis de Fourier de esta secuencia, tratándola como si fuese una señal, calculándole la transformada de Fourier usando un software numérico como Octave:
octave> abs(fft([1 1 0 1 1 0 1 1 0 0 1 0 0 1 0 0])) ans = 8.00000 1.79995 0.00000 1.01959 0.00000 5.12583 0.00000 1.20269 0.00000 1.20269 0.00000 5.12583 0.00000 1.01959 0.00000 1.79995
Vemos que la transformada de Fourier resultante es efectivamente simétrica (quitando la posición 0, que es la componente de continua), al tratarse de una señal real, y que, descartando la componente de continua (el índice 0 del vector), hay un máximo en el índice 5 del vector. Por las propiedades de la transformada de Fourier en este caso la posición 8 (el centro del vector y el centro de simetría) se corresponde con la frecuencia Nyquist que, al ser la frecuencia de reloj de 320 MHz, sería de 160 MHz (la mitad de la frecuencia del reloj). El máximo situado en la posición 5 del vector se corresponderá, siguiendo una regla de tres, con la frecuencia de:
$${{160000000 \times 5} \over 8} = 100000000 = 100 MHz$$
En efecto, la frecuencia fundamental (el máximo en la transformada de Fourier) de la señal de salida es de 100 MHz, que era nuestro objetivo, aunque como se puede ver en el análisis de Fourier, también se emitirán armónicos de 20 MHz (el valor 1.79995 se corresponde con la frecuencia ${{160 \times 1} \over 8}$), de 60 MHz (${{160 \times 3} \over 8}$) y de 140 MHz (${{160 \times 7} \over 8}$), aunque de menor amplitud.
Implementación y prueba de concepto
Como se va a emitir el sonido por radio FM y aún no disponemos de un ADC que permita la lectura de una fuente externa de audio, se generará la señal de audio dentro de la propia FPGA.
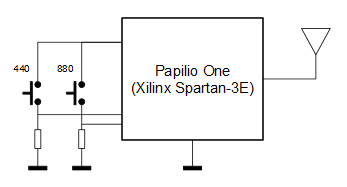
El sistema consta de dos entradas conectadas a sendos botones y que permiten seleccionar la frecuencia del tono a transmitir: cuando no se pulsa ningún botón no se modula (se genera la portadora sin modular), cuando se pulsa el botón “440” la portadora se modula con una señal cuadrada de 440 Hz (nota LA en la cuarta octava del piano), mientras que si se pulsa el botón “880” la portadora se modula con una señal cuadrada de 880 Hz (nota LA en la quinta octava del piano).
La única salida del sistema es la salida de la antena, que va a un trozo de cable que se coloca al aire. No es necesario nada más si vamos a colocar el receptor a pocos metros de la FPGA. En el caso de que queramos conectar la salida a una antena real y que queramos más potencia habría que colocar circuitos acondicionadores y/o amplificadores a la salida y, sobretodo, filtros: hay que recordar que la señal de salida es una onda cuadrada repleta de armónicos.
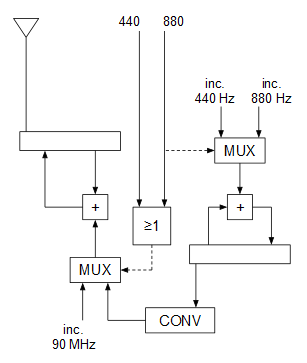
En reposo, las entradas “440” y “880” valen 0, por lo que el MUX inferior selecciona la entrada del incremento correspondiente a los 90 MHz (portadora sin modular). Cuando se pulsa sólo el botón “440” el MUX inferior deja pasar la señal moduladora (ya convertida en secuencias de incrementos en lugar de en 0 y 1) a la entrada del oscilador para modularlo, y cuando se pulsa el botón “880” ocurre lo mismo con el MUX inferior y, además, al cambiar la entrada de selección del MUX superior, cambia el incremento del oscilador que genera la señal moduladora para que genere 880 Hz en lugar de 440 Hz.
El módulo combinacional CONV convierte la entrada de 1 bit (0 o 1) proveniente del oscilador de 440 u 880 Hz, en una salida de 32 bits que es el incremento de fase de correspondiente a cada nivel de la señal moduladora:
0 --> 1341058799
1 --> 1343295761
En este caso se ha realizado una implementación sobre una FPGA Spartan-3E de Xilinx con un reloj externo de 32 MHz (papilio one). Las Spartan-3E disponen de varios DCM (Digital Clock Managers) que permiten subir la frecuencia de reloj mediante multiplicadores. En este caso, con un reloj a 32 MHz la máxima frecuencia que se puede alcanzar es de 288 MHz, por lo que ajustamos los cálculos a dicha frecuencia y asumiendo que vamos a transmitir en la banda de 90 MHz.
$$I_{acumulador fase} = {90000000 \over 288000000} \times 2^{32} = 1342177280$$
Como la señal moduladora (los tonos de 440 y 880 Hz) van a ser también ondas cuadradas, sólo hay que calcular los incrementos para el 0 y el 1 de la señal moduladora (en este caso no hay valores intermedios). El 0 de la señal moduladora lo asociaremos a 89,925 MHz y el 1 de la señal moduladora lo asociaremos a 90,075 MHz (recordemos que la profundidad de modulación en la FM comercial es de 75 KHz).
$$I_{89.925} = {89925000 \over 288000000} \times 2^{32} \approx 1341058799$$
$$I_{90.075} = {90075000 \over 288000000} \times 2^{32} \approx 1343295761$$
A continuación puede verse el código fuente:
library ieee; use ieee.std_logic_1164.all; use ieee.numeric_std.all; entity FMTransmitter is port ( Clk : in std_logic; Reset : in std_logic; Button440 : in std_logic; Button880 : in std_logic; AntOut : out std_logic ); end entity; architecture Architecture1 of FMTransmitter is component Oscillator is generic ( NBits : integer := 32 ); port ( IncrementIn : in std_logic_vector(31 downto 0); Clk : in std_logic; Reset : in std_logic; DataOut : out std_logic ); end component; component Mux2Inputs is generic ( NBits : integer := 32 ); port ( Sel : in std_logic; DataIn0 : in std_logic_vector((NBits - 1) downto 0); DataIn1 : in std_logic_vector((NBits - 1) downto 0); DataOut : out std_logic_vector((NBits - 1) downto 0) ); end component; signal Mux1Out : std_logic_vector(31 downto 0); signal Mux1Sel : std_logic; signal ConvOut : std_logic_vector(31 downto 0); signal ConvIn : std_logic; signal Mux2Out : std_logic_vector(31 downto 0); begin RadioOsc : Oscillator generic map ( NBits => 32 ) port map ( Clk => Clk, Reset => Reset, IncrementIn => Mux1Out, DataOut => AntOut ); Mux1Sel <= Button440 or Button880; Mux1 : Mux2Inputs generic map ( NBits => 32 ) port map ( Sel => Mux1Sel, DataIn0 => std_logic_vector(to_unsigned(1342177280, 32)), -- center freq = 90.0 MHz DataIn1 => ConvOut, DataOut => Mux1Out ); -- center freq - 75 KHz when 0 -- center freq + 75 KHz when 1 ConvOut <= std_logic_vector(to_unsigned(1341058799, 32)) when (ConvIn = '0') else std_logic_vector(to_unsigned(1343295761, 32)); AudioOsc : Oscillator generic map ( NBits => 32 ) port map ( Clk => Clk, Reset => Reset, IncrementIn => Mux2Out, DataOut => ConvIn ); Mux2 : Mux2Inputs generic map ( NBits => 32 ) port map ( Sel => Button880, DataIn0 => std_logic_vector(to_unsigned(6562, 32)), -- 440 Hz DataIn1 => std_logic_vector(to_unsigned(13124, 32)), -- 880 Hz DataOut => Mux2Out ); end architecture;
Tanto el oscilador de salida (el de alta frecuencia) como el oscilador de audio se han implementado usando el mismo componente “Oscillator.vhd”.
library ieee; use ieee.std_logic_1164.all; use ieee.numeric_std.all; use ieee.std_logic_signed.all; entity Oscillator is generic ( NBits : integer := 32 ); port ( IncrementIn : in std_logic_vector(31 downto 0); Clk : in std_logic; Reset : in std_logic; DataOut : out std_logic ); end entity; architecture Architecture1 of Oscillator is component Reg is generic ( NBits : integer := 32 ); port ( Enable : in std_logic; Clk : in std_logic; DataIn : in std_logic_vector((NBits - 1) downto 0); DataOut : out std_logic_vector((NBits - 1) downto 0) ); end component; signal MuxOut : std_logic_vector((NBits - 1) downto 0); signal RegOut : std_logic_vector((NBits - 1) downto 0); begin PhaseAcc : Reg generic map ( NBits => NBits ) port map ( Enable => '1', Clk => Clk, DataIn => MuxOut, DataOut => RegOut ); MuxOut <= (others => '0') when (Reset = '1') else (RegOut + IncrementIn); DataOut <= RegOut(NBits - 1); end architecture;
El tipo de sumador
En otros proyectos FPGA anteriormente abordados en este blog, cada vez que hacía falta un sumador se tiraba de un sumador estándar implementado mediante lógica combinatoria (“Adder.vhd”). Hasta ahora se ha hecho así por razones pedagógicas. En este caso, sin embargo, al estar el reloj a una frecuencia extremadamente alta para la FGPA ha sido necesario el uso del operador “+”. Este operador garantiza “la mejor implementación” de la suma para la plataforma y esto se traduce, en el caso del Spartan-3E y en el caso de la mayoría de las FPGAs existentes, en que se va a hacer uso de sumadores que ya se encuentran integrados (“hardwired”) en el sustrato de todas las FPGA (todos los fabricantes los incluyen, de mayor o menor cantidad de bits).
¿Qué ventajas tienen estos sumadores con respecto al sumador que hemos estado usando hasta ahora? La principal diferencia es que en nuestro “Adder.vhd” el acarreo es en cascada, mientras que los sumadores implementados a fuego en las FPGAs están basados siempre en circuitos CLA (Carry Look Ahead), que permiten precalcular los acarreos de cada bit sin necesidad de que estén calculados los bits anteriores. Aún siendo circuitos combinacionales tanto los unos como los otros, el tiempo de propagación del resultado en el caso de sumadores con CLA es mucho menor que en el caso de sumadores con acarreo en cascada (como el “Adder.vhd” que hemos usado hasta ahora en los proyectos).
En nuestro caso concreto se da además la circunstancia que, con un reloj a 288 MHz, el sumador con acarreo en cascada (el “Adder.vhd” de siempre) da problemas de timing o, lo que es lo mismo, “no le da tiempo de sumar tan rápido” y no queda otra opción que tirar del operador “+” (cosa que, por otro lado, es lo recomendable ya que se garantiza siempre la mejor implementación).
Vídeo
A continuación un pequeño fragmento de vídeo donde se puede ver y escuchar el invento en funcionamiento. La calidad del audio es bastante baja: usé mi radio-despertador como receptor, en el receptor del móvil se oye mucho mejor… pero no hubiese podido grabarlo :-)
Espero que haya resultado interesante. Todo el código fuente se puede descargar de la sección soft.
[ añadir comentario ] ( 3508 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 6075 )
( 3 / 6075 )
 Calendario
Calendario




