Mecánica del juego
Se trata de shooter 3D simplificado: hay que buscar todos los items blancos y dispararles con A para que desaparezcan. En el momento que hemos terminado con todos los items de un nivel, nos vamos al siguiente nivel, y así sucesivamente. En el juego no puedes "morir" simplemente vas cambiado de niveles y cuando terminas el último vuelves a empezar.
Diseño de la pantalla
La única pantalla que tiene el juego está gestionada por la clase TanksMainScreen (en la carpeta games/tanksfp). El dibujado de la escena 3D se realiza en el centro de la pantalla (64x64 pixels). Las zonas de los lados se utilizan para indicar cuantos items o enemigos quedan por abatir en el nivel actual y el número del nivel.
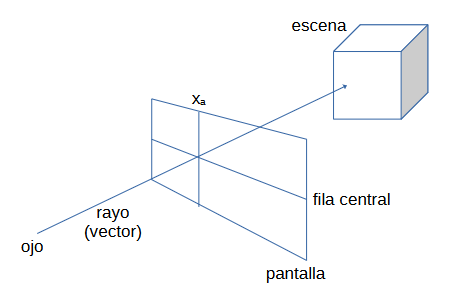
Renderizado de la escena usando raycasting
La técnica del raycasting, la utilizada en muchos de los juegos 3D de los años 90 y principios de los 2000 para dibujar escenas en 3D, se basaba realmente en el cálculo de colisiones de vectores bidimensionales. Para cada columna de la pantalla se calcula un vector 2D (rayo) que va desde el jugador hasta la escena pasando por ese punto de la pantalla.
Si el vector choca con algún muro u objeto, se calcula la distancia a la que choca dicho vector y, por semejanza de triángulos con respecto a la altura del muro u objeto contra el que ha chocado el rayo, se calcula la altura que debe tener esa sección del objeto en la coordenada x por la que ha pasado el rayo.
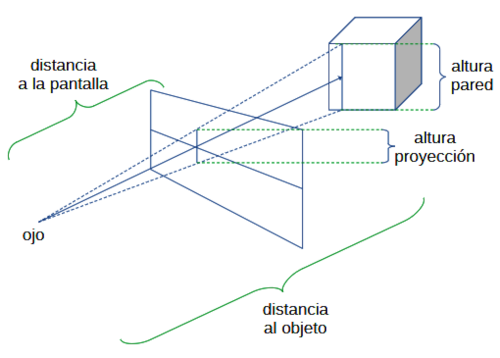
En este caso:
$$\frac{altura\ proyección}{distancia\ a\ la\ pantalla} = \frac{altura\ objeto}{distancia\ al\ objeto}$$
Se define un mundo en dos dimensiones en el que los muros y los items son segmentos y el jugador se mueve en el plano 2D:
const Level TanksMainScreen::LEVELS[] = { { // nivel 0 /* +---+ cada | | es un cuadrado de 10x10 unidades del mundo, P es el jugador +---+ +---+---+---+---+---+---+---+---+ | | + P--> + + | | | + +---+---+---+ | | +---+---+---+---+ + | | | + + + | | | + + + | | +---+---+---+---+---+---+---+---+ */ 80, // width = 80 (integer) 60, // height = 60 (integer) 8, // 8 segments { {{0, 0}, {5242880, 0}}, // scene segments (Q16.16 fixed point) {{5242880, 0}, {5242880, 3932160}}, {{5242880, 3932160}, {0, 3932160}}, {{0, 3932160}, {0, 0}}, {{0, 1966080}, {2621440, 1966080}}, {{2621440, 1966080}, {2621440, 3276800}}, {{3276800, 655360}, {3276800, 1310720}}, {{3276800, 1310720}, {5242880, 1310720}} }, {655360, 655360}, // (10, 10) (Q16.16 fixed point) 0, // player at (10, 10) looking with ANGLE[0] 2 // 2 collectable/shootable items }, // ... other levels };
El algoritmo de pintado "lanza" los 64 rayos correspondientes las 64 columnas de la ventana de la escena 3D (el recuadro de 64x64 pixels que se dibuja en el centro del display LCD) y para cada rayo, se calcula la intersección del mismo con cada uno de los segmentos del mundo y los enemigos (del nivel).
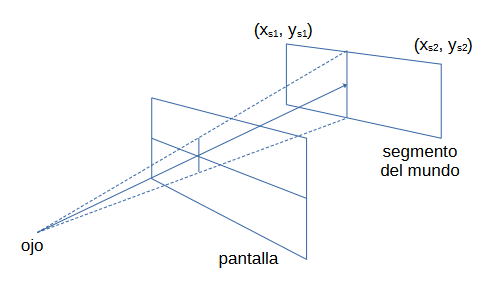
Cada segmento del mundo tendrá dos coordenadas 2D asociadas, mientras que cada rayo estará compuesto por la coordenada del jugador más un vector director unitario apuntando a la columna del display correspondiente. En cada frame, las coordenadas del jugador no cambian, lo que cambia es el vector director (el rayo).
El algoritmo grosso modo sería el siguiente:
para cada coordenada x entre -31 y +31 (se asume que 0 es el centro de la pantalla)
rayo = vector unitario que va desde el jugador y apunta a la columna x
distanciaColision = infinita
segmentoAPintar = ninguno
para cada segmento s del nivel
calcular las posible colisión entre el rayo y s
si colisiona y (distancia < distanciaColision) entonces
distanciaColision = distancia
segmentoAPintar = s
fin si
fin para
si (segmentoAPintar != ninguno) entonces
alturaEnPantalla = ALTURA * distanciaAPantalla / distanciaColision
pintar en la columna x un segmento vertical de tamaño alturaEnPantalla
en caso contrario
pintar en la columna x un punto en el centro (horizonte)
fin si
fin para
Cálculo de las colisiones
Cada segmento $s$ del mundo tendrá dos coordenadas 2D asociadas:
$$
\left( \left( x_{s1}, y_{s1} \right), \left( x_{s2}, y_{s2} \right) \right)
$$
Mientras que cada uno de los 64 rayos que se "lanzan" será un vector de la forma
$\left( \left( x_r , y_r \right), \left( x_{rd} , y_{rd} \right) \right)$ siendo $\left( x_r , y_r \right)$ las coordenadas del jugador en el mapa y $\left( x_{rd} , y_{rd} \right)$ el vector director unitario que apunta hacia el pixel.
Si definimos los puntos del segmento usando ecuaciones paramétricas, tenemos que:
$$
x = x_{s1} + t \left( x_{s2} - x_{s1} \right)\\
y = y_{s1} + t \left( y_{s2} - y_{s1} \right)
$$
Siendo $0 \leq t \leq 1$, de tal manera que:
$$
t = 0 \Rightarrow \left( x, y \right) = \left( x_{s1}, y_{s1} \right)\\
t = 1 \Rightarrow \left( x, y \right) = \left( x_{s2}, y_{s2} \right)
$$
Mientras que si definimos los puntos a lo largo del rayo que trazamos desde el jugador hasta la columna de la pantalla tenemos que:
$$
x = x_{r} + u x_{rd}\\
y = y_{r} + u y_{rd}
$$
Siendo $0 \le u$ y $u$ la distancia desde el jugador hasta $\left( x, y \right)$. A continuación definimos $d_{xs} = x_{s2} - x_{s1}$ y $d_{ys} = y_{s2} - y_{s1}$ y despejamos:
$$
x = x_{s1} + t d_{xs} = x_{r} + u x_{rd}\\
y = y_{s1} + t d_{ys} = y_{r} + u y_{rd}\\
t = \frac{x_{r} + u x_{rd} - x_{s1}}{d_{xs}}\\
u = \frac{y_{s1} + t d_{ys} - y_{r}}{y_{rd}}
$$
Por tanto:
$$
u = \frac{y_{s1} + \frac{x_{r} + u x_{rd} - x_{s1}}{d_{xs}} d_{fs} - y_{r}}{y_{rd}}\\
u y_{rd} = y_{s1} + \frac{x_{r} d_{ys}}{d_{xs}} + u \frac{x_{rd} d_{ys}}{d_{xs}} - \frac{x_{s1} d_{ys}}{d_{xs}} - y_{r}\\
u y_{rd} - u \frac{x_{rd} d_{ys}}{d_{xs}} = y_{s1} + \frac{x_{r} d_{ys}}{d_{xs}} - \frac{x_{s1} d_{ys}}{d_{xs}} - y_{r}\\
u \left( y_{rd} - \frac{x_{rd} d_{ys}}{d_{xs}} \right) = y_{s1} + \frac{x_{r} d_{ys}}{d_{xs}} - \frac{x_{s1} d_{ys}}{d_{xs}} - y_{r}\\
u = \frac{y_{s1} + \frac{x_{r} d_{ys}}{d_{xs}} - \frac{x_{s1} d_{ys}}{d_{xs}} - y_{r}}{y_{rd} - \frac{x_{rd} d_{ys}}{d_{xs}}}
$$
Multiplicando numerador y denominador por $d_{xs}$:
$$
u = \frac{d_{xs} y_{s1} + x_{r} d_{ys} - x_{s1} d_{ys} - y_{r} d_{xs}}{y_{rd} d_{xs} - x_{rd} d_{ys}}
$$
De esta forma ya tenemos calculado $u$ que será la distancia entre el jugador y la recta que contiene el segmento $s$. si $u < 0$ significará que el segmento está detrás del jugador.
Ahora con $u$ calculado, podemos sustituir su valor en:
$$
t = \frac{x_{r} + u x_{rd} - x_{s1}}{d_{xs}}
$$
Lo que nos dará el valor de $t$. Si $t < 0$ o $t > 1$ significará que el rayo no corta con el segmento. Nótese que si $y_{rd} d_{xs} - x_{rd} d_{ys} = 0$ significará que el rayo y la recta que contiene el segmento no se cortan (son paralelos) y debe ser tenido en cuenta para evitar una división entre 0:
TanksMainScreen::Intersection TanksMainScreen::getIntersection(const Segment &seg, const Vector &ray, const fixedpoint_t minRayT, fixedpoint_t &segT, fixedpoint_t &rayT) { fixedpoint_t dxs = seg.p2.x - seg.p1.x; fixedpoint_t dys = seg.p2.y - seg.p1.y; if ((dxs != 0) || (dys != 0)) { fixedpoint_t denRayT = (ray.dir.y * dxs) - (ray.dir.x * dys); if (denRayT != 0) { rayT = ((dxs * seg.p1.y) + (ray.p.x * dys) - (seg.p1.x * dys) - (ray.p.y * dxs)) / denRayT; if (rayT >= minRayT) { if (dxs != 0) segT = (ray.p.x + (rayT * ray.dir.x) - seg.p1.x) / dxs; else segT = (ray.p.y + (rayT * ray.dir.y) - seg.p1.y) / dys; if ((segT >= 0) && (segT <= fixedpoint_t::get(1))) return Intersection::ONE_POINT; } } } return Intersection::NO_POINT; }
Optimizaciones y datos precalculados
Todos los cálculos de precisión decimal se realizan utilizando aritmética de punto fijo en formato Q16.16 (enteros de 32 bits con 16 bits para la parte entera y 16 bits para la parte fraccionaria) y ayudándonos de la sobrecarga de operadores para facilitar la escritura de código y la mantenibilidad del mismo.
class fixedpoint_t { public: int32_t v; fixedpoint_t(int32_t x = 0) : v(x) { }; inline fixedpoint_t &operator = (const int32_t &x) { this->v = x << 16; return *this; }; inline fixedpoint_t operator + (const fixedpoint_t &x) const { fixedpoint_t ret; ret.v = this->v + x.v; return ret; }; inline fixedpoint_t operator - (const fixedpoint_t &x) const { fixedpoint_t ret; ret.v = this->v - x.v; return ret; }; inline fixedpoint_t operator - () const { fixedpoint_t ret; ret.v = -(this->v); return ret; }; inline fixedpoint_t operator * (const fixedpoint_t &x) const { fixedpoint_t ret; ret.v = (((int64_t) this->v) * ((int64_t) x.v)) >> 16; return ret; }; inline fixedpoint_t operator / (const fixedpoint_t &x) const { fixedpoint_t ret; ret.v = (((int64_t) this->v) << 16) / ((int64_t) x.v); return ret; }; inline bool operator == (const fixedpoint_t &x) const { return (this->v == x.v); }; inline bool operator != (const fixedpoint_t &x) const { return (this->v != x.v); }; inline bool operator < (const fixedpoint_t &x) const { return (this->v < x.v); }; inline bool operator > (const fixedpoint_t &x) const { return (this->v > x.v); }; inline bool operator <= (const fixedpoint_t &x) const { return (this->v <= x.v); }; inline bool operator >= (const fixedpoint_t &x) const { return (this->v >= x.v); }; inline fixedpoint_t operator += (const fixedpoint_t &x) { this->v += x.v; return *this; }; inline fixedpoint_t operator -= (const fixedpoint_t &x) { this->v -= x.v; return *this; }; inline int32_t getIntegerPart() { return this->v >> 16; }; inline static fixedpoint_t get(int32_t x) { fixedpoint_t ret; ret.v = x << 16; return ret; }; };
Además existen dos puntos clave en el código donde son necesarios cálculos trigonométricos:
1. El jugador está definido por sus coordenadas y por un vector unitario que apunta a "donde está mirando". Dicho vector coincide con el vector del rayo para la columna 0 de la pantalla por lo que cada rayo será una rotación del vector "hacia donde estoy mirando" y las rotaciones se deben calcular mediante senos y cosenos, así que lo que se hace en este caso es generar unas tablas precalculadas con los senos y los cosenos de los diferentes ángulos necesarios para calcular los 64 rayos de la pantalla. De hecho no hacen falta 64 senos y cosenos, basta con 32, puesto que la pantalla es simétrica.
2. Para que el jugador gire, se hace una rotación de su vector director alrededor de la coordenada del propio jugador y dicha rotación se realiza también aprovechando tablas precalculadas de senos y cosenos sólo para un cuadrante (son simétricos cambiándoles el signo para los otros tres cuadrantes de la circunferencia goniométrica).
Para ayudarnos en la generación de datos precalculados se hacen dos scripts:
- calculate_dir_vector.sh NUM_ÁNGULOS: Genera una tabla precalculada con los senos y los cosenos de NUM_ÁNGULOS en el intervalo $\left[ 0 , \frac{\pi}{2} \right)$. Los valores generador en formato de punto fijo Q16.16 (directamente "copiables y pegables" en el código C++).
- calculate_display_angles.sh DIST_TO_CENTER DISPLAY_WIDTH: Genera una tabla precalculada de 32 registros. Cada registro contiene un ángulo en radianes (no se usa en el código), el seno de ese ángulo, el coseno de ese ángulo y la distancia desde el jugador hasta el punto de la pantalla (el valor "distanciaAPantalla" necesario para calcular correctamente la altura de los objetos proyectados). DIST_TO_CENTER es la distancia desde el jugador hasta el centro de la pantalla en unidades del mundo y DISPLAY_WIDTH es la anchura de la pantalla en unidades del mundo.
A continuación se puede ver cómo queda el código que calcula el trazado de rayos de la pantalla a partir del vector del jugador:
const AngleAndDistance TanksMainScreen::DISPLAY_ANGLES_AND_DISTANCES[32] = { // precalculated vector of angles and distances to display from player // DISPLAY_ANGLES_AND_DISTANCES(i).angle = the angle in radians from center os display of pixel located at center +/- i (not used in code) // DISPLAY_ANGLES_AND_DISTANCES(i).cosineAngle = cos(angle) // DISPLAY_ANGLES_AND_DISTANCES(i).sineAngle = sin(angle) // DISPLAY_ANGLES_AND_DISTANCES(i).distance = the distance in world units from player to the pixel in the display located at center +/- i {0, 65536, 0, 327680}, // ./calculate_display_angles.sh 5 15 distance from player to center of display = 5 world units, display width = 15 world units {3069, 65464, 3068, 328039}, {6126, 65249, 6117, 329116}, {9155, 64897, 9126, 330904}, {12146, 64413, 12077, 333390}, {15087, 63806, 14954, 336559}, {17967, 63088, 17743, 340393}, {20778, 62269, 20432, 344869}, {23512, 61363, 23011, 349962}, {26163, 60382, 25473, 355646}, {28726, 59340, 27815, 361893}, {31199, 58248, 30034, 368675}, {33579, 57119, 32129, 375962}, {35866, 55963, 34102, 383726}, {38060, 54791, 35956, 391939}, {40161, 53610, 37694, 400572}, {42172, 52428, 39321, 409600}, {44094, 51253, 40842, 418996}, {45931, 50088, 42262, 428736}, {47684, 48940, 43587, 438799}, {49358, 47810, 44822, 449161}, {50955, 46704, 45974, 459803}, {52480, 45622, 47048, 470705}, {53934, 44567, 48049, 481851}, {55322, 43539, 48982, 493223}, {56647, 42540, 49852, 504807}, {57912, 41570, 50664, 516587}, {59120, 40629, 51421, 528551}, {60274, 39717, 52129, 540687}, {61378, 38834, 52790, 552983}, {62433, 37979, 53408, 565429}, {63442, 37152, 53987, 578016} }; ... void TanksMainScreen::calculateRay(Vector &ray, fixedpoint_t &distToDisplay, int32_t x) { // x = -31..31 ray = this->player; fixedpoint_t cosine = 1; fixedpoint_t sine = 0; if (x < 0) { cosine = DISPLAY_ANGLES_AND_DISTANCES[-x].cosineAngle; sine = DISPLAY_ANGLES_AND_DISTANCES[-x].sineAngle; distToDisplay = DISPLAY_ANGLES_AND_DISTANCES[-x].distance; } else { cosine = DISPLAY_ANGLES_AND_DISTANCES[x].cosineAngle; sine = -DISPLAY_ANGLES_AND_DISTANCES[x].sineAngle; distToDisplay = DISPLAY_ANGLES_AND_DISTANCES[x].distance; } ray.rotate(cosine, sine); }
Y cómo queda el código que calcula el cambio del vector del jugador cuando éste se gira:
const Angle TanksMainScreen::ANGLES[16] = { // 16 angles (cosines and sines) for first quadrant (other quadrant values are calculated changing cos/sin signs) {65536, 0}, // ./calculate_dir_vector.sh 16 {65220, 6423}, {64276, 12785}, {62714, 19024}, {60547, 25079}, {57797, 30893}, {54491, 36409}, {50660, 41575}, {46340, 46340}, {41575, 50660}, {36409, 54491}, {30893, 57797}, {25079, 60547}, {19024, 62714}, {12785, 64276}, {6423, 65220} }; ... void TanksMainScreen::fillAngle(Angle &a, const uint8_t i) { if (i < 16) a = ANGLES[ i ]; else if ((i >= 16) && (i < 32)) { a.cosine = -ANGLES[i - 16].sine; a.sine = ANGLES[i - 16].cosine; } else if ((i >= 32) && (i < 48)) { a.cosine = -ANGLES[i - 32].cosine; a.sine = -ANGLES[i - 32].sine; } else if (i >= 48) { a.cosine = ANGLES[i - 48].sine; a.sine = -ANGLES[i - 48].cosine; } } ... void TanksMainScreen::rotatePlayer(RotateTo t) { if (t == RotateTo::LEFT) this->playerAngle = (this->playerAngle + 1) & 0x3F; // 0..63 else if (t == RotateTo::RIGHT) this->playerAngle = (this->playerAngle + 64 - 1) & 0x3F; // 0..63 Angle a; fillAngle(a, this->playerAngle); this->player.dir.x = a.cosine; this->player.dir.y = a.sine; }
Conclusión y siguiente entrega
El uso de raycasting combinado con el cálculo mediante aritmética de punto fijo permite a un microcontrolador de potencia muy limitada proyectar escenas básicas en 3D en tiempo real y poder disfrutar de una experiencia 3D aunque sea en una pequeña pantalla LCD de 128x64 pixels. En la siguiente entrega de esta serie relacionada con la consola GabrielBoy se abordará el diseño y la implementación del mítico juego Snake.
Todo el código y los diseños están en la sección soft.
[ añadir comentario ] ( 1635 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 2589 )
( 3 / 2589 )
 Calendario
Calendario




