Principios
Un sistema con multitarea apropiativa debe por tanto poseer mecanismos que permitan interrumpir la ejecución de la tarea actualmente en curso y que permitan también reanudar la ejecución de otra tarea que haya sido interrumpida previamente. Este mecanismo debería ser lo más transparente al usuario (a las tareas) posible por lo que normalmente se utilizan las interrupciones. Las interrupciones en la totalidad de los procesadores que las implementan (no conozco ningún procesador que no las tenga) permiten ejecutar código de forma no solicitada por la tarea actualmente en ejecución y a raiz de un evento externo al flujo actual de la tarea.
En el momento que se produce la interrupción (la causa puede ser externa al procesador: entradas de datos, pines de entrada que cambian de estado o interna: división entre cero, instrucción no reconocida, etc.) el procesador almacena en la pila del sistema la dirección de la siguiente instrucción que se va a ejecutar y hace que el contador de programa apunte a la primera instrucción del código de interrupción. Este código de interrupción que se ejecuta a raiz del evento suele denominarse ISR (Interrupt Service Routine).
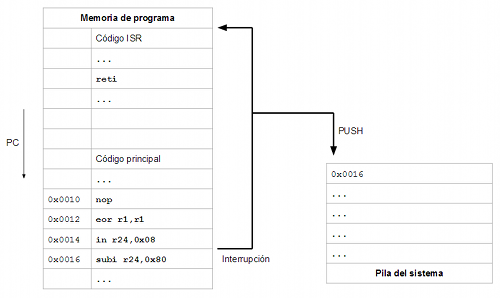
Normalmente existirán diferentes orígenes de interrupción y diferentes vectores de interrupción. Por ejemplo un procesador podría tener dos orígenes de interrupción (el cambio de estado de un pin de entrada y el desbordamiento de un contador interno) y un solo vector de interrupción por lo que se ejecutará la misma ISR para cualquiera de los dos eventos que se produzca. En estos casos, obviamente, el procesador siempre provee mecanismos para que la ISR sea capaz de discernir cuál ha sido la causa de que ella se esté ejecutando (algún registro de estado, por ejemplo).
Lo normal es tener aproximadamente la misma cantidad de orígenes de interrupción que de vectores de interrupción, de tal forma que podemos definir una ISR para cada origen de interrupción. Nótese que una ISR no es más que un trozo de código. En algunos sistemas las ISR no se diferencian en nada de una función normal (por ejemplo, ARM Cortex-M) que debe terminar como todas las funciones con algún tipo de instrucción "ret", mientras que en otros sistemas se debe utilizar algun tipo de instrucción especial normalmente a la hora de regresar: por ejemplo los microcontroladores AVR deben terminar sus funciones ISR con la instrucción "reti" (RETurn from Interrupt). Sin embargo, salvo estas excepciones, dentro de una ISR se puede poner el código que se quiera: no deja de ser un trozo de código como cualquier otro.
Una ISR sencillita
Consideremos inicialmente una ISR sencillita que vamos a compilar para Arduino Leonardo (microcontrolador ATmega32U4):
#include <avr/interrupt.h> #include <avr/io.h> #include <stdint.h> using namespace std; ISR(TIMER0_OVF_vect) { PORTC ^= 0x80; } int main() { PRR1 |= 0x80; DDRC |= 0x80; TCCR0B |= 0x05; TIMSK0 |= 0x01; sei(); while (true) ; return 0; }
$ /ruta/avr/bin/avr-g++ -std=c++11 -DF_CPU=16000000UL -mmcu=atmega32u4 -Os -g -c -o test.o test.cc
$ /ruta/avr/bin/avr-g++ -std=c++11 -DF_CPU=16000000UL -mmcu=atmega32u4 -Os -c -o test.elf test.o
Como se puede ver, usando el compilador avr-g++ se puede hacer de forma muy sencilla un código con soporte para interrupciones en C++. En este caso tenemos un sencillo blinker de toda la vida: cada vez que el Timer 0 se desborda se cambia el estado del bit de salida y hace cambiar de estado a su vez un led conectado a él. Para comprobar de forma detallada cómo funciona el invento podemos desensamblar el fichero ELF generado por el compilador:
$ /ruta/avr/bin/avr-objdump -D test.elf
En la dirección 0 de la memoria tenemos los diferentes vectores de interrupción. Como se puede apreciar está definido el vector 0 (denominado vector de reset ya que en muchos procesadores, como el AVR, el reset se trata como una interrupción más por lo que el vector de reset indica qué código debe ejecutarse nada más encenderse el procesador) y el vector 23 (que se corresponde en el ATmega32U4 con la interrupción de desbordamiento del Timer 0):
Disassembly of section .text:
00000000 <__vectors>:
0: 0c 94 56 00 jmp 0xac ; 0xac <__ctors_end>
4: 0c 94 60 00 jmp 0xc0 ; 0xc0 <__bad_interrupt>
8: 0c 94 60 00 jmp 0xc0 ; 0xc0 <__bad_interrupt>
c: 0c 94 60 00 jmp 0xc0 ; 0xc0 <__bad_interrupt>
10: 0c 94 60 00 jmp 0xc0 ; 0xc0 <__bad_interrupt>
14: 0c 94 60 00 jmp 0xc0 ; 0xc0 <__bad_interrupt>
18: 0c 94 60 00 jmp 0xc0 ; 0xc0 <__bad_interrupt>
1c: 0c 94 60 00 jmp 0xc0 ; 0xc0 <__bad_interrupt>
20: 0c 94 60 00 jmp 0xc0 ; 0xc0 <__bad_interrupt>
24: 0c 94 60 00 jmp 0xc0 ; 0xc0 <__bad_interrupt>
28: 0c 94 60 00 jmp 0xc0 ; 0xc0 <__bad_interrupt>
2c: 0c 94 60 00 jmp 0xc0 ; 0xc0 <__bad_interrupt>
30: 0c 94 60 00 jmp 0xc0 ; 0xc0 <__bad_interrupt>
34: 0c 94 60 00 jmp 0xc0 ; 0xc0 <__bad_interrupt>
38: 0c 94 60 00 jmp 0xc0 ; 0xc0 <__bad_interrupt>
3c: 0c 94 60 00 jmp 0xc0 ; 0xc0 <__bad_interrupt>
40: 0c 94 60 00 jmp 0xc0 ; 0xc0 <__bad_interrupt>
44: 0c 94 60 00 jmp 0xc0 ; 0xc0 <__bad_interrupt>
48: 0c 94 60 00 jmp 0xc0 ; 0xc0 <__bad_interrupt>
4c: 0c 94 60 00 jmp 0xc0 ; 0xc0 <__bad_interrupt>
50: 0c 94 60 00 jmp 0xc0 ; 0xc0 <__bad_interrupt>
54: 0c 94 60 00 jmp 0xc0 ; 0xc0 <__bad_interrupt>
58: 0c 94 60 00 jmp 0xc0 ; 0xc0 <__bad_interrupt>
5c: 0c 94 62 00 jmp 0xc4 ; 0xc4 <__vector_23>
60: 0c 94 60 00 jmp 0xc0 ; 0xc0 <__bad_interrupt>
64: 0c 94 60 00 jmp 0xc0 ; 0xc0 <__bad_interrupt>
68: 0c 94 60 00 jmp 0xc0 ; 0xc0 <__bad_interrupt>
6c: 0c 94 60 00 jmp 0xc0 ; 0xc0 <__bad_interrupt>
70: 0c 94 60 00 jmp 0xc0 ; 0xc0 <__bad_interrupt>
74: 0c 94 60 00 jmp 0xc0 ; 0xc0 <__bad_interrupt>
Si nos vamos al código que ha generado el compilador para la ISR correspondiente al vector 23:
000000c4 <__vector_23>:
c4: 1f 92 push r1
c6: 0f 92 push r0
c8: 0f b6 in r0, 0x3f ; 63
ca: 0f 92 push r0
cc: 11 24 eor r1, r1
ce: 8f 93 push r24
d0: 88 b1 in r24, 0x08 ; 8
d2: 80 58 subi r24, 0x80 ; 128
d4: 88 b9 out 0x08, r24 ; 8
d6: 8f 91 pop r24
d8: 0f 90 pop r0
da: 0f be out 0x3f, r0 ; 63
dc: 0f 90 pop r0
de: 1f 90 pop r1
e0: 18 95 reti
Vemos que lo primero que hace la ISR es guardar en la pila (PUSH) los registros R1, R0, SREG y R24 que son registros que utiliza ("ensucia") para hacer la operación:
PORTC ^= 0x80;
Y, tras realizar dicha operación, restaura de nuevo dichos registros en orden inverso desde la pila (POP) antes de regresar (RETI). Esta forma de operar hace que la tarea principal (el bucle infinito que hay en la función "main") no se da cuenta de que es interrumpido de forma periódica ya que la ISR se encarga de salvaguardar y restaurar los registros que utiliza de forma transparente. La función "main" como mucho puede notar que cada cierto tiempo, entre instrucción e instrucción, pasan más ciclos de lo normal :-).
Conmutación entre tareas
Como se comentó más arriba, cuando se produce una interrupción, los procesadores guardan siempre en la pila la dirección a donde el contador de programa (PC) debe regresar una vez que la interrupción ha terminado de servirse (cuando la ISR termine de ejecutarse). En el caso del ATmega32U4 el procesador empuja en la pila 3 bytes en dos de los cuales almacena la dirección de memoria de la siguiente instrucción que iba a ejecutar (aunque el ATmega32U4 tiene un espacio de direccionamiento de 16 bits, el núcleo AVR que utiliza es el mismo que tienen otros procesadores AVR que tienen un espacio de direcciones de más de 16 bits, de ahí los 3 bytes que se reservan en la pila para la dirección de retorno de la interrupción).
Si lo que queremos es conmutar entre tareas lo que hay que hacer nada más empezar la ejecución de la función ISR es guardar absolutamente todo el estado del procesador y esto se consigue en el caso de AVR apilando los 32 registros generales (desde R0 hasta R31) más el registro de estado SREG en la pila del sistema (PUSH).
ISR(TIMER0_OVF_vect) __attribute__ ((naked)); ISR(TIMER0_OVF_vect) { asm volatile ( "push r0\n" "push r1\n" "push r2\n" "push r3\n" "push r4\n" "push r5\n" "push r6\n" "push r7\n" "push r8\n" "push r9\n" "push r10\n" "push r11\n" "push r12\n" "push r13\n" "push r14\n" "push r15\n" "push r16\n" "push r17\n" "push r18\n" "push r19\n" "push r20\n" "push r21\n" "push r22\n" "push r23\n" "push r24\n" "push r25\n" "push r26\n" "push r27\n" "push r28\n" "push r29\n" "push r30\n" "push r31\n" "in r0, 0x3f\n" "push r0\n"
A continuación, y como el top de la pila es algo cambiante a medida que se va ejecutando código, guardamos en una variable global la dirección de memoria del actual top de la pila: esto nos permitirá acceder cómodamente a los registros que acabamos de guardar independientemente de que empujemos más cosas en ella:
// update stackPointerReference "push r0\n" "in r0, 0x3e\n" "sts stackPointerReference + 1, r0\n" // sph "in r0, 0x3d\n" "sts stackPointerReference, r0\n" // spl "pop r0\n" ); stackPointerReference = (volatile uint8_t *) ((((uint32_t) stackPointerReference) + 1) | 0x800000); // 23-th bit to 1 for SRAM address space
Poner a 1 el bit 23 del puntero stackPointerReference es un artificio necesario en avr-gcc ya que en ese entorno de compilación esa es la forma en la que se diferencian los punteros a memoria de datos de los punteros a memoria de programa (hay que recordar que los AVR tienen arquitectura Harvard).
Tras tener adecuadamente inicializado el puntero "stackPointerReference" podemos proceder a realizar la conmutación de tareas en sí. En nuestro caso se asume una política de tipo Round-robin en la que todas las tareas tienen exactamente el mismo tiempo de proceso. Lo que haremos será, partiendo de una lista de N tareas, cada vez que se ejecute la interrupción de desbordamiento del Timer 0, cambiaremos de la tarea i-ésima a la tarea ((i + 1) MOD N)-ésima, con lo que nos aseguramos que cuando llegamos a la última tarea de la lista volvemos a empezar por la primera y así sucesivamente.
Para cada tarea definimos un objeto de clase Task:
class StackFrame { public: uint8_t sreg; uint8_t r[32]; uint8_t pc[3]; void setPC(void *f) { this->pc[0] = 0; this->pc[1] = ((uint32_t) f) & 0x000000FF; this->pc[2] = ((((uint32_t) f) >> 8) & 0x000000FF); }; } __attribute__ ((packed)); class Task { public: StackFrame stackFrame; bool started; void (*run)(); Task() : started(false) { }; };
Cada tarea tiene una copia del marco de pila ("stack frame") de la última vez que fue interrumpida, un booleano para indicar si la tarea ha sido iniciada o no y un puntero a una función que apunta a la primera instrucción de dicha tarea. En nuestro caso vamos a asumir, sin pérdida de generalidad, que nuestras tareas nunca terminan (no vamos a controlar lo que ocurre cuando la tarea termine).
Definimos además de forma global un array de punteros a objetos de tipo Task, una variable "currentTaskIndex" que indica la actual tarea que está en ejecución y el puntero "stackPointerReference" del que hablamos antes.
const uint16_t MAX_TASKS = 4; volatile uint16_t numTasks; volatile Task tasks[MAX_TASKS]; volatile uint16_t currentTaskIndex; volatile uint8_t *stackPointerReference;
Los primero que hacemos tras calcular el valor de "stackPointerReference" es trabajar con la tarea actual:
Task *currentTask = (Task *) &tasks[currentTaskIndex]; if (currentTask->started) { // copy stack data to currentTask->stackFrame memcpy((void *) ¤tTask->stackFrame, (const void *) (stackPointerReference + 1), sizeof(StackFrame)); } else { // replace return address on currentTask->data with currentTask->run memset((void *) ¤tTask->stackFrame, 0, sizeof(StackFrame)); currentTask->stackFrame.setPC((void *) currentTask->run); }
Si ya está iniciada copiamos los registros que acabamos de apilar (en los PUSH masivos que hicimos al principio de la ISR) al campo "stackFrame" del objeto Task correspondiente a la tarea actual: esto es, ponemos a salvo los registros de la tarea actual pues nos disponemos a hacer una conmutación a la siguiente tarea.
En caso de que la tarea actual no esté iniciada lo que hacemos es borrar el campo "stackFrame" del objeto Task correspondiente a la tarea actual e inicializamos, dentro de esta estructura "stackFrame", los bytes correspondientes al contador de programa para que apunten a la primera instrucción de la tarea actual. Esto hará que cuando se restaure el marco de pila ("stack frame") de esta tarea se inicie dicha tarea (puesto que el contador de programa irá a la primera instrucción de dicha tarea).
A continuación trabajamos con el objeto de tipo Task correspondiente a la tarea siguiente:
uint16_t nextTaskIndex = currentTaskIndex + 1; if (nextTaskIndex == numTasks) nextTaskIndex = 0; Task *nextTask = (Task *) &tasks[nextTaskIndex]; if (nextTask->started) { // replace stack data with nextTask->stackFrame memcpy((void *) (stackPointerReference + 1), (const void *) &nextTask->stackFrame, sizeof(StackFrame)); } else { // replace return address on stack with nextTask->run ((StackFrame *) (stackPointerReference + 1))->setPC((void *) nextTask->run); nextTask->started = true; }
En caso de que la siguiente tarea a iniciar ya esté iniciada ("started") simplemente sobreescribimos todo el marco de pila (los datos que metimos en la pila con los PUSH masivos del principio de la ISR) con los bytes de campo "stackFrame" de la siguiente tarea, lo que provocará una conmutación a la tarea siguiente en el momento que retornemos de la interrupción. En caso de que la siguiente tarea no esté iniciada aún hacemos lo mismo que en caso de la tarea actual: inicializamos, dentro de la estructura "stackFrame" los bytes correspondientes al contador de programa para que apunten a la primera instrucción de la tarea siguiente y, a continuación, marcamos la tarea como iniciada ("started = true").
Antes de terminar actualizamos la variable global "currentTaskIndex" para que apunte a la tarea a la que se le va a entregar el control de la CPU y hacemos una restauración normal de la pila (POP masivos) antes de terminar definitivamente con la instrucción "RETI".
currentTaskIndex = nextTaskIndex; asm volatile ( "pop r0\n" "out 0x3f, r0\n" "pop r31\n" "pop r30\n" "pop r29\n" "pop r28\n" "pop r27\n" "pop r26\n" "pop r25\n" "pop r24\n" "pop r23\n" "pop r22\n" "pop r21\n" "pop r20\n" "pop r19\n" "pop r18\n" "pop r17\n" "pop r16\n" "pop r15\n" "pop r14\n" "pop r13\n" "pop r12\n" "pop r11\n" "pop r10\n" "pop r9\n" "pop r8\n" "pop r7\n" "pop r6\n" "pop r5\n" "pop r4\n" "pop r3\n" "pop r2\n" "pop r1\n" "pop r0\n" "reti\n" ); }
Para la prueba de concepto se implementaros dos tareas muy sencillas: cada una hace parpadear un led a una velocidad diferente:
void task1() __attribute__ ((naked)); void task1() { DDRD |= 0x04; // PD2 (D0 on Arduino Leonardo) as output while (true) { PORTD ^= 0x04; for (volatile uint32_t i = 0; i < 66000; i++) ; } } void task2() __attribute__ ((naked)); void task2() { DDRC |= 0x80; // PC7 (D13 on Arduino Leonardo) as output while (true) { PORTC ^= 0x80; for (volatile uint32_t i = 0; i < 200000; i++) ; } }
Consideraciones adicionales
Nótese que tanto la ISR como las funciones "tarea" ("task1" y "task2") son declaradas con el atributo "naked". Este atributo indica al compilador que no genere código preámbulo ni postámbulo (el código ensamblador relacionado normalmente con el manejo de parámetros y valores de retorno).
En el caso de las funciones "task1" y "task2" se ha usado este atributo por una cuestión de coherencia ya que no se trata de funciones que son invocadas de forma normal desde otra parte del programa y además se trata de funciones que no terminan nunca de ejecutarse.
El caso de la función ISR es más delicado porque en ese caso sí que es necesario usar el atributo "naked". Como se vió en la primera prueba con la interrupción del Timer 0, para el siguiente código:
ISR(TIMER0_OVF_vect) {
PORTC ^= 0x80;
}
El compilador generaba instrucciones PUSH y POP de los registros que utilizaría, antes y después de la operación "PORTC ^= 0x80" respectivamente. En nuestro caso necesitamos que el apilado (PUSH) y desapilado (POP) de registros sea siempre igual y masivo y que esté perfectamente controlado por nosotros por lo que definimos la función con el atributo "naked" y nos encargamos nosotros de escribir de forma explícita el código ensamblador de preámbulo y postámbulo de la ISR.
Todo el código puede descargarse de la sección soft.
[ añadir comentario ] ( 7613 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 6167 )
( 3 / 6167 )El efecto "shuffle" o "swing" es un efecto muy utilizado en producción musical para humanizar y meter mas "groove" a canciones reproducidas por un secuenciador. El efecto consiste básicamente en adelantar o atrasar el disparo de determinadas notas durante algunos milisegundos para dar sensación de "humanidad" a la cadencia de la música. A lo largo de este post se abordará la implementación en C++ sobre Arduino de un "shuffler" MIDI para secuencias 4/4.
La forma más estándar de "shuffle" en secuencias musicales de 4/4 es la que consiste en retrasar una cantidad de tiempo determinada (milisegundos) la segunda y la cuarta semicorchea después de cada negra:
*----.----.----.----*----.----.----.----*----.----.----.----*----.----.----.---- Compás 4/4 estándar
*------.--.------.--*------.--.------.--*------.--.------.--*------.--.------.-- Compás de 4/4 con "shuffle"
Los asteriscos determinan las negras (4 negras por cada compás de 4/4) y los puntos determinan las semicorcheas (4 semicorcheas por cada negra). El concepto es muy sencillo, aunque a la hora de implementarlo en MIDI hay que tener en cuenta algunos aspectos importantes.
Protocolo MIDI
El protocolo MIDI es un protocolo muy sencillo por el que se envían eventos e información musical. No es objetivo de este post el explicar el protocolo ni los mensajes MIDI (cualquier búsqueda sobre "midi protocol" en la red nos dará acceso a centenares de páginas donde lo explican muy bien) aunque sí nos centraremos en los mensajes que más nos interesan de cara a implementar nuestro shuffler.
Dentro de los mensajes MIDI hay unos especiales denominados de tiempo real que son transmitidos por los secuenciadores cuando están reproduciendo una secuencia MIDI pregrabada:
0xF8: "timing clock" se envía 24 veces por cada negra.
0xFA: "start" indica que se va a iniciar la reproducción de una secuencia. Este mensaje es seguido de forma inmediata por el primer 0xF8.
0xFB: "continue" indica que se reanuda la secuencia por donde se paró.
0xFC: "stop" indica que se para la secuencia.
Por tanto, si en nuestro secuenciador musical tenemos una canción con un tempo de 120 negras por minuto, al emitir dicha secuencia por un cable MIDI, de forma intercalada con los mensaje de activación y desactivación de las notas y demás, irán entremezclados mensajes 0xF8 a razón de 24 por cada negra, es decir:
$${{120 \times 24} \over 60} = 48\;mensajes/segundo$$
Nótese que la cantidad de mensajes 0xF8 enviados por unidad de tiempo no depende de la velocidad de transmisión MIDI, sino del tempo de la secuencia musical que se esté reproduciendo. Si cada vez que nos llegue un mensaje 0xF8 desde el secuenciador vamos contando de 0 a 23 dando la vuelta de nuevo a 0 cada vez que llegamos a 24 tenemos que los mensaje 0xF8 coinciden en el tiempo con las negras y semicorcheas de la forma que indica la siguiente tabla:
n s s s
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
En esta tabla se puede ver que la negra (el beat) coincide con el contador de mensajes 0xF8 recibidos a 0 mientras que las tres semicorcheas siguientes coinciden con ese mismo contador a 6, a 12 y a 18. Ahora tenemos una base de tiempo sólida que podemos aprovechar para implementar nuestro efecto shuffle: Lo que hay que hacer es atrasar en el tiempo los mensajes de "note on" y "note off" que lleguen entre el instante 6 y el 12 y entre el instante 18 y 0 de la siguiente negra.
n s s s
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
+--------> atrasar +--------> atrasar
Dicho atraso no puede ser tal que nuestro shuffler emita notas fuera de orden por lo que el retraso en el tiempo debe ser proporcional (una nota que llegue entre los instantes 6 y el 7 será atrasada más que una que llegue entre los instantes 9 y 10 pero la primera nunca debe emitirse depués de la segunda, debemos garantizar el orden de llegada de los eventos "note on" y "note off").
Algoritmo propuesto
El MIDI shuffler se plantea como un filtro MIDI, un dispositivo con una entrada MIDI y una salida MIDI que se intercala entre el secuenciador y los sintetizadores. La salida MIDI del secuenciador irá conectada a la entrada MIDI del shuffler y la salida MIDI del shuffler irá conectada a la entrada MIDI de los secuenciadores. A continuación se plantea una propuesta de pseudocódigo para el MIDI shuffler:
iniciarShuffler
estado := ESPERAR_START_MIDI
fin iniciarShuffler
getInstanteAtrasado(t)
ret := (tamSemicorchea - tamReducido) + ((t + tamReducido) / tamSemicorchea)
devolver ret
fin getInstanteAtrasado
byteMIDIRecibido(byte)
enviar := SÍ
si (estado = ESPERAR_START_MIDI) entonces
si (byte = 0xFA) entonces
colaRetraso.borrar()
estado := ESPERAR_PRIMER_CLOCK_MIDI
fin sin
en otro caso, si (estado = ESPERAR_PRIMER_CLOCK_MIDI) entonces
si (byte = 0xF8) entonces
estado := ESPERAR_CLOCK_MIDI
contadorReloj := 6
indiceSemicorchea := 0
timer.iniciar()
fin si
en otro caso, si (estado = ESPERAR_CLOCK_MIDI) entonces
si (byte = 0xF8) entonces
contadorReloj := contadorReloj - 1
si (contadorReloj = 0) entonces
si ((indiceSemicorchea = 0) ó (indiceSemicorchea = 2)) entonces
tamSemicorchea = timer.getValor()
tamReducido = (temSemicorchea * (100 - PERCENT)) / 100
fin si
contadorReloj := 6
indiceSemicorchea := (indiceSemicorchea + 1) mod 4
timer.parar()
timer.iniciar()
fin si
en otro caso, si (esEventoNota(byte) y ((indiceSemicorchea = 1) ó (indiceSemicorchea = 3)) entonces
t := getInstanteAtrasado(timer.getValor())
colaRetraso.meter({byte, t})
enviar := NO
en otro caso, si (byte = 0xFC)
estado := ESPERAR_START_MIDI
fin si
fin si
si (enviar = SÍ) entonces
enviar(byte)
fin si
fin byteMIDIRecibido
principal
siempre hacer
si ((indiceSemicorchea = 1) ó (indiceSemicorchea = 3)) entonces
t := timer.getValor()
mientras (colaRetraso.hayAlgo()) hacer
d := colaRetraso.getCabeza()
si (d.t <= t) entonces
colaRetraso.sacar()
enviar(d.byte)
en otro caso
salir del bucle
fin si
fin mientras
fin si
fin siempre
fin principal
Lo que hace el algoritmo es aprovechar el intervalo entre el midi clock 0 y el 5 para calcular el tiempo en unidades de timer que dura una semicorchea. El objeto "timer" es un timer de bastante resolución que se arranca en el instante 0 y se para en el instante 6. En ese instante 6, una vez parado el timer, se anota la cuenta del mismo como tamSemicorchea (para indicar que es el tamaño en ticks de nuestro contador de lo que dura una semicorchea) y se calcula tamReducido a partir del porcentaje de "shuffle" que queramos (un shuffle del 0% da un tamReducido = tamSemicorchea, mientras que un shuffle del 100% da un tamReducido = 0).
instante semicorchea acción
0 0 Iniciar timer de alta resolución
1
2
3
4
5
6 1 Anotar cuenta del timer, pararlo
7 y volver a iniciarlo. Encolar cualquier
8 evento "note on" o "note off" que llegue
9 en este intervalo calculando su instante
10 de emisión con una regla de tres.
11
12 2 La misma que la semicorchea 0
13
14
15
16
17
18 3 La misma que la semicorchea 1
19
20
21
22
23
Entre los instantes 6 y el 11 lo que se hace es encolar los eventos de "note on" y "note off" que vayan llegando calculándoles en el momento que llegan, en qué instante del tick del timer deben ser transmitidos haciendo una regla de tres (en getInstanteAtrasado) y metiendo cada una de estas parejas de valores (byte e instante que debe ser transmitido) en la cola "colaRetraso".
Lo mismo se hace para los instantes de tiempo 12 al 17 y 18 al 23, respectivamente.
Ya tenemos los eventos atrasados metidos en una cola (para garantizar que el orden de emisión sea el mismo que el de recepción), ahora lo que hay que hacer es emitirlos en el instante que corresponda. y de esto se encarga el procedimiento principal en su bucle infinito. Este procedimiento principal ejecuta un bucle infinito que lo que hace es inspeccionar si hay algo que enviar en la cola "colaRetraso", si hay algo que debe ser enviado (su instante de envío es menor o igual al valor actual del timer) lo envía y lo quita de la cola. El procedimiente byteMIDIRecibido es invocado cada vez que llega un byte por el puerto MIDI.
El circuito
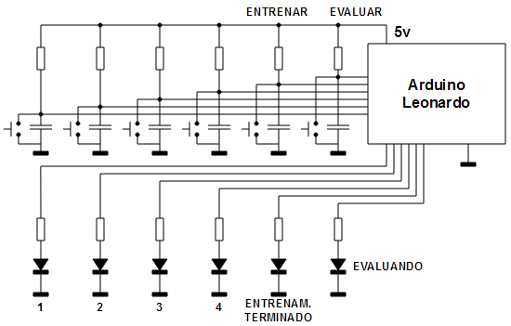
El MIDI shuffler, como se comentó antes, hace de filtro MIDI con una entrada y una salida. La cantidad de efecto shuffle se controla mediante un potenciómetro conectado a una de las entradas analógicas del Arduino.
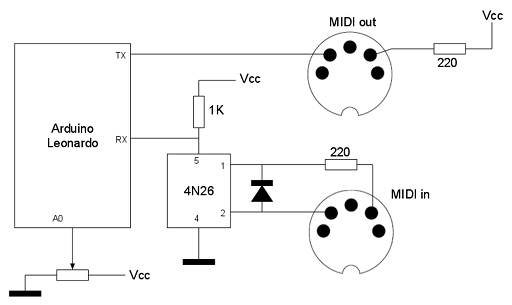
Con el potenciómetro al mínimo se aplica un efecto shuffle del 0% (sin efecto shuffle) mientras que con el potenciómetro al máximo se aplica un efecto shuffle del 50% (valores superiores al 50% genera unos resultados muy extremos).
Implementación en C++
A pesar de que en el algoritmo propuesto el procedimiento byteMIDIRecibido se supone que es invocado de forma asíncrona por el sistema cada vez que llega un byte por el puerto MIDI, lo cierto es que es más sencillo si en la rutina de interrupción de la UART encolamos los bytes MIDI que van llegando por la entrada MIDI y luego los vamos sirviendo en el bucle principal antes de comprobar el estado de la colaRetraso, haciéndolo de esta forma evitamos colisiones y la necesidad de hacer que colaRetraso sea reentrante.
int32_t MIDIShuffler::getDelayedInstant(int32_t sourceInstant) { return ((this->sixteenthNoteLength - this->reducedLength) + ((sourceInstant * this->reducedLength) / this->sixteenthNoteLength)); } void MIDIShuffler::byteReceived(uint8_t byte) { this->rxQueue.push(byte); } void MIDIShuffler::processRxByte(uint8_t byte) { bool send = true; uint8_t noChannelByte = byte & 0xF0; if (this->status == STATUS_WAIT_START_MIDI_CLOCK) { if (byte == 0xFA) { this->delayQueue.clear(); this->rxQueue.clear(); this->status = STATUS_WAIT_FIRST_MIDI_CLOCK; } } else if (this->status == STATUS_WAIT_FIRST_MIDI_CLOCK) { if (byte == 0xF8) { this->status = STATUS_WAIT_MIDI_CLOCK; this->clockCounter = CLOCK_PER_SIXTEENTH_NOTE; this->sixteenthNoteIndex = 0; this->timeCounter->start(); } } else if (this->status == STATUS_WAIT_MIDI_CLOCK) { if (byte == 0xF8) { this->clockCounter--; if (this->clockCounter == 0) { if ((this->sixteenthNoteIndex == 0) || (this->sixteenthNoteIndex == 2)) { this->sixteenthNoteLength = this->timeCounter->getValue(); this->reducedLength = (this->sixteenthNoteLength * (100 - this->percentProvider->getPercent())) / 100; } this->clockCounter = CLOCK_PER_SIXTEENTH_NOTE; this->sixteenthNoteIndex = (this->sixteenthNoteIndex + 1) & 3; // ... % 4 this->timeCounter->stop(); this->timeCounter->start(); } } else if ((noChannelByte < 0xA0) && ((this->sixteenthNoteIndex == 1) || (this->sixteenthNoteIndex == 3)) && !this->byPass) { DelayedMIDIByte d(this->getDelayedInstant(this->timeCounter->getValue()), byte); this->delayQueue.push(d); send = false; } else if (byte == 0xFC) this->status = STATUS_WAIT_START_MIDI_CLOCK; } if (send && (this->sender != NULL)) this->sender->sendByte(byte); } void MIDIShuffler::init(MIDISender &sender, PercentProvider &percentProvider, TimeCounter &timeCounter) { MIDIFilter::init(sender); this->percentProvider = &percentProvider; this->delayQueue.clear(); this->rxQueue.clear(); this->status = STATUS_WAIT_START_MIDI_CLOCK; this->timeCounter = &timeCounter; this->byPass = false; this->sixteenthNoteIndex = 0; } void MIDIShuffler::run() { if (this->rxQueue.hasElements()) { uint8_t byte = this->rxQueue.getHead(); this->processRxByte(byte); this->rxQueue.pop(); } if (((this->sixteenthNoteIndex == 1) || (this->sixteenthNoteIndex == 3)) && this->delayQueue.hasElements()) { int32_t t = this->timeCounter->getValue(); while (this->delayQueue.hasElements()) { DelayedMIDIByte d = this->delayQueue.getHead(); if (d.t <= t) { this->delayQueue.pop(); if (this->sender != NULL) this->sender->sendByte(d.byte); } else break; } } }
A continuación puede verse un vídeo con el MIDI shuffler en acción (obviamente, hay que poner el audio para que se oiga :-) )
Todo el código fuente puede descargarse de la sección soft.
[ añadir comentario ] ( 3114 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 15731 )
( 3 / 15731 )Las redes neuronales son un tópico que se ha vuelto a poner de moda gracias al concepto del "deep learning" y a la irrupción de las redes neuronales convolucionales, que han revolucionado, sobre todo, las técnicas de reconocimiento de imágenes. No vamos a llegar tan lejos: implementaremos un sencillo perceptrón multicapa (MLP) en un Arduino que permita a este aprender y predecir el comportamiento de un usuario que acciona unos botones. No es un juego especialmente entretenido pero sirve como prueba de concepto de la implementación de redes neuronales artificiales sobre sistemas embebidos.
Perceptrón multicapa (MLP)
En un post anterior se explicaron los fundamentos teóricos de los perceptrones multicapa. Tenemos un conjunto de neuronas dispuestas en cascada, las de un extremo son las neuronas de entrada y las del otro extremo son las neuronas de salida.
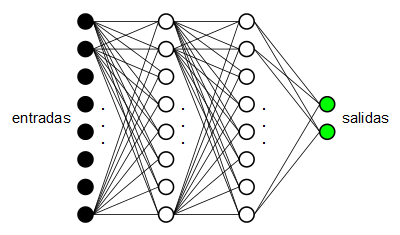
Cada capa de neuronas está conectada con la capa inmediatamente anterior mediante un conjunto de pesos sinápticos que determinan el nivel de influencia de cada neurona de la capa (i-1)-ésima con cada neurona de la capa i-ésima. Los valores de entrada pasan por la matriz de pesos sinápticos que une la capa de entrada con la primera capa intermedia y determinan los valores de las neuronas de la primera capa oculta, a continuación este primera capa oculta propaga sus valores a través de otra matriz de pesos que une dicha capa con la siguiente y así sucesivamente hasta llegar a la capa de salida. La salida del perceptrón multicapa serán las salidas de las neuronas de la última capa.
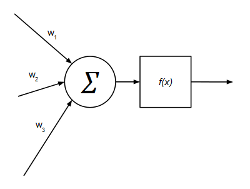
La salida de cada neurona oculta y de salida viene determinada por:
$$suma^{o}_{pk} = \sum_{j=1}^{L}w_{kj}^{o}y_{pj} + \theta_{k}^{o}$$
$$y_{pk}=f_{k}^{o}(suma^{o}_{pk})$$
Siendo:
$w_{kj}^{o}$ el peso sináptico de la neurona $j$ de la capa anterior sobre la neurona $k$ de la capa actual.
$f$ la función de activación (en este caso la sigmoide).
$$f(x) = {{1} \over {1+e^{-x}}}$$
Cada neurona puede representarse de forma gráfica de la siguiente manera:
Por ejemplo, un perceptrón multicapa con 6 entradas, 2 salidas y una capa ocultas con 4 neuronas tendrá la siguiente configuración:
A0 = {a01, a02, a03, a04, a05, a06} <-- capa de entrada
W0,1 = { <-- pesos sinápticos entre la entrada y la capa oculta
w11 w12 w13 w14 w15 w16
w21 w22 w23 w24 w25 w26
w31 w32 w33 w34 w35 w36
w41 w42 w43 w44 w45 w46
}
A1 = {a11 a12 a13 a14} <-- capa oculta
X1,2 = { <-- pesos sinápticos entre la capa oculta y la salida
x11 x12 x13 x14
x21 x22 x23 x24
}
A2 = {a21 a22} <-- capa de salidaRecomiendo leer el post anterior donde se explica de forma más pormenorizada tanto el perceptrón multicapa como el algoritmo de aprendizaje "backpropagation", el más utilizado y el usado en esta prueba de concepto.
Juego de predicción
Se plantea un sencillo juego de predicción en el que el Arduino deberá aprenderse los movimientos del usuario que interactúa con él. Se disponen 4 pulsadores y 4 leds (a cada led le corresponde un botón y viceversa). Se incluyen además dos pulsadores adicionales etiquetados como "ENTRENAR" y "EVALUAR" y dos leds adicionales etiquetados como "ENTRENAMIENTO TERMINADO" y "EVALUANDO". Se implementa una red neuronal de tipo MLP con 8 entradas, una capa oculta de 8 neuronas y una capa de salida de 4 neuronas. 4 de las neuronas de entrada recogen las entradas de los 4 pulsadores (1 = pulsado, 0 = no pulsado) y las 4 neuronas de entrada restantes reciben el valor de los pulsadores del instante anterior (es una forma de dar memoria a la red), las cuatro neuronas de salida están conectadas a los 4 leds de salida (encendido = salida de la neurona mayor que 0.5, apagado = en caso contrario).
En modo evaluación el Arduino cada vez que detecta la pulsación de un botón aplica los valores correspondientes a las 8 neuronas de entrada, evalúa el MLP y emite el valor de las 4 neuronas de salida a los leds. En modo entrenamiento la red se va entrenando a sí misma observando las pulsaciones del usuario. La mecánica del "juego" es la siguiente:
1. Nada más arrancar el Arduino, inicia en modo EVALUACIÓN e ilumina el led "EVALUANDO". En este modo cada vez que se pulsa uno de los 4 pulsadores de entrada se evalúa la red neuronal y se emite la salida correspondiente. Como inicialmente los pesos sinápticos son aleatorios, los leds actuarán de forma aleatoria en función de la entrada.
2. Cuando queramos entrenar la red neuronal, pulsamos "ENTRENAR". Esto hace que el led "EVALUANDO" se apague para indicar que estamos en modo aprendizaje y la red entra en modo de aprendizaje. El usuario empieza a accionar los pulsadores en el orden que quiera, se asume una secuencia de cuatro pulsaciones de tal manera que cada cuatro pulsaciones, la red es entrenada para que sea capaz de aprenderse la secuencia. Cada vez que terminamos de introducir una secuencia (cuatro pulsaciones), la red es entrenada con la secuencia introducida y se ilumina el led "ENTRENAMIENTO TERMINADO", si seguimos repitiendo la secuencia afianzaremos el aprendizaje de la red neuronal.
3. Una vez que el led "ENTRENAMIENTO TERMINADO" se haya iluminado al menos una vez podemos volver al modo de evaluación accionando el pulsador "EVALUAR". Al entrar de nuevo en el modo de evaluación se iluminará el led "EVALUANDO". Tras el entrenamiento la red tendrá los pesos sinápticos modificados por el aprendizaje de tal manera que intentará predecir qué pulsador accionará el jugador en cada momento.
Veamos un ejemplo:
1. Encendemos y esperamos a que se encienda el led "EVALUANDO". Comprobamos que al accionar cualquiera de los 4 pulsadores los leds de salida se encienden y se apagan sin criterio, de forma aleatoria debido a los pesos sinápticos aleatorios.
2. Pulsamos "ENTRENAR" y esperamos a que se apague el led "EVALUANDO". Ahora estamos en modo aprendizaje (o entrenamiento).
3. Nos inventamos una secuencia, por ejemplo {1, 4, 2, 3} y vamos accionando los pulsadores de entrada en ese orden. Cuando pulsemos el último número de la secuencia, el 3, se aplicará el algoritmo de aprendizaje para entrenar la red neuronal y una vez termine, se encenderá el led "ENTRENAMIENTO TERMINADO".
4. Llegamos a este punto podemos seguir entrenando la red con la misma secuencia (volvemos a introducir la secuencia en orden {1, 4, 2, 3}, al pulsar el 1 se apagará el led "ENTRENAMIENTO TERMINADO" y volverá a encenderse cuando pulsemos el 3 para indicar que se ha realizado otro entrenamiento) o podemos pasar al modo de evaluación.
5. Para pasar al modo de evaluación pulsamos "EVALUAR". Esto hará que el led "EVALUANDO" se encienda y ahora podremos probar la red entrenada.
6. En modo evaluación lo que hace la red es tratar de adivinar qué pulsador se accionará en el siguiente movimiento. Por ejemplo en nuestro caso, para la secuencia {1, 4, 2, 3}, ocurrirá lo siguiente:
pulsamos 1 --> se enciende el 4
pulsamos 4 --> se enciende el 2
pulsamos 2 --> se enciende el 3
pulsamos 3 --> se enciende el 1
Como se puede comprobar, la red neuronal se ha aprendido nuestros movimientos correctamente.
Implementación
A continuación puede verse el diagrama de clases utilizado en la implementación del juego de predicción en C++:
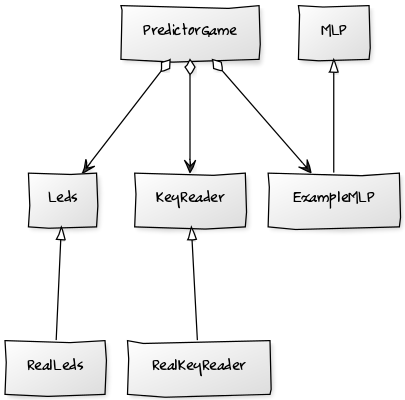
Se trata de una estructura de código muy sencilla. La clase PredictorGame mantiene la máquina de estados principal del juego, lee los pulsadores, controla las luces e incluye también la red neuronal (ExampleMLP). La clase MLP es una clase abstracta que permite definir mediante la implementación de varios de sus métodos virtuales puros la topología de un perceptrón multicapa cualquiera (entradas, capas ocultas y neuronas de salida). La clase ExampleMLP es una especialización de MLP con la topología descrita: 8 entradas, 1 capa intermedia oculta con 8 neuronas y una capa de salida de 4 neuronas.
#include <time.h> #include <math.h> #include <stdlib.h> #include "MultilayerPerceptron.H" using namespace avelino; using namespace std; float MultilayerPerceptron::getNetValue(uint8_t numNeuronsPrevLayer, uint8_t currentLayer, uint8_t n) { float acc = 0; for (uint8_t p = 0; p < numNeuronsPrevLayer; p++) { float x = this->getNeuronValue(currentLayer - 1, p); float w = this->getInputWeight(currentLayer, p, n); acc = acc + (x * w); } return acc; } void MultilayerPerceptron::evaluate() { uint8_t numLayers = this->getNumHiddenLayers() + 1; for (uint8_t l = 1; l <= numLayers; l++) { uint8_t numNeurons = this->getNumNeurons(l); uint8_t numNeuronsPrevLayer = this->getNumNeurons(l - 1); for (uint8_t n = 0; n < numNeurons; n++) { float acc = this->getNetValue(numNeuronsPrevLayer, l, n); float y = 1.0 / (1.0 + exp(-acc)); this->setNeuronValue(l, n, y); } } } void MultilayerPerceptron::setTrainRate(float r) { this->trainRate = r; } float MultilayerPerceptron::getTrainRate() { return this->trainRate; } float MultilayerPerceptron::getEstimatedError(uint8_t layer, uint8_t n) { uint8_t numLayers = this->getNumHiddenLayers() + 1; float ret = 0; if (layer == numLayers) { float out = this->getNeuronValue(layer, n); ret = (this->getDesiredOutput(n) - out); } else { uint8_t numNeuronsNextLayer = this->getNumNeurons(layer + 1); for (uint8_t k = 0; k < numNeuronsNextLayer; k++) { float e = this->getNeuronErrorValue(layer + 1, k); float w = this->getInputWeight(layer + 1, n, k); ret += (e * w); } } return ret; } void MultilayerPerceptron::backpropagate(uint8_t layer, float *totalError) { if (totalError != NULL) *totalError = 0; uint8_t numNeurons = this->getNumNeurons(layer); for (uint8_t n = 0; n < numNeurons; n++) { float out = this->getNeuronValue(layer, n); float aux = out * (1 - out); float error = aux * this->getEstimatedError(layer, n); this->setNeuronErrorValue(layer, n, error); if (totalError != NULL) *totalError += (error * error); } uint8_t numNeuronsPrevLayer = this->getNumNeurons(layer - 1); for (uint8_t n = 0; n < numNeurons; n++) { float e = this->getNeuronErrorValue(layer, n); for (uint8_t k = 0; k < numNeuronsPrevLayer; k++) { float y = this->getNeuronValue(layer - 1, k); float w = this->getInputWeight(layer, k, n); w = w + (this->trainRate * e * y); this->setInputWeight(layer, k, n, w); } } } void MultilayerPerceptron::train(uint8_t times, float &totalError) { while (times > 0) { uint8_t outputLayer = this->getNumHiddenLayers() + 1; for (uint8_t l = outputLayer; l >= 1; l--) { float *e = (l == outputLayer) ? &totalError : NULL; this->backpropagate(l, e); } this->commitInputWeights(); times--; } } void MultilayerPerceptron::initWithRandomWeights() { srand(time(NULL)); uint8_t n = this->getNumHiddenLayers() + 1; for (uint8_t l = 1; l <= n; l++) { uint8_t prevLayerNumNeurons = this->getNumNeurons(l - 1); uint8_t currentLayerNumNeurons = this->getNumNeurons(l); for (uint8_t from = 0; from < prevLayerNumNeurons; from++) { for (uint8_t to = 0; to < currentLayerNumNeurons; to++) { float v = ((2.0f * rand()) / RAND_MAX) - 1.0f; this->setInputWeight(l, from, to, v); } } } this->commitInputWeights(); } void MultilayerPerceptron::setMaxError(float v) { this->maxError = v; } float MultilayerPerceptron::getMaxError() { return this->maxError; }
El código fuente está organizado de tal manera que el que es independiente de la plataforma (clases MultilayerPerceptron, ExampleMultilayerPerceptron, KeyReader, Leds y PredictorGame) se encuentra en la carpeta raiz. El código dependiente de cada plataforma se encuentra en la carpeta correspondiente a dicha plataforma: dentro de la carpeta "linux" están las clases "LinuxKeyReader" y "LinuxLeds" así como el fichero "main.cc" para Linux y dentro de la carpeta "arduino" están las clases "RealKeyReader" y "RealLeds" así como el fichero "main.cc" para Arduino. En este caso concreto, las clases "RealKeyReader" y "RealLeds" están especializadas para el patillaje del Arduino Leonardo pero son fácilmente adaptables a otros modelos de Arduino.
Para compilar la versión "linux" basta con entrar en la carpeta "linux" y hacer "make" mientras que para compilar la versión "arduino" hay que ir a la carpeta "arduino", editar el fichero "Makefile", poner los valores adecuados para la carpeta donde está instalado el IDE de Arduino ("ARDUINO_FOLDER") y el puerto serie donde se conecta el Arduino ("SERIAL") y a continuación hacer "make" para generar el fichero "main.hex" y "make install" para tostarlo en el Arduino.
A nivel eléctrico se trata de un circuito sumamente sencillo: 6 pulsadores, con su pequeña red antirrebote cada uno, y 6 leds.
Todo el código está disponible en la sección soft.
[ añadir comentario ] ( 2935 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 6994 )
( 3 / 6994 )Las FPGAs y los CPLDs son circuitos integrados digitales programables a nivel hardware mediante algún tipo de lenguaje de descripción de hardware (VHDL, Verilog, SystemC, etc.). A lo largo de este post se desarrolla una primera toma de contacto con este tipo de integrados.
FPGA
La FPGA que se ha usado es una Xilinx Spartan 3E, que se puede encontrar en la placa Papilio One (http://papilio.cc). Esta placa es open hardware, con interface USB, memoria flash SPI para almacenar la configuración del hardware y con una buena relación calidad/precio (unos 38 dólares aproximadamente).
El entorno de desarrollo de Xilinx es un poco complejo (muchas opciones) pero se le coge el truco rápido. Es gratuito (aunque no es software libre) y muy fácil de instalar tanto en Windows como en Linux (no está para Mac). El entorno de desarrollo permite gestionar proyectos en VHDL o Verilog y generar al final los ficheros ".bit" que son los que se mandan a la FPGA.
De http://papilio.cc se descarga el Papilio Loader, un software open source que permite "tostar" los ficheros ".bit" en la placa FPGA y probar los diseños rápidamente. En la propia página del proyecto vienen varios tutoriales.
Prueba de concepto
Como prueba inicial se plantea un circuito conversor de binario (4 bits, del 0 al 9) a 7 segmentos mediante interfaz serie:
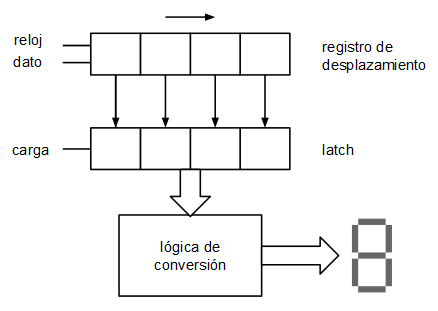
Se trata de un esquema muy sencillo: un registro de desplazamiento de 4 bits (que permite leer la entrada serie), un latch de 4 bits que carga el contenido del registro de desplazamiento y a la salida del latch una lógica combinatoria que convierte el número de 4 bits en una salida de 7 bits (para el display de 7 segmentos).
VHDL de la lógica combinatoria
VHDL es un lenguaje de descripción de hardware, no un lenguaje imperativo al uso. Cada línea de código describe un comportamiento y la única forma de realizar procesamiento secuencial es mediante la cláusula "process" ya que por defecto se ejecuta "todo a la vez".
Una lógica combinatoria está basada en puertas lógicas y las puertas lógicas se "ejecutan" siempre, no son como los biestables u otros elementos secuenciales. Para la lógica combinatoria de conversión binario a 7 segmentos se puede utilizar la sentencia WHEN...ELSE:
B(0) <= '1' when ((x = "0000") or (x = "0001") or (x = "0011") or (x = "0100") or (x = "0101") or (x = "0110") or (x = "0111") or (x = "1000") or (x = "1001")) else '0'; B(1) <= '1' when ((x = "0000") or (x = "0010") or (x = "0011") or (x = "0101") or (x = "0110") or (x = "1000") or (x = "1001")) else '0'; B(2) <= '1' when ((x = "0000") or (x = "0010") or (x = "0110") or (x = "1000")) else '0'; B(3) <= '1' when ((x = "0000") or (x = "0010") or (x = "0011") or (x = "0101") or (x = "0110") or (x = "0111") or (x = "1000") or (x = "1001")) else '0'; B(4) <= '1' when ((x = "0000") or (x = "0001") or (x = "0010") or (x = "0011") or (x = "0100") or (x = "0111") or (x = "1000") or (x = "1001")) else '0'; B(5) <= '1' when ((x = "0000") or (x = "0100") or (x = "0101") or (x = "0110") or (x = "1000") or (x = "1001")) else '0'; B(6) <= '1' when ((x = "0010") or (x = "0011") or (x = "0100") or (x = "0101") or (x = "0110") or (x = "1000") or (x = "1001")) else '0';
Como se puede apreciar en este caso, las 7 líneas de código debe "ejecutarse" de forma concurrente. Dicho de otra forma: se describen 7 circuitos combinacionales que deben implementarse en paralelo.
En este caso x es la salida del latch mientras que B es la salida de la FPGA que está conectada al display de 7 segmentos. En este caso se ha usado un display de cátodo común por lo que para encender un segmento del display hay que emitir un ‘1’ en la salida correspondiente.
VHDL de la lógica secuencial
La lógica secuencial se divide en la lógica del registro de desplazamiento que se ha implementado utilizando el clásico modelo RTL:
d_reg <= data_in & q_reg(3 downto 1); --d_reg es q_reg desplazado concatenado con el bit que hay en data_in process(clock_in) --el proceso se activa cuando clock_in cambia begin if (rising_edge(clock_in)) then --cuando hay un flanco de subida q_reg <= d_reg; --se carga d_reg en q_reg end if; end process;
Y la lógica del latch de 4 bits, que se encarga de cargar el registro de desplazamiento (q_reg) en la señal de entrada de la lógica combinatoria para la salida de 7 segmentos (x), y que también se ha implementado utilizando el modelo RTL:
process(latch_in) --el proceso se activa cuando latch_in cambia begin if (rising_edge(latch_in)) then --cuando hay un flanco de subida x <= q_reg; --se carga q_reg en x end if; end process;
En este caso las acciones a realizar no se hacen "siempre" sino que dependen de otras señales (clock_in y latch_in) y debe hacerse una evaluación secuencial (si ocurre esto entonces aquello), por eso se utilizan bloques "process". Nótese que ambos bloques "process" se "ejecutan" en paralelo.
VHDL completo
El código VHDL completo, incluyendo la arquitectura y el port queda como sigue:
library IEEE; use IEEE.STD_LOGIC_1164.ALL; use IEEE.STD_LOGIC_ARITH.ALL; use IEEE.STD_LOGIC_UNSIGNED.ALL; entity SimpleShiftRegister is port ( clock_in : in std_logic; data_in : in std_logic; latch_in : in std_logic; B : out std_logic_vector(6 downto 0) ); end SimpleShiftRegister; architecture behavioral of SimpleShiftRegister is signal d_reg : std_logic_vector(3 downto 0); signal q_reg : std_logic_vector(3 downto 0); signal x : std_logic_vector(3 downto 0); begin d_reg <= data_in & q_reg(3 downto 1); B(0) <= '1' when ((x = "0000") or (x = "0001") or (x = "0011") or (x = "0100") or (x = "0101") or (x = "0110") or (x = "0111") or (x = "1000") or (x = "1001")) else '0'; B(1) <= '1' when ((x = "0000") or (x = "0010") or (x = "0011") or (x = "0101") or (x = "0110") or (x = "1000") or (x = "1001")) else '0'; B(2) <= '1' when ((x = "0000") or (x = "0010") or (x = "0110") or (x = "1000")) else '0'; B(3) <= '1' when ((x = "0000") or (x = "0010") or (x = "0011") or (x = "0101") or (x = "0110") or (x = "0111") or (x = "1000") or (x = "1001")) else '0'; B(4) <= '1' when ((x = "0000") or (x = "0001") or (x = "0010") or (x = "0011") or (x = "0100") or (x = "0111") or (x = "1000") or (x = "1001")) else '0'; B(5) <= '1' when ((x = "0000") or (x = "0100") or (x = "0101") or (x = "0110") or (x = "1000") or (x = "1001")) else '0'; B(6) <= '1' when ((x = "0010") or (x = "0011") or (x = "0100") or (x = "0101") or (x = "0110") or (x = "1000") or (x = "1001")) else '0'; process(clock_in) begin if (rising_edge(clock_in)) then q_reg <= d_reg; end if; end process; process(latch_in) begin if (rising_edge(latch_in)) then x <= q_reg; end if; end process; end behavioral;
Tras compilar y sintetizar este código, la implementación eléctrica generada es la siguiente:
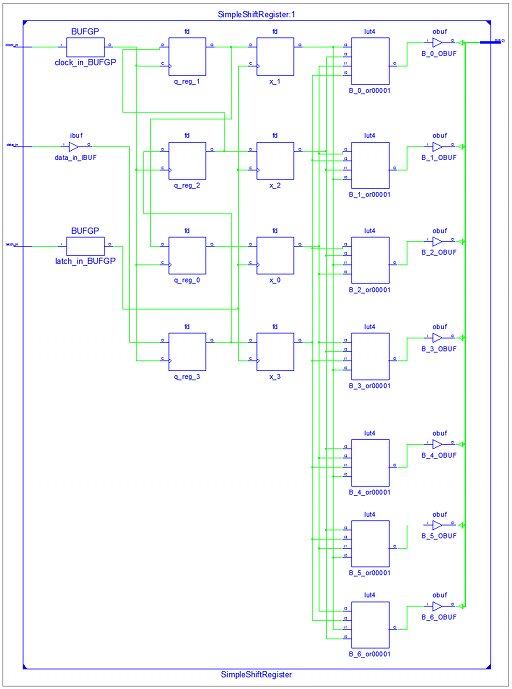
Como se puede ver, tanto el registro de desplazamiento como el latch se implementa mediante biestables D mientras que la lógica combinatoria de conversión de binario a 7 segmentos se implementa mediante LUTs (Look Up Tables), en lugar de mediante puertas lógicas. Esta forma de implementar lógica combinatoria es muy habitual en las FPGAs y los CPLDs.
Conexión con el Arduino
La FPGA funciona a 3.3 voltios mientras que el Arduino funciona a 5 voltios. Es necesario, por tanto adaptar los voltajes. En este caso concreto todas las señales salen del Arduino y entran en la FPGA por lo que se ha optado por hacer una adaptación de voltaje sencilla basada en transistores.
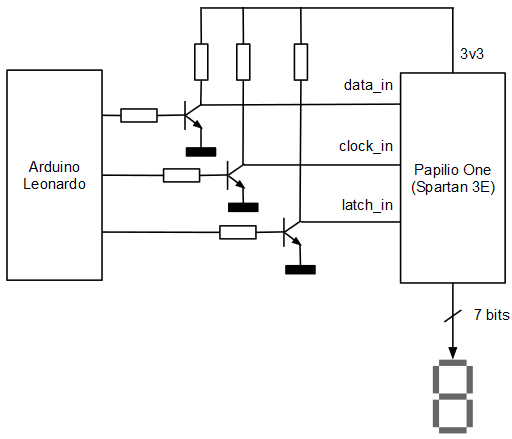
En el Arduino la función encargada de enviar un valor al display de 7 segmentos deberá colocar los datos de forma serie a través del pin data_in usando como reloj clock_in. Se activará latch_in cuando se desee mostrar en el display el valor cargado en el registro de desplazamiento. Obsérvese que al hacer la conversión de voltajes utilizando transistores NPN en configuración de emisor común, la lógica debe ser negada, es decir, para emitir un 1 de 3.3 voltios, emitimos un 0 de 5 voltios y para emitir un 0 de 3.3 voltios, emitimos un 1 de 5 voltios:
const int CLK_PIN = 0; const int DATA_PIN = 1; const int LATCH_PIN = 2; #define ONE LOW #define ZERO HIGH void byteOut(unsigned char v) { for (unsigned char i = 0; i < 4; i++) { if ((v & 1) != 0) digitalWrite(DATA_PIN, ONE); else digitalWrite(DATA_PIN, ZERO); delay(1); digitalWrite(CLK_PIN, ONE); delay(1); digitalWrite(CLK_PIN, ZERO); delay(1); v = v >> 1; } digitalWrite(LATCH_PIN, ONE); delay(1); digitalWrite(LATCH_PIN, ZERO); delay(1); }
A continuación puede verse un vídeo con el invento en funcionamiento:
Algunos enlaces para empezar con VHDL (en español)
Lista de reproducción de YouTube del profesor Carlos Fajardo sobre VHDL - Vídeos muy amenos y fáciles de seguir.
Libro online "Programación en VHDL" - Muy buen libro, aunque le echo en falta más ejemplos y ejercicios.
[ añadir comentario ] ( 2778 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 4901 )
( 3 / 4901 )La utilización de lógica borrosa o difusa (“fuzzy”) para el control de procesos permite abordar este tipo de problemas desde una perspectiva más "humana" ya que las reglas de la lógica borrosa son enunciados fácilmente comprensibles por una persona ajena a la teoría del control y su ajuste es más intuitivo que en el caso de controladores más "puros" como el PID. A lo largo de este post se abordará el control de velocidad de un sencillo motor DC mediante lógica borrosa utilizando sólo un puñado de reglas.
El problema
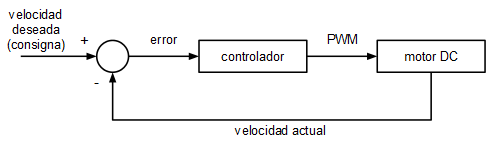
Se parte de un lazo de control estándar, el mismo que se utilizó cuando se implementó el control PID:
La velocidad se lee mediante un sencillo encoder compuesto por un disco pintado mitad de blanco y mitad de negro y por un sensor infrarrojo de tipo reflexivo (el CNY70, de los que suelen usarse en robots siguelineas).
El motor es accionado a través de una de las salidas PWM del microcontrolador mediante un transistor NPN de potencia.
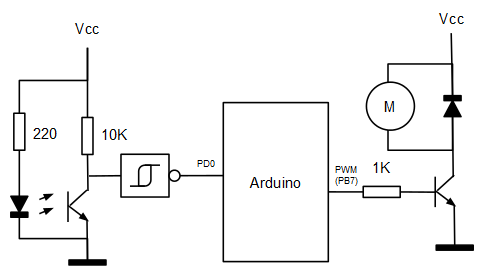
El esquema es exactamente el mismo que el utilizado en el post anterior.
Lectura de la velocidad angular
Para leer la velocidad angular se conecta la salida del sensor infrarrojo reflexivo (en concreto la salida del inversor schmitt) a una entrada de interrupción externa del microcontrolador y se programa dicha interrupción externa para que se dispare en uno de los flancos (subida o bajada, pero no en ambos a la vez). De esta forma y al estar el disco pintado mitad negro y mitad blanco, cada interrupción se corresponderá con una vuelta del eje de rotación.
float RPMReader::rpm; void RPMReader::init() { DDRD &= 0xFE; // PD0 as input cli(); EICRA = (1 << ISC01) | (1 << ISC00); // external INT0 EIMSK = (1 << INT0); sei(); Chronometer::init(); Chronometer::microseconds = 0; } void RPMReader::__isr() { uint32_t delta = Chronometer::microseconds; Chronometer::microseconds = 0; if (delta > 0) rpm = (((float) 1) / delta) * 60000000; EIFR |= (1 << INTF0); } ISR(INT0_vect) { RPMReader::__isr(); }
Cada vez que se ejecuta la interrupción (da una vuelta el eje de rotación) se obtiene la cantidad de microsegundos que han pasado desde la anterior vuelta y se calcula la velocidad angular:
uint32_t delta = Chronometer::microseconds; Chronometer::microseconds = 0; if (delta > 0) rpm = (((float) 1) / delta) * 60000000;
Señal PWM de salida
La salida del controlador borroso no es en este caso directamente el valor absoluto PWM, sino el "incremento" (o una especie de derivada) de dicho valor PWM. Esto simplifica el diseño del controlador borroso pero complica la etapa de salida, ya que hay que poner un "integrador" a la salida del controlador que convierta los incrementos PWM en valores absolutos PWM.

Afortunadamente este "integrador" no es más que un acumulador en el que se van sumando, en cada iteración, los incrementos que emite el controlador borroso. Es esta suma la que se emite como PWM para accionar el motor.
SpeedDeltaFuzzyValueWriter::SpeedDeltaFuzzyValueWriter() { this->sum = 0; } void SpeedDeltaFuzzyValueWriter::setValue(float v) { this->sum += v; if (this->sum > 255) this->sum = 255; else if (this->sum < 0) this->sum = 0; uint8_t aux = (uint8_t) this->sum; PWM::setPB7Value(aux); }
Control borroso
Para realizar el controlador se plantea como variable de entrada al mismo el error de la velocidad de rotación (deseada - actual) en revoluciones por minuto (RPM) y como variable de salida, el incremento (una especie de derivada) del ciclo de trabajo de la señal PWM que alimenta al motor DC. Se definen unos sencillos conjuntos borrosos asociados a cada una de estas dos variables:
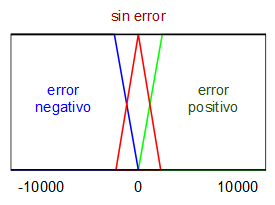
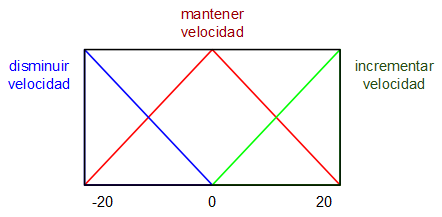
Mientras que las reglas de lógica borrosa que se van a utilizar son las siguientes:
SI (error ES error negativo) ENTONCES salida ES decrementar velocidad
SI (error ES sin error) ENTONCES salida ES mantener velocidad
SI (error ES error positivo) ENTONCES salida ES incrementar velocidad
Como puede apreciarse, las reglas son sencillas y fáciles de ajustar, de recordar y de mantener. Además, el hecho de que la variable de salida sea un incremento en lugar de un valor absoluto simplifica enormemente las reglas y los conjuntos.
Ejemplo 1
Supongamos que queremos alcanzar una velocidad de 3000 RPM y que la velocidad actual medida por el sensor de velocidad es de 2000 RPM, el error será, por tanto de 1000 RPM (consigna - valor real). Lo primero que se hace es “borrosificar” o “fuzzyficar” esta lectura:
Para la expresión “(error ES error negativo)” se calcula el grado de pertenencia de 1000 RPM al conjunto borroso “error negativo”, para la expresión “(error ES sin error)” se calcula el grado de pertenencia de 1000 RPM al conjunto borroso “sin error” y para la expresión “(error ES error positivo)” se calcula el grado de pertenencia de 1000 RPM al conjunto borroso “error positivo”:
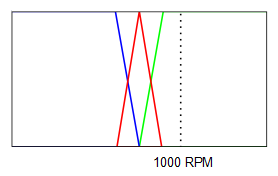
Como se puede ver:
$$\mu_{error \space negativo}(1000)=0$$
$$\mu_{sin \space error}(1000)=0$$
$$\mu_{error \space positivo}(1000)=1$$
Por lo tanto, para la salida:
$$\mu_{decrementar \space velocidad}(\Delta PWM)=0$$
$$\mu_{mantener \space velocidad}(\Delta PWM)=0$$
$$\mu_{incrementar \space velocidad}(\Delta PWM)=1$$
A continuación se calcula mediante el método de la media ponderada de centros, el valor de la salida:
$$\Delta PWM={0·C_{dec. \space velocidad}+0·C_{mant. \space velocidad}+1·C_{inc. \space velocidad} \over 0+0+1}=C_{inc. \space velocidad}=20$$
En este caso el resultado el directamente el centro del conjunto borroso “incrementar velocidad”, que vale 20, con lo que incrementamos la velocidad.
Ejemplo 2
Supongamos ahora que queremos alcanzar la misma velocidad de 3000 RPM y que la velocidad actual medida por el sensor de velocidad es de 3050 RPM, el error será, por tanto de -50 RPM (consigna - valor real). Lo primero que se hace de nuevo es “borrosificar” o “fuzzyficar” esta lectura:
Se calculan los diferentes grados de pertenencia:
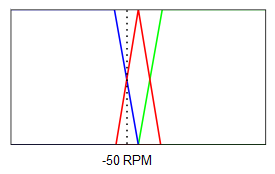
Como se puede ver:
$$\mu_{error \space negativo}(-50)=0.5$$
$$\mu_{sin \space error}(-50)=0.5$$
$$\mu_{error \space positivo}(-50)=0$$
Por lo tanto, para la salida:
$$\mu_{decrementar \space velocidad}(\Delta PWM)=0.5$$
$$\mu_{mantener \space velocidad}(\Delta PWM)=0.5$$
$$\mu_{incrementar \space velocidad}(\Delta PWM)=0$$
A continuación se calcula mediante el método de la media ponderada de centros, el valor de la salida:
$$\Delta PWM={0.5·C_{dec. \space velocidad}+0.5·C_{mant. \space velocidad}+0·C_{inc. \space velocidad} \over 0.5+0.5+0}=-10$$
Un valor de -10 en el incremento del PWM, disminuye dicho valor y, por tanto, hace que se disminuya la velocidad del motor.
En condiciones ideales, con una entrada de error de 0 RPM tendríamos:
$$\mu_{error \space negativo}(0)=0$$
$$\mu_{sin \space error}(0)=1$$
$$\mu_{error \space positivo}(0)=0$$
Por lo tanto, para la salida:
$$\mu_{decrementar \space velocidad}(\Delta PWM)=0$$
$$\mu_{mantener \space velocidad}(\Delta PWM)=1$$
$$\mu_{incrementar \space velocidad}(\Delta PWM)=0$$
Y haciendo la “desborrosificación” o “defuzzyficación” nos sale:
$$\Delta PWM={0·C_{dec. \space velocidad}+1·C_{mant. \space velocidad}+0·C_{inc. \space velocidad} \over 0+1+0}=C_{mant. \space velocidad}=0$$
Un incremento del valor PWM de 0, con lo que no cambiamos la velocidad del motor.
Para dotar al sistema de un comportamiento más estable, en los sistemas reales, suele tomarse también como entrada la derivada de la velocidad angular y establecer reglas que hagan variar el PWM en función de esta otra entrada. En este caso, por simplicidad, se ha optado por utilizar como entrada sólo la velocidad angular.
Implementación
La implementación se ha realizado en C++ y las clases definidas pueden dividirse en dos grupos: las que hacen de interfaz con hardware interno, entrada y salida (lectura del sensor de infrarrojos reflexivo para calcular la velocidad angular, salida PWM, timers, etc.) y las que forman parte del motor de inferencia borroso (expresiones, conjuntos borrosos, variables lingüísticas, reglas, etc.)
Diagrama de clases 1:
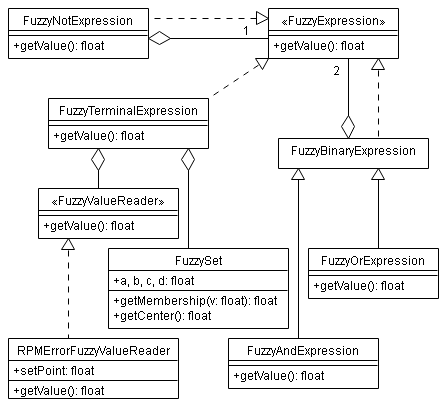
Diagrama de clases 2:
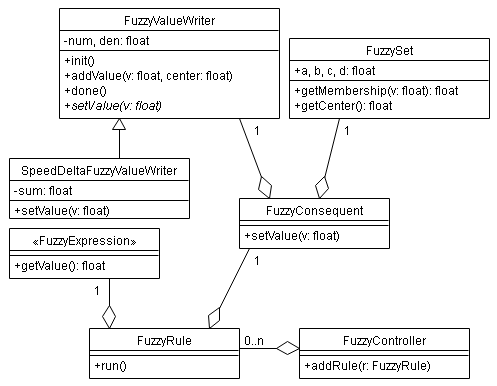
Los conjuntos borrosos (clase FuzzySet) se definen de forma trapezoidal:
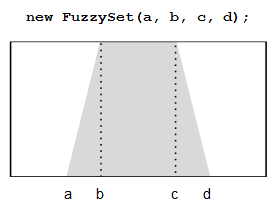
En el caso concreto que nos ocupa los conjuntos estarán, por tanto, definidos así:
FuzzySet negativeError(-10000, -10000, -100, 0); FuzzySet noError(-100, 0, 0, 100); FuzzySet positiveError(0, 100, 10000, 10000); FuzzySet decreaseSpeed(-20, -20, -20, 0); FuzzySet keepSpeed(-20, 0, 0, 20); FuzzySet increaseSpeed(0, 20, 20, 20);
Cada regla de inferencia borrosa estará definida por un antecedente (objeto de clase FuzzyExpression o derivadas) y por un consecuente (objeto de clase FuzzyConsequent).
FuzzyController c;
c.addRule(
new FuzzyTerminalExpression(entrada1, conjunto1),
new FuzzyConsequent(salida1, conjunto3)
); // SI (entrada1 ES conjunto1) ENTONCES salida1 ES conjunto3
En el antecedente podemos hacer combinaciones “Y”, “O” y “NO” utilizando las clases FuzzyAndExpression, FuzzyOrExpression y FuzzyNotExpression respectivamente.
c.addRule(
new FuzzyAndExpression(
new FuzzyTerminalExpression(entrada1, conjunto1),
new FuzzyTerminalExpression(entrada2, conjunto2)
),
new FuzzyConsequent(salida1, conjunto3)
); // SI (entrada1 ES conjunto1) Y (entrada2 ES conjunto2) ENTONCES salida1 ES conjunto3
De esta forma podemos crear reglas de inferencia borrosa tan complejas como queramos. Se ha aprovechado, además, la capacidad que tiene C++ de redefinir operadores y se han usado los operadores “&&”, “||”, “!” y “%” como sinónimos de FuzzyAndExpression, FuzzyOrExpression, FuzzyNotExpression y FuzzyTerminalExpression, respectivamente:
FuzzyExpression &avelino::operator % (FuzzyValueReader &vr, FuzzySet &fs) { FuzzyExpression *ret = FuzzyTerminalExpression::getInstance(vr, fs); return *ret; } FuzzyExpression &avelino::operator && (FuzzyExpression &e1, FuzzyExpression &e2) { FuzzyExpression *ret = FuzzyAndExpression::getInstance(e1, e2); return *ret; } FuzzyExpression &avelino::operator || (FuzzyExpression &e1, FuzzyExpression &e2) { FuzzyExpression *ret = FuzzyOrExpression::getInstance(e1, e2); return *ret; } FuzzyExpression &avelino::operator ! (FuzzyExpression &e) { FuzzyExpression *ret = FuzzyNotExpression::getInstance(e); return *ret; }
Ahora se puede escribir la regla de ejemplo de antes “SI (entrada1 ES conjunto1) Y (entrada2 ES conjunto2) ENTONCES salida 1 ES conjunto3” de la siguiente manera:
c.addRule(
(entrada1 % conjunto1) && (entrada2 % conjunto2),
new FuzzyConsequent(salida1, conjunto3)
);
Como se puede apreciar, la sintaxis se vuelve más clara y las reglas son más fáciles de leer y de mantener. En el caso que nos ocupa las reglas se definen de la siguiente manera:
c.addRule(
rpmError % negativeError,
new FuzzyConsequent(speedDelta, decreaseSpeed)
);
c.addRule(
rpmError % noError,
new FuzzyConsequent(speedDelta, keepSpeed)
);
c.addRule(
rpmError % positiveError,
new FuzzyConsequent(speedDelta, increaseSpeed)
);
Finalmente, en el bucle principal de la aplicación lo único que se hace es iterar el motor de inferencia borroso (FuzzyController::run) cada 200 milisegundos:
DDRC |= 0x80; while (true) { if (Chronometer::microseconds2 > 200000) { // each 200ms Chronometer::microseconds2 = 0; c.run(); } // turn on led when set point reached if ((RPMReader::rpm >= SET_POINT_LOW) && (RPMReader::rpm <= SET_POINT_HIGH)) PORTC |= 0x80; else PORTC &= 0x7F; }

Todo el código fuente puede descargarse de la sección soft.
[ 2 comentarios ] ( 12403 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 5925 )
( 3 / 5925 )
 Calendario
Calendario




