El STM32F103 es un microcontrolador muy asequible que incluye interfaz USB 2.0. La mayoría de desarrollos USB realizados para esta serie de microcontroladores utiliza la librería STM32Cube, desarrollada por el propio fabricante, de libre uso y que abstrae de los entresijos del protocolo al programador. Abordar, sin embargo, el desarrollo de esta funcionalidad desde cero en este o en otros microcontroladores permite profundizar y mejorar en el conocimiento del propio protocolo USB.



Un repaso rápido del protocolo USB

Aunque aquí intentaré desgranar a grandes rasgos el protocolo, recomiendo siempre las dos grandes y mejores fuentes de información sobre el mismo:

USB made simple
USB in a nutshell

Es de lo mejorcito que hay al respecto por la red ya que el documento oficial es un poco infumable. A nivel eléctrico, se trata de un protocolo serie asíncrono que utiliza dos hilos de señal balanceada. El protocolo consiste en una serie de "endpoints" multiplexados en tiempo y enumerados. Hay tres tipos de endpoint:

Control: usado para transferencias de control del dispositivo. Identificación, configuración, etc.

Bulk: usado para transferencias masivas de datos con control de errores (menos ancho de banda).

Interrupt: usado para transferencias pequeñas de datos pero con tiempo mínimo de entrega garantizado.

Isochronous: usado para transferencias masivas de datos sin control de errores (máximo ancho de banda).

Cada endpoint tiene un número asociado y un tipo. El estándar USB reserva el endpoint 0 como un endpoint de control sobre el que el host (ordenador) envía los mensajes de configuración iniciales al dispositivo que acaba de conectarse.

La secuencia ya se describió en un post anterior en el que se abordó el mismo proyecto pero utilizando el microcontrolador ATmega32u4 de AVR pero la volvemos a indicar a continuación:

1. El host detecta que hay un dispositivo conectado (detecta una resistencia pull up en D+ o en D-)

2. El host inicia una secuencia de reset poniendo a nivel bajo las líneas D- y D+ durante al menos 2.5 us.

3. El host envía un paquete de SETUP para pedir el descriptor de dispositivo al dispositivo. Este descriptor indica el tipo de dispositivo, el código de fabricante, código de producto, etc. Esta primera petición se realiza siempre indicando en el campo longitud la longitud máxima y en la respuesta proveniente del dispositivo, el host es capaz de deducir el tamaño máximo de buffer con el que trabaja el dispositivo. Hay que tener en cuenta que en el caso de dospisitivos low-speed los paquetes son siempre de 8 bytes de datos mientras que en dispositivos full-speed los paquetes pueden ser de 8, 16, 32 o 64 bytes.

4. Tras esta primera petición de descripción de dispositivo el host suele iniciar de nuevo una condición de reset y, a continuación vuelve a pedir el descriptor de dispositivo pero con el tamaño ajustado al tamaño indicado por el dispositivo en la primera petición.

5. Cada dispositivo tiene asignada una dirección en el bus que, tras es reset, es siempre 0. En este instante lo habitual es que el host envíe un paquete de SETUP de tipo SET_ADDRESS para indicarle al dispositivo que a partir de ahora el host se va a comunicar con el dispositivo usando una dirección concreta diferente a 0 y que el dispositivo debe recordar para posteriores paquetes que se transmitan.

6. Ya con la nueva dirección de bus configurada, el host envía otro paquete de SETUP para solicitar el descriptor de configuración. Este descriptor es más grande que el anterior e incluye información sobre la clase de dipositivo y los endpoints que utiliza. El descriptor de dispositivo indica en un campo cuántas configuraciones posee el dispositivo, que suele ser siempre 1, por lo que el host normalmente sólo pide un descriptor de configuración.

7. El host (normalmente el driver instalado en el host) decide qué configuración quiere activar (que suele ser la única) en el dispositivo enviando un paquete de SETUP de tipo SET_CONFIGURATION. A partir de este instante el dispositivo queda conectado y con sus endpoints preparados para recibir y enviar datos propios de la funcionalidad del dispositivo.

La secuencia puede variar ligeramente en función del sistema operativo del host. Hay que recordar que en el protocolo USB el host es siempre el que envía "tokens" al dispositivo, incluso para traer datos desde el dispositivo. Cuando el host quiere enviar datos a un dispositivo hace transferencias de tipo SETUP y OUT mientras que cuando quiere recibir datos del dispositivo, el host hace transferencias de tipo IN pero siempre es el host el que pregunta. Un dispositivo no puede enviar datos a un host hasta que el host mande un token de tipo IN al dispositivo.

Implementación en el STM32F103

La serie STM32F103 es la serie más sencilla y baratita de toda la familia STM32 con soporte USB 2.0 full-speed (en el momento que escribo esto se puede conseguir una placa mínima de desarrollo con STM32F103 por menos de 3 ¤ en AliExpress). La documentación de referencia para programar el módulo USB es algo oscura y no está pensada para que te sumerjas mucho en ella, sino para que utilices la librería STM32Cube que, aunque es open source y permite un uso sin restricciones, su uso le quita toda la gracia al concepto de programar un microcontrolador desde cero :-).

A continuación puede verse la implementación de un dispositivo USB consistente en dos endpoints sencillos de tipo bulk (uno de entrada y otro de salida). La razón para implementar un dispositivo así es el hecho de que desde Linux el driver "usbserial" permite intercambiar datos con cualquier dispositivo USB que cumpla que tenga un endpoint bulk de salida y otro de entrada sin importar su clase, ni el código de fabricante ni de producto. Es un driver ideal para depurar dispositivos USB y que instancia un "/dev/ttyUSB0". Escribiendo en "/dev/ttyUSB0" se envían bytes a través del endpoint de salida mediante paquetes OUT mientras que leyendo de "/dev/ttyUSB0" se reciben bytes desde el dispositivo a través del endpoint de entrada mediante paquetes IN que envía el host.

La función usbDeviceInit se encarga de inicializar los tranceptores y de activar la interrupción de "USB Reset":


A continuación definimos los diferentes descriptores del dispositivo (descriptor de dispositivo, descriptor de configuración y descriptor de cadena 0 que indica los idiomas disponibles en el dispositivo):


Los buffers de recepción y transmisión USB en el caso de STM32 deben ser direccionados y accedidos de forma particular. Desde el punto de vista del subsistema USB, la anchura del bus de datos es de 16 bits, en lugar de 32 bits aunque los datos están alineados a 32 bits. Gráficamente se ve mejor:

Offset desde el punto de     Offset desde el punto de
vista del controlador USB    vista del programa (CPU)
0                            0
1                            1
2                            4
3                            5
4                            8
5                            9
6                            12

Como se puede ver, por cada palabra de 32 bits direccionada desde la CPU sólo se puede acceder a los 16 bits menos significativos. Para leer los 2 primeros bytes de la memoria USB desde la CPU hay que acceder a los 4 primeros bytes de dicha memoria (como si fuese un entero de 32 bits) y quedarnos con los 16 bits menos significativos. Los siguientes 2 bytes no están en los 16 bits más significativos de la primera palabra de 32 bits, sino en los 16 bits menos significativos de la siguiente palabra de 32 bits y así sucesivamente. Teniendo en cuenta esta particularidad se implementan dos funciones de acceso a esta memoria USB para copiar hacia y desde ella:


A continuación definimos las rutinas de interrupción correspondientes. Primero escribimos la rutina usbDeviceISRReset, que se ejecuta en caso de que se genere una interrupción de "USB Reset" provocada por una condición de reset en el bus USB. Dicha condición de reset es iniciada por el host en cuanto detecta un nuevo dispositivo conectado a una de sus bocas USB (es el paso 2 de la secuencia descrita anteriormente):


A continuación se define la rutina principal que atiende las interrupciones USB, usbDeviceISR. Esta función llama, en caso de darse una condición de reset a la función usbDeviceISRReset definida arriba:


Lo primero que hace la rutina es identificar el endpoint por el que se ha producido la transacción. En caso de que la transacción se haya producido a través del endpoint 0 se comprueba si es un token SETUP u OUT y, si es un token SETUP, se parsea y se mira a ver si el host está mandando algo (configuraciones) o si lo está pidiendo (descriptores). Si el host está pidiendo algo, hay que rellenar el buffer de transmisión con los datos que necesita, pues la siguiente transacción que realizará el host a través del endpoint 0 será utilizando uno o varios tokens IN y para entonces los datos tienen que estar ya preparados en dicho búffer.

Recordemos algunos elementos básicos sobre cómo son las transferencias USB a través del endpoint 0:

Control: Es un endpoint que debe ser siempre configurado como de tipo "Control" y es bidireccional. Un dispositivo puede definir endpoints de control adicionales pero el endpoint 0 de control siempre debe estar disponible.

Transacciones SETUP: Los endpoints configurados como de control permiten transferir un tipo especial de token denominado SETUP. Este token puede ser de entrada o de salida (siempre desde el punto de vista del host).

Transacciones SETUP de salida: El host manda un token SETUP, a continuación envía cero o más tokens OUT con datos anexos y por último manda un token IN para que el dispositivo mande 0 bytes a modo de ACK.

Transacciones SETUP de entrada: El host manda un token SETUP, a continuación envía cero o más tokens IN para recibir datos del dispositivo y al final el host manda un token OUT con 0 bytes anexos a modo de ACK hacia el dispositivo.

Si la transacción se ha producido en el endpoint 1 o 2, se asume que es una transacción simple de tipo bulk:

Endpoint 1: Es un endpoint configurado como de tipo IN y en esta implementación no hace nada, pues el STM32 no manda ningún dato cuando es leido a través del USB.
Endpoint 2: Es un endpoint configurado como de tipo OUT. Por lo tanto, el STM32 recibe por aquí los datos que son enviados desde el host y los manda formateados a través de la USART.

Nos limitamos a mandar por la USART1 todo lo que entra a través del endpoint de tipo "bulk out", mientras que las lecturas desde el host al endpoint de tipo "bulk in" devuelven siempre 0 bytes.

Para cargar el módulo "usbserial" en el kernel simplemente hay que hacer:

modprobe usbserial vendor=0xf055 product=0x0001

Esto nos permite comunicarnos con el dispositivo desde la misma shell:

echo "Hola, caracola" > /dev/ttyUSB1

Partiendo de este código se pueden implementar multitud de dispositivos USB en este microcontrolador (Mass storage, HID, DFU, etc.). Todo el código fuente puede descargarse desde la sección soft.

Quiero agradecer a Jian Jiao (mculabs.net) la ayuda prestada a la hora de comprender algunos entresijos en la programación del módulo USB del microcontrolador STM32.

[ añadir comentario ] ( 2456 visualizaciones )   |  [ 0 trackbacks ]   |  enlace permanente  |   ( 3 / 4686 )

---

El efecto "shuffle" o "swing" es un efecto muy utilizado en producción musical para humanizar y meter mas "groove" a canciones reproducidas por un secuenciador. El efecto consiste básicamente en adelantar o atrasar el disparo de determinadas notas durante algunos milisegundos para dar sensación de "humanidad" a la cadencia de la música. A lo largo de este post se abordará la implementación en C++ sobre Arduino de un "shuffler" MIDI para secuencias 4/4.

La forma más estándar de "shuffle" en secuencias musicales de 4/4 es la que consiste en retrasar una cantidad de tiempo determinada (milisegundos) la segunda y la cuarta semicorchea después de cada negra:

*----.----.----.----*----.----.----.----*----.----.----.----*----.----.----.---- Compás 4/4 estándar
*------.--.------.--*------.--.------.--*------.--.------.--*------.--.------.-- Compás de 4/4 con "shuffle"

Los asteriscos determinan las negras (4 negras por cada compás de 4/4) y los puntos determinan las semicorcheas (4 semicorcheas por cada negra). El concepto es muy sencillo, aunque a la hora de implementarlo en MIDI hay que tener en cuenta algunos aspectos importantes.

Protocolo MIDI

El protocolo MIDI es un protocolo muy sencillo por el que se envían eventos e información musical. No es objetivo de este post el explicar el protocolo ni los mensajes MIDI (cualquier búsqueda sobre "midi protocol" en la red nos dará acceso a centenares de páginas donde lo explican muy bien) aunque sí nos centraremos en los mensajes que más nos interesan de cara a implementar nuestro shuffler.

Dentro de los mensajes MIDI hay unos especiales denominados de tiempo real que son transmitidos por los secuenciadores cuando están reproduciendo una secuencia MIDI pregrabada:

0xF8: "timing clock" se envía 24 veces por cada negra.
0xFA: "start" indica que se va a iniciar la reproducción de una secuencia. Este mensaje es seguido de forma inmediata por el primer 0xF8.
0xFB: "continue" indica que se reanuda la secuencia por donde se paró.
0xFC: "stop" indica que se para la secuencia.

Por tanto, si en nuestro secuenciador musical tenemos una canción con un tempo de 120 negras por minuto, al emitir dicha secuencia por un cable MIDI, de forma intercalada con los mensaje de activación y desactivación de las notas y demás, irán entremezclados mensajes 0xF8 a razón de 24 por cada negra, es decir:

$${{120 \times 24} \over 60} = 48\;mensajes/segundo$$

Nótese que la cantidad de mensajes 0xF8 enviados por unidad de tiempo no depende de la velocidad de transmisión MIDI, sino del tempo de la secuencia musical que se esté reproduciendo. Si cada vez que nos llegue un mensaje 0xF8 desde el secuenciador vamos contando de 0 a 23 dando la vuelta de nuevo a 0 cada vez que llegamos a 24 tenemos que los mensaje 0xF8 coinciden en el tiempo con las negras y semicorcheas de la forma que indica la siguiente tabla:

n                 s                 s                 s
0  1  2  3  4  5  6  7  8  9  10 11 12 13 14 15 16 17 18 19 20 21 22 23

En esta tabla se puede ver que la negra (el beat) coincide con el contador de mensajes 0xF8 recibidos a 0 mientras que las tres semicorcheas siguientes coinciden con ese mismo contador a 6, a 12 y a 18. Ahora tenemos una base de tiempo sólida que podemos aprovechar para implementar nuestro efecto shuffle: Lo que hay que hacer es atrasar en el tiempo los mensajes de "note on" y "note off" que lleguen entre el instante 6 y el 12 y entre el instante 18 y 0 de la siguiente negra.

n                 s                 s                 s
0  1  2  3  4  5  6  7  8  9  10 11 12 13 14 15 16 17 18 19 20 21 22 23
                  +--------> atrasar                  +--------> atrasar

Dicho atraso no puede ser tal que nuestro shuffler emita notas fuera de orden por lo que el retraso en el tiempo debe ser proporcional (una nota que llegue entre los instantes 6 y el 7 será atrasada más que una que llegue entre los instantes 9 y 10 pero la primera nunca debe emitirse depués de la segunda, debemos garantizar el orden de llegada de los eventos "note on" y "note off").

Algoritmo propuesto

El MIDI shuffler se plantea como un filtro MIDI, un dispositivo con una entrada MIDI y una salida MIDI que se intercala entre el secuenciador y los sintetizadores. La salida MIDI del secuenciador irá conectada a la entrada MIDI del shuffler y la salida MIDI del shuffler irá conectada a la entrada MIDI de los secuenciadores. A continuación se plantea una propuesta de pseudocódigo para el MIDI shuffler:

iniciarShuffler
    estado := ESPERAR_START_MIDI
fin iniciarShuffler
 
getInstanteAtrasado(t)
    ret := (tamSemicorchea - tamReducido) + ((t + tamReducido) / tamSemicorchea)
    devolver ret
fin getInstanteAtrasado
 
byteMIDIRecibido(byte)
    enviar := SÍ
    si (estado = ESPERAR_START_MIDI) entonces
        si (byte = 0xFA) entonces
            colaRetraso.borrar()
            estado := ESPERAR_PRIMER_CLOCK_MIDI
        fin sin
    en otro caso, si (estado = ESPERAR_PRIMER_CLOCK_MIDI) entonces
        si (byte = 0xF8) entonces
            estado := ESPERAR_CLOCK_MIDI
            contadorReloj := 6
            indiceSemicorchea := 0
            timer.iniciar()
        fin si
    en otro caso, si (estado = ESPERAR_CLOCK_MIDI) entonces
        si (byte = 0xF8) entonces
            contadorReloj := contadorReloj - 1
            si (contadorReloj = 0) entonces
                si ((indiceSemicorchea = 0) ó (indiceSemicorchea = 2)) entonces
                    tamSemicorchea = timer.getValor()
                    tamReducido = (temSemicorchea * (100 - PERCENT)) / 100
                fin si
                contadorReloj := 6
                indiceSemicorchea := (indiceSemicorchea + 1) mod 4
                timer.parar()
                timer.iniciar()
            fin si
        en otro caso, si (esEventoNota(byte) y ((indiceSemicorchea = 1) ó (indiceSemicorchea = 3)) entonces
            t := getInstanteAtrasado(timer.getValor())
            colaRetraso.meter({byte, t})
            enviar := NO
        en otro caso, si (byte = 0xFC)
            estado := ESPERAR_START_MIDI
        fin si
    fin si
    si (enviar = SÍ) entonces
        enviar(byte)
    fin si
fin byteMIDIRecibido
 
principal
    siempre hacer
        si ((indiceSemicorchea = 1) ó (indiceSemicorchea = 3)) entonces
            t := timer.getValor()
            mientras (colaRetraso.hayAlgo()) hacer
                d := colaRetraso.getCabeza()
                si (d.t <= t) entonces
                    colaRetraso.sacar()
                    enviar(d.byte)
                en otro caso
                    salir del bucle
                fin si
            fin mientras
        fin si
    fin siempre
fin principal

Lo que hace el algoritmo es aprovechar el intervalo entre el midi clock 0 y el 5 para calcular el tiempo en unidades de timer que dura una semicorchea. El objeto "timer" es un timer de bastante resolución que se arranca en el instante 0 y se para en el instante 6. En ese instante 6, una vez parado el timer, se anota la cuenta del mismo como tamSemicorchea (para indicar que es el tamaño en ticks de nuestro contador de lo que dura una semicorchea) y se calcula tamReducido a partir del porcentaje de "shuffle" que queramos (un shuffle del 0% da un tamReducido = tamSemicorchea, mientras que un shuffle del 100% da un tamReducido = 0).

instante  semicorchea   acción
0         0             Iniciar timer de alta resolución
1
2
3
4
5
6         1             Anotar cuenta del timer, pararlo
7                       y volver a iniciarlo. Encolar cualquier
8                       evento "note on" o "note off" que llegue
9                       en este intervalo calculando su instante
10                      de emisión con una regla de tres.
11
12        2             La misma que la semicorchea 0
13
14
15
16
17
18        3             La misma que la semicorchea 1
19
20
21
22
23

Entre los instantes 6 y el 11 lo que se hace es encolar los eventos de "note on" y "note off" que vayan llegando calculándoles en el momento que llegan, en qué instante del tick del timer deben ser transmitidos haciendo una regla de tres (en getInstanteAtrasado) y metiendo cada una de estas parejas de valores (byte e instante que debe ser transmitido) en la cola "colaRetraso".

Lo mismo se hace para los instantes de tiempo 12 al 17 y 18 al 23, respectivamente.

Ya tenemos los eventos atrasados metidos en una cola (para garantizar que el orden de emisión sea el mismo que el de recepción), ahora lo que hay que hacer es emitirlos en el instante que corresponda. y de esto se encarga el procedimiento principal en su bucle infinito. Este procedimiento principal ejecuta un bucle infinito que lo que hace es inspeccionar si hay algo que enviar en la cola "colaRetraso", si hay algo que debe ser enviado (su instante de envío es menor o igual al valor actual del timer) lo envía y lo quita de la cola. El procedimiente byteMIDIRecibido es invocado cada vez que llega un byte por el puerto MIDI.

El circuito

El MIDI shuffler, como se comentó antes, hace de filtro MIDI con una entrada y una salida. La cantidad de efecto shuffle se controla mediante un potenciómetro conectado a una de las entradas analógicas del Arduino.

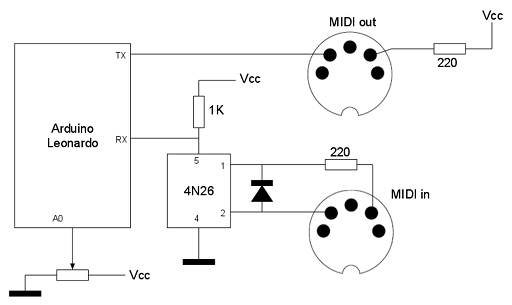
Con el potenciómetro al mínimo se aplica un efecto shuffle del 0% (sin efecto shuffle) mientras que con el potenciómetro al máximo se aplica un efecto shuffle del 50% (valores superiores al 50% genera unos resultados muy extremos).

Implementación en C++

A pesar de que en el algoritmo propuesto el procedimiento byteMIDIRecibido se supone que es invocado de forma asíncrona por el sistema cada vez que llega un byte por el puerto MIDI, lo cierto es que es más sencillo si en la rutina de interrupción de la UART encolamos los bytes MIDI que van llegando por la entrada MIDI y luego los vamos sirviendo en el bucle principal antes de comprobar el estado de la colaRetraso, haciéndolo de esta forma evitamos colisiones y la necesidad de hacer que colaRetraso sea reentrante.


A continuación puede verse un vídeo con el MIDI shuffler en acción (obviamente, hay que poner el audio para que se oiga :-) )



Todo el código fuente puede descargarse de la sección soft.

[ añadir comentario ] ( 2214 visualizaciones )   |  [ 0 trackbacks ]   |  enlace permanente  |   ( 3 / 14047 )

---

Las redes neuronales son un tópico que se ha vuelto a poner de moda gracias al concepto del "deep learning" y a la irrupción de las redes neuronales convolucionales, que han revolucionado, sobre todo, las técnicas de reconocimiento de imágenes. No vamos a llegar tan lejos: implementaremos un sencillo perceptrón multicapa (MLP) en un Arduino que permita a este aprender y predecir el comportamiento de un usuario que acciona unos botones. No es un juego especialmente entretenido pero sirve como prueba de concepto de la implementación de redes neuronales artificiales sobre sistemas embebidos.

Perceptrón multicapa (MLP)

En un post anterior se explicaron los fundamentos teóricos de los perceptrones multicapa. Tenemos un conjunto de neuronas dispuestas en cascada, las de un extremo son las neuronas de entrada y las del otro extremo son las neuronas de salida.



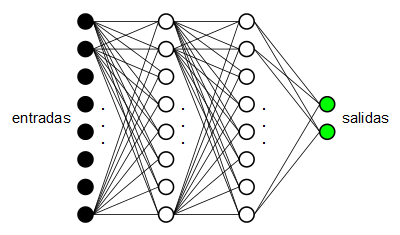
Cada capa de neuronas está conectada con la capa inmediatamente anterior mediante un conjunto de pesos sinápticos que determinan el nivel de influencia de cada neurona de la capa (i-1)-ésima con cada neurona de la capa i-ésima. Los valores de entrada pasan por la matriz de pesos sinápticos que une la capa de entrada con la primera capa intermedia y determinan los valores de las neuronas de la primera capa oculta, a continuación este primera capa oculta propaga sus valores a través de otra matriz de pesos que une dicha capa con la siguiente y así sucesivamente hasta llegar a la capa de salida. La salida del perceptrón multicapa serán las salidas de las neuronas de la última capa.

La salida de cada neurona oculta y de salida viene determinada por:
$$suma^{o}_{pk} = \sum_{j=1}^{L}w_{kj}^{o}y_{pj} + \theta_{k}^{o}$$
$$y_{pk}=f_{k}^{o}(suma^{o}_{pk})$$
Siendo:
$w_{kj}^{o}$ el peso sináptico de la neurona $j$ de la capa anterior sobre la neurona $k$ de la capa actual.
$f$ la función de activación (en este caso la sigmoide).
$$f(x) = {{1} \over {1+e^{-x}}}$$
Cada neurona puede representarse de forma gráfica de la siguiente manera:

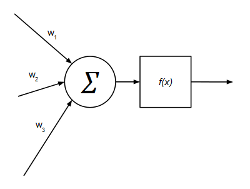
Por ejemplo, un perceptrón multicapa con 6 entradas, 2 salidas y una capa ocultas con 4 neuronas tendrá la siguiente configuración:

A0 = {a01, a02, a03, a04, a05, a06}   <-- capa de entrada
W0,1 = {                              <-- pesos sinápticos entre la entrada y la capa oculta
    w11 w12 w13 w14 w15 w16
    w21 w22 w23 w24 w25 w26
    w31 w32 w33 w34 w35 w36
    w41 w42 w43 w44 w45 w46
}
A1 = {a11 a12 a13 a14}                <-- capa oculta
X1,2 = {                              <-- pesos sinápticos entre la capa oculta y la salida
    x11 x12 x13 x14
    x21 x22 x23 x24
}
A2 = {a21 a22}                        <-- capa de salida

Recomiendo leer el post anterior donde se explica de forma más pormenorizada tanto el perceptrón multicapa como el algoritmo de aprendizaje "backpropagation", el más utilizado y el usado en esta prueba de concepto.

Juego de predicción

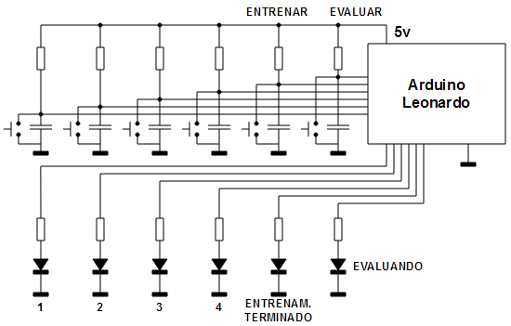
Se plantea un sencillo juego de predicción en el que el Arduino deberá aprenderse los movimientos del usuario que interactúa con él. Se disponen 4 pulsadores y 4 leds (a cada led le corresponde un botón y viceversa). Se incluyen además dos pulsadores adicionales etiquetados como "ENTRENAR" y "EVALUAR" y dos leds adicionales etiquetados como "ENTRENAMIENTO TERMINADO" y "EVALUANDO". Se implementa una red neuronal de tipo MLP con 8 entradas, una capa oculta de 8 neuronas y una capa de salida de 4 neuronas. 4 de las neuronas de entrada recogen las entradas de los 4 pulsadores (1 = pulsado, 0 = no pulsado) y las 4 neuronas de entrada restantes reciben el valor de los pulsadores del instante anterior (es una forma de dar memoria a la red), las cuatro neuronas de salida están conectadas a los 4 leds de salida (encendido = salida de la neurona mayor que 0.5, apagado = en caso contrario).

En modo evaluación el Arduino cada vez que detecta la pulsación de un botón aplica los valores correspondientes a las 8 neuronas de entrada, evalúa el MLP y emite el valor de las 4 neuronas de salida a los leds. En modo entrenamiento la red se va entrenando a sí misma observando las pulsaciones del usuario. La mecánica del "juego" es la siguiente:

1. Nada más arrancar el Arduino, inicia en modo EVALUACIÓN e ilumina el led "EVALUANDO". En este modo cada vez que se pulsa uno de los 4 pulsadores de entrada se evalúa la red neuronal y se emite la salida correspondiente. Como inicialmente los pesos sinápticos son aleatorios, los leds actuarán de forma aleatoria en función de la entrada.

2. Cuando queramos entrenar la red neuronal, pulsamos "ENTRENAR". Esto hace que el led "EVALUANDO" se apague para indicar que estamos en modo aprendizaje y la red entra en modo de aprendizaje. El usuario empieza a accionar los pulsadores en el orden que quiera, se asume una secuencia de cuatro pulsaciones de tal manera que cada cuatro pulsaciones, la red es entrenada para que sea capaz de aprenderse la secuencia. Cada vez que terminamos de introducir una secuencia (cuatro pulsaciones), la red es entrenada con la secuencia introducida y se ilumina el led "ENTRENAMIENTO TERMINADO", si seguimos repitiendo la secuencia afianzaremos el aprendizaje de la red neuronal.

3. Una vez que el led "ENTRENAMIENTO TERMINADO" se haya iluminado al menos una vez podemos volver al modo de evaluación accionando el pulsador "EVALUAR". Al entrar de nuevo en el modo de evaluación se iluminará el led "EVALUANDO". Tras el entrenamiento la red tendrá los pesos sinápticos modificados por el aprendizaje de tal manera que intentará predecir qué pulsador accionará el jugador en cada momento.

Veamos un ejemplo:

1. Encendemos y esperamos a que se encienda el led "EVALUANDO". Comprobamos que al accionar cualquiera de los 4 pulsadores los leds de salida se encienden y se apagan sin criterio, de forma aleatoria debido a los pesos sinápticos aleatorios.

2. Pulsamos "ENTRENAR" y esperamos a que se apague el led "EVALUANDO". Ahora estamos en modo aprendizaje (o entrenamiento).

3. Nos inventamos una secuencia, por ejemplo {1, 4, 2, 3} y vamos accionando los pulsadores de entrada en ese orden. Cuando pulsemos el último número de la secuencia, el 3, se aplicará el algoritmo de aprendizaje para entrenar la red neuronal y una vez termine, se encenderá el led "ENTRENAMIENTO TERMINADO".

4. Llegamos a este punto podemos seguir entrenando la red con la misma secuencia (volvemos a introducir la secuencia en orden {1, 4, 2, 3}, al pulsar el 1 se apagará el led "ENTRENAMIENTO TERMINADO" y volverá a encenderse cuando pulsemos el 3 para indicar que se ha realizado otro entrenamiento) o podemos pasar al modo de evaluación.

5. Para pasar al modo de evaluación pulsamos "EVALUAR". Esto hará que el led "EVALUANDO" se encienda y ahora podremos probar la red entrenada.

6. En modo evaluación lo que hace la red es tratar de adivinar qué pulsador se accionará en el siguiente movimiento. Por ejemplo en nuestro caso, para la secuencia {1, 4, 2, 3}, ocurrirá lo siguiente:

pulsamos 1 --> se enciende el 4
pulsamos 4 --> se enciende el 2
pulsamos 2 --> se enciende el 3
pulsamos 3 --> se enciende el 1

Como se puede comprobar, la red neuronal se ha aprendido nuestros movimientos correctamente.

Implementación

A continuación puede verse el diagrama de clases utilizado en la implementación del juego de predicción en C++:


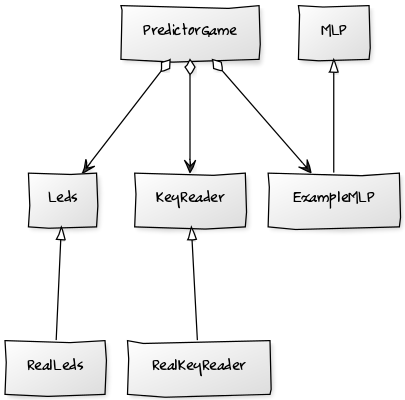
Se trata de una estructura de código muy sencilla. La clase PredictorGame mantiene la máquina de estados principal del juego, lee los pulsadores, controla las luces e incluye también la red neuronal (ExampleMLP). La clase MLP es una clase abstracta que permite definir mediante la implementación de varios de sus métodos virtuales puros la topología de un perceptrón multicapa cualquiera (entradas, capas ocultas y neuronas de salida). La clase ExampleMLP es una especialización de MLP con la topología descrita: 8 entradas, 1 capa intermedia oculta con 8 neuronas y una capa de salida de 4 neuronas.


El código fuente está organizado de tal manera que el que es independiente de la plataforma (clases MultilayerPerceptron, ExampleMultilayerPerceptron, KeyReader, Leds y PredictorGame) se encuentra en la carpeta raiz. El código dependiente de cada plataforma se encuentra en la carpeta correspondiente a dicha plataforma: dentro de la carpeta "linux" están las clases "LinuxKeyReader" y "LinuxLeds" así como el fichero "main.cc" para Linux y dentro de la carpeta "arduino" están las clases "RealKeyReader" y "RealLeds" así como el fichero "main.cc" para Arduino. En este caso concreto, las clases "RealKeyReader" y "RealLeds" están especializadas para el patillaje del Arduino Leonardo pero son fácilmente adaptables a otros modelos de Arduino.

Para compilar la versión "linux" basta con entrar en la carpeta "linux" y hacer "make" mientras que para compilar la versión "arduino" hay que ir a la carpeta "arduino", editar el fichero "Makefile", poner los valores adecuados para la carpeta donde está instalado el IDE de Arduino ("ARDUINO_FOLDER") y el puerto serie donde se conecta el Arduino ("SERIAL") y a continuación hacer "make" para generar el fichero "main.hex" y "make install" para tostarlo en el Arduino.

A nivel eléctrico se trata de un circuito sumamente sencillo: 6 pulsadores, con su pequeña red antirrebote cada uno, y 6 leds.

Todo el código está disponible en la sección soft.



[ añadir comentario ] ( 2044 visualizaciones )   |  [ 0 trackbacks ]   |  enlace permanente  |   ( 3 / 5319 )

---

Incluir una entrada analógica en una FPGA pasa, normalmente, por agregar al menos un integrado que haga de ADC. Sin embargo, existen alternativas al ADC tradicional que, aprovechando las características de una FPGA, nos permiten implementar un conversor analógico-digital utilizando muy pocos componentes externos.

Registro de aproximaciones sucesivas (SAR)

Esta técnica utiliza un comparador, una resistencia y un condensador como únicos componentes externos y consume dos pines E/S de la FPGA. Se consigue una resolución en bits arbitraria que sólo dependerá de los valores de R, de C y de la frecuencia de reloj de la FPGA.



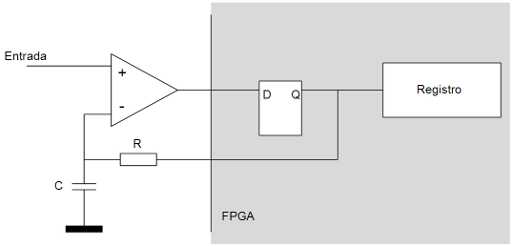
El principio de funcionamiento es muy sencillo: inicialmente el condensador se encuentra descargado y la salida de realimentación (el pin conectado a R) se pone a 1. Esto hace que el condensador empiece a cargarse. En el instante en que el voltaje en el condensador llegue hasta la mitad de Vcc (1.65v en el caso de una FPGA alimentada a 3.3v), la FPGA lee el valor de la entrada digital (el otro pin). Esta entrada está conectada a la salida de un comparador que emitirá 3.3v si el voltaje en la entrada V+ es superior al voltaje en la entrada V- y 0v en caso contrario.

Si la FPGA lee un 0 en esa entrada significará que el voltaje que estamos midiendo en la entrada V+ se encuentra por debajo de Vcc/2 por lo que ya podemos determinar que el bit más significativo del valor convertido es un 0. Si la FGPA lee un 1 en esa entrada significará que el voltaje que estamos midiendo en la entrada V+ se encuentra por encima de Vcc/2 por lo que ya podemos determinar que el bit más significativo del valor convertido es en este caso un 1.



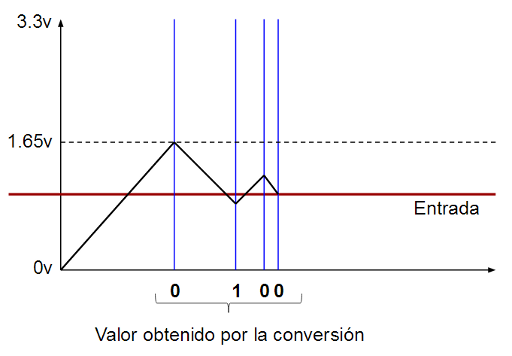
Si la FPGA ha leido un 0 en la entrada de comparación (V+ está por debajo del voltaje que hay en ese instante en los extremos del condensador, Vcc/2), significará que para determinar el siguiente bit hay que bajar el voltaje de la entrada V- (descargar el condensador), por lo que se emite un 0 por el pin conectado a R. Esto provoca que el condensador empiece a descargarse.

Si la FPGA leyó un 1 en la primera comparación (V+ está por encima del voltaje que hay en ese instante en los extremos del condensador, Vcc/2), significará que para determinar el siguiente bit hay que seguir cargando el condensador (la FPGA debe seguir emitiendo un 1 por la pata que conecta a R).

Independientemente de si la FPGA emite un 0 (para descargar el condensador) o un 1 (para seguir cargándolo), espera la mitad de tiempo que la primera vez antes de volver a leer la entrada conectada al comparador. En esta segunda lectura vuelve a hacer lo mismo: Si vale 0 significa que el voltaje del condensador está por encima del voltaje que estamos midiendo (V+) mientras que si vale 1 significa que el voltaje del condensador está por debajo del voltaje que estamos midiendo. En el primer caso el siguiente bit valdrá 0 y se emite un 0 por el pin conectado a R para descargar del condensador. En el segundo caso el siguiente bit valdra 1 y se emitirá un 1 por el pin conectado a R para cargar el condensador. Como puede observar el bit que se emite como valor es el mismo que el que alimenta a la salida conectada a R.

En cada iteración del proceso se espera la mitad de tiempo que la iteración anterior, se empieza siempre por el bit más significativo y se pueden realizar tantas iteraciones como se deseen: La cantidad de bits de resolución de la conversión vendrá determinada por la cantidad de comparaciones que hagamos.

Implementación: el circuito

En este caso se ha implementado una pequeña prueba de concepto: un conversor de 4 bits de resolución usando un amplificador operacional barato LM358N (por AliExpress se pueden adquirir 10 unidades por menos de 2¤ en el momento que escribo estas líneas) para usarlo como comparador, un condensador de 1uF y una resistencia de 10K.

Como FPGA he utilizado una Cyclone II de Altera que pillé hace poco. No es tan potente como la Spartan-3E de Xilinx que he usado en otros montajes pero es compacta, barata y más que suficiente para el ADC.

Implementación: el software

Como se vió en la descripción varios párrafos más arriba, la FPGA debe leer la entrada de comparación en unos instantes determinados: inicialmente debe esperar hasta que el condensador llegue a Vcc/2 para realizar la primera medida, la segunda medida la realizará en la mitad de tiempo que la primera, la tercera en la mitad de tiempo que la segunda y así sucesivamente.

En nuestro caso, asumiendo un condensador de 1uF (C = 0.000001), una resistencia de 10K (R = 10000), la salida de la FPGA que está conectada a R, a la que etiquetaremos como Vi con un valor de 3.3v y la entrada inversora del comparador, a la que llamaremos Vo con un valor de 1.65v (3.3 / 2), tenemos que:

$$t=-R \times C \times log\left({{V_o - V_i} \over {V_o(0) - V_i}}\right)$$
$$t = -10000 \times 0.000001 \times log\left({{1.65 - 3.3} \over {0 - 3.3}}\right) = 0.006931471805599453 \; s$$

Es el tiempo que tarda Vo en valer 1.65v (la mitad de Vcc = 3.3v) partiendo de 0v (condensador totalmente descargado). Esta ecuación es la solución analítica a la ecuación diferencial de la carga de un circuito RC que vimos en este post anterior.

Si asumimos una frecuencia de reloj de 50MHz tenemos que hacen falta:

$$50000000 * 0.006931471805599453 = 346574 \; ciclos$$

Para esperar desde que el condensador está totalmente descargado hasta que Vo = 1.65v. Como se va a hacer una conversión de 4 bits los puntos de comparación se deberán hacer en los siguientes instantes:

1ª comparación (bit 3): 346574 ciclos de reloj
                           ↓
                      346574 / 2
                           ↓
2ª comparación (bit 2): 173286 ciclos de reloj (instante 519860)
                           ↓
                      173286 / 2
                           ↓
3ª comparación (bit 1):  86643 ciclos de reloj (instante 606503)
                           ↓
                       86643 / 2
                           ↓
4ª comparación (bit 0):  43321 ciclos de reloj (instante 649824)

Tras hacer la 4ª comparación es necesario realizar una descarga completa del condensador para iniciar la siguiente conversión. Si asumimos el peor de los casos, que el condensador esté totalmente cargado (Vo(0) = 3.3v), tenemos que para llegar a Vo = 0.01v con Vi = 0 se necesitan:

$$-10000 \times 0.000001 \times log\left({{0.01 - 0} \over {3.3 - 0}}\right) = 0.057990926544605255 \; segundos$$

Que equivalen a:

$$50000000 \times 0.057990926544605255 = 2899546 \; ciclos$$

Desde un punto de vista teórico el condensador nunca se descarga del todo (siempre tiene carga residual). Si se pusiese 0 en lugar 0.01 en la ecuación anterior el tiempo tendería a infinito, por lo que hay que poner una cantidad muy baja que no sea cero. De forma global se ve que cada conversión requiere:

649824 ciclos para la conversión en sí + 2899546 ciclos para descargar el condensador del todo antes de iniciar una nueva conversión = 3549370 ciclos

Para contar 3549370 ciclos (desde 0 hasta 3549369) hacen falta como mínimo 22 bits ($2^{21} = 2097152$, se queda corto, y $2^{22} = 4194304$). Por tanto el "motor" de nuestro conversor analógico-digital de 4 bits será un contador de 22 bits que emitirá las siguientes señales de control:

     0 --> forzar biestable de comparación = 1

346574 --> cargar el biestable con el 1º valor de comparación
346575 --> empujar valor biestable en registro de desplazamiento (bit 3)

519860 --> cargar el biestable con el 2º valor de comparación
519861 --> empujar valor biestable en registro de desplazamiento (bit 2)

606503 --> cargar el biestable con el 3º valor de comparación
606504 --> empujar valor biestable en registro de desplazamiento (bit 1)

649824 --> cargar el biestable con el 4º valor de comparación
649825 --> empujar valor biestable en registro de desplazamiento (bit 0)
           forzar biestable de comparación = 1
649826 --> cargar registro de salida desde registro de desplazamiento

El proceso de descarga se realizará entre el ciclo 649825 y el 4194303 ($2^{22} - 1$). No se va a reiniciar el contador en el ciclo 3549370 para evitar sobrecargar con más puertas lógicas el diseño, sino que se va a dejar que el contador se desborde de forma natural en el ciclo 4194304 ($2^{22}$). Se pierde una centésima de segundo en resolución temporal pero para el caso que nos ocupa no es relevante. Aprovechar el mismo registro contador de tiempo como máquina de estados simplifica enormemente el diseño.



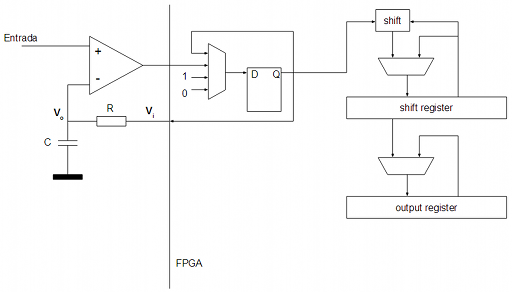
La implementación en VHDL partiendo de este diagrama es muy sencilla:


Conclusión

Usar un registro de aproximaciones sucesivas (SAR) es la forma más sencilla y barata de implementar un ADC, aunque tiene sus inconvenientes:

- Las conversiones son lentas. Aunque pongamos condensadores y resistencias pequeños, es complicado aumentar la frecuencia de muestreo por encima de unos pocos KHz.

- La pendiente de carga de un condensador en un circuito típico RC no es lineal por lo que la conversión resultante tampoco será lineal. Este escollo puede superarse con un circuito externo más elaborado que garantice una corriente de carga constante en el condensador y, por tanto, una pendiente de carga constante en el mismo.

También tiene sus ventajas :-):

- Usa relativamente pocos recursos de la FPGA.
Muy pocos componentes externos. El comparador podría implementarse incluso utilizando las entradas diferenciales que todas las FPGAs tienen (LVDS, mini-LVDS, etc.).

- La resolución en bits es arbitraria y sólo depende de la implementación interna en la FPGA.

A continuación puede verse un vídeo con el conversor implementado al que se le han conectado cuatro leds:



Todo el código puede descargarse de la sección soft.

[ añadir comentario ] ( 1534 visualizaciones )   |  [ 0 trackbacks ]   |  enlace permanente  |   ( 3 / 5055 )

---

A lo largo de este post se desarrollará el cálculo de la curva de carga de un condensador en una red RC estándar: se trata de un post muy cortito pero intenso y espero que interesante. Se va a hacer una aproximación desde cero, planteando el problema inicial, las ecuaciones y obteniendo la solución tanto de forma analítica como numérica.

El circuito

Partimos de un circuito estándar RC. En el que R, C y $V_i$ son constantes. El objetivo es calcular la curva de la salida $V_o$ con respecto al tiempo:



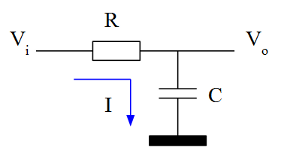
La ecuación

Si asumimos que a través de la salida no se consume corriente, la corriente que circula por la resistencia:
$$I={V_i - V_o \over R}$$
Será igual a la corriente que circula por el condensador:
$$I=C{dV_o \over dt}$$
Igualando ambas expresiones obtenemos la ecuación básica de este circuito:
$${V_i - V_o \over R}=C{dV_o \over dt} \Rightarrow {V_i \over RC} - {V_o \over RC}={dV_o \over dt}$$

Solución analítica

Se trata de una ecuación diferencial lineal de primer orden:
$$y^\prime+p(x)y=q(x)$$
$$ y(x_0)=y_0 $$
Ya que si cambiamos el orden de los operandos:
$${dV_o \over dt}+{1 \over RC}V_o={V_i \over RC}$$
Se ve fácilmente que:
$$y=V_o$$
$$x=t$$
$$p(x)={1 \over RC}$$
$$q(x)={V_i \over RC}$$
Por tanto se puede calcular en valor de $V_o$ en función de $t$ usando la forma estándar de resolución de este tipo de ecuaciones diferenciales:
$$V_o=e^{-\int_{0}^{t}p(s)ds}\left[ V_o(0)+\int_{0}^{t}q(s)e^{\int_{0}^{s}p(v)dv}ds\right]$$
Siendo $V_o(0)$ el valor de $V_o$ en el instance inicial (0 si el condensador está totalmente descargado). Como tenemos que:
$$\int_{0}^{w}p(t)dt=\int_{0}^{w}{1 \over RC}dt={1 \over RC}\int_{0}^{w}dt={1 \over RC}\left[t\right]_{0}^{w}={w \over RC}$$
Entonces podemos reescribir la ecuación de $V_o$ como:
$$V_o=e^{-{t \over RC}}\left[V_o(0)+\int_{0}^{t}{V_i \over RC}e^{s \over RC}ds\right]$$
Calculando la integral de dentro tenemos que:
$$\int_{0}^{t}{V_i \over RC}e^{s \over RC}ds={V_i \over RC}\int_{0}^{t}e^{s \over RC}ds={V_i \over RC}\left[RCe^{s \over RC}\right]_{0}^{t}={V_i \over RC}\left(RCe^{t \over RC}-RCe^0\right)=V_i\left(e^{t \over RC}-1\right)$$
Sustituyendo ahora la integral por su resultado, la ecuación $V_o$ la podemos reescribir de la siguiente manera:
$$V_o=e^{-{t \over RC}}\left(V_o(0)+V_i\left(e^{t \over RC}-1\right)\right)=e^{-{t \over RC}}V_o(0)+e^{-{t \over RC}}V_i\left(e^{t \over RC}-1\right)$$
$$V_o=e^{-{t \over RC}}V_o(0)+V_i\left(e^{-{t \over RC}}e^{t \over RC}-e^{-{t \over RC}}\right)=e^{-{t \over RC}}V_o(0)+V_i\left(1-e^{-{t \over RC}}\right)$$
Con lo que nos sale:
$$V_o=e^{-{t \over RC}}V_o(0)+V_i\left(1-e^{-{t \over RC}}\right)$$
Nótese que si despejamos la $t$ se puede saber el tiempo que tarda el condensador en alcanzar un voltaje final $V_o$ partiendo de un voltaje de salida inicial $V_o(0)$ y con un voltaje de entrada de $V_i$:
$$t=-RC\log\left({V_o-V_i \over V_o(0)-V_i}\right)$$

Solución numérica

Para obtener una solución numérica lo que hacemos en este caso es despejar la derivada de la salida en la ecuación inicial:
$${dV_o \over dt}={V_i \over RC}-{V_o \over RC}={V_i-V_o \over RC}$$
Por lo tanto la salida $V_o$ en el instante $t=s$ será:
$$V_o=\int_{0}^{s}{V_i-V_o \over RC}dt$$
Esta integral definida podemos aproximarla mediante un método de integración numérica. En este caso, por simplicidad, optaremos por uno de los métodos de integración numérica más sencillos: el método de Euler. Según este método, si tenemos que:
$${dy \over dx}=f(x,y)$$
Entonces $y$ lo podemos aproximar mediante la siguiente ecuación de recurrencia:
$$y_n=y_{n-1}+h \times f(x_{n-1},y_{n-1})$$
Siendo $h$ un valor que tiende a cero. En el caso que nos ocupa:
$$y=V_o$$
$$x=t$$
$$f(t,V_o)={V_i-V_o \over RC}$$
Por lo tanto la ecuación de recurrencia del método de Euler quedaría como sigue:
$$V_{o_n}=V_{o_{n-1}}+h \times {V_i-V_{o_{n-1}} \over RC}$$
Las condiciones iniciales vendrán determinadas, al igual que la solución analítica por el valor de $V_o$ cuando $n=0$.

Representación de ambas soluciones

A continuación puede verse un código en lenguaje Octave (software libre de cálculo numérico) que pinta superpuestas las gráficas resultantes de ambas soluciones asumiento con condiciones iniciales nulas ($V_o=0$, i.e. condensador totalmente descargado, en el instante inicial).


La solución analítica es la más exacta pero también es la más complicada de obtener ya que requiere del uso de ecuaciones diferenciales mientras que la solución numérica no es la más exacta pero es más sencilla de obtener.



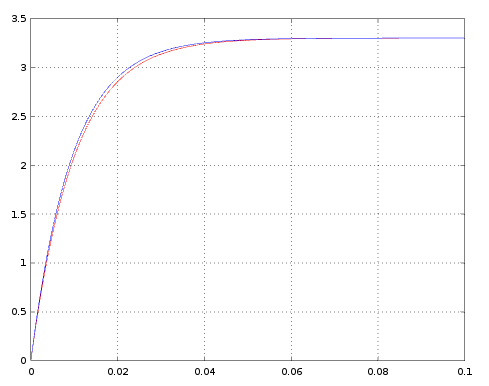
En rojo puede verse la solución analítica y en azul la solución numérica. Hay que tener en cuenta que se ha utilizado el método de Euler de integración numérica que no es, ni de lejos, de los mejores métodos de integración. Con otros métodos de integración, como el Runge-Kutta de cuarto orden (RK4) se obtendrían resultados mucho mejores y con un error mucho menor con respecto de la solución analítica.

Espero que les haya resultado interesante.

[ 3 comentarios ] ( 41903 visualizaciones )   |  [ 0 trackbacks ]   |  enlace permanente  |   ( 3 / 4571 )

---

<< <Anterior | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | Siguiente> >>

- Página generada en 0.2619 segundos | Site Views: 172669