Plano z
La herramienta fundamental para el cálculo de filtros digitales es la transformada Z y su plano complejo asociado, denominado "plano z". Se asume que el lector está medianamente familiarizado con la transformada z y no se abordarán los detalles ni las propiedades de la misma.
La transformada z transforma una función, situada en el dominio discreto del tiempo $x[n]$, en otra función, situada en el dominio complejo de z $X(z)$. Esta transformación es equivalente a la transformada de Laplace en el dominio continuo y tiene ambas propiedades similares en cuanto a linealidad y estabilidad. Al igual que la transformada de Laplace, la transformada Z también se utiliza para modelar funciones de transferencia de sistemas, en el caso de la transformada Z, son sistemas discretos.
Es decir, si para un filtro analógico tenemos una función de transferencia $H(s)$, caracterizada principalmente por sus ceros y sus polos, para un filtro digital tendremos también una función de transferencia $H(z)$, caracterizada también por sus ceros y sus polos. Tanto en el caso de Laplace como en el caso Z los ceros determinan para qué tipo de señales el filtro "tiende a cancelar la entrada" y los polos determinan para qué tipo de señales el filtro "tiende a amplificar la entrada" o incluso entrar en resonancia. La regla básica que debe cumplirse en un filtro analógico es que los polos de $H(s)$ nunca deben tener parte real positiva (deben estar siempre localizados en el semiplano izquierdo del plano complejo $s$), mientras que en caso de un filtro digital, los polos de $H(z)$ nunca deben alojarse fuera de la circunferencia unitaria centrada en el origen del plano complejo $z$ (es decir, los polos en un filtro digital deben cumplir que $|z| < 1$).
Diseño de un filtro resonante sencillo
En el plano z no se mapean frecuencias absolutas como en el plano s, sino que se mapean frecuencias "relativas" a la frecuencia de muestreo y a lo largo de la longitud de la circunferencia de radio 1. La frecuencia asociada a un valor complejo del plano z se corresponde con el ángulo (argumento) de dicho valor: un ángulo de 0 radianes se corresponde con un valor en continua (0 Hz) mientras que un valor de $\pi$ radianes se corresponde con la mitad de la frecuencia de muestreo (frecuencia Nyquist). Si, por ejemplo, muestreamos a 44100 Hz, la frecuencia máxima ($\pi$) será de 22050 Hz, mientras que si muestreamos a 8000 Hz la misma frecuencia PI se corresponderá con 4000 Hz.
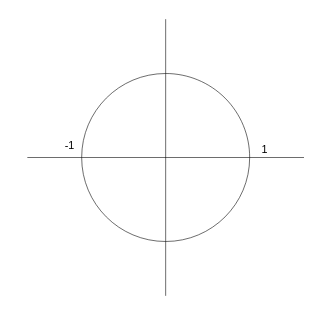
El diseño básico de filtros digitales es muy sencillo y se resume en cuatro reglas principales:
- Alojar tantos ceros sobre la circunferencia de radio 1 como frecuencias queramos cancelar. Lo importante de cada cero será su ángulo (= frecuencia) con respecto al origen. Por ejemplo si colocamos un cero en en punto $z = 1$, que se corresponde con un ángulo de 0 radianes, nuestro filtro eliminará la componente de continua de la señal.
- Alojar tantos polos DENTRO de la circunferencia de radio 1 ($|z| < 1$) como frecuencias queramos amplificar. En este caso es importante tanto el ángulo (= frecuencia que queremos reforzar) como su magnitud o módulo (= nivel de refuerzo). Si hacemos que la magnitud (el módulo) de un polo sea 1 ($|z| = 1$) el filtro auto-oscilará a esa frecuencia. Por ejemplo, si colocamos un polo en $z = -1$, que se corresponde con un ángulo $\pi$, estaremos reforzando las señales con frecuencia próxima a $\pi$ (= la mitad de la frecuencia de muestreo).
- Los polos y ceros que tengan parte imaginaria diferente de 0 deberán ponerse por pares conjugados para poder trabajar con señales reales (sin componente imaginaria). Por ejemplo, si estamos muestreando a 44100 Hz y queremos cancelar las frecuencias próximas a 11025 Hz (frecuencia ${\pi \over 2}$), debemos colocar DOS polos conjugados: uno en $(0, 1)$, formando un ángulo de 90 grados (${\pi \over 2}$) y otro en $(0, -1)$ (su conjugado).
- Al final lo habitual es también ajustar la ganancia global del filtro (aunque en este caso no lo hemos hecho por simplicidad). Esto se hace habitualmente debido a que a veces los polos meten mucha ganancia en la banda de paso y es necesario escalar la salida antes de emitirla o la entrada antes de procesarla.
Si, por ejemplo, queremos hacer un filtro paso bajo, lo habitual, es poner un cero en $z = -1$ (sobre la circunferencia de radio 1 con ángulo $\pi$) con el objetivo de anular las altas frecuencias y un polo (con su complejo conjugado) cerca de la frecuencia de corte de nuestro filtro. En nuestro caso de estudio, se trata de un filtro resonante sencillo, por lo que definiremos dos ceros: uno en $z = 1$ (0 radianes), y otro en $z = -1$, ($\pi$ radianes). Como queremos una única frecuencia de resonancia, definimos un único polo (junto con su complejo conjugado, por lo que realmente serán dos polos).
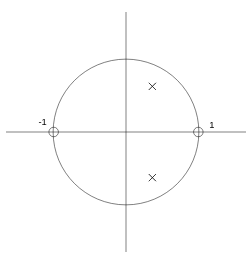
Con esta configuración de dos ceros reales en -1 y 1 y dos polos complejos conjugados en la frecuencia de resonancia tenemos la siguiente función de transferencia en Z:
$$H(z) = {(z + 1)(z - 1) \over (z - p_1)(z - p_1^\prime)}$$
Para la que se cumple que:
$$p_1 = a + bi \;\;\;\;\;\;\;\;\; p_1^\prime = a - bi$$
Desarrollando el denominador (los polos) de $H(z)$ tenemos que:
$$(z - p_1)(z - p_1^\prime) = z(z - p_1^\prime) - p_1(z - p_1^\prime)$$
$$ = z^2 - zp_1^\prime -p_1z + p_1p_1^\prime$$
$$ = z^2 - z(p_1^\prime + p_1) + p_1p_1^\prime$$
$$ = z^2 - z2a + p_1p_1^\prime$$
$$ = z^2 - z2a + a^2 + b^2$$
Nótese que, al ser los polos complejos conjugados, las operaciones
$(p_1^\prime + p_1)$ y $p_1p_1^\prime$ dan como resultado, valores reales (sin componente imaginaria). Por otro lado, si desarrollamos el numerador (los ceros) de $H(z)$ tenemos que:
$$(z + 1)(z - 1) = z(z - 1) + (z - 1)$$
$$ = z^2 - z + z - 1$$
$$ = z^2 - 1$$
Por tanto la función de transferencia $H(z)$ puede reescribirse de la siguiente manera:
$$H(z) = {{z^2 - 1} \over {z^2 - z2a + a^2 + b^2}}$$
Podemos visualizar la respuesta en frecuencia de este sistema asignando a z diferentes valores sobre la circunferencia unitaria $z = e^{iw} = cos(w) + i sen(w)$:
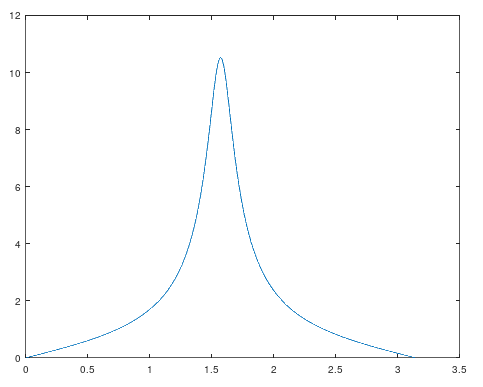
Para generar esta gráfica se ejecutó el siguiente código octave que sitúa el polo (= la frecuencia de resonancia del filtro) en ${\pi \over 2}$:
m = 0.9; w = pi / 2; a = m * cos(w); b = m * sin(w); # respuesta en frecuencia TAM = 1000; responseX = zeros(1, TAM); responseY = zeros(1, TAM); for n = 1:TAM w = (n / TAM) * pi; responseX(n) = w; z = cos(w) + (i * sin(w)); responseY(n) = abs(((z * z) - 1) / ((z * z) - (z * 2 * a) + (a * a) + (b * b))); endfor plot(responseX, responseY);
Implementación del filtro
Ahora que ya tenemos la función de transferencia en el dominio Z del filtro que queremos, el siguiente paso es pasar al dominio discreto y calcular los coeficientes en diferencias finitas para poder implementarlo. Lo primero que se hace es evitar que haya exponentes mayores que 0 para z (exponentes positivos de z se corresponden a muestras "futuras" en el tiempo). Esto se soluciona de forma muy sencilla multiplicando numerador y denominador de $H(z)$ por $z^{-2}$, esto mantiene $H(z)$ igual pero elimina los exponentes positivos:
$$H(z) = {{z^2 - 1} \over {z^2 - z2a + a^2 + b^2}}$$
$$H(z) = {{z^{-2}(z^2 - 1)} \over {z^{-2}(z^2 - z2a + a^2 + b^2)}}$$
$$H(z) = {{1 - z^{-2}} \over {1 - z^{-1}2a + z^{-2}(a^2 + b^2)}}$$
Ahora ya podemos calcular los coeficientes de forma más sencilla. Como $H(z)$ es una función de transferencia en Z tenemos que, si $X(z)$ es la transformada Z de la entrada e $Y(z)$ es la transformada Z de la salida, entonces:
$$Y(z) = H(z) X(z) = {{1 - z^{-2}} \over {1 - z^{-1}2a + z^{-2}(a^2 + b^2)}} X(z)$$
Y, por tanto:
$$Y(z)(1 - z^{-1}2a + z^{-2}(a^2 + b^2)) = X(z)(1 - z^{-2})$$
$$Y(z)-Y(z)z^{-1}2a+Y(z)z^{-2}(a^2 + b^2) = X(z) - X(z)z^{-2}$$
Como la transformada Z es lineal y se cumple que la transformada Z de un valor desplazado k muestras en el tiempo es la siguiente:
$$Z \left\{ x[n - k] \right\} = X(z)z^{-k}$$
Entonces podemos hacer la antitransformada Z de forma sencilla:
$$y[n] - y[n - 1]2a + y[n - 2](a^2 + b^2) = x[n] - x[n - 2]$$
Y, despejando $y[n]$ tenemos que:
$$y[n] = x[n] - x[n - 2] + y[n - 1]2a - y[n - 2](a^2 + b^2)$$
Esto, como se puede ver, es una ecuación en diferencias finitas, que es muy fácil de implementar tanto en hardware como en software. Veamos una ejemplo de código octave que genera ruido blanco y luego lo hace pasar por el filtro (aplica la ecuación en diferencias finitas con los mismos valores a y b, esto es, misma frecuencia de resonancia en ${\pi \over 2}$).
m = 0.9; w = pi / 2; a = m * cos(w); b = m * sin(w); TAM = 1000; input = (rand(1, N) .* 2) .- 1; # TAM valores aleatorios entre -1 y 1 ym1 = 0; ym2 = 0; xm1 = 0; xm2 = 0; output = zeros(1, TAM); for n = 1:TAM output(n) = input(n) - xm2 + (ym1 * 2 * a) - (ym2 * ((a * a) + (b * b))); ym2 = ym1; ym1 = output(n); xm2 = xm1; xm1 = input(n); endfor subplot(2, 2, 1) plot(input); title('Ruido'); subplot(2, 2, 2) plot(output); title('Ruido filtrado'); subplot(2, 2, 3) plot(abs(fft(input)(1:(N / 2)))); title('Espectro del ruido'); subplot(2, 2, 4) plot(abs(fft(output)(1:(N / 2)))); title('Espectro del ruido filtrado');
A continuación se pueden ver las señales y los espectros en frecuencia de las mismas y se puede comprobar como el funcionamiento del filtro es el esperado:
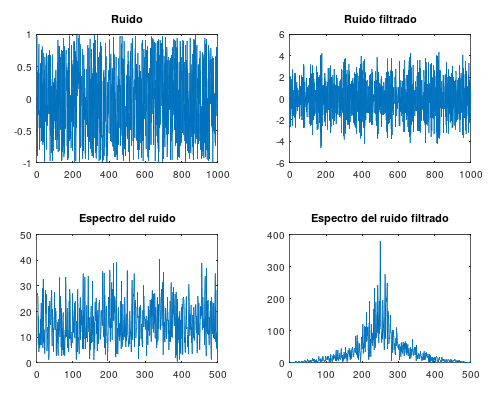
[ añadir comentario ] ( 2780 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 2725 )
( 3 / 2725 )
 Calendario
Calendario




