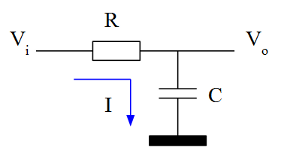
El circuito
Partimos de un circuito estándar RC. En el que R, C y $V_i$ son constantes. El objetivo es calcular la curva de la salida $V_o$ con respecto al tiempo:
La ecuación
Si asumimos que a través de la salida no se consume corriente, la corriente que circula por la resistencia:
$$I={V_i - V_o \over R}$$
Será igual a la corriente que circula por el condensador:
$$I=C{dV_o \over dt}$$
Igualando ambas expresiones obtenemos la ecuación básica de este circuito:
$${V_i - V_o \over R}=C{dV_o \over dt} \Rightarrow {V_i \over RC} - {V_o \over RC}={dV_o \over dt}$$
Solución analítica
Se trata de una ecuación diferencial lineal de primer orden:
$$y^\prime+p(x)y=q(x)$$
$$ y(x_0)=y_0 $$
Ya que si cambiamos el orden de los operandos:
$${dV_o \over dt}+{1 \over RC}V_o={V_i \over RC}$$
Se ve fácilmente que:
$$y=V_o$$
$$x=t$$
$$p(x)={1 \over RC}$$
$$q(x)={V_i \over RC}$$
Por tanto se puede calcular en valor de $V_o$ en función de $t$ usando la forma estándar de resolución de este tipo de ecuaciones diferenciales:
$$V_o=e^{-\int_{0}^{t}p(s)ds}\left[ V_o(0)+\int_{0}^{t}q(s)e^{\int_{0}^{s}p(v)dv}ds\right]$$
Siendo $V_o(0)$ el valor de $V_o$ en el instance inicial (0 si el condensador está totalmente descargado). Como tenemos que:
$$\int_{0}^{w}p(t)dt=\int_{0}^{w}{1 \over RC}dt={1 \over RC}\int_{0}^{w}dt={1 \over RC}\left[t\right]_{0}^{w}={w \over RC}$$
Entonces podemos reescribir la ecuación de $V_o$ como:
$$V_o=e^{-{t \over RC}}\left[V_o(0)+\int_{0}^{t}{V_i \over RC}e^{s \over RC}ds\right]$$
Calculando la integral de dentro tenemos que:
$$\int_{0}^{t}{V_i \over RC}e^{s \over RC}ds={V_i \over RC}\int_{0}^{t}e^{s \over RC}ds={V_i \over RC}\left[RCe^{s \over RC}\right]_{0}^{t}={V_i \over RC}\left(RCe^{t \over RC}-RCe^0\right)=V_i\left(e^{t \over RC}-1\right)$$
Sustituyendo ahora la integral por su resultado, la ecuación $V_o$ la podemos reescribir de la siguiente manera:
$$V_o=e^{-{t \over RC}}\left(V_o(0)+V_i\left(e^{t \over RC}-1\right)\right)=e^{-{t \over RC}}V_o(0)+e^{-{t \over RC}}V_i\left(e^{t \over RC}-1\right)$$
$$V_o=e^{-{t \over RC}}V_o(0)+V_i\left(e^{-{t \over RC}}e^{t \over RC}-e^{-{t \over RC}}\right)=e^{-{t \over RC}}V_o(0)+V_i\left(1-e^{-{t \over RC}}\right)$$
Con lo que nos sale:
$$V_o=e^{-{t \over RC}}V_o(0)+V_i\left(1-e^{-{t \over RC}}\right)$$
Nótese que si despejamos la $t$ se puede saber el tiempo que tarda el condensador en alcanzar un voltaje final $V_o$ partiendo de un voltaje de salida inicial $V_o(0)$ y con un voltaje de entrada de $V_i$:
$$t=-RC\log\left({V_o-V_i \over V_o(0)-V_i}\right)$$
Solución numérica
Para obtener una solución numérica lo que hacemos en este caso es despejar la derivada de la salida en la ecuación inicial:
$${dV_o \over dt}={V_i \over RC}-{V_o \over RC}={V_i-V_o \over RC}$$
Por lo tanto la salida $V_o$ en el instante $t=s$ será:
$$V_o=\int_{0}^{s}{V_i-V_o \over RC}dt$$
Esta integral definida podemos aproximarla mediante un método de integración numérica. En este caso, por simplicidad, optaremos por uno de los métodos de integración numérica más sencillos: el método de Euler. Según este método, si tenemos que:
$${dy \over dx}=f(x,y)$$
Entonces $y$ lo podemos aproximar mediante la siguiente ecuación de recurrencia:
$$y_n=y_{n-1}+h \times f(x_{n-1},y_{n-1})$$
Siendo $h$ un valor que tiende a cero. En el caso que nos ocupa:
$$y=V_o$$
$$x=t$$
$$f(t,V_o)={V_i-V_o \over RC}$$
Por lo tanto la ecuación de recurrencia del método de Euler quedaría como sigue:
$$V_{o_n}=V_{o_{n-1}}+h \times {V_i-V_{o_{n-1}} \over RC}$$
Las condiciones iniciales vendrán determinadas, al igual que la solución analítica por el valor de $V_o$ cuando $n=0$.
Representación de ambas soluciones
A continuación puede verse un código en lenguaje Octave (software libre de cálculo numérico) que pinta superpuestas las gráficas resultantes de ambas soluciones asumiento con condiciones iniciales nulas ($V_o=0$, i.e. condensador totalmente descargado, en el instante inicial).
global R = 10000; % R = 10 K global C = 0.000001; % C = 1 uF global Vi = 3.3; % Vi = 3.3 voltios global h = 0.001; global t = [0:h:0.1]; % entre 0 y 0.1 segundos con pasos de h = 0.001 segundos % solución analítica con condiciones iniciales nulas Vo_analytic = Vi * (1 - exp(-t ./ (R * C))); % solución numérica function ret = f(Vo) global R; global C; global Vi; ret = (Vi - Vo) / (R * C); endfunction Vo_numeric = zeros(size(t)); n = 1; for i = t if (n == 1) Vo_numeric(1) = 0; % condiciones iniciales nulas else % integramos numéricamente mediante el método de Euler Vo_numeric(n) = Vo_numeric(n - 1) + h * f(Vo_numeric(n - 1)); endif n = n + 1; endfor % visualizamos ambas soluciones (en rojo la solución analítica y en azul la solución numérica) plot(t, Vo_analytic, "r", t, Vo_numeric, "b");
La solución analítica es la más exacta pero también es la más complicada de obtener ya que requiere del uso de ecuaciones diferenciales mientras que la solución numérica no es la más exacta pero es más sencilla de obtener.
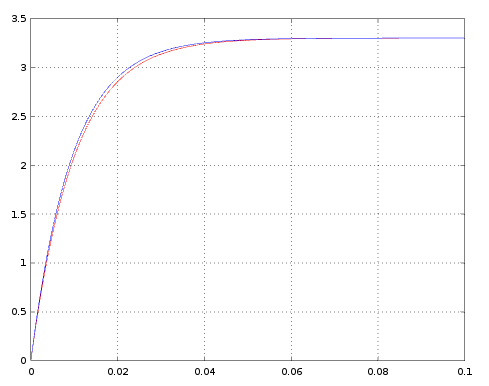
En rojo puede verse la solución analítica y en azul la solución numérica. Hay que tener en cuenta que se ha utilizado el método de Euler de integración numérica que no es, ni de lejos, de los mejores métodos de integración. Con otros métodos de integración, como el Runge-Kutta de cuarto orden (RK4) se obtendrían resultados mucho mejores y con un error mucho menor con respecto de la solución analítica.
Espero que les haya resultado interesante.
[ 3 comentarios ] ( 43513 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 6437 )
( 3 / 6437 )
 Calendario
Calendario




