El DAC de Texas Instruments PCM5102 es un DAC que soporta el estándar I2S de transferencia de audio digital y el estándar “left justified” (variante del I2S). Existen muchos otros DACs de audio en el mercado con soporte para estos formatos, sin embargo los más usados son el ES9023 y derivados, de ESS, y el PCM5102 y derivados, de Texas Instruments. En mi caso, adquirí una placa con un integrado PCM5102A y la circuitería mínima (componentes pasivos, espadines para conectar alimentación y las tres líneas del protocolo I2S y dos conectores RCA hembra de salida, uno para cada canal).

Unos 14€ por AliExpress (gastos de envío incluidos), aunque ahora creo que está incluso más barato.
I2S
El protocolo I2S es un protocolo muy sencillo de transferencia de audio digital. Aunque por su nombre puede parecer que es un protocolo derivado o parecido al protocolo I2C, lo cierto es que sólo se parecen en el nombre y, para nuestro alivio, es bastante más sencillo que el I2C.
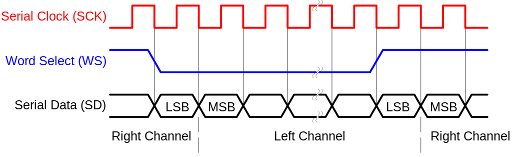
(imagen extraida de Wikimedia, realizada por el usuario Wdwd y con licencia Creative Commons Attribution 3.0 Unported)
El protocolo, como se puede ver en el diagrama, solo necesita de tres hilos: uno para datos, otro para el reloj y otro para seleccionar la palabra o el frame (ponemos esta señal a 0 para enviar la muestra del canal izquierdo y a 1 para enviar la muestra del canal derecho).
Al tratarse de un protocolo de transferencia serie, si queremos emitir audio con calidad CD (16 bits a 44100 Hz estéreo) hace falta generar un reloj de:
$$44100 \times 16 \times 2 = 1411200 \thinspace Hz$$
Como se puede ver, si se quiere trabajar con frecuencias de muestreo lo suficientemente altas como para asegurar una mínima calidad de audio, es necesario hardware dedicado: generar esas señales por software es muy ineficiente. En nuestro caso el microcontrolador MK20 de Freescale (ARM Cortex-M4) que viene en la placa Teensy sí que viene equipado con un interface I2S totalmente programable.
El interface I2S en el microcontrolador MK20
El interface I2S tiene dos modos: directo y mediante DMA. En esta primera aproximación he implementado el modo directo (sin DMA). Es el modo que más CPU consume pero también es el más sencillo. Los pasos para configurar la interface de salida I2S en el MK20 son, grosso modo, los siguientes:
1. Configurar el multiplexor de pines para asignar las tres señales a pines reales.
2. Configurar el los divisores de frecuencia para obtener el “bit clock” de I2S a partir del reloj del sistema.
3. Configurar el tamaño de palabra (16 bits estéreo en nuestro caso).
4. Colgar de la IRQ 35 la función encargada de escribir las muestras en el registro de datos I2S.
5. Habilitar la IRQ 35 (vector de interrupción 16 + 35 = 51 del ARM Cortex-M4).
Configurar el multiplexor de pines es muy sencillo. En este caso he optado por usar la configuración “ALT6” para los pines PORTA.12, PORTA.13 y PORTC.3 que les dan la funcionalidad TX, FS (frame select, el equivalente a "word select") y BCLK (bit clock) respectivamente.
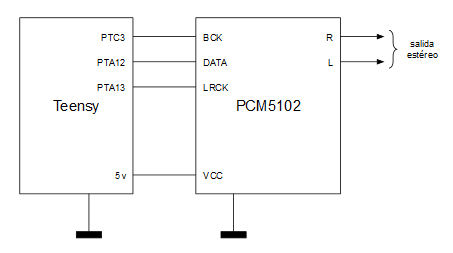
Para configurar el BCLK se dispone de un divisor de frecuencia fraccionario y de un divisor de frecuencia entero. Si quisiéramos usar una frecuencia de muestreo de 48KHz haríamos los siguiente:
1. Establecemos como fuente de reloj, el reloj del núcleo (SYSCLK) que, en nuestro caso, va a 96 MHz.
2. El divisor de frecuencia fraccionario lo configuramos con el valor: 16 / 125 (96 * 16 / 125 = 12.288 MHz).
3. El divisor de frecuencia entero lo configuramos a continuación con el valor 8: 12.288 / 8 = 1.536 MHz).
En este caso: 48 KHz * 2 * 16 = 1.536 MHz.
El resto de pasos es mejor verlos en el código:
bool i2sInit() { // configure i/o pins // (PTA12 = TX, PTA13 = FS, PTC3 = BCLK) --> ALT6 PORTA_PCR12 = ((uint32_t) 6) << 8; PORTA_PCR13 = ((uint32_t) 6) << 8; PORTC_PCR3 = ((uint32_t) 6) << 8; // enable system clock for i2s module SIM_SCGC6 |= ((uint32_t) 1) << 15; // select input clock 0 and output enable I2S0_MCR = ((uint32_t) 1) << 30; #if (I2S_SAMPLE_RATE == 48000) // divide to get the 12.2880 MHz from 96MHz (96 * (16/125)) I2S0_MDR = (((uint32_t) 15) << 12) | ((uint32_t) 124); #elif (I2S_SAMPLE_RATE == 44100) // divide to get the 11.2896 MHz from 96MHz (96 * (2/17)) I2S0_MDR = (((uint32_t) 1) << 12) | ((uint32_t) 16); #elif (I2S_SAMPLE_RATE == 32050) // divide to get the 8.2051 MHz from 96MHz (96 * (10/117)) I2S0_MDR = (((uint32_t) 9) << 12) | ((uint32_t) 116); #else #error "I2S_SAMPLE_RATE must be 48000, 44100 or 32050" #endif // re-enable system clock to the i2s module SIM_SCGC6 |= ((uint32_t) 1) << 15; // disable tx (TE=0) while configuring I2S0_TCSR &= ~(((uint32_t) 1) << 31); // transmitter remains enabled until (and TE set) the end of the current frame for (int i = 0; (i < 1000) && (I2S0_TCSR & (((uint32_t) 1) << 31)); i++) ; if (I2S0_TCSR & (((uint32_t) 1) << 31)) return false; // no word mask I2S0_TMR = 0; // set FIFO watermark I2S0_TCR1 = ((uint32_t) (I2S_FRAME_SIZE - 1)); // use asynchronous mode (SYNC=0), BCLK polatiry active low (BCP=0), select master clock 1 (MSEL=1), bit clock divide (DIV=3), BCLK internally generated I2S0_TCR2 = (((uint32_t) 1) << 25) | (((uint32_t) 1) << 26) | ((uint32_t) 3) | (((uint32_t) 1) << 24); // transmit data channel is enabled (TCE=1) I2S0_TCR3 = (((uint32_t) 1) << 16); // frame size (FRSZ), bits per frame sync (SYWD), MSB (MF=1), I2S standard (not "left justified") (FSE=1), frame sync in master mode (FSD) I2S0_TCR4 = (((uint32_t) (I2S_FRAME_SIZE - 1)) << 16) | (((uint32_t) (I2S_IO_BIT_DEPTH - 1)) << 8) | (((uint32_t) 1) << 4) | (((uint32_t) 1) << 3) | ((uint32_t) 1); // bits per word for first word in each frane (W0W), bits per word for rest of words in each frame (WNW), bit index for first bit tx (MSB, 15-th for 16 bit) //I2S0_TCR5 = (((uint32_t) (I2S_IO_BIT_DEPTH - 1)) << 16) | (((uint32_t) (I2S_IO_BIT_DEPTH - 1)) << 24) | (((uint32_t) 15) << 8); I2S0_TCR5 = (((uint32_t) (I2S_IO_BIT_DEPTH - 1)) << 16) | (((uint32_t) (I2S_IO_BIT_DEPTH - 1)) << 24) | (((uint32_t) (I2S_IO_BIT_DEPTH - 1)) << 8); return true; } void i2sStart() { wavePtr = (int16_t *) &_binary_drum_loop_16_raw_start; NVIC_ENABLE_IRQ(IRQ_I2S0_TX); // tx enable (TE=1), bit clock enable (BCE=1), FIFO request interrupt enable, FIFO reset I2S0_TCSR |= (((uint32_t) 1) << 31) | (((uint32_t) 1) << 28) | (((uint32_t) 1) << 8) | (((uint32_t) 1) << 25); } void i2sStop() { NVIC_DISABLE_IRQ(IRQ_I2S0_TX); }
Además de lo dicho, es necesario colgar de la IRQ 35 una rutina que será invocada tantas veces por segundo como indique la frecuencia de muestreo y que será la encargada de escribir en el registro de salida I2S las muestras de audio que se van a emitir por la interface I2S. Definimos la rutina de la siguiente manera dentro del codigo C++:
extern char _binary_drum_loop_16_raw_start; extern char _binary_drum_loop_16_raw_end; volatile char *p; void i2sTx() __attribute__ ((section(".i2s_tx"))); volatile int16_t *wavePtr; void i2sTx() { // if FRF=0, return if (!(I2S0_TCSR & (((uint32_t) 1) << 16))) return; // write left and right sample I2S0_TDR0 = (uint32_t) *wavePtr; I2S0_TDR0 = (uint32_t) *wavePtr; wavePtr++; if (wavePtr >= ((int16_t *) &_binary_drum_loop_16_raw_end)) wavePtr = (int16_t *) &_binary_drum_loop_16_raw_start; // if underrun, clear underrun if (I2S0_TCSR & (((uint32_t) 1) << 18)) I2S0_TCSR |= (((uint32_t) 1) << 18); // if frame sync error, clear frame sync error flag if (I2S0_TCSR & (((uint32_t) 1) << 19)) I2S0_TCSR |= (((uint32_t) 1) << 19); }
Y en el linker script de nuestro proyecto incluimos una seccion especial a la que llamaremos “.cortex_m4_vector_i2s_tx” y que ubicamos en la direccion de memoria 0x000000CC (la correspondiente a la IRQ 35). En esta sección ponemos la dirección de memoria de nuestra rutina de servicio de interrupción (la encargada de escribir las muestras), es decir metemos la dirección de memoria I2S_TX_ADDRESS + 1 (recordar que al tratarse de un Cortex-M, el reportorio de instrucciones es siempre el reportorio “thumb” y, por lo tanto, los destinos de salto para subrutinas y para codigo siempre deben tener su bit 0 a 1).
SECTIONS {
. = 0x00000000 ;
.cortex_m4_vectors : {
LONG(0x20007FFC);
LONG(0x00000411);
}
. = 0x000000CC ;
.cortex_m4_vector_i2s_tx : {
LONG(I2S_TX_ADDRESS + 1);
}
. = 0x00000400 ;
.flash_configuration : {
LONG(0xFFFFFFFF);
LONG(0xFFFFFFFF);
LONG(0xFFFFFFFF);
LONG(0xFFFFFFFE);
}
.text : {
_linker_code = . ;
init.o (.text)
*(.text)
*(.text.*)
*(.rodata*)
*(.gnu.linkonce.t*)
*(.gnu.linkonce.r*)
}
I2S_TX_ADDRESS = . ;
.i2s_tx : {
*(.i2s_tx)
}
.preinit_array : {
__preinit_array_start = . ;
*(.preinit_array)
__preinit_array_end = . ;
}
...resto del linker script...
Audio de ejemplo
Se ha partido de un sample de dominio público consistente en dos golpes de bombo y caja con charles en medio, típicos del estilo de música house. La muestra se emite en 16 bits con una frecuencia de muestreo de 32050 Hz (Se ha usado este frecuencia por razones de espacio en la memoria flash: es una frecuencia que permite reproducir a una calidad buena manteniendo un tamaño lo suficientemente limitado como para caber en la memoria flash del microcontrolador).

Todo el código fuente puede descargarse de la sección soft.
[ añadir comentario ] ( 3309 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 15981 )
( 3 / 15981 )Como cada año por estas fechas hago una revisita al concepto de las luces para el belén usando diferentes tecnologías. En este caso y como no podía ser de otro modo, intentaremos usar una FPGA para implementar este efecto.
Aspectos funcionales
Partimos de 5 leds de alta luminosidad (los mismos de años anteriores) y necesitamos que parpadeen de forma aleatoria, como si simularan el aspecto de una porción del cielo nocturno. La secuencia de parpadeo debería ser lo más aleatoria posible y lo ideal es que la probabilidad de parpadeo sea controlable para simular un ciclo día-noche.
Diseño
Para generar una secuencia de números pseudoaleatorios la forma más sencilla es utilizar un LFSR con la cantidad suficiente de bits como para dar la percepción de que se trata de un generador de números realmente aleatorios. Si partimos de un LFSR de 10 bits, para que sea maximal (que su secuencia numérica sea lo más larga posible antes de “dar la vuelta”) debemos implementar el siguiente polinomio de realimentación:
$$x^{10} + x^7 + 1$$
Este polinomio de realimentación garantiza una secuencia maximal de $2^{n} - 1$ valores, siendo en este caso $n=10$. La secuencia no es de $2^{n}$ valores debido a que el valor 0 (todos los bits a cero) no está incluido en la secuencia.
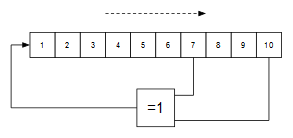
("=1" denota la operación XOR en notación IEC) La ruta de datos que se va a usar es la siguiente:
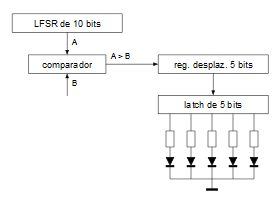
El funcionamiento interno sería el siguiente.
1. Se inicializa el LFSR (se le mete un valor que incluya, al menos un bit a 1).
2. Hacer 5 veces (una vez por cada uno de los 5 leds).
2.1. Se itera el LFSR para que genere el siguiente numero pseudoaleatorio.
2.2. Se empuja el bit resultante de la comparación entre el valor del LFSR (valor A) y una constante (valor B) en el registro de desplazamiento.
3. Se carga en el latch de salida el valor que hay en el registro de desplazamiento.
4. Se espera 1 segundo.
5. Saltar al paso 2.
Tanto para el conteo de la carga de los 5 bits en el registro de desplazamiento como para el conteo del tiempo de espera de 1 segundo se utiliza un contador de 32 bits de dos límites: uno de los límites se fija a 5 (para contar los bits) y otro de los límites se fija en 32000000 para contar 1 segundo (el reloj de la FPGA va a 32MHz).
A partir de este algoritmo se puede diseñar la siguiente máquina de estados:
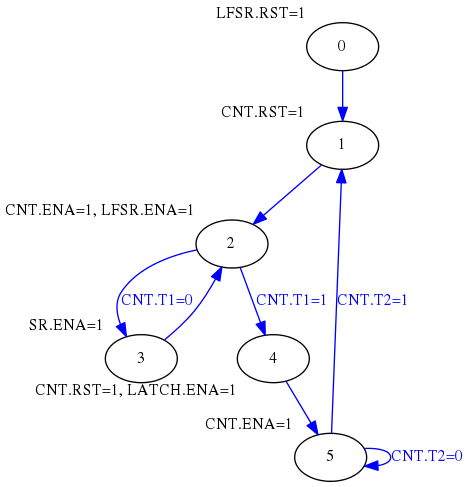
Salidas de la FSM:
LFSR.RST = Reset del LFSR.
LFSR.ENA = Enable del LFSR.
SR.ENA = Enable del registro de desplazamiento.
LATCH.ENA = Enable del latch de salida.
CNT.RST = Reset del contador.
CNT.ENA = Enable del contador.
Entradas de la FSM:
CNT.T1 = a 1 cuando el contador llega a 5.
CNT.T2 = a 1 cuando el contador llega a 32000000.
Como se puede ver, se trata de un diseño totalmente síncrono, basado en enables y en el que se evita el uso de “gated clocks”, por lo tanto, perfectamente sintetizable en cualquier FPGA.
Por ahora la probabilidad de parpadeo está fijada por hardware como una constante (el valor de B en el diagrama, que no es modificable), sin embargo el diseño queda preparado para que en una siguiente versión se pueda obtener dicha constante de algún parámetro físico (ADC, reloj de tiempo real, etc.)
Implementación
La implementacion de todos los módulos se ha realizado siguiendo siempre un modelo RTL. A continuación se lista el codigo fuente de la unidad de más alto nivel (que se ha denominado “ChristmasLights”) y que engloba todos los submódulos (LFSR, comparador, registro de desplazamiento, latch, contador y FSM).
library ieee; use ieee.std_logic_1164.all; use ieee.numeric_std.all; entity ChristmasLights is generic ( NLeds : integer := 8; NWaitClocks : integer := 20; -- for the simulation 20 clocks between lights change, but in real hardware change this value according FPGA clock Probability : integer := 512 -- 0 = all lights on, 1023 = all lights off ); port ( Clk : in std_logic; Reset : in std_logic; Led : out std_logic_vector((NLeds - 1) downto 0) ); end ChristmasLights; architecture Architecture1 of ChristmasLights is component LFSR10 is port ( Reset : in std_logic; Enable : in std_logic; Clk : in std_logic; Data : out std_logic_vector(9 downto 0) ); end component; component Comparator is generic ( NBits : integer := 4 ); port ( A : in std_logic_vector((NBits - 1) downto 0); B : in std_logic_vector((NBits - 1) downto 0); AGreatThanB : out std_logic; ALessThanB : out std_logic; AEqualB : out std_logic ); end component; component ShiftRegister is generic ( NBits : integer := 8 ); port ( Enable : in std_logic; Clk : in std_logic; SerialInput : in std_logic; ParallelOutput : out std_logic_vector((NBits - 1) downto 0) ); end component; component Latch is generic ( NBits : integer := 8 ); port ( Enable : in std_logic; Clk : in std_logic; DataIn : in std_logic_vector((NBits - 1) downto 0); DataOut : out std_logic_vector((NBits - 1) downto 0) ); end component; component TwoLimitCounter is generic ( NBits : integer := 4; Limit1 : integer := 3; Limit2 : integer := 2 ); port ( Reset : in std_logic; Enable : in std_logic; Clock : in std_logic; Terminated1 : out std_logic; Terminated2 : out std_logic ); end component; signal LfsrEnable : std_logic; signal LfsrReset : std_logic; signal LfsrData : std_logic_vector(9 downto 0); signal CompOutput : std_logic; signal SREnable : std_logic; signal SRData : std_logic_vector((NLeds - 1) downto 0); signal LatEnable : std_logic; signal CntReset : std_logic; signal CntEnable : std_logic; signal CntBitsOut : std_logic; signal CntTimeOut : std_logic; signal FSMDBus : std_logic_vector(2 downto 0); signal FSMQBus : std_logic_vector(2 downto 0); begin -- LFSR Lfsr : LFSR10 port map ( Clk => Clk, Enable => LfsrEnable, Reset => LfsrReset, Data => LfsrData ); -- comparator Comp : Comparator generic map ( NBits => 10 ) port map ( A => LfsrData, B => std_logic_vector(to_unsigned(Probability, 10)), AGreatThanB => CompOutput ); -- shift register SR : ShiftRegister generic map ( NBits => NLeds ) port map ( Enable => SREnable, Clk => Clk, SerialInput => CompOutput, ParallelOutput => SRData ); -- output latch Lat : Latch generic map ( NBits => NLeds ) port map ( Enable => LatEnable, Clk => Clk, DataIn => SRData, DataOut => Led ); -- two limit counter Cnt : TwoLimitCounter generic map ( NBits => 32, Limit1 => NLeds, Limit2 => NWaitClocks ) port map ( Reset => CntReset, Enable => CntEnable, Clock => Clk, Terminated1 => CntBitsOut, Terminated2 => CntTimeOut ); -- FSM D FFs process (Clk, Reset) begin if (Clk'event and (Clk = '1')) then if (Reset = '1') then FSMQBus <= (others => '0'); else FSMQBus <= FSMDBus; end if; end if; end process; -- FSM next state logic FSMDBus <= "000" when (Reset = '1') else "001" when (FSMQBus = "000") else "010" when (FSMQBus = "001") or (FSMQBus = "011") else "011" when (FSMQBus = "010") and (CntBitsOut = '0') else "100" when (FSMQBus = "010") and (CntBitsOut = '1') else "101" when (FSMQBus = "100") or ((FSMQBus = "101") and (CntTimeOut = '0')) else "001" when (FSMQBus = "101") and (CntTimeOut = '1') else "000"; -- FSM output logic LfsrReset <= '1' when (FSMQBus = "000") else '0'; CntReset <= '1' when (FSMQBus = "001") or (FSMQBus = "100") else '0'; CntEnable <= '1' when (FSMQBus = "010") or (FSMQBus = "101") else '0'; LfsrEnable <= '1' when (FSMQBus = "010") else '0'; SREnable <= '1' when (FSMQBus = "011") else '0'; LatEnable <= '1' when (FSMQBus = "100") else '0'; end Architecture1;
Vídeo con el código VHDL implementado sobre la FPGA Spartan3E de Xilinx.
Todo el codigo puede descargarse de la sección soft. Feliz programación y feliz Navidad :-).
[ añadir comentario ] ( 2737 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 4468 )
( 3 / 4468 )Un receptor serie asíncrono es un módulo de hardware que recibe datos serie de forma asíncrona: es el elemento receptor de una UART. A lo largo de este post se aborda paso a paso el diseño digital y la implementación de un módulo receptor serie asíncrono muy sencillo en VHDL, con un bit de start, un bit de stop y 8 bits de datos, así como su posterior implementación en una FPGA.
Especificaciones del receptor
La idea es crear un módulo muy sencillo que sea capaz de recibir datos en formato 8N1, es decir, 1 bit de start, 8 bits de datos, sin paridad y 1 bit de stop. Se asume el orden de envío estándar LSB --> MSB (primero el bit 0 y por último el bit 7) y una velocidad de 9600 bits por segundo (bps). Además de estas especificaciones "funcionales" se va a intentar que el circuito resultante sea totalmente síncrono (sin gated clocks, que el reloj sea el mismo para todos los sub módulos secuenciales del receptor). Este último requisito facilitará la implementación del módulo sobre cualquier FPGA sin limitación en la cantidad de líneas de reloj y de paso servirá para entender las alternativas al uso de gated clocks en el diseño de circuitos digitales.
Bloques del receptor
Los diferentes bloques que componen el receptor asíncrono son los siguientes:
- Un registro de desplazamiento: donde se irán empujando los bits a medida que lleguen.
- Un latch o registro de salida: donde se realizará una carga paralela desde el registro de desplazamiento del dato recibido una vez se compruebe que la recepción ha sido correcta.
- Dos contadores independientes para realizar la división de frecuencia y el conteo de los bits que van llegando, respectivamente.
- Una máquina de estados (FSM, Finite-State Machine) encargada del control de los contadores, del registro de desplazamiento y del registro de salida.
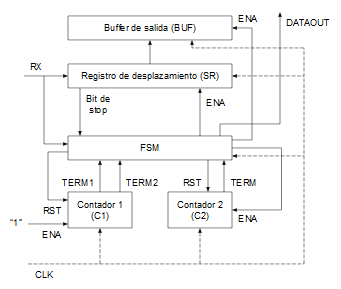
Algoritmo
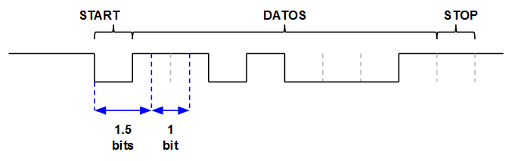
De forma resumida el funcionamiento es el siguiente:
1. En el estado inicial, la FSM espera a que el pin RX valga 0.
2. En el instante en que RX pase a valor 0 la FSM inicializa un contador que tarda el equivalente en tiempo a 1.5 bits a 9600 bps en alcanzar el límite de cuenta, en el momento que este contador alcanza su límite se pasa al siguiente estado.
3. Se inicializa un contador que va a contar la cantidad de bits (8 + 1 bit de stop = 9).
4. Se empuja el valor de RX en el registro de desplazamiento, se reinicia otro contador que tiene como límite el equivalente en tiempo a 1 bit a 9600 bps y se incrementa el contador del número de bits
5. Si el contador de bits vale 9, saltamos al paso 8.
6. Esperamos a que el contador de tiempo para 1 bit llegue al límite
7. Saltamos al paso 4.
8. Si el bit de stop vale 1 cargamos el buffer de salida y hacemos DATAOUT = 1 para indicar que en el buffer de salida hay datos válidos, en caso contrario no se carga de buffer de salida.
9. Saltamos al paso 1.
Evitar el uso de “gated clocks”
En el anterior proyecto en el que se implementó un multiplicador en VHDL usando el algoritmo de Booth, el entorno de desarrollo ISE Design Suite de Xilinx mostraba un warning en el que se indicaba que había que evitar el uso de “gated clocks”.
Un “gated clock” es una línea de reloj que no se corresponde con la salida de un oscilador o un PLL sino que es la salida de una función combinacional o secuencial en un circuito. En el caso del multiplicador implementado en el anterior post, sí se utilizan gated clocks: Por ejemplo, cuando se quiere cargar un registro, la salida del FSM ataca directamente a la entrada de reloj de los biestables de ese registro. Esta forma de trabajar, a priori inocua, tiene varias implicaciones que en aquel proyecto no se tuvieron en cuenta:
1. Como bien me comentó mi colega Armando Sánchez Peña, las líneas de reloj son bienes muy preciados dentro de las FPGAs: su enrutamiento está muy cuidado para garantizar retardos equivalentes independientemente de la parte del chip donde lleguen y debido a ello no podemos disponer de todas las que queramos (aunque tengamos una FPGA con miles de unidades lógicas igual sólo disponemos de unas pocas decenas de líneas de reloj).
2. Los cambios de estado en los biestables de un FSM a veces no son todo lo limpios que uno desearía: Imaginemos que tenemos un FSM con tres estados (“00”, “01” y “11”), para el estado “01” tenemos una lógica de salida que genera un “1” en una entrada de reloj de un registro A y para el estado “11” tenemos una lógica de salida que genera un “1” en una entrada de reloj de otro registro B. Si el FSM está en el estado “00” y tiene que cambiar al estado “11”, es posible que los biestables basculen a velocidades ligeramente diferentes por lo que durante un breve intervalo de tiempo (picosegundos) se podría producir el estado “01” (si el biestable menos significativo es más rápido basculando que el más significativo) ¿Que sucederá durante este picosegundo? Pues que probablemente se produzca una carga espúrea y no deseada del registro A. Estos problemas pueden minimizarse utilizando codificación gray (estados adyacentes se codifican de tal manera que solo cambia de valor un bit) o codificación one-hot (un biestable por estado: gastamos más biestables pero la lógica de salida y de estado siguiente se simplifica por lo que a veces compensa). En posts futuros trataré de profundizará más en estos temas.
En multitud de foros sobre FPGAs y ASICs se comenta lo malo que es el uso de “gated clocks” sin embargo este post y otros ayudan mucho a aclarar este asunto. No todo es blanco o negro:
1. Para FPGAs hay que evitar el uso de gated clocks debido a la cantidad limitada de líneas de reloj de las que disponemos dentro del chip.
2. Para ASICs el uso de gated clocks mientras sea con cabeza (código gray, one-hot, etc.) no sólo es perfectamente válido, sino hasta aconsejable. Hay que tener en cuenta que una señal de reloj es una enorme fuente de consumo de corriente ya que cada vez que bascula la señal de reloj se producen micropicos de corriente debidos a las capacidades presentes en las entradas de reloj de los biestables a los que ataca. Un circuito con gated clocks consumirá menos corriente que su equivalente sin gated clocks.
Como obviamente, salvo casos excepcionales, lo normal es que dispongamos de una FPGA, no de un ASIC, lo lógico es intentar evitar el uso de gated clocks en nuestros diseños digitales. En este caso, como se puede ver en el diagrama de bloques anterior, esa ha sido la consigna que se ha seguido:
1. La misma señal de reloj para todos los módulos.
2. Sustituir los antiguos “gated clocks” por “enables” que permitan habilitar o deshabilitar módulos en un instante dado sin necesidad de enmascarar o tocar la señal de reloj.
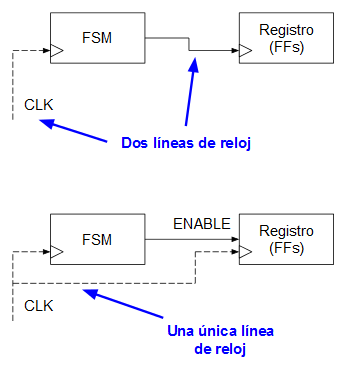
Los enables en circuitos secuenciales se pueden implementar mediante lógica combinacional en los biestables o mediante señales CE (“Chip Enable”) que implementan muchos de los biestables presentes en las FPGAs que hay en el mercado. Para garantizar portabilidad en el código VHDL no se puede presuponer que los biestables de la FPGA vayan a tener entradas CE y dado que en este caso siempre se están usando biestables de tipo D, la opcion más lógica es la indicada en el documento FPGA Design Tips de Xilinx:
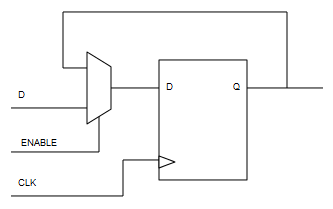
Esta es una forma sencilla de implementar un CE (“Chip Enable”) “a mano”. Cuando el multiplexor selecciona la entrada conectada a la salida Q, el biestable no cambia de estado por muchos ciclos de reloj que le lleguen. Además implementando un CE “a mano” de esta manera, nos aseguramos que el circuito resultante es sintetizable en cualquier FPGA independientemente de si ésta implementa entradas CE en sus biestables o no.
Máquina de estados
La máquina de estados resultante para nuestro módulo de recepción de la UART quedaría, utilizando la técnica de los “enables”, como sigue:
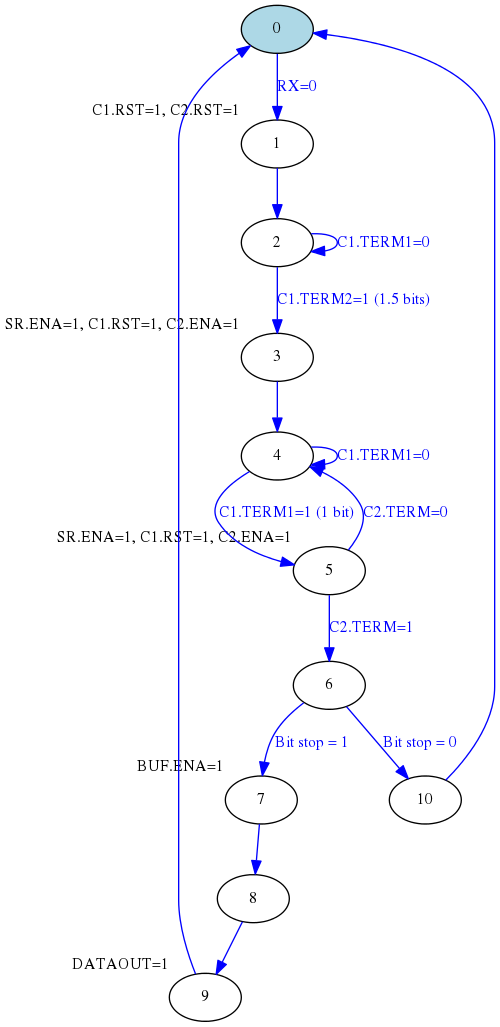
La máquina de estados es una versión “formal” del algoritmo descrito en párrafos anteriores. Como se puede apreciar el contador 1 se utiliza para controlar los tiempos entre los principales cambios de estado (cuando se detecta el bit de start y entre bit y bit de datos).
Contadores
El módulo receptor utiliza dos contadores, uno (contador 1) para contar el tiempo equivalente a 1.5 bits a 9600 bps y el tiempo equivalente a 1 bit a 9600 bps y otro contador (contador 2) para contar los bits que se van empujando en el registro de desplazamiento (9, los 8 de datos más el bit de stop). El segundo contador (contador 2) es trivial ya que cuenta hasta 9 mientras que para el contador 1 sí que es necesario realizar algunos cálculos previos. Consideremos una velocidad de 9600 bps:
$$9600\ \ bits/segundo = {1 \over 9600}\ \ segundos/bit$$
Teniendo en cuenta que, en el caso particular de la placa FPGA Papilio One, el reloj del sistema va a 32MHz tenemos que:
$$(32000000\ \ pulsos/segundo) \times \left({1 \over 9600}\ \ segundos/bit\right) = 3333.33\ \ pulsos/bit$$
Que, redondeando, nos da: 3333 pulsos a 32MHz por bit a 9600 bps. Multiplicando por 1.5 nos dará la cantidad de pulsos a 32MHz necesarios para contar 1.5 bits de tiempo:
$$3333.33 \times 1.5 = 5000\ pulsos\ a\ 32MHz\ por\ 1.5\ bit\ a\ 9600 bps$$
El Contador 1 tendrá, por tanto como límite de cuenta 1 el valor 3333 y como límite de cuenta 2 el valor 5000. En otras palabras, tras un reset en el contador 1, la salida TERM1 de dicho contador 1 se pondrá a “1” cuando pasen 3333 pulsos de reloj del sistema mientras que la salida TERM2 de ese mismo contador 1 se pondrá a “1” cuando pasen 5000 pulsos de reloj del sistema.
VHDL
Ambos contadores (1 y 2) son instancias separadas de un mismo módulo contador (en el caso del contador 2 se ignora la salida TERM2). Al ser tanto el registro de desplazamiento como el registro de salida simplemente arrays de biestables, se ha optado por implementar ambos submódulos dentro de la misma FSM.
library IEEE; use IEEE.std_logic_1164.all; use IEEE.numeric_std.all; entity UartReceiver is port ( Rx : in std_logic; Clock : in std_logic; DataOut : out std_logic_vector(7 downto 0); DataOutOk : out std_logic ); end UartReceiver; architecture Architecture1 of UartReceiver is component TwoLimitCounter is generic ( NBits : integer := 4; Limit1 : integer := 3; Limit2 : integer := 11 ); port ( Reset : in std_logic; Clock : in std_logic; Enable : in std_logic; Terminated1 : out std_logic; Terminated2 : out std_logic ); end component; signal ShiftRegisterDBus : std_logic_vector(8 downto 0); -- 8 bits + 1 bit de stop signal ShiftRegisterQBus : std_logic_vector(8 downto 0); signal ShiftRegisterEnable : std_logic; signal BufferDBus : std_logic_vector(7 downto 0); signal BufferQBus : std_logic_vector(7 downto 0); signal BufferEnable : std_logic; signal Counter1Reset : std_logic; signal Counter1Terminated1 : std_logic; signal Counter1Terminated2 : std_logic; signal Counter2Reset : std_logic; signal Counter2Enable : std_logic; signal Counter2Terminated : std_logic; signal FSMQBus : std_logic_vector(3 downto 0); signal FSMDBus : std_logic_vector(3 downto 0); begin -- registro de desplazamiento process (Clock) begin if (Clock'event and (Clock = '1')) then ShiftRegisterQBus <= ShiftRegisterDBus; end if; end process; -- MSB first (apenas usado) -- ShiftRegisterDBus <= (ShiftRegisterQBus(7 downto 0) & Rx) when (ShiftRegisterEnable = '1') else ShiftRegisterQBus; -- LSB first: los valores se van metiendo por el bit más significativo ShiftRegisterDBus <= (Rx & ShiftRegisterQBus(8 downto 1)) when (ShiftRegisterEnable = '1') else ShiftRegisterQBus; -- buffer de salida process (Clock) begin if (Clock'event and (Clock = '1')) then BufferQBus <= BufferDBus; end if; end process; -- MSB first (apenas usado) -- BufferDBus <= ShiftRegisterQBus(8 downto 1) when (BufferEnable = '1') else BufferQBus; -- LSB first: El bit de stop está en el bit más significativo, el dato en el resto de bits BufferDBus <= ShiftRegisterQBus(7 downto 0) when (BufferEnable = '1') else BufferQBus; -- contador fino para medir 1 y 1,5 bits a 32MHz Counter1: TwoLimitcounter generic map ( NBits => 13, --Limit1 => 50, -- 1 bit a 1MHz --Limit2 => 75 -- 1.5 bits a 1MHz Limit1 => 3333, -- 1 bit a 32MHz Limit2 => 5000 -- 1.5 bits a 32MHz ) port map ( Reset => Counter1Reset, Clock => Clock, Enable => '1', Terminated1 => Counter1Terminated1, Terminated2 => Counter1Terminated2 ); -- contador grueso de bits Counter2: TwoLimitcounter generic map ( NBits => 4, Limit1 => 8, -- poniendo el límite a 8 metemos 9 valores en el registro de desplaz. Limit2 => 0 ) port map ( Reset => Counter2Reset, Clock => Clock, Enable => Counter2Enable, Terminated1 => Counter2Terminated ); -- FSM: Biestables process (Clock) begin if (Clock'event and (Clock = '1')) then FSMQBus <= FSMDBus; end if; end process; -- FSM: Lógica del estado siguiente FSMDBus <= "0001" when (FSMQBus = "0000") and (Rx = '0') else "0010" when (FSMQBus = "0001") or ((FSMQBus = "0010") and (Counter1Terminated2 = '0')) else "0011" when (FSMQBus = "0010") and (Counter1Terminated2 = '1') else "0100" when (FSMQBus = "0011") or ((FSMQBus = "0101") and (Counter2Terminated = '0')) or ((FSMQBus = "0100") and (Counter1Terminated1 = '0')) else "0101" when (FSMQBus = "0100") and (Counter1Terminated1 = '1') else "0110" when (FSMQBus = "0101") and (Counter2Terminated = '1') else "0111" when (FSMQBus = "0110") and (ShiftRegisterQBus(8) = '1') else -- bit de stop ok "1000" when (FSMQBus = "0111") else "1001" when (FSMQBus = "1000") else "1010" when (FSMQBus = "0110") and (ShiftRegisterQBus(8) = '0') else -- bit de stop mal "0000"; -- FSM: Lógica de salida ShiftRegisterEnable <= '1' when (FSMQBus = "0011") or (FSMQBus = "0101") else '0'; BufferEnable <= '1' when (FSMQBus = "0111") else '0'; Counter1Reset <= '1' when (FSMQBus = "0001") or (FSMQBus = "0011") or (FSMQBus = "0101") else '0'; Counter2Reset <= '1' when (FSMQBus = "0001") else '0'; Counter2Enable <= '1' when (FSMQBus = "0011") or (FSMQBus = "0101") else '0'; DataOutOk <= '1' when (FSMQBus = "1001") else '0'; -- salida paralelo DataOut <= BufferQBus; end Architecture1;
Se trata de un diseño RTL, por lo que la implementación en VHDL es trivial, directa y siempre sintetizable.
A continuación puede verse una simulación en la que se recibe el valor serie 0x53:

La señal COUNTER1TERMINATED2 indica que han pasado 1.5 bits de datos desde el reset del contador 1 mientras que la señal COUNTER1TERMINATED1 indica que ha pasado 1 bit de datos desde el reset del contador 1.
Implementación física
A la placa Papilio One (Xilinx Spartan3E) se le conectó por un lado un array de 8 leds (conectado internamente al registro de salida del módulo receptor de la UART) y, por otro lado un módulo USBSerial basado en el chip FT232R, dicho módulo permite mediante un jumper seleccionar una operación a 3.3V (la FPGA incluida en la placa Papilio One no es tolerante a 5V): Se conectó la salida TX del módulo a un pin de la FPGA conectado internamente a la señal RX del módulo receptor.
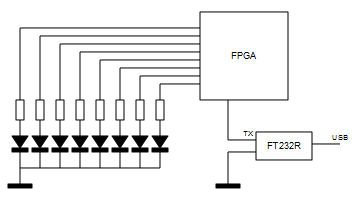

En la foto se puede ver al receptor cargando un carácter 'i' (hexadecimal 69) enviado por el puerto serie desde el ordenador.
Todo el código fuente puede descargarse de la sección soft.
[ añadir comentario ] ( 2472 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 4402 )
( 3 / 4402 )El algoritmo de multiplicación de Booth permite multiplicar enteros con signo en complemento a dos utilizando una técnica muy sencilla basada en desplazamientos y sumas. A lo largo de este post se abordará el diseño y la codificación en VHDL de dicho algoritmo así como su implementación final en una FPGA.
El algoritmo
En la Wikipedia hay una explicación muy clara y detallada del algoritmo de Booth (https://es.wikipedia.org/wiki/Algoritmo_de_Booth). En este caso se ha asumido, por simplicidad, que ambos términos (multiplicando y multiplicador) tienen la misma cantidad de bits.
Partimos de dos números enteros X e Y, ambos de N bits:
1. Construimos una matriz de 3 filas y N+N+1 columnas. La primera fila la llamaremos A, la segunda S y la tercera P.
1.1. En los N bits más significativos de A metemos X, el resto de bits de A los ponemos a 0.
1.2. En los N bits más significativos de S metemos -X (complemento a 2 de X), el resto de bits de S los ponemos a 0.
1.3. En los N bits más significativos de P metemos 0s, a continuación metemos los N bits de Y y en el bit que queda (el menos significativo) metemos un 0.
2. Hacer N veces:
2.1. Si los dos bits menos significativos de P son 01, hacer P <- P + A, en caso de que sean 10, hacer P <- P + S, en caso de que sean 00 o 11, no hacer nada
2.2. Hacer un desplazamiento aritmético (incluyendo el signo) de P hacia la derecha.
3. El resultado de la multiplicación serán los bits N a 1 de P (ojo, el bit 0 de P no forma parte de la solución).
Se trata de un algoritmo muy sencillo y que debe ser implementado de forma secuencial.
El flujo de datos
A continuación puede verse de forma esquemática cómo sería el flujo de datos en el multiplicador.
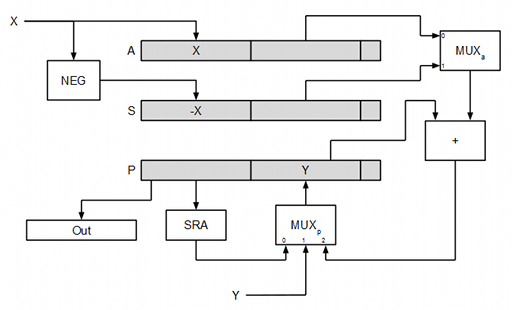
El multiplexor MUXa permite seleccionar entre la operación “P + A” o “P + S”, mientras que el multiplexor MUXp permite seleccionar entre al desplazamiento aritmético hacia la derecha de P, la entrada (para cargar el valor inicial de P a partir del operando Y) y la salida del sumador.
La unidad de control del multiplicador
Para gobernar las señales de carga de los registros y las señales de selección de los multiplexores es necesario implementar una unidad de control. La unidad de control se implementará mediante una máquina de estados finita (FSM) formada por biestables D, lógica de estado siguiente y lógica de salida de tipo Moore.
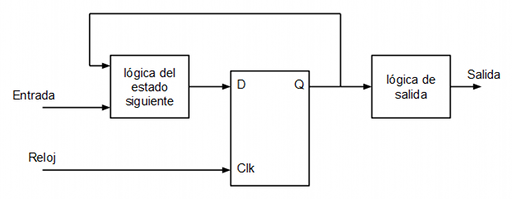
En este caso la máquina de estados que implementaría el algoritmo de Booth sería la siguiente:
Supongamos que se quiere multiplicar -3 por 2 utilizando una mantisa de 5 bits. En este caso:
-3 dec = 11101 bin
2 dec = 00010 bin
- Estado 0.
- Estado 1: MUXp=Y, Resetear el contador.
- Estado 2: Cargar A, Cargar S, Cargar P (se carga Y), Avanzar el contador.
- Estado 3.
Estando en el estado 3 los dos bits menos significativos de P valen en este momento “00” (P1=P0)y el contador no ha terminado (Ct=0), por lo que se va a estado 8.
- Estado 8: MUXp = SRA(P) (desplazamiento aritmético a la derecha de P un bit).
- Estado 9: MUXp = SRA(P), Cargar P (P <- SRA(P)).
- Estado 10: Avanzar el contador.
- Estado 3.
Estando en el estado 3 los dos bits menos significativos de P valen en este momento “10” (P1=1 y P0=0) y el contador no ha terminado (Ct=0), por lo que se va de nuevo al estado 6.
- Estado 6: MUXp = Sumador, MUXa = A.
- Estado 7: MUXp = Sumador, MUXa = A, Cargar P (P <- P + A)
- ...
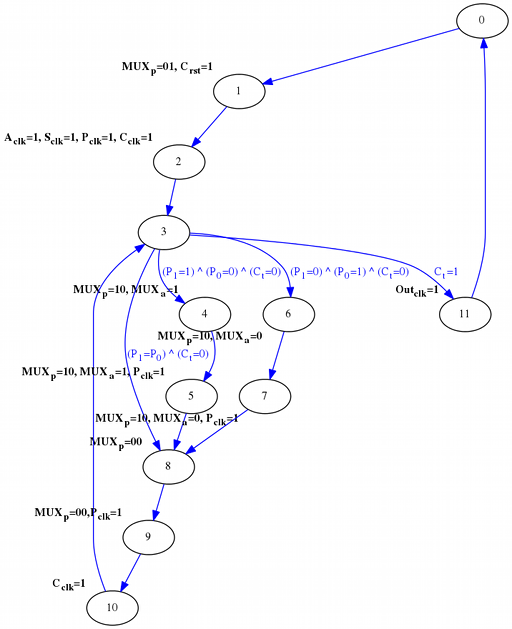
Y así sucesivamente. Como se puede ver en el grafo de la FSM la multiplicación termina cuando, estando en el estado 3, el contador llega al final:
- ...
- Estado 3: Si el contador ha terminado pasamos al estado 11.
- Estado 11: Cargar Out (Out <- P).
- Estado 0 (se vuelve a empezar).
- ...
El el siguiente diagrama puede verse cómo quedaría todo el conjunto (registros, multiplexores, sumador y unidad de control) con lo que serían las entradas y salidas finales del multiplicador.
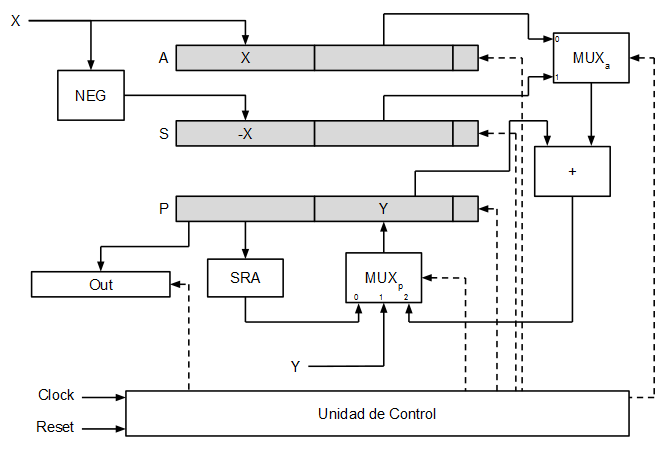
Implementación en VHDL
Para implementar en VHDL el FSM de la unidad de control basta con traducir el FSM a un modelo RTL: se traducen los arcos del grafo a lógica de estado siguiente y las salidas indicadas en los nodos del grafo a lógica de salida.
library ieee; use ieee.std_logic_1164.all; entity MultiplierControlUnit is generic ( NBits : integer := 4 ); port ( Clock : in std_logic; Reset : in std_logic; P1 : in std_logic; P0 : in std_logic; LoadA : out std_logic; LoadS : out std_logic; LoadP : out std_logic; LoadOut : out std_logic; AdderMuxSel : out std_logic; PMuxSel : out std_logic_vector(1 downto 0) ); end MultiplierControlUnit; architecture Architecture1 of MultiplierControlUnit is component Counter generic ( NBits : integer := 4; Limit : integer := 3 ); port ( Reset : in std_logic; Clock : in std_logic; Terminated : out std_logic ); end component; signal DBus : std_logic_vector(3 downto 0); signal QBus : std_logic_vector(3 downto 0); signal CounterReset : std_logic; signal CounterClock : std_logic; signal CounterTerminated : std_logic; begin -- counter for shift loop C : Counter generic map ( NBits => 8, Limit => NBits ) port map ( Reset => CounterReset, Clock => CounterClock, Terminated => CounterTerminated ); -- D flip-flop with synchronous reset for FSM process (Clock, Reset) begin if (Clock'event and (Clock = '1')) then if (Reset = '1') then QBus <= (others => '0'); else QBus <= DBus; end if; end if; end process; -- next state logic DBus <= "0001" when (QBus = "0000") else "0010" when (QBus = "0001") else "0011" when ((QBus = "0010") or (QBus = "1010")) else "0100" when ((QBus = "0011") and (P1 = '1') and (P0 = '0') and (CounterTerminated = '0')) else "0101" when (QBus = "0100") else "0110" when ((QBus = "0011") and (P1 = '0') and (P0 = '1') and (CounterTerminated = '0')) else "0111" when (QBus = "0110") else "1000" when ((QBus = "0101") or (QBus = "0111") or ((QBus = "0011") and (P1 = P0) and (CounterTerminated = '0'))) else "1001" when (QBus = "1000") else "1010" when (QBus = "1001") else "1011" when ((QBus = "0011") and (CounterTerminated = '1')) else "0000"; -- output logic LoadA <= '1' when (QBus = "0010") else '0'; LoadS <= '1' when (QBus = "0010") else '0'; LoadP <= '1' when ((QBus = "0010") or (QBus = "0101") or (QBus = "0111") or (QBus = "1001")) else '0'; LoadOut <= '1' when (QBus = "1011") else '0'; PMuxSel <= "01" when ((QBus = "0001") or (QBus = "0010")) else -- Y "10" when ((QBus = "0100") or (QBus = "0101") or (QBus = "0110") or (QBus = "0111")) else -- + "00" when ((QBus = "1000") or (QBus = "1001")) else "11"; AdderMuxSel <= '0' when ((QBus = "0110") or (QBus = "0111")) else -- A '1' when ((QBus = "0100") or (QBus = "0101")) else -- S '0'; CounterReset <= '1' when ((QBus = "0001") or (QBus = "0010")) else '0'; CounterClock <= '1' when ((QBus = "0010") or (QBus = "1010")) else '0'; end Architecture1;
La unidad de control incluye un contador interno (el componente instanciado como C) encargado de controlar la cantidad de veces que itera el bucle del algoritmo. En el caso del algoritmo de Booth el bucle itera tantas veces como bits tiene la mantisa (al instanciar el contador C hacemos Limit => NBits).
Como puede apreciarse, se trata de un diseño totalmente basado en modelos RTL (https://en.wikipedia.org/wiki/Register-transfer_level) por lo que su implementación es relativamente sencilla y el código generado siempre es sintetizable.
Todo el código fuente se puede descargar de la sección soft.
[ añadir comentario ] ( 2568 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 4682 )
( 3 / 4682 )Aprovechando el post anterior en el que se usaba el DAC de la placa Teensy 3.1 para generar un bucle sonido, he ido un poco más allá y he implementado un pequeño sintetizador monofónico de modelado analógico. La secuenciación es por ahora interna (en una siguiente iteración, se le incorporará una entrada MIDI) e incluye un oscilador de onda en diente de sierra o cuadrada, un filtro de estado variable configurable como paso bajo, paso banda, paso alto y elimina-banda, una envolvente para la frecuencia de corte del filtro y una envolvente para la amplitud.
Punto de partida
En este post anterior se diseñó e implementó un reproductor de sonido para el Teensy que almacenaba un bucle en la memoria flash del microcontrolador. Se utilizó el DAC de 12 bits que viene de serie con el microcontrolador MK20 del Teensy y para el envío de muestras a dicho DAC se usó la interrupción periódica Systick, que traen de serie todos los microcontroladores ARM Cortex-M, ajustada a la frecuencia de muestreo.
void systick() __attribute__ ((section(".systick"))); void systick() { DACDAT = next sample } int main() { // configure DAC SIM_SCGC2 |= (1 << 12); // enable DAC clock generator DAC0_C1 = 0x00; // disable DAC DMA DAC0_C0 = 0xC0; // enable DAC for VREF2 (3.3v) // configure SYSTICK SYST_RVR = F_CPU / SAMPLE_RATE; SYST_CVR = 0; SYST_CSR |= 0x07; while (1) ; }
Objetivo
El objetivo planteado en este caso era implementar un pequeño sintetizador monofónico partiendo de ese mismo modelo (interrupción Systick + DAC). Los bloques planteados para el mini sintetizador son los siguientes:
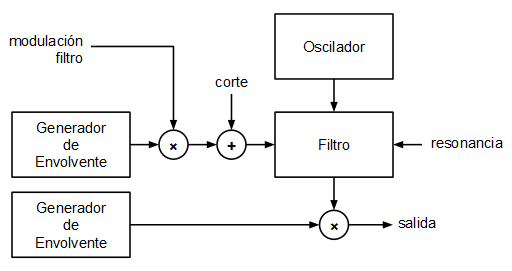
El oscilador
Se ha planteado un oscilador muy sencillo basado en tabla de ondas. Un oscilador basado en tabla de ondas consiste en uno o varios arrays con los valores de la onda que queremos generar, en cada array se guarda un único ciclo de onda y el oscilador lo que hace para emitir tonos a diferente frecuencia es recorrer dicha tabla a diferentes velocidades dando la vuelta cuando llega al final:
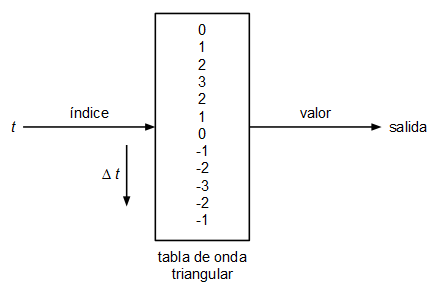
El tamaño de la tabla de ondas vendrá determinado por la resolución (calidad) que queramos darle y por la frecuencia de muestreo. Imaginemos que tenemos un array con 100 valores de una onda con forma de diente de sierra:
// 100 enteros con signo entre -50 y 49
[-50, -49, -48, -47, ... , 47, 48, 49]
Si la frecuencia de muestreo es de 44100 Hz (la frecuencia de muestreo estándar de calidad CD) y queremos reproducir un tono de 440 Hz (nota LA de la cuarta octava del piano) a partir de esta tabla de ondas el oscilador tendrá que usar un incremento de:
$$\Delta t = {440 \over {44100 \over 100}} = 0.9977324263$$
Esto es, el oscilador tomará la primera muestra de la posición 0 de la tabla, la siguiente muestra la tomará de la posición 0.9977324263, la siguiente de la posición 1.9954648526, y así sucesivamente. Como obviamente se trata de una tabla con posiciones enteras, en cada iteración se coge la muestra más próxima o se interpola.
En este caso se ha optado por usar la muestra en la posición de la parte entera del índice. No es la mejor forma de hacerlo pero sí la más rápida:
| t | índice (parte entera de t) |
|---|---|
| 0 | 0 |
| 0.9977324263 | 0 |
| 1.9954648526 | 1 |
| 2.9931972789 | 2 |
| 3.9909297052 | 3 |
| ... | |
| 99.77324263 | 99 |
| 100.7709750563 | |
| como la tabla mide 100, en este momento se vuelve a empezar, manteniendo la parte fraccionaria | |
| 0.7709750563 | 0 |
| 1.7687074826 | 1 |
| 2.7664399089 | 2 |
| ... | |
Debido a que estamos haciendo la implementación en un procesador sin unidad de coma flotante, se realizan todos los cálculos usando aritmética de punto fijo. El formato elegido es el Q16.16 (16 bits enteros + 16 bits fraccionarios = 32 bits que pueden alojarse en un tipo int32_t). Se definen, además, varias macros para facilitar la comprensión del código:
typedef int32_t fixedpoint_t; #define __FP_INTEGER_BITS 16 #define __FP_FRACTIONAL_BITS 16 #define __TO_FP(a) (((int32_t) (a)) << __FP_FRACTIONAL_BITS) #define __FP_1 (((int32_t) 1) << __FP_FRACTIONAL_BITS) #define __FP_ADD(a, b) (((int32_t) (a)) + ((int32_t) (b))) #define __FP_SUB(a, b) (((int32_t) (a)) - ((int32_t) (b))) #define __FP_MUL(a, b) ((int32_t) ((((int64_t) (a)) * ((int64_t) (b))) >> __FP_FRACTIONAL_BITS)) #define __FP_DIV(a, b) ((int32_t) ((((int64_t) (a)) << __FP_FRACTIONAL_BITS) / ((int64_t) (b))))
El código del método getNextSample del oscilador (el que se invoca para calcular cada muestra) queda, por tanto, como sigue:
fixedpoint_t Oscillator::getNextSample() { if (this->status == STATUS_STOPPED) return 0; else if (this->status == STATUS_STARTED) { fixedpoint_t v = ((fixedpoint_t) Wavetable::VALUES[this->t >> __FP_FRACTIONAL_BITS]); if (this->patch->waveform == OscillatorPatch::WAVEFORM_SQUARE) v = (v > 0) ? __TO_FP(1) : __TO_FP(-1); this->t = __FP_ADD(this->t, this->inc); if (this->t >= Wavetable::SIZE_FP) this->t = __FP_SUB(this->t, Wavetable::SIZE_FP); return v; } else return 0; }
Como se puede ver, el atributo t del objeto es el que se va incrementando y a la hora de determinar qué valor devuelve el método getNextSample() se usa como índice de la tabla simplemente la parte entera de t. Esta decisión no es gratuita e implica que hay que tratar de que los incrementos siempre sean mayores o iguales a 1 para que no se produzcan "escalones" en la señal de salida debido a que se repitan muestras de la tabla: en el ejemplo anterior la primera muestra (t = 0) y la segunda (t = 0.9977324263) serán la misma ya que la parte entera de ambos valores es 0. Para evitar que se produzcan estos escalones se ha optado por incrementar el tamaño de la tabla de ondas.
Si partimos de la base de que la frecuencia del tono es directamente proporcional al incremento de t, se puede buscar un tamaño de tabla tal que, para la frecuencia más baja que se quiera reproducir, se obtenga un incremento de t igual a 1. En efecto, si consideramos que no vamos a reproducir tonos por debajo de los 20 Hz (límite inferior del umbral de audición humano), definiendo las tablas de ondas con un tamaño de
$${44100 \over 20} = 2205 \thinspace muestras$$
Para cualquier tono que queramos reproducir, tendremos siempre un incremento de t mayor o igual a 1. Por otro lado podemos simplificar la ecuación del cálculo del incremento de t:
$$\Delta t = {f_{tono} \over 20}$$
Debido a que el propio cálculo del incremento de t implica una división y las divisiones consumen gran cantidad de recursos en procesadores sin unidad de división (como es el caso del ARM Cortex-M) se ha optado por meter en una tabla los diferentes valores del incremento de t. El índice de dicha tabla es el índice de la nota MIDI (entre 0 y 127).
const fixedpoint_t Wavetable::MIDI_FREQ_INC[128] = { 0, 28384, 30071, 31859, 33754, 35761, 37887, 40140, 42527, 45056 ... 34563955, 36619234, 38796727, 41103701 };
Con esta tabla precalculada sintonizar el oscilador solo requiere una indexación y una asignación:
void Oscillator::noteOn(uint8_t midiKey, uint8_t midiVelocity) { this->inc = Wavetable::MIDI_FREQ_INC[midiKey]; this->status = STATUS_STARTED; }
Generador de envolvente
Se utilizan dos generadores de envolvente independientes. Uno que modula la frecuencia de corte del filtro y otro que modula la amplitud del sonido final, antes de escribirlo en el DAC. El tipo de envolvente más común y el que se ha utilizado en este caso es el tipo ADSR (Attack-Decay-Sustain-Release). Cada envolvente de este tipo posee tres valores característicos: el tiempo de ataque (A), el tiempo de caída (D), el nivel de sostenido (S) y el tiempo de liberación (R). Se puede ver un generador de envolvente como una generador de una señal muy lenta que varía entre 0 y 1.
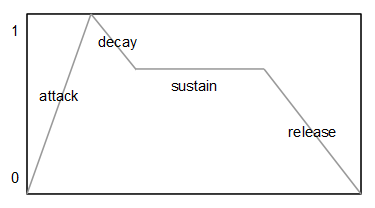
Si se define un nivel de sostenido igual a 0, tenemos una envolvente de tipo AD (Attack-Decay).
Aunque lo más común es definir los parámetro A, D y R en unidades de tiempo (milisegundos, microsegundos), en este caso se ha optado por indicar dichos valores en forma de incrementos, de esta forma no es necesario realizar ninguna multiplicación ni división por cada muestra que se calcula.
fixedpoint_t EnvelopeGenerator::getNextSample() { uint8_t localStatus = this->status; fixedpoint_t ret = 0; do { this->status = localStatus; if (localStatus == STATUS_STOP) ret = 0; else if (localStatus == STATUS_ATTACK) { ret = this->lastSample + this->patch->attackInc; if (ret >= __TO_FP(1)) { ret = __TO_FP(1); localStatus = STATUS_DECAY; } } else if (localStatus == STATUS_DECAY) { ret = this->lastSample - this->patch->decayInc; if (ret <= this->patch->sustainLevel) { ret = this->patch->sustainLevel; if (ret == 0) localStatus = STATUS_STOP; else localStatus = STATUS_SUSTAIN; } } else if (localStatus == STATUS_SUSTAIN) { ret = this->patch->sustainLevel; if (this->noteOffReceived) { this->noteOffReceived = false; localStatus = STATUS_RELEASE; } } else if (localStatus == STATUS_RELEASE) { ret = this->lastSample - this->patch->releaseInc; if (ret <= 0) { ret = 0; localStatus = STATUS_STOP; } } } while (localStatus != this->status); this->lastSample = ret; return __FP_MUL(ret, this->amplitude); }
En la fase de ataque (A) se va incrementando la señal de salida desde 0 hasta 1 en pasos attackInc, en la fase de caída (D) se va decrementando la señal de salida desde 1 hasta el nivel de sostenido en pasos decayInc. Si el nivel de sostenido es 0 la envolvente para al terminar la fase de caída (D), en caso contrario mantiene el nivel de sostenido hasta que se invoca el método noteOff. En ese momento se inicia la fase de liberación (R) decrementando la señal de salida desde el nivel de sostenido hasta 0 en pasos releaseInc.
Filtro
A la hora de implementar un filtro digital existen diferentes aproximaciones: discretización de filtros analógicos conocidos, diseño digital directo usando diagrama de polos y ceros, etc. En este caso se ha optado por una conocida implementación publicada en el libro “Musical Applications of Microprocessors” de Hal Chamberlin. Se trata de una implementación en digital de un filtro de estado variable que permite extraer señales paso bajo, paso banda, paso alto y elimina banda utilizando muy pocos cálculos.
Dicho filtro viene caracterizado por el siguiente sistema de ecuaciones en diferencias:
$$pasoAlto[n] = entrada - ({r \times pasoBanda[n-1]}) - pasoBajo[n]$$
$$pasoBanda[n] = ({f \times pasoAlto[n]}) + pasoBanda[n - 1]$$
$$pasoBajo[n] = ({f \times pasoBanda[n - 1]}) + pasoBajo[n - 1]$$
Siendo:
$$f = 2\sin\left({\pi F_c \over F_s}\right)$$
$$r = {1 \over Q}$$
Siendo $F_c$ la frecuencia de corte del filtro, $F_s$ la frecuencia de muestreo y $Q$ la Q del filtro (la resonancia).
Si se reordenan las ecuaciones en diferencias:
$$pasoBajo[n] = ({f \times pasoBanda[n - 1]}) + pasoBajo[n - 1]$$
$$pasoAlto[n] = entrada - ({r \times pasoBanda[n - 1]}) - pasoBajo[n]$$
$$pasoBanda[n] = ({f \times pasoAlto[n]}) + pasoBanda[n - 1]$$
Podemos olvidarnos de los índices:
pasoBajo += f * pasoBanda
pasoAlto = entrada - (r * pasoBanda) - pasoBajo
pasoBanda += f * pasoAlto
Como se puede apreciar es preciso mantener en memoria al menos las variables “pasoBajo” y “pasoBanda” entre que se procesa una muestra y la siguiente (se trata de un filtro digital de segundo orden).
fixedpoint_t StateVariableFilter::getNextSample(fixedpoint_t input) { this->lowPass = __FP_ADD(this->lowPass, __FP_MUL(this->cutoff, this->bandPass)); fixedpoint_t highPass = __FP_SUB(__FP_SUB(input, this->lowPass), __FP_MUL(this->resonance, this->bandPass)); this->bandPass = __FP_ADD(this->bandPass, __FP_MUL(this->cutoff, highPass)); if (this->mode == MODE_LOWPASS) return this->lowPass; else if (this->mode == MODE_BANDPASS) return this->bandPass; else if (this->mode == MODE_HIGHPASS) return highPass; else if (this->mode == MODE_NOTCH) return __FP_ADD(highPass, this->lowPass); return 0; }
Voz
En la clase Voice juntamos los elementos que se han definido hasta ahora. Esta clase implementa también la interface Generator:
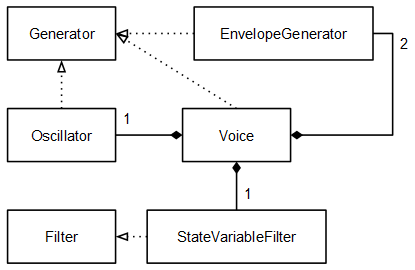
void Voice::noteOn(uint8_t midiKey, uint8_t midiVelocity) { this->oscillator.noteOn(midiKey, midiVelocity); this->ampEnv.noteOn(midiKey, midiVelocity); this->filterEnv.noteOn(midiKey, midiVelocity); } void Voice::noteOff(uint8_t midiKey) { this->oscillator.noteOff(midiKey); this->ampEnv.noteOff(midiKey); this->filterEnv.noteOff(midiKey); } fixedpoint_t Voice::getNextSample() { fixedpoint_t o = this->oscillator.getNextSample(); fixedpoint_t env = __FP_MUL(this->filterEnv.getNextSample(), this->filterEnvMod); fixedpoint_t cutoff = __FP_ADD(env, this->cutoff); if (cutoff < 0) cutoff = 0; else if (cutoff > __TO_FP(1)) cutoff = __TO_FP(1); this->filter.cutoff = cutoff; fixedpoint_t aux = this->filter.getNextSample(o); fixedpoint_t e = this->ampEnv.getNextSample(); return __FP_MUL(aux, e); }
Ahora cada objeto Voice es un sintetizador monofónico. Si en un futuro se quisiese implementar un sintetizador polifónico simplemente habría que instanciar tantos objetos Voice como voces de polifonía se quisieran.
Secuenciador
Aunque en el diagrama inicial no aparece, es fundamental implementar un secuenciador si se quiere probar el sintetizador y no podemos o no queremos pelearnos aún con la implementación de una entrada MIDI. El secuenciador se encarga de disparar notas en determinados instantes de tiempo, en otras palabras, es el objeto que “toca” el instrumento.
En este caso se ha optado por la implementación de un sencillo secuenciador de 16 pasos equidistantes en semicorcheas. 16 semicorcheas forman un compás de 4 por 4 por lo que toca un único compás. El secuenciador vuelve al empezar cuando llega al final: después de tocar la nota de la semicorchea 15, empieza de nuevo en la semicorchea 0.
void Sequencer::setBPM(uint16_t bpm) { uint32_t stepsPerMinute = bpm * 4; // semicorcheas (pasos de secuenciador) por minuto this->n = (Generator::SAMPLES_MS * ((uint32_t) 60000)) / stepsPerMinute; // muestras por semicorchea }
Como el método run se invoca cada vez que se va a generar una muestra (SAMPLE_RATE veces por segundo) se disparará una nota cada vez que un contador interno llegue a n.
void Sequencer::run() { if (this->status == STATUS_PLAY) { if (this->t == 0) { uint8_t note = this->midiNote[this->nextNoteIndex]; if ((note > 0) && (this->generator != NULL)) this->generator->noteOn(note, 100); this->nextNoteIndex++; if (this->nextNoteIndex == SEQUENCE_SIZE) this->nextNoteIndex = 0; } this->t++; if (this->t == this->n) this->t = 0; } }
Nótese que el secuenciador no envía eventos de tipo “noteOff”. Esto está hecho así adrede para este caso concreto por simplicidad, y porque las envolventes que se usan tienen siempre el nivel de sostenido a 0 (el sonido se acaba extinguiendo aunque el secuenciador no envíe eventos “noteOff”). Como la clase Voice implementa la interface Generator, le podemos decir al secuenciador que mande los disparos de nota (“noteOn”) al objeto de tipo Voice:
Voice v;
Sequencer seq;
...
seq.setBPM(120);
seq.setGenerator(v);
De esta forma ya tenemos adecuadamente inicializado el secuenciador. Ahora sólo falta meter las notas MIDI que queramos que toque. Un valor de nota igual a 0 indica al secuenciador que no queremos disparar ninguna nota en esa semicorchea:
seq.midiNote[0] = 36; // Do 1 seq.midiNote[1] = 24; // Do 0 seq.midiNote[2] = 0; seq.midiNote[3] = 36; // Do 1 seq.midiNote[4] = 39; // Re# 1 seq.midiNote[5] = 0; seq.midiNote[6] = 0; seq.midiNote[7] = 39; // Re# 1 seq.midiNote[8] = 36; // Do 1 seq.midiNote[9] = 24; // Do 0 seq.midiNote[10] = 0; seq.midiNote[11] = 36; // Do 1 seq.midiNote[12] = 39; // Re# 1 seq.midiNote[13] = 0; seq.midiNote[14] = 0; seq.midiNote[15] = 43; // Sol 1 seq.start(); // cambiamos el estado interno del secuenciador a STATUS_PLAY
En este caso se ha metido una sencilla secuencia típica de música electrónica, en la escala de Do menor.
Juntándolo todo
El secuenciador invoca al método “noteOn” del objeto Voice cada vez que hay una nota nueva que tocar y el valor devuelto por el método “getNextSample” del objeto de tipo Voice es el que se manda al DAC. La señal debe ser adaptada de fixedpoint_t a entero sin signo de 12 bits (0 - 4095):
void systick() { seq.run(); fixedpoint_t aux = v.getNextSample() >> 1; // evitar clipping uint16_t out; if (aux >= __TO_FP(1)) out = 4095; else if (aux <= __TO_FP(-1)) out = 0; else out = (uint16_t) (((aux + 32768) >> 4) & 0x00000FFF); DACDAT = out; }
Resultados
En la implementación final realizada se ha optado por utilizar una frecuencia de muestreo de 32 KHz. Usar esta frecuencia de muestreo permite generar tonos más precisos ya que 96 MHz no es divisible entre 44.1 KHz pero sí lo es entre 32 KHz (la frecuencia de muestreo es más precisa a 32 KHz que a 44.1 KHz).
A continuación un vídeo en el que puede verse y oirse el invento. No se oye muy alto porque tuve que poner el volumen bajo (era tarde cuando grabé) y encima pasó un camión en ese momento por la calle ¬¬
Todo el código fuente está disponible en la sección soft.
[ añadir comentario ] ( 2759 visualizaciones ) | [ 0 trackbacks ] | enlace permanente | enlace relacionado |




 ( 3 / 4170 )
( 3 / 4170 )
 Calendario
Calendario




