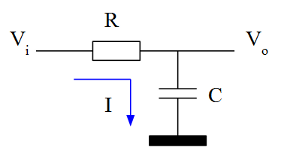
El circuito
Partimos de un circuito estándar RC. En el que R, C y $V_i$ son constantes. El objetivo es calcular la curva de la salida $V_o$ con respecto al tiempo:
La ecuación
Si asumimos que a través de la salida no se consume corriente, la corriente que circula por la resistencia:
$$I={V_i - V_o \over R}$$
Será igual a la corriente que circula por el condensador:
$$I=C{dV_o \over dt}$$
Igualando ambas expresiones obtenemos la ecuación básica de este circuito:
$${V_i - V_o \over R}=C{dV_o \over dt} \Rightarrow {V_i \over RC} - {V_o \over RC}={dV_o \over dt}$$
Solución analítica
Se trata de una ecuación diferencial lineal de primer orden:
$$y^\prime+p(x)y=q(x)$$
$$ y(x_0)=y_0 $$
Ya que si cambiamos el orden de los operandos:
$${dV_o \over dt}+{1 \over RC}V_o={V_i \over RC}$$
Se ve fácilmente que:
$$y=V_o$$
$$x=t$$
$$p(x)={1 \over RC}$$
$$q(x)={V_i \over RC}$$
Por tanto se puede calcular en valor de $V_o$ en función de $t$ usando la forma estándar de resolución de este tipo de ecuaciones diferenciales:
$$V_o=e^{-\int_{0}^{t}p(s)ds}\left[ V_o(0)+\int_{0}^{t}q(s)e^{\int_{0}^{s}p(v)dv}ds\right]$$
Siendo $V_o(0)$ el valor de $V_o$ en el instance inicial (0 si el condensador está totalmente descargado). Como tenemos que:
$$\int_{0}^{w}p(t)dt=\int_{0}^{w}{1 \over RC}dt={1 \over RC}\int_{0}^{w}dt={1 \over RC}\left[t\right]_{0}^{w}={w \over RC}$$
Entonces podemos reescribir la ecuación de $V_o$ como:
$$V_o=e^{-{t \over RC}}\left[V_o(0)+\int_{0}^{t}{V_i \over RC}e^{s \over RC}ds\right]$$
Calculando la integral de dentro tenemos que:
$$\int_{0}^{t}{V_i \over RC}e^{s \over RC}ds={V_i \over RC}\int_{0}^{t}e^{s \over RC}ds={V_i \over RC}\left[RCe^{s \over RC}\right]_{0}^{t}={V_i \over RC}\left(RCe^{t \over RC}-RCe^0\right)=V_i\left(e^{t \over RC}-1\right)$$
Sustituyendo ahora la integral por su resultado, la ecuación $V_o$ la podemos reescribir de la siguiente manera:
$$V_o=e^{-{t \over RC}}\left(V_o(0)+V_i\left(e^{t \over RC}-1\right)\right)=e^{-{t \over RC}}V_o(0)+e^{-{t \over RC}}V_i\left(e^{t \over RC}-1\right)$$
$$V_o=e^{-{t \over RC}}V_o(0)+V_i\left(e^{-{t \over RC}}e^{t \over RC}-e^{-{t \over RC}}\right)=e^{-{t \over RC}}V_o(0)+V_i\left(1-e^{-{t \over RC}}\right)$$
Con lo que nos sale:
$$V_o=e^{-{t \over RC}}V_o(0)+V_i\left(1-e^{-{t \over RC}}\right)$$
Nótese que si despejamos la $t$ se puede saber el tiempo que tarda el condensador en alcanzar un voltaje final $V_o$ partiendo de un voltaje de salida inicial $V_o(0)$ y con un voltaje de entrada de $V_i$:
$$t=-RC\log\left({V_o-V_i \over V_o(0)-V_i}\right)$$
Solución numérica
Para obtener una solución numérica lo que hacemos en este caso es despejar la derivada de la salida en la ecuación inicial:
$${dV_o \over dt}={V_i \over RC}-{V_o \over RC}={V_i-V_o \over RC}$$
Por lo tanto la salida $V_o$ en el instante $t=s$ será:
$$V_o=\int_{0}^{s}{V_i-V_o \over RC}dt$$
Esta integral definida podemos aproximarla mediante un método de integración numérica. En este caso, por simplicidad, optaremos por uno de los métodos de integración numérica más sencillos: el método de Euler. Según este método, si tenemos que:
$${dy \over dx}=f(x,y)$$
Entonces $y$ lo podemos aproximar mediante la siguiente ecuación de recurrencia:
$$y_n=y_{n-1}+h \times f(x_{n-1},y_{n-1})$$
Siendo $h$ un valor que tiende a cero. En el caso que nos ocupa:
$$y=V_o$$
$$x=t$$
$$f(t,V_o)={V_i-V_o \over RC}$$
Por lo tanto la ecuación de recurrencia del método de Euler quedaría como sigue:
$$V_{o_n}=V_{o_{n-1}}+h \times {V_i-V_{o_{n-1}} \over RC}$$
Las condiciones iniciales vendrán determinadas, al igual que la solución analítica por el valor de $V_o$ cuando $n=0$.
Representación de ambas soluciones
A continuación puede verse un código en lenguaje Octave (software libre de cálculo numérico) que pinta superpuestas las gráficas resultantes de ambas soluciones asumiento con condiciones iniciales nulas ($V_o=0$, i.e. condensador totalmente descargado, en el instante inicial).
global R = 10000; % R = 10 K global C = 0.000001; % C = 1 uF global Vi = 3.3; % Vi = 3.3 voltios global h = 0.001; global t = [0:h:0.1]; % entre 0 y 0.1 segundos con pasos de h = 0.001 segundos % solución analítica con condiciones iniciales nulas Vo_analytic = Vi * (1 - exp(-t ./ (R * C))); % solución numérica function ret = f(Vo) global R; global C; global Vi; ret = (Vi - Vo) / (R * C); endfunction Vo_numeric = zeros(size(t)); n = 1; for i = t if (n == 1) Vo_numeric(1) = 0; % condiciones iniciales nulas else % integramos numéricamente mediante el método de Euler Vo_numeric(n) = Vo_numeric(n - 1) + h * f(Vo_numeric(n - 1)); endif n = n + 1; endfor % visualizamos ambas soluciones (en rojo la solución analítica y en azul la solución numérica) plot(t, Vo_analytic, "r", t, Vo_numeric, "b");
La solución analítica es la más exacta pero también es la más complicada de obtener ya que requiere del uso de ecuaciones diferenciales mientras que la solución numérica no es la más exacta pero es más sencilla de obtener.
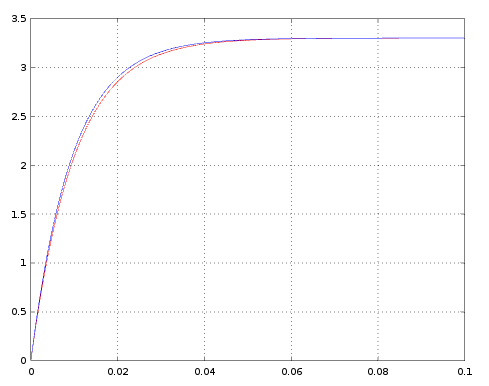
En rojo puede verse la solución analítica y en azul la solución numérica. Hay que tener en cuenta que se ha utilizado el método de Euler de integración numérica que no es, ni de lejos, de los mejores métodos de integración. Con otros métodos de integración, como el Runge-Kutta de cuarto orden (RK4) se obtendrían resultados mucho mejores y con un error mucho menor con respecto de la solución analítica.
Espero que les haya resultado interesante.
[ 3 comentarios ] ( 43527 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 6457 )
( 3 / 6457 )Transmitir una señal modulada en FM dentro de la banda de frecuencias de la FM comercial utilizando FPGAs es un tópico ampliamente cubierto en decenas de webs y vídeos online pero que en pocos casos es desgranado y explicado de forma entendible y rigurosa. A lo largo de este post se desarrollará tanto la base teórica como una prueba de concepto de un transmisor FM basado en FPGA.
Los fundamentos
La modulación FM consiste en hacer variar la frecuencia de la señal que estamos mandando a la antena en función de la amplitud de la señal moduladora (sonido, por ejemplo). El rango de frecuencias reservado para emisoras comerciales de audio abarca desde los 87.5 MHz hasta los 108 MHz (es el rango que recoge cualquier receptor FM analógico) con una profundidad de modulación de +- 75 KHz. Esto significa que si queremos emitir en la frecuencia de 100 MHz debemos hacer variar la frecuencia entre 99.925 MHz y 100.075 MHz en función de la amplitud de la señal moduladora.
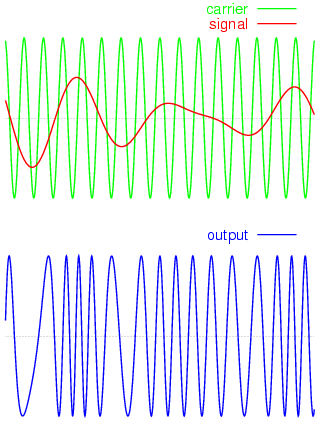
(imagen extraida de Wikipedia, con licencia Creative Commons Attribution - Share Alike 2.0, autor Gvf)
Generar la señal en el dominio digital
Intentar hacer un transmisor FM utilizando una FPGA nos hace chocar, a priori, con un primer impedimento: Poder generar una señal que varíe de frecuencia de una forma tan ligera. Hay que tener en cuenta que con una anchura de modulación de 150 KHz (75 KHz + 75 KHz) y asumiendo una señal sonora muestreada a 16 bits tenemos que la variación de la señal de salida de la antena debe de ser en pasos de:
$${150000 \over {2^{16}}} = {150000 \over 65536} = 2.2888 Hz$$
Esos son muy pocos hercios. En el dominio digital lo habitual para modificar la frecuencia de una señal es multiplicarla por una constante (mediante un PLL) o dividirla entre una constante (mediante un divisor de frecuencias). Los PLLs son circuitos híbridos (entre analógicos y digitales), no son todo lo rápido que nos gustaría (lo normal es que un PLL necesite varios ciclos hasta estabilizarse en la frecuencia deseada), normalmente trabajan con factores constantes (no variables como en nuestro caso) y no están siempre disponibles en las FPGAs para uso directo del usuario. Los divisores de frecuencia son más fáciles de hacer (no dejan de ser baterías de biestables) pero, como su propio nombre indica, sólo son capaces de dividir la frecuencia entre un valor entero.
Acumuladores de fase
Existe, sin embargo, una forma bastante ingeniosa para la síntesis directa de señales digitales sin necesidad del uso de PLLs ni de divisores de frecuencia: los acumuladores de fase. Un acumulador de fase es una de las partes que integran un oscilador digital basado en tabla de ondas. Imaginemos que queremos generar una onda senoidal mediante una tabla de ondas.
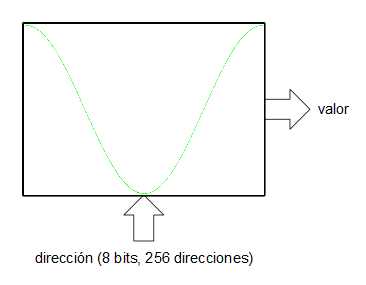
Asumiremos, por simplificar, que la tabla de la onda (realmente sería una ROM o una RAM) tiene un tamaño de 256 muestras ($2^8$). Por otro lado tenemos un registro (al que llamaremos acumulador de fase) de 16 bits y lo que hacemos es indexar la tabla de ondas utilizando los 8 bits más significativos del acumulador de fase. Las entradas D de los biestables de este registro se conectan a la salida un sumador que suma las salidas Q (el valor actual de registro) más un valor de entrada de 16 bits. En cada flanco de subida del reloj del sistema el registro (el acumulador de fase) se carga con el valor de las entradas D procedentes del sumador. En cada tick de reloj el acumulador va acumulando el valor de la entrada de 16 bits.
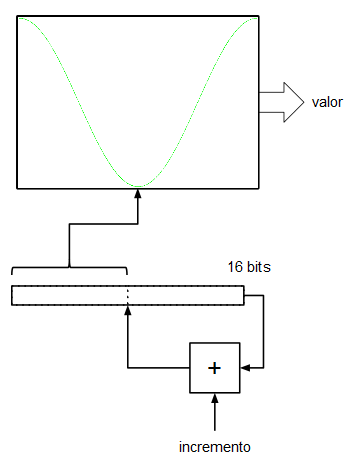
Si en la entrada de 16 bits ponemos un 0, el registro se quedará "quieto", no cambiará su valor y, por tanto la salida de datos de la ROM indexada por dicho registro sacará un valor constante (frecuencia de 0 Hz). Si en la entrada de 16 bits ponemos un 1, en registro se irá incrementando de 1 en 1, sin embargo, como lo que indexa a la tabla de valores son los 8 bits más significativos, este índice sólo avanzará cada 256 pulsos de reloj del sistema. Esto significa que con una frecuencia de reloj de 32 KHz, nuestro oscilador generaría una señal con una frecuencia de:
$${32000 \over 256} = 125 Hz$$
Yéndonos al otro extremo, si en la entrada de 16 bits metemos un valor de $2^{15} = 32768$, el acumulador de fase, al ser de 16 bits, se desbordará cada dos ciclos de reloj: el acumulador de fase generará la secuencia de valores 0, 32768, 0, 32768, 0, 32768, etc. que, a su vez, indexarán los valores mínimo y máximo de la onda senoidal que tenemos en la tabla. Esto significa que la salida del oscilador ha alcanzado su frecuencia máxima (su frecuencia de Nyquist, de 16 KHz).
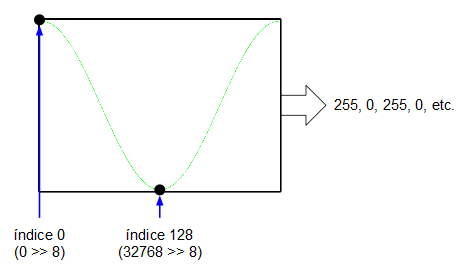
Como se puede comprobar, los incrementos en los pasos son lineales por lo que podemos establecer una especie de regla de tres para el cálculo de la frecuencia de salida de nuestro oscilador imaginario:
$$I_{acumulador fase} = {f_{deseada} \over 32000} \times 2^{16}$$
Vemos que si frecuencia_deseada = 0, entonces incremento_acumulador_fase = 0. Si frecuencia_deseada = 16000 (la frecuencia Nyquist, para 32 KHz), entonces:
$$I_{acumulador fase} = {16000 \over 32000} \times 2^{16} = {1 \over 2} \times 2^{16} = 2^{15} = 32768$$
Para 440 Hz (la nota LA de la cuarta octava del piano) tenemos que:
$$I_{acumulador fase} = {440 \over 32000} \times 2^{16} = 901.12$$
En estos casos, cuando el resultado es fraccionario, hay dos opciones: O quedarse con la parte entera (redondeando o truncando, incremento_acumulador_fase = 901), o, si no queremos perder precisión, incrementar el número de bits para reducir el error. Por ejemplo, utilizando un acumulador de fase de 59 bits conseguiríamos un valor de incremento entero (sin parte fraccionaria):
$$I_{acumulador fase} = {440 \over 32000} \times 2^{59} = 7926335344172073$$
De forma general se puede plantear la ecuación de la siguiente manera:
$$I_{acumulador fase} = {f_{deseada} \over f_{muestreo}} \times 2^{bits}$$
Nótese que la cantidad de bits que indexa la tabla de ondas no es relevante. Lo único importante es que la tabla de ondas está indexada por la parte alta del registro acumulador de fase. Como se puede apreciar, con este método es posible generar frecuencias arbitrarias con pasos relativamente pequeños y sólo limitados por el número de bits que utilicemos en el acumulador de fase.
El transmisor
Imaginemos que la frecuencia de muestreo es ahora de 320 MHz y que queremos generar una frecuencia de 100 MHz. Utilizando un acumulador de fase de 32 bits (la cantidad de bits elegida es arbitraria) tendríamos que:
$$I_{acumulador fase} = {100000000 \over 320000000} \times 2^{32} = 1342177280$$
Como se comentó antes, la cantidad de bits de resolución a la hora de indexar la tabla de ondas no es relevante a efectos de frecuencia (aunque sí a efectos de distorsión armónica y de relación señal/ruido). En nuestro caso, como no disponemos de un DAC sino que vamos a generar una señal cuadrada directamente, en teoría lo que necesitamos es una tabla con una onda cuadrada de tal forma que cuando esté en el máximo emita un 1 y cuando esté en el mínimo emita un 0.
Si asumimos que en la tabla de ondas vamos a meter una onda cuadrada con un ciclo de trabajo del 50% (perfectamente cuadrada), esto significará que la mitad de la tabla de ondas va a estar al valor mínimo (0 por ejemplo) y la otra mitad al valor máximo (255 por ejemplo, si es una ROM de 8 bits sin signo). Si al final vamos a traducir la salida de la tabla de ondas como un 0 si está en el valor mínimo y como un 1 si está en el valor máximo, es obvio que la salida de la tabla de ondas coincidirá con el valor del bit más significativo del acumulador de fase.
Y he aquí la "magia" del invento: Usando un único registro con un sumador podemos hacer un oscilador de onda cuadrada para el que podemos controlar la frecuencia de forma precisa entre 0 Hz y la mitad de la frecuencia de reloj. La precisión a la hora de ajustar la frecuencia nos la dará la cantidad de bits que usemos.
El jittering
Cualquier incremento en el acumulador de fase que no sea potencia de dos va a generar un efecto jitter en la señal de salida haciendo que ésta muchas veces diste de ser una señal cuadrada perfecta. Esto, como es obvio, provocará que la cantidad de armónicos que se generen se dispare. Vamos a verlo con un ejemplo.
Imaginemos el caso anterior: 320 MHz de frecuencia de reloj, un acumulador de fase de 32 bits y un incremento para el acumulador de fase igual a 1342177280. Aplicando este acumulador de fase obtenemos la siguiente salida (correspondiente al bit más significativo):
1 1 0 1 1 0 1 1 0 0 1 0 0 1 0 0 ... la secuencia se repite indefinidamente
Como se puede observar esta secuencia de bits dista mucho de parecerse a una señal cuadrada con ciclo de trabajo del 50%, en concreto genera tres pulsos anchos más juntos y luego dos pulsos estrechos más separados. Sin embargo si hacemos el análisis de Fourier de esta secuencia, tratándola como si fuese una señal, calculándole la transformada de Fourier usando un software numérico como Octave:
octave> abs(fft([1 1 0 1 1 0 1 1 0 0 1 0 0 1 0 0])) ans = 8.00000 1.79995 0.00000 1.01959 0.00000 5.12583 0.00000 1.20269 0.00000 1.20269 0.00000 5.12583 0.00000 1.01959 0.00000 1.79995
Vemos que la transformada de Fourier resultante es efectivamente simétrica (quitando la posición 0, que es la componente de continua), al tratarse de una señal real, y que, descartando la componente de continua (el índice 0 del vector), hay un máximo en el índice 5 del vector. Por las propiedades de la transformada de Fourier en este caso la posición 8 (el centro del vector y el centro de simetría) se corresponde con la frecuencia Nyquist que, al ser la frecuencia de reloj de 320 MHz, sería de 160 MHz (la mitad de la frecuencia del reloj). El máximo situado en la posición 5 del vector se corresponderá, siguiendo una regla de tres, con la frecuencia de:
$${{160000000 \times 5} \over 8} = 100000000 = 100 MHz$$
En efecto, la frecuencia fundamental (el máximo en la transformada de Fourier) de la señal de salida es de 100 MHz, que era nuestro objetivo, aunque como se puede ver en el análisis de Fourier, también se emitirán armónicos de 20 MHz (el valor 1.79995 se corresponde con la frecuencia ${{160 \times 1} \over 8}$), de 60 MHz (${{160 \times 3} \over 8}$) y de 140 MHz (${{160 \times 7} \over 8}$), aunque de menor amplitud.
Implementación y prueba de concepto
Como se va a emitir el sonido por radio FM y aún no disponemos de un ADC que permita la lectura de una fuente externa de audio, se generará la señal de audio dentro de la propia FPGA.
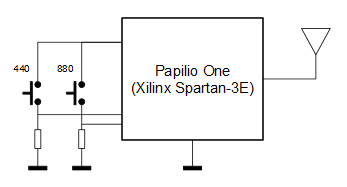
El sistema consta de dos entradas conectadas a sendos botones y que permiten seleccionar la frecuencia del tono a transmitir: cuando no se pulsa ningún botón no se modula (se genera la portadora sin modular), cuando se pulsa el botón “440” la portadora se modula con una señal cuadrada de 440 Hz (nota LA en la cuarta octava del piano), mientras que si se pulsa el botón “880” la portadora se modula con una señal cuadrada de 880 Hz (nota LA en la quinta octava del piano).
La única salida del sistema es la salida de la antena, que va a un trozo de cable que se coloca al aire. No es necesario nada más si vamos a colocar el receptor a pocos metros de la FPGA. En el caso de que queramos conectar la salida a una antena real y que queramos más potencia habría que colocar circuitos acondicionadores y/o amplificadores a la salida y, sobretodo, filtros: hay que recordar que la señal de salida es una onda cuadrada repleta de armónicos.
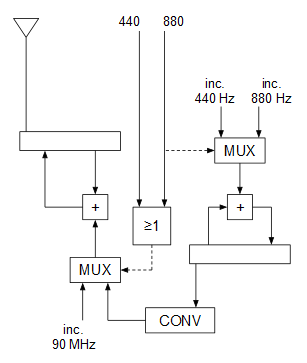
En reposo, las entradas “440” y “880” valen 0, por lo que el MUX inferior selecciona la entrada del incremento correspondiente a los 90 MHz (portadora sin modular). Cuando se pulsa sólo el botón “440” el MUX inferior deja pasar la señal moduladora (ya convertida en secuencias de incrementos en lugar de en 0 y 1) a la entrada del oscilador para modularlo, y cuando se pulsa el botón “880” ocurre lo mismo con el MUX inferior y, además, al cambiar la entrada de selección del MUX superior, cambia el incremento del oscilador que genera la señal moduladora para que genere 880 Hz en lugar de 440 Hz.
El módulo combinacional CONV convierte la entrada de 1 bit (0 o 1) proveniente del oscilador de 440 u 880 Hz, en una salida de 32 bits que es el incremento de fase de correspondiente a cada nivel de la señal moduladora:
0 --> 1341058799
1 --> 1343295761
En este caso se ha realizado una implementación sobre una FPGA Spartan-3E de Xilinx con un reloj externo de 32 MHz (papilio one). Las Spartan-3E disponen de varios DCM (Digital Clock Managers) que permiten subir la frecuencia de reloj mediante multiplicadores. En este caso, con un reloj a 32 MHz la máxima frecuencia que se puede alcanzar es de 288 MHz, por lo que ajustamos los cálculos a dicha frecuencia y asumiendo que vamos a transmitir en la banda de 90 MHz.
$$I_{acumulador fase} = {90000000 \over 288000000} \times 2^{32} = 1342177280$$
Como la señal moduladora (los tonos de 440 y 880 Hz) van a ser también ondas cuadradas, sólo hay que calcular los incrementos para el 0 y el 1 de la señal moduladora (en este caso no hay valores intermedios). El 0 de la señal moduladora lo asociaremos a 89,925 MHz y el 1 de la señal moduladora lo asociaremos a 90,075 MHz (recordemos que la profundidad de modulación en la FM comercial es de 75 KHz).
$$I_{89.925} = {89925000 \over 288000000} \times 2^{32} \approx 1341058799$$
$$I_{90.075} = {90075000 \over 288000000} \times 2^{32} \approx 1343295761$$
A continuación puede verse el código fuente:
library ieee; use ieee.std_logic_1164.all; use ieee.numeric_std.all; entity FMTransmitter is port ( Clk : in std_logic; Reset : in std_logic; Button440 : in std_logic; Button880 : in std_logic; AntOut : out std_logic ); end entity; architecture Architecture1 of FMTransmitter is component Oscillator is generic ( NBits : integer := 32 ); port ( IncrementIn : in std_logic_vector(31 downto 0); Clk : in std_logic; Reset : in std_logic; DataOut : out std_logic ); end component; component Mux2Inputs is generic ( NBits : integer := 32 ); port ( Sel : in std_logic; DataIn0 : in std_logic_vector((NBits - 1) downto 0); DataIn1 : in std_logic_vector((NBits - 1) downto 0); DataOut : out std_logic_vector((NBits - 1) downto 0) ); end component; signal Mux1Out : std_logic_vector(31 downto 0); signal Mux1Sel : std_logic; signal ConvOut : std_logic_vector(31 downto 0); signal ConvIn : std_logic; signal Mux2Out : std_logic_vector(31 downto 0); begin RadioOsc : Oscillator generic map ( NBits => 32 ) port map ( Clk => Clk, Reset => Reset, IncrementIn => Mux1Out, DataOut => AntOut ); Mux1Sel <= Button440 or Button880; Mux1 : Mux2Inputs generic map ( NBits => 32 ) port map ( Sel => Mux1Sel, DataIn0 => std_logic_vector(to_unsigned(1342177280, 32)), -- center freq = 90.0 MHz DataIn1 => ConvOut, DataOut => Mux1Out ); -- center freq - 75 KHz when 0 -- center freq + 75 KHz when 1 ConvOut <= std_logic_vector(to_unsigned(1341058799, 32)) when (ConvIn = '0') else std_logic_vector(to_unsigned(1343295761, 32)); AudioOsc : Oscillator generic map ( NBits => 32 ) port map ( Clk => Clk, Reset => Reset, IncrementIn => Mux2Out, DataOut => ConvIn ); Mux2 : Mux2Inputs generic map ( NBits => 32 ) port map ( Sel => Button880, DataIn0 => std_logic_vector(to_unsigned(6562, 32)), -- 440 Hz DataIn1 => std_logic_vector(to_unsigned(13124, 32)), -- 880 Hz DataOut => Mux2Out ); end architecture;
Tanto el oscilador de salida (el de alta frecuencia) como el oscilador de audio se han implementado usando el mismo componente “Oscillator.vhd”.
library ieee; use ieee.std_logic_1164.all; use ieee.numeric_std.all; use ieee.std_logic_signed.all; entity Oscillator is generic ( NBits : integer := 32 ); port ( IncrementIn : in std_logic_vector(31 downto 0); Clk : in std_logic; Reset : in std_logic; DataOut : out std_logic ); end entity; architecture Architecture1 of Oscillator is component Reg is generic ( NBits : integer := 32 ); port ( Enable : in std_logic; Clk : in std_logic; DataIn : in std_logic_vector((NBits - 1) downto 0); DataOut : out std_logic_vector((NBits - 1) downto 0) ); end component; signal MuxOut : std_logic_vector((NBits - 1) downto 0); signal RegOut : std_logic_vector((NBits - 1) downto 0); begin PhaseAcc : Reg generic map ( NBits => NBits ) port map ( Enable => '1', Clk => Clk, DataIn => MuxOut, DataOut => RegOut ); MuxOut <= (others => '0') when (Reset = '1') else (RegOut + IncrementIn); DataOut <= RegOut(NBits - 1); end architecture;
El tipo de sumador
En otros proyectos FPGA anteriormente abordados en este blog, cada vez que hacía falta un sumador se tiraba de un sumador estándar implementado mediante lógica combinatoria (“Adder.vhd”). Hasta ahora se ha hecho así por razones pedagógicas. En este caso, sin embargo, al estar el reloj a una frecuencia extremadamente alta para la FGPA ha sido necesario el uso del operador “+”. Este operador garantiza “la mejor implementación” de la suma para la plataforma y esto se traduce, en el caso del Spartan-3E y en el caso de la mayoría de las FPGAs existentes, en que se va a hacer uso de sumadores que ya se encuentran integrados (“hardwired”) en el sustrato de todas las FPGA (todos los fabricantes los incluyen, de mayor o menor cantidad de bits).
¿Qué ventajas tienen estos sumadores con respecto al sumador que hemos estado usando hasta ahora? La principal diferencia es que en nuestro “Adder.vhd” el acarreo es en cascada, mientras que los sumadores implementados a fuego en las FPGAs están basados siempre en circuitos CLA (Carry Look Ahead), que permiten precalcular los acarreos de cada bit sin necesidad de que estén calculados los bits anteriores. Aún siendo circuitos combinacionales tanto los unos como los otros, el tiempo de propagación del resultado en el caso de sumadores con CLA es mucho menor que en el caso de sumadores con acarreo en cascada (como el “Adder.vhd” que hemos usado hasta ahora en los proyectos).
En nuestro caso concreto se da además la circunstancia que, con un reloj a 288 MHz, el sumador con acarreo en cascada (el “Adder.vhd” de siempre) da problemas de timing o, lo que es lo mismo, “no le da tiempo de sumar tan rápido” y no queda otra opción que tirar del operador “+” (cosa que, por otro lado, es lo recomendable ya que se garantiza siempre la mejor implementación).
Vídeo
A continuación un pequeño fragmento de vídeo donde se puede ver y escuchar el invento en funcionamiento. La calidad del audio es bastante baja: usé mi radio-despertador como receptor, en el receptor del móvil se oye mucho mejor… pero no hubiese podido grabarlo :-)
Espero que haya resultado interesante. Todo el código fuente se puede descargar de la sección soft.
[ añadir comentario ] ( 3517 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 6085 )
( 3 / 6085 )Gracias a su bajo costo, su relativo poco consumo y su facilidad de programación, los leds RGB basados en el chip WS2812 se están convirtiendo en estándar de facto para leds RGB. A lo largo de esta mini serie de posts se implementará sobre FPGA una interface que facilite el acceso a estos leds abstrayendo las complejidades de su programación.
Motivación
El WS2812 es un led RGB con interface digital mediante tren de pulsos modulado en anchura (PWM) a través de una única línea serie asíncrona. Cada led acepta 24 bits, cuando el tren de pulsos PWM supera esa cantidad de bits, el led envía los bits “sobrantes” a través de otro de sus pines, de esta forma pueden encadenarse tantos leds RGB en serie como se quiera. Aquí puede descargarse la hoja de datos del fabricante.
El tren de pulsos debe tener unos tiempos muy específicos.
- Para mandar un 0 hay que poner la entrada a nivel alto durante 350 ns y luego a nivel bajo durante 800 ns.
- Para mandar un 1 hay que poner la entrada a nivel alto durante 700 ns y luego a nivel bajo durante 600 ns.
Con estos tiempos, con un microcontrolador de gama media o baja, si no tenemos una salida específica que soporte este protocolo hay que recurrir a “trucos”:
- Bitbanging: Lo bueno es que funciona en cualquier micro que tenga GPIO (todo tienen pines GPIO), lo malo es que los tiempos que hay que manejar obligan a inhibir las interrupciones y dejar de hacer el resto de tareas cada vez que el micro quiera refrescar el estado de los leds. Esta es la solución más utilizada actualmente.
- Aprovechar la interface SPI o I2S que tenga el microcontrolador para simular el tren de pulsos: Lo bueno es que es una solución menos “soft” que la anterior pero es una solución muy específica que debe ser programada en función de las características de cada micro y que nos obliga a prescindir de dicho interface (SPI o I2S) de la forma habitual. Por otro lado, aunque se utilicen controladores DMA internos del microcontrolador para aligerar la carga de la CPU, lo cierto es que un controlador DMA no deja de ser un máster de bus más, por lo que siempre provoca un incremento en los estados de espera de la RAM del procesador.
Solución hardware
La idea es utilizar una FPGA para abstraer el acceso a los WS2812. La FPGA implementará una RAM que hará las veces de RAM de vídeo: De cara a los neopixels habrá una máquina de estados encargada de generar el tren de pulsos necesario para representar en los neopixels conectados el contenido de la RAM interna. De cara al procesador la FPGA se mostrará como una RAM con interface SPI estándar. De esta forma el procesador para iluminar un led RGB lo que hará será escribir el valor RGB en la posición correspondiente de la RAM de la FPGA. Los tres primeros bytes se corresponden con el primer pixel (formato GRB), los tres siguiente con el siguiente píxel y así sucesivamente.
Primera iteración
Como primera iteración de la solución se planteará la implementación sólo del interface con los leds RGB y que por ahora lea los datos de una ROM simulada dentro de la FPGA. La conexión SPI se dejará, por tanto, para la segunda iteración del proyecto.
Ruta de datos
La ruta de datos planteada para el interface de la FPGA con los neopixels es la siguiente:
A continuación se enumeran los elementos de forma agrupada.
La memoria ROM
Por ahora es una ROM ya que sólo se va a emitir su contenido y no será aún accesible mediante SPI.
library ieee; use ieee.std_logic_1164.all; use ieee.numeric_std.all; entity Rom is port ( AddressIn : in std_logic_vector(12 downto 0); DataOut : out std_logic_vector(7 downto 0) ); end entity; architecture Architecture1 of Rom is type RomType is array (0 to 8191) of std_logic_vector(7 downto 0); constant Data : RomType := ( -- format = GRB "10111010", -- first pixel = green "00100110", "00001000", "00000000", -- second pixel = red "10001000", "00110011", "01000000", -- third pixel = blue "11111111", "10010110", "10000000", -- fourth pixel = yellow "10000000", "00000000", others => "00000000" ); begin DataOut <= Data(to_integer(unsigned(AddressIn))); end architecture;
Registro de desplazamiento (SR)
Se trata de un registro de desplazamiento estándar con multiplexor de carga. Cuando la entrada LOAD está a 1 el multiplexor dirige los datos de la ROM hacia la entrada del registro, mientras que cuando la entrada LOAD está a 0 el multiplexor dirige los datos del desplazador de 1 bit a la izquierda.
library ieee; use ieee.std_logic_1164.all; use ieee.numeric_std.all; entity ShiftReg is generic ( NBits : integer := 8 ); port ( Clk : in std_logic; Enable : in std_logic; BitOut : out std_logic; DataIn : in std_logic_vector((NBits - 1) downto 0); Load : in std_logic ); end entity; architecture Architecture1 of ShiftReg is component Reg is generic ( NBits : integer := 16 ); port ( Enable : in std_logic; Clk : in std_logic; DataIn : in std_logic_vector((NBits - 1) downto 0); DataOut : out std_logic_vector((NBits - 1) downto 0) ); end component; signal InputMuxOut : std_logic_vector((NBits - 1) downto 0); signal DataOut : std_logic_vector((NBits - 1) downto 0); begin R : Reg generic map ( NBits => NBits ) port map ( Enable => Enable, Clk => Clk, DataIn => InputMuxOut, DataOut => DataOut ); BitOut <= DataOut(7); InputMuxOut <= DataIn when (Load = '1') else DataOut(6 downto 0) & '0'; end architecture;
Contador con un único límite (BC y ADDR)
Los contadores BC (Bit Counter) y Addr son dos instancias de un mismo contador. El contador implementado permite definir en tiempo de compilación VHDL tanto el valor de inicialización como el valor límite así como el valor de incremento (que puede ser negativo en complemento a dos). En el caso del contador ADDR el valor de inicio es 0 y el incremento es +1. El caso del contador BC es más laxo ya que no se necesita el valor de la cuenta: sólo hace falta saber si se ha llegado al final.
library ieee; use ieee.std_logic_1164.all; use ieee.numeric_std.all; entity FixedLimitCounter is generic ( NBits : integer := 16; LimitValue : integer := 0; ResetValue : integer := 1000; Increment : integer := -1 ); port ( Clk : in std_logic; Enable : in std_logic; Reset : in std_logic; LimitReached : out std_logic; DataOut : out std_logic_vector((NBits - 1) downto 0) ); end entity; architecture Architecture1 of FixedLimitCounter is component Reg is generic ( NBits : integer := 16 ); port ( Enable : in std_logic; Clk : in std_logic; DataIn : in std_logic_vector((NBits - 1) downto 0); DataOut : out std_logic_vector((NBits - 1) downto 0) ); end component; component Adder is generic ( NBits : integer := 16 ); port ( A : in std_logic_vector((NBits - 1) downto 0); B : in std_logic_vector((NBits - 1) downto 0); Y : out std_logic_vector((NBits - 1) downto 0) ); end component; signal TCOut : std_logic_vector((NBits - 1) downto 0); signal AdderOut : std_logic_vector((NBits - 1) downto 0); signal InputMuxOut : std_logic_vector((NBits - 1) downto 0); signal LimitReachedPulse : std_logic; signal LimitReachedDBus : std_logic; signal LimitReachedQBus : std_logic; begin C : Reg generic map ( NBits => NBits ) port map ( Enable => Enable, Clk => Clk, DataIn => InputMuxOut, DataOut => TCOut ); A : Adder generic map ( NBits => NBits ) port map ( A => std_logic_vector(to_signed(Increment, NBits)), B => TCOut, Y => AdderOut ); InputMuxOut <= std_logic_vector(to_signed(ResetValue, NBits)) when (Reset = '1') else AdderOut; LimitReachedPulse <= '1' when (TCOut = std_logic_vector(to_signed(LimitValue, NBits))) else '0'; DataOut <= TCOut; -- LimitReached D flip-flop process (Clk) begin if (Clk'event and (Clk = '1')) then LimitReachedQBus <= LimitReachedDBus; end if; end process; LimitReachedDBus <= '0' when (Reset = '1') else (LimitReachedQBus or LimitReachedPulse); LimitReached <= LimitReachedQBus; end architecture;
Contador de límite variable (TC)
El contador TC (Time Counter) es un contador parecido al anterior. La diferencia es que el límite siempre es 0, el incremento es siempre -1 y el valor de inicialización de la cuenta es la salida de un multiplexor de 5 entradas. Este contador se utiliza para medir tiempos. En el caso de los neopixels hay que medir cinco tiempos: el valor alto para el 0 (T0H), el valor bajo para el 0 (T0L), el valor alto para el 1 (T1H), el valor bajo para el 1 (T1L) y el tiempo de pausa entre frames que, en el caso de los neopixels, debe ser de, al menos, 50 microsegundos.
library ieee; use ieee.std_logic_1164.all; use ieee.numeric_std.all; entity Fixed5LimitsCounter is generic ( NBits : integer := 16; Limit0 : integer := 10; Limit1 : integer := 20; Limit2 : integer := 30; Limit3 : integer := 40; Limit4 : integer := 50 ); port ( Clk : in std_logic; Enable : in std_logic; Reset : in std_logic; LimitReached : out std_logic; LimitSelect : in std_logic_vector(2 downto 0) ); end entity; architecture Architecture1 of Fixed5LimitsCounter is component Reg is generic ( NBits : integer := 16 ); port ( Enable : in std_logic; Clk : in std_logic; DataIn : in std_logic_vector((NBits - 1) downto 0); DataOut : out std_logic_vector((NBits - 1) downto 0) ); end component; component Adder is generic ( NBits : integer := 16 ); port ( A : in std_logic_vector((NBits - 1) downto 0); B : in std_logic_vector((NBits - 1) downto 0); Y : out std_logic_vector((NBits - 1) downto 0) ); end component; signal LimitMuxOut : std_logic_vector((NBits - 1) downto 0); signal TCOut : std_logic_vector((NBits - 1) downto 0); signal AdderOut : std_logic_vector((NBits - 1) downto 0); signal InputMuxOut : std_logic_vector((NBits - 1) downto 0); signal LimitReachedPulse : std_logic; signal LimitReachedDBus : std_logic; signal LimitReachedQBus : std_logic; begin TC : Reg generic map ( NBits => NBits ) port map ( Enable => Enable, Clk => Clk, DataIn => InputMuxOut, DataOut => TCOut ); A : Adder generic map ( NBits => NBits ) port map ( A => std_logic_vector(to_signed(-1, NBits)), B => TCOut, Y => AdderOut ); LimitMuxOut <= std_logic_vector(to_unsigned(Limit0, NBits)) when (LimitSelect = "000") else std_logic_vector(to_unsigned(Limit1, NBits)) when (LimitSelect = "001") else std_logic_vector(to_unsigned(Limit2, NBits)) when (LimitSelect = "010") else std_logic_vector(to_unsigned(Limit3, NBits)) when (LimitSelect = "011") else std_logic_vector(to_unsigned(Limit4, NBits)); InputMuxOut <= LimitMuxOut when (Reset = '1') else AdderOut; LimitReachedPulse <= '1' when (TCOut = std_logic_vector(to_signed(0, NBits))) else '0'; -- LimitReached D flip-flop process (Clk) begin if (Clk'event and (Clk = '1')) then LimitReachedQBus <= LimitReachedDBus; end if; end process; LimitReachedDBus <= '0' when (Reset = '1') else (LimitReachedQBus or LimitReachedPulse); LimitReached <= LimitReachedQBus; end architecture;
Máquina de estados
La máquina de estados que se ha realizado consta de 16 estados (cabe justito en 4 biestables si codificamos los estados de forma binaria estándar). Se trata de una máquina de estados de tipo Moore en la que la salida depende del estado actual y el estado siguiente depende del estado actual y de las entradas:
La implementación de una máquina de Moore en VHDL es sistemática:
library ieee; use ieee.std_logic_1164.all; entity FSM is port ( -- inputs Clk : in std_logic; Reset : in std_logic; DrawDisplay : in std_logic; TCLimitReached : in std_logic; BitCounterLimitReached : in std_logic; AddrLimitReached : in std_logic; CurrentBit : in std_logic; -- outputs AddrEnable : out std_logic; AddrReset : out std_logic; RAMEnable : out std_logic; SRLoad : out std_logic; SREnable : out std_logic; BitCounterEnable : out std_logic; BitCounterReset : out std_logic; TCLimitSelect : out std_logic_vector(2 downto 0); -- 000=t0h, 001=t0l, 010=t1h, 011=t1l, 1XX=50us TCEnable : out std_logic; TCReset : out std_logic; NeopixelOutput : out std_logic ); end entity; architecture Architecture1 of FSM is signal QBus : std_logic_vector(3 downto 0); signal DBus : std_logic_vector(3 downto 0); begin process (Clk, Reset) begin if (Clk'event and (Clk = '1')) then if (Reset = '1') then QBus <= (others => '0'); else QBus <= DBus; end if; end if; end process; -- next state logic DBus <= "0001" when ((QBus = "0000") and (DrawDisplay = '1')) else "0010" when ((QBus = "0001") or ((QBus = "1101") and (AddrLimitReached = '0'))) else "0011" when (QBus = "0010") else "0100" when ((QBus = "0011") or (QBus = "1011")) else "0101" when (QBus = "0100") else "0110" when ((QBus = "0101") or ((QBus = "0110") and (TCLimitReached = '0'))) else "0111" when ((QBus = "0110") and (TCLimitReached = '1')) else "1000" when ((QBus = "0111") or ((QBus = "1000") and (TCLimitReached = '0'))) else "1001" when ((QBus = "1000") and (TCLimitReached = '1')) else "1010" when (QBus = "1001") else "1011" when ((QBus = "1010") and (BitCounterLimitReached = '0')) else "1100" when ((QBus = "1010") and (BitCounterLimitReached = '1')) else "1101" when (QBus = "1100") else "1110" when ((QBus = "1101") and (AddrLimitReached = '1')) else "1111" when ((QBus = "1110") or ((QBus = "1111") and (TCLimitReached = '0'))) else "0000" when ((QBus = "1111") and (TCLimitReached = '1')) else "0000"; -- output logic AddrEnable <= '1' when ((QBus = "0001") or (QBus = "1100")) else '0'; AddrReset <= '1' when (QBus = "0001") else '0'; RAMEnable <= '1' when (QBus = "0010") else '0'; SRLoad <= '1' when (QBus = "0011") else '0'; SREnable <= '1' when ((QBus = "0011") or (QBus = "1011")) else '0'; BitCounterEnable <= '1' when ((QBus = "0011") or (QBus = "1001")) else '0'; BitCounterReset <= '1' when (QBus = "0011") else '0'; TCLimitSelect <= "000" when ((QBus = "0101") and (CurrentBit = '0')) else "001" when ((QBus = "0111") and (CurrentBit = '0')) else "010" when ((QBus = "0101") and (CurrentBit = '1')) else "011" when ((QBus = "0111") and (CurrentBit = '1')) else "100" when (QBus = "1110") else "000"; TCEnable <= '1' when ((QBus = "0101") or (QBus = "0110") or (QBus = "0111") or (QBus = "1000") or (QBus = "1110") or (QBus = "1111")) else '0'; TCReset <= '1' when ((QBus = "0101") or (QBus = "0111") or (QBus = "1110")) else '0'; NeopixelOutput <= '1' when (QBus = "0110") else '0'; end architecture;
Como se puede observar hay una señal de entrada adicional que no se encuentra reflejada en la ruta de datos: DRAW. La máquina de estados, al arrancar se pone en el estado 0 (el estado de reset) y permanece en ese estado hasta que la entrada DRAW se ponga a 1, en ese momento es cuando se desencadena todo el proceso (le lee la ROM y se manda bit a bit usando el PWM específico de los neopixels). Cuando terminan de mandarse todos los bytes, la máquina de estados espera el tiempo de pausa (mínimo 50 microsegundo) y vuelve al estado 0. Estado en el que se queda a menos que desde fuera se le vuelva a indicar que dibuje de nuevo (DRAW=1).
Nótese también que la máquina de estados está pensada para interactuar con una RAM ya que el estado 2 pone a 1 la línea ENABLE de la RAM. Esta línea no se encuentra en esta implementación conectada a nada (la ROM no tiene ENABLE, es estática). Se ha dejado ya que en su momento, cuando se utilice una RAM sí que será necesario.
Ajuste de los tiempos
Los tiempos de nivel alto y nivel bajo en función del bit que se envía son críticos en el caso del WS2812. Como se puede ver en el grafo de la máquina de estados el tiempo que está a nivel alto la salida depende exclusivamente del tiempo que permanece la máquina de estados en el estado 6. Dicho tiempo viene determinado por los tiempos T0H y T1H (en función del bit que se esté mandando). El problema viene con el tiempo que debe estar la salida a nivel bajo (T0L y T1L):
- Cuando estamos dentro de los 8 bits del registro de desplazamiento y no es necesario realizar una carga en memoria, además del estado 8 en el que se espera el tiempo T0L o T1L, la máquina de estados pasa por otros estados: 7, 9, 10, 11, 4 y 5 (6 estados adicionales).
- Cuando es necesario cargar el siguiente byte de la memoria en el registro de desplazamiento la cantidad de estados por los que pasa la máquina teniendo la salida a nivel bajo (tiempos T0L y T1L) además del estado 8 son los estados: 7, 9, 10, 12, 13, 2, 3, 4 y 5 (9 estados adicionales).
Teniendo en cuenta que, a 32 MHz, cada estado consume 1 / 32000000 segundos = 31.25 nanosegundos, el desfase de tiempo entre un caso y otro no es trivial. En estos casos hay que echar mano de la tolerancia de las señales de entrada y procurar que la ruta más corta (la primera) entre dentro de la tolerancia de forma negativa para que la ruta más larga (la segunda) caiga dentro de la tolerancia de forma positiva.
Utilizando diferentes testbenchs se consiguieron ajustar los tiempos de esta manera:
T1H
teórico: 700±150 ns (550 a 850 ns)
real con inicio de cuenta en el valor 21:
718750 ps = 718.750 ns = 0.718750 us
T1L
teórico: 600±150 ns (450 a 750 ns)
real con inicio de cuenta en el valor 10:
562500 ps = 562.500 ns = 0.562500 us (ruta “corta”)
656250 ps = 656.250 ns = 0.656250 us (ruta “larga”)
T0H
teórico: 350±150 ns (200 a 500 ns)
real con inicio de cuenta en el valor 9:
343750 ps = 343.750 ns = 0.343750 us
T0L
teórico: 800±150 ns (650 a 950 ns)
real con inicio de cuenta en el valor 16:
750000 ps = 750.000 ns = 0.750000 us (ruta “corta”)
843750 ps = 843.750 ns = 0.843750 us (ruta “larga”)
Estos valores se obtuvieron implementando un reloj a 32 MHz en el testbench (la misma frecuencia del reloj de la placa FPGA Papilio One) y midiendo los tramos correspondientes sobre la simulación.
Implementación física
La implementación física fue la parte más sencilla en este caso. Se asigna la entrada de reloj, se configura la salida para los neopixels y la entrada de reset para la máquina de estados.
El circuito funcionó a la primera :-).
Siguiente entrega
En la siguiente entrega se implementará la parte de interface con el procesador mediante protocolo SPI, simulando una RAM SPI externa.
Todo el código fuente puede descargarse de la sección soft.
[ añadir comentario ] ( 2748 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 3767 )
( 3 / 3767 )En la anterior entrega de la serie se llegó hasta la fase de simulación y se comprobó, usando el software GHDL, el funcionamiento del procesador V1. En esta tercera entrega se ha implementado y probado el diseño en una FPGA real: una Spartan-3E de Xilinx.
>>> Enlace a la segunda entrega de la serie.
Cuando se va a implementar un diseño VHDL sobre un dispositivo real siempre nos podemos topar con problemas o limitaciones inherentes al hardware: por eso el paso final debería ser siempre el sintetizado del código sobre una FPGA. En este caso se optó por el sintetizado sobre una FPGA Spartan-3E de Xilinx, en concreto la que viene incluida en la placa de desarrollo Papilio One.
El problema de la memoria
Todas las FPGAs que hay en el mercado incluyen zonas de su sustrato especialmente diseñadas para implementar memorias RAM y/o ROM. Lo ideal, por lo tanto es que el código VHDL que implemente la ROM y la RAM sea fácilmente detectable o “inferible”, para que el entorno de desarrollo del fabricante utilice estos recursos de forma eficiente y que lo que queremos que sea una RAM se implemente realmente como una RAM y que lo que queremos que sea una ROM se implemente realmente como una ROM.
En el caso del código original que se hizo en la segunda entrega de la serie, a la hora de sintetizar para la FPGA de Xilinx, el entorno de desarrollo ISE detecta y sintetiza la ROM como una ROM pero no es capaz de inferir el código VHDL de la RAM como una RAM: de hecho para la RAM de 8192 palabras de 16 bits sintetiza ¡131072 biestables!
Si nos fijamos en el código VHDL de la RAM de la anterior entrega se puede observar cómo se integró la salida de proposito general (un puerto de salida que se denominó “GPOut”) como salida adicional en la RAM. Para facilitar que el entorno de Xilinx detectase este módulo como una RAM real se pasó la lógica de este puerto GPOut de la RAM al módulo de mas alto nivel “Memory.vhd”. Así mismo se incluyó una entrada “Enable” en el módulo RAM acorde con los estándares de diseño recomendados por los fabricantes. Esta entrada se deja permanentemente a 1 pero facilita al entorno de desarrollo la detección del codigo y su posterior sintetizado como una RAM real.
Ahora “Ram.vhd” es una implementacion más estándar de lo que es una RAM (sin puertos de salida y con una entrada "Enable"):
library ieee; use ieee.std_logic_1164.all; use ieee.numeric_std.all; entity Ram is port ( AddressIn : in std_logic_vector(12 downto 0); DataOut : out std_logic_vector(15 downto 0); DataIn : in std_logic_vector(15 downto 0); WriteEnable : in std_logic; Enable : in std_logic; Clk : in std_logic ); end entity; architecture Architecture1 of Ram is type RamType is array(0 to 8191) of std_logic_vector(15 downto 0); signal Data : RamType; begin process (Clk) begin if ((Clk'event) and (Clk = '1')) then if (Enable = '1') then if (WriteEnable = '1') then Data(to_integer(unsigned(AddressIn))) <= DataIn; end if; DataOut <= Data(to_integer(unsigned(AddressIn))); end if; end if; end process; end architecture;
Y la lógica relacionada con el puerto de salida GPOut se ha trasladado a “Memory.vhd”:
library ieee; use ieee.std_logic_1164.all; use ieee.numeric_std.all; entity Memory is generic ( GPOutAddress : integer := 12288 ); port ( AddressIn : in std_logic_vector(15 downto 0); DataIn : in std_logic_vector(15 downto 0); DataOut : out std_logic_vector(15 downto 0); WriteEnable : in std_logic; GPOut : out std_logic_vector(15 downto 0); Clk : in std_logic ); end entity; architecture Architecture1 of Memory is component Rom is port ( AddressIn : in std_logic_vector(12 downto 0); DataOut : out std_logic_vector(15 downto 0) ); end component; component Ram is port ( AddressIn : in std_logic_vector(12 downto 0); DataOut : out std_logic_vector(15 downto 0); DataIn : in std_logic_vector(15 downto 0); WriteEnable : in std_logic; Enable : in std_logic; Clk : in std_logic ); end component; signal RomOut : std_logic_vector(15 downto 0); signal RamOut : std_logic_vector(15 downto 0); signal GPOutD : std_logic_vector(15 downto 0); signal GPOutQ : std_logic_vector(15 downto 0); begin -- GPOut register process (Clk) begin if ((Clk'event) and (Clk = '1')) then GPOutQ <= GPOutD; end if; end process; GPOutD <= DataIn when (to_integer(unsigned(AddressIn)) = GPOutAddress) else GPOutQ; GPOut <= GPOutQ; -- ROM Rom1 : Rom port map ( -- 8192 words (16 bit) AddressIn => AddressIn(12 downto 0), DataOut => RomOut ); -- RAM Ram1 : Ram port map ( -- 8192 words (16 bit) AddressIn => AddressIn(12 downto 0), DataOut => RamOut, WriteEnable => WriteEnable, Enable => '1', DataIn => DataIn, Clk => Clk ); -- RAM vs ROM multiplexer DataOut <= RomOut when (AddressIn(13) = '0') else -- bit 13 = 0 --> ROM, bit 13 = 1 --> RAM RamOut; end architecture;
Con estas pequeñas modificaciones el entorno de desarrollo ISE de Xilinx sí infiere correctamente la RAM a partir del código VHDL y la implementa como una RAM real dentro de la FPGA.
Estados de espera para la memoria
Introducir este modelo de memoria RAM síncrono tanto para la lectura como para la escritura de datos obliga a introducir un estado de espera antes de cada estado que habilite el registro DATAin en la unidad de control. En concreto es necesario introducir el estado de espera en tres sitios de la máquina de estados: en la secuencia le lectura de instrucciones, en el microcódigo de la instrucción POP y en el microcódigo de la instrucción LOAD.
Para la lectura de instrucciones la secuencia de microcódigo quedaría como sigue:
0. MUX6 := "0", Habilitar PC (El vector de reset es el 0)
1. MUX1 = PC, Habilitar ADDR (Se carga IR con la instrucción apuntada por PC)
2. Estado de espera para la lectura de la memoria
3. Habilitar DATAin
4. Habilitar IR
5. MUX5 := FSM, ALU := inc, MUX4 := PC, Habilitar PC (Se hace PC := PC + 1)
6. EJECUTAR EL MICROCÓDIGO DE LA INSTRUCCIÓN ALMACENADA EN IR
7. Ir al estado 1
El microcódigo de la instrucción POP quedaría así:
POP
MUX1 := SP, Habilitar ADDR
Estado de espera
Habilitar DATAin
Habilitar RA, MUX2 := DATAin
MUX4 := SP, MUX5 := FSM, ALU := dec, Habilitar SP
Mientras que el microcódigo de la instrucción LOAD sería el siguiente:
LOAD
MUX1 := RB, Habilitar ADDR
Estado de espera
Habilitar DATAin
MUX2 := DATAin, Habilitar RA
Estos tres nuevos estados de espera se introducen como nuevos estados en la FSM de la unidad de control.
Blinker
Para probar el procesador se inicializa la ROM (el fichero “Rom.vhd”) con el código máquina asociado al siguiente código ensamblador V1. El programa simplemente cambia de forma alternativa los bits del puerto GPOut (0x0000, 0xFFFF, 0x0000, 0xFFFF, 0x0000, etc.).
# [12288] <-- 0 loadi 12288 op rb, ra, assign loadi 0 store loop: # RA <-- [12288] loadi 12288 op rb, ra, assign load # RA <-- NOT RA op ra, ra, not # [12288] <-- RA store # wait loop loadi 100 op rb, ra, assign waitLoop1: op ra, rb, assign jz waitLoop1End loadi 8192 waitLoop2: jz waitLoop2End op ra, ra, dec j waitLoop2 waitLoop2End: op rb, rb, dec j waitLoop1 waitLoop1End: # end of wait loop j loop
Se trata de un bucle infinito en el que en cada iteración se cambia de estado el puerto GPOut (alternativamente 0x0000 y 0xFFFF) y que, entre iteración e iteración, incluye dos bucles anidados que provocan un retardo significativo y visible entre cada cambio de estado.
El V1 tiene dos entradas de un bit cada una (Clk y Reset) y una salida de 16 bits (GPOut). La entrada de reloj (Clk) se encuentra conectada internamente en la placa Papilio One a un oscilador de cristal de 32MHz, la entrada Reset se mapea al pin A0 de la placa y la salida GPOut se mapea a los pines B0 a B15 (16 bits). Para comprobar que el blinker funciona basta con conectar un led a cualquiera de los pines B0 a B15.
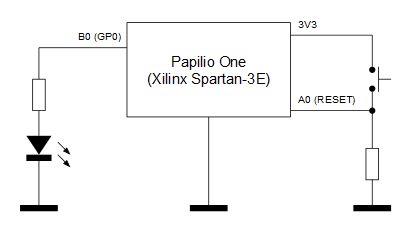
Resultado
Como se puede ver en el siguiente vídeo, nuestro procesador V1 implementado en la FPGA ejecuta perfectamente el código de la ROM.
En la sección soft puede descargarse todo el código VHDL del proyecto.
[ añadir comentario ] ( 2624 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 3684 )
( 3 / 3684 )En esta segunda entrega de la serie se profundiza en el diseño de la unidad de control, en la implementación en VHDL de los diferentes elementos y en la realización de una prueba de concepto sobre un simulador.
>>> Enlace a la primera entrega de la serie.
Lógica combinatoria: los multiplexores
Un multiplexor es un circuito combinacional con varias entradas y una salida que permite, mediante una entrada adicional de selección, decidir qué entrada se enruta a la salida.
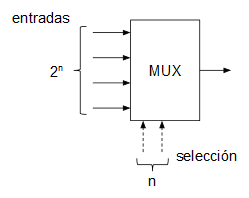
El código VHDL para un multiplexor de, por ejemplo, 3 entradas sería el siguiente:
library ieee; use ieee.std_logic_1164.all; entity Mux3Inputs is generic ( NBits : integer := 16 ); port ( Sel : in std_logic_vector(1 downto 0); DataIn0 : in std_logic_vector((NBits - 1) downto 0); DataIn1 : in std_logic_vector((NBits - 1) downto 0); DataIn2 : in std_logic_vector((NBits - 1) downto 0); DataOut : out std_logic_vector((NBits - 1) downto 0) ); end entity; architecture Architecture1 of Mux3Inputs is begin DataOut <= DataIn0 when (Sel = "00") else DataIn1 when (Sel = "01") else DataIn2; end architecture;
Lógica combinatoria: el expansor del signo
El expansor del signo (EXP) es un bloque combinacional que expande el signo de un valor de M bits a N bits siendo M < N.
En nuestro caso, el expansor del signo incluye una entrada de selección de un bit para elegir entre M=12 (instrucciones de salto relativo) y M=15 (sólo para la instrucción LOADI).
library ieee; use ieee.std_logic_1164.all; entity SignExp is generic ( NBitsToExpand0 : integer := 15; NBitsToExpand1 : integer := 12; NBits : integer := 16 ); port ( SelIn : in std_logic; DataIn : in std_logic_vector((NBits - 1) downto 0); DataOut : out std_logic_vector((NBits - 1) downto 0) ); end SignExp; architecture Architecture1 of SignExp is signal Expansion0 : std_logic_vector((NBits - NBitsToExpand0 - 1) downto 0); signal Expansion1 : std_logic_vector((NBits - NBitsToExpand1 - 1) downto 0); begin Expansion0 <= (others => DataIn(NBitsToExpand0 - 1)); Expansion1 <= (others => DataIn(NBitsToExpand1 - 1)); DataOut <= Expansion0 & DataIn((NBitsToExpand0 - 1) downto 0) when (SelIn = '0') else Expansion1 & DataIn((NBitsToExpand1 - 1) downto 0); end Architecture1;
Lógica combinatoria: ALU
La ALU es en este caso incluye dentro dos multiplexores, un sumador y un negador.
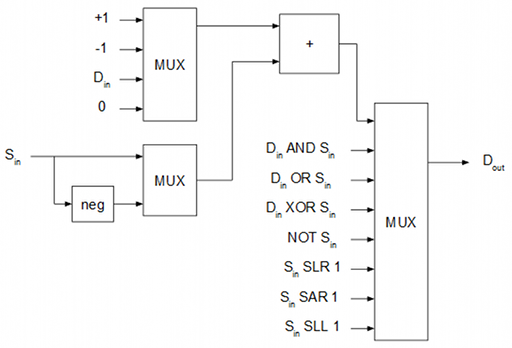
Partiendo de este diseño, la implementación en VHDL es directa.
library ieee; use ieee.std_logic_1164.all; use ieee.numeric_std.all; entity Alu is generic ( NBits : integer := 16 ); port ( DIn : in std_logic_vector((NBits - 1) downto 0); SIn : in std_logic_vector((NBits - 1) downto 0); RAIn : in std_logic_vector((NBits - 1) downto 0); DOut : out std_logic_vector((NBits - 1) downto 0); SelIn : in std_logic_vector(3 downto 0) ); end entity; architecture Architecture1 of Alu is component Adder is generic ( NBits : integer := 16 ); port ( A : in std_logic_vector((NBits - 1) downto 0); B : in std_logic_vector((NBits - 1) downto 0); Y : out std_logic_vector((NBits - 1) downto 0) ); end component; component Neg is generic ( NBits : integer := 16 ); port( DataIn : in std_logic_vector((NBits - 1) downto 0); DataOut : out std_logic_vector((NBits - 1) downto 0) ); end component; signal AddOut : std_logic_vector((NBits - 1) downto 0); signal SInNeg : std_logic_vector((NBits - 1) downto 0); signal FirstOperand : std_logic_vector((NBits - 1) downto 0); signal SMuxOut : std_logic_vector((NBits - 1) downto 0); begin -- mux for the first operand of the adder FirstOperand <= std_logic_vector(to_signed(1, NBits)) when (SelIn = "0111") else -- inc std_logic_vector(to_signed(-1, NBits)) when (SelIn = "1000") else -- dec DIn when ((SelIn = "0001") or (SelIn = "0010") or (SelIn = "1100") or (SelIn = "1101")) else -- add, sub, jz, jn (others => '0'); -- assign -- neg Y Negate : Neg generic map ( NBits => NBits ) port map ( DataIn => SIn, DataOut => SInNeg ); -- src mux SMuxOut <= SInNeg when (SelIn = "0010") else -- sub (others => '0') when ((SelIn = "1100") and (RAIn /= std_logic_vector(to_unsigned(0, NBits)))) or ((SelIn = "1101") and (RaIn(NBits - 1) = '0')) else -- jz, jn SIn; -- adder Add : Adder generic map ( NBits => NBits ) port map ( A => FirstOperand, B => SMuxOut, Y => AddOut ); -- final mux DOut <= AddOut when ((SelIn = "0000") or (SelIn = "0001") or (SelIn = "0010") or (SelIn = "0111") or (SelIn = "1000") or (SelIn = "1100") or (SelIn = "1101")) else (DIn and SIn) when (SelIn = "0011") else (DIn or SIn) when (SelIn = "0100") else (DIn xor SIn) when (SelIn = "0101") else (not(SIn)) when (SelIn = "0110") else ('0' & SIn(15 downto 1)) when (SelIn = "1001") else -- slr (SIn(15) & SIn(15 downto 1)) when (SelIn = "1010") else -- sar (SIn(14 downto 0) & '0') when (SelIn = "1011") else -- sll (others => '0'); end architecture;
Nótese que el componente “Neg” es el negador y calcula el complemento a dos (también se trata, a su vez, de un circuito combinacional)
Lógica secuencial: los registros
Un registro no es más que una colección de biestables D en paralelo, uno por cada bit.
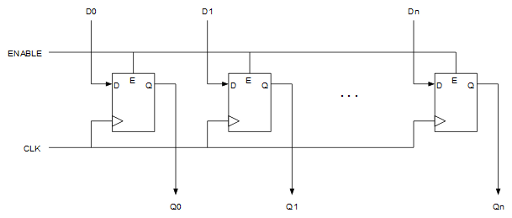
La forma más portable de implementar una entrada “enable” es poniendo un multiplexor en la entrada D que seleccione entre la entrada exterior y realimentar la propia Q. De esta forma simulamos un “enable” con lógica “estándar”.
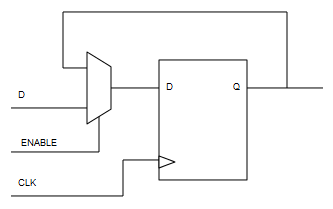
La implementación en VHDL de biestables D es directa:
library ieee; use ieee.std_logic_1164.all; entity Reg is generic ( NBits : integer := 16 ); port ( Enable : in std_logic; Clk : in std_logic; DataIn : in std_logic_vector((NBits - 1) downto 0); DataOut : out std_logic_vector((NBits - 1) downto 0) ); end Reg; architecture Architecture1 of Reg is signal QBus : std_logic_vector((NBits - 1) downto 0); signal DBus : std_logic_vector((NBits - 1) downto 0); signal PreDBus : std_logic_vector((NBits - 1) downto 0); begin process (Clk) begin if (Clk'event and (Clk = '1')) then QBus <= DBus; end if; end process; DBus <= PreDBus when (Enable = '1') else QBus; PreDBus <= DataIn; DataOut <= QBus; end Architecture1;
Lógica secuencial: la memoria
La unidad de memoria viene con una RAM y una ROM. Una memoria ROM no requiere secuencialidad y puede ser implementada como una LUT de forma combinatoria:
library ieee; use ieee.std_logic_1164.all; use ieee.numeric_std.all; entity Rom is port ( AddressIn : in std_logic_vector(12 downto 0); DataOut : out std_logic_vector(15 downto 0) ); end entity; architecture Architecture1 of Rom is type RomType is array (0 to 8191) of std_logic_vector(15 downto 0); constant Data : RomType := ( "0001000000000000", -- load "0010000000001000", -- op ra, ra, dec "0011000000000000", -- store others => "0000000000000000" ); begin DataOut <= Data(to_integer(unsigned(AddressIn))); end architecture;
La memoria RAM sí requiere de la señal de reloj ya que es un circuito secuencial. La implementación VHDL usada es la recomendada por la mayoría de los fabricantes (usando un array de std_logic_vector):
library ieee; use ieee.std_logic_1164.all; use ieee.numeric_std.all; entity Ram is generic ( GPOutAddress : integer := 4096 ); port ( AddressIn : in std_logic_vector(12 downto 0); DataOut : out std_logic_vector(15 downto 0); DataIn : in std_logic_vector(15 downto 0); WriteEnable : in std_logic; GPOut : out std_logic_vector(15 downto 0); Clk : in std_logic ); end entity; architecture Architecture1 of Ram is type RamType is array(0 to 8191) of std_logic_vector(15 downto 0); signal Data : RamType; begin process (Clk) begin if ((Clk'event) and (Clk = '1')) then if (WriteEnable = '1') then Data(to_integer(unsigned(AddressIn))) <= DataIn; end if; end if; end process; DataOut <= Data(to_integer(unsigned(AddressIn))); GPOut <= Data(GPOutAddress); end architecture;
La RAM incluye un puerto “GPOut” que mapea la dirección de memoria 4096 de la RAM en un puerto de salida de 16 bits. Este añadido se usará más adelante, en la prueba de concepto, para facilitar la depuración del procesador.
La unidad de control
Como se vio en la primera entrega, la unidad de control es realmente una FSM (máquina de estados finita) cuyas salidas gobiernan las entradas “enable” de los registros, las entradas de selección de los multiplexores y el resto de la lógica del procesador.
La FSM de la unidad de control va avanzando el contador de programa, carga las instrucciones en el IR y ejecuta el microcódigo de cada instrucción. Los estados de la FSM comunes a cualquier instrucción que se ejecute son los siguientes (extraído del anterior post):
0. MUX6 := "0", Habilitar PC
1. MUX1 = PC, Habilitar ADDR
2. Habilitar DATAin
3. Habilitar IR
4. MUX5 := FSM, ALU := inc, MUX4 := PC, Habilitar PC
5. EJECUTAR EL MICROCÓDIGO DE LA INSTRUCCIÓN ALMACENADA EN IR
6. Ir al estado 1
A continuación puede verse el grafo completo de la FSM.
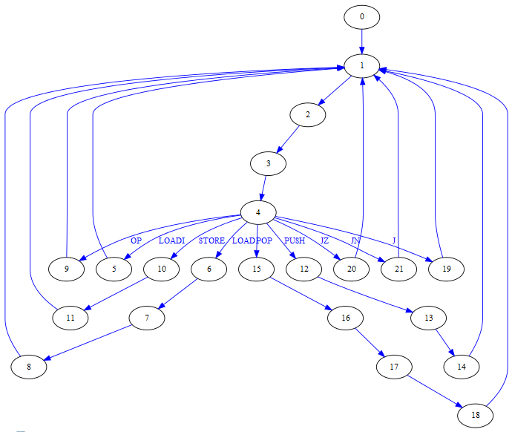
El estado 0 es al estado que se va en el reset. A continuación pueden verse también las señales que unen la unidad de control con el resto de la lógica del procesador:

Se ha optado por implementar la FSM como una máquina de tipo Moore (la salida depende sólo del estado actual y el estado siguiente depende de las entradas y del estado actual)
library ieee; use ieee.std_logic_1164.all; entity FSM is port ( DataOutEnable : out std_logic; DataInEnable : out std_logic; RAEnable : out std_logic; RBEnable : out std_logic; RCEnable : out std_logic; SPEnable : out std_logic; PCEnable : out std_logic; AddrEnable : out std_logic; IREnable : out std_logic; Mux1Sel : out std_logic_vector(1 downto 0); Mux2Sel : out std_logic_vector(1 downto 0); Mux3Sel : out std_logic_vector(2 downto 0); Mux4Sel : out std_logic_vector(2 downto 0); Mux5Sel : out std_logic; Mux6Sel : out std_logic; AluOpSel : out std_logic_vector(3 downto 0); MemWriteEnable : out std_logic; SignExpSel : out std_logic; IRValue : in std_logic_vector(15 downto 0); Clk : in std_logic; Reset : in std_logic ); end entity; architecture Architecture1 of FSM is signal QBus : std_logic_vector(4 downto 0); signal DBus : std_logic_vector(4 downto 0); begin process (Clk, Reset) begin if (Clk'event and (Clk = '1')) then if (Reset = '1') then QBus <= (others => '0'); else QBus <= DBus; end if; end if; end process; -- next state logic -- for state "00000" MUX6 := "0", Enable PC DBus <= "00001" when ((QBus = "00000") or (QBus = "00101") or (QBus = "01000") or (QBus = "01001") or (QBus = "01011") or (QBus = "01110") or (QBus = "10010") or (QBus = "10011") or (QBus = "10100") or (QBus = "10101")) else -- MUX1 := PC, Enable ADDR "00010" when (QBus = "00001") else -- Enable DATAIN "00011" when (QBus = "00010") else -- Enable IR "00100" when (QBus = "00011") else -- MUX5 := FSM, ALU := inc, MUX4 := PC, Enable PC -- LOADI states "00101" when ((QBus = "00100") and (IRValue(15) = '1')) else -- MUX2 := EXP, SignSel := 15 bits, Enable RA -- LOAD states "00110" when ((QBus = "00100") and (IRValue(15 downto 12) = "0001")) else -- MUX1 := RB, Enable ADDR "00111" when (QBus = "00110") else -- Enable DATAIN "01000" when (QBus = "00111") else -- MUX2 := DATAIN, Enable RA -- OP states "01001" when ((QBus = "00100") and (IRValue(15 downto 12) = "0010")) else -- MUX2 := ALU, MUX3 := dst, MUX4 := src, MUX5 := IR(3..0), Enable dst -- STORE states "01010" when ((QBus = "00100") and (IRValue(15 downto 12) = "0011")) else -- MUX1 := RB, Enable ADDR, Enable DATAOUT "01011" when (QBus = "01010") else -- WE := 1 -- PUSH states "01100" when ((QBus = "00100") and (IRValue(15 downto 12) = "0100")) else -- MUX4 := SP, MUX5 := FSM, ALU := inc, Enable SP "01101" when (QBus = "01100") else -- MUX1 := SP, Enable ADDR, Enable DATAOUT "01110" when (QBus = "01101") else -- WE := 1 -- POP states "01111" when ((QBus = "00100") and (IRValue(15 downto 12) = "0101")) else -- MUX1 := SP, Enable ADDR "10000" when (QBus = "01111") else -- Enable DATAIN "10001" when (QBus = "10000") else -- Enable RA, MUX2 := DATAIN "10010" when (QBus = "10001") else -- MUX4 := SP, MUX5 := FSM, ALU := dec, Enable SP -- J states "10011" when ((QBus = "00100") and (IRValue(15 downto 12) = "0110")) else -- MUX4 := EXP, SignSel := 12 bits, MUX3 := PC, MUX5 := FSM, ALU := add, Enable PC -- JZ states "10100" when ((QBus = "00100") and (IRValue(15 downto 12) = "0111")) else -- MUX4 := EXP, SignSel := 12 bits, MUX3 := PC, MUX5 := FSM, ALU := add if RA=0, Enable PC -- JN states "10101" when ((QBus = "00100") and (IRValue(15 downto 12) = "0000")) else -- MUX4 := EXP, SignSel := 12 bits, MUX3 := PC, MUX5 := FSM, ALU := add if RA<0, Enable PC "00000"; -- output logic DataOutEnable <= '1' when (QBus = "01010") or (QBus = "01101") else '0'; DataInEnable <= '1' when (QBus = "00010") or (QBus = "00111") or (QBus = "10000") else '0'; RAEnable <= '1' when (QBus = "00101") or (QBus = "01000") or (QBus = "10001") or ((QBus = "01001") and (IRValue(10 downto 8) = "000")) else '0'; RBEnable <= '1' when (QBus = "01001") and (IRValue(10 downto 8) = "001") else '0'; RCEnable <= '1' when (QBus = "01001") and (IRValue(10 downto 8) = "010") else '0'; SPEnable <= '1' when (QBus = "01100") or (QBus = "10010") or ((QBus = "01001") and (IRValue(10 downto 8) = "011")) else '0'; PCEnable <= '1' when (QBus = "00000") or (QBus = "00100") or (QBus = "10011") or (QBus = "10100") or (QBus = "10101") or ((QBus = "01001") and (IRValue(10 downto 8) = "100")) else '0'; AddrEnable <= '1' when (QBus = "00001") or (QBus = "00110") or (QBus = "01010") or (QBus = "01101") or (QBus = "01111") else '0'; IREnable <= '1' when (QBus = "00011") else '0'; Mux1Sel <= "00" when (QBus = "00110") or (QBus = "01010") else "01" when (QBus = "01101") or (QBus = "01111") else "10"; Mux2Sel <= "00" when (QBus = "01000") or (QBus = "10001") else "01" when (QBus = "01001") else "10"; Mux3Sel <= "100" when (QBus = "10011") or (QBus = "10100") or (QBus = "10101") else IRValue(10 downto 8); Mux4Sel <= "011" when (QBus = "01100") or (QBus = "10010") else "100" when (QBus = "00100") else "101" when (QBus = "10011") or (QBus = "10100") or (QBus = "10101") else IRValue(6 downto 4); Mux5Sel <= '0' when (QBus = "01001") else '1'; Mux6Sel <= '0' when (QBus = "00000") else '1'; AluOpSel <= "0111" when (QBus = "00100") or (QBus = "01100") else "1000" when (QBus = "10010") else "0001" when (QBus = "10011") else "1100" when (QBus = "10100") else "1101" when (QBus = "10101") else "0000"; MemWriteEnable <= '1' when (QBus = "01011") or (QBus = "01110") else '0'; SignExpSel <= '0' when (QBus = "00101") else '1'; end architecture;
Al igual que en otras ocasiones, una vez tenemos el grafo de la FSM, su implementación en VHDL es totalmente mecánica.
Prueba de concepto
Como primera aproximación se ha creado un fichero Rom.vhd que contiene, escrito a mano, el código máquina del siguiente código ensamblador:
# GPOut := 10 loadi 12288 op rb, ra, assign loadi 10 store loop: # if (GPOut == 0) then goto loopEnd loadi 12288 op rb, ra, assign load jz loopEnd # decrementar GPOut loadi 12288 op rb, ra, assign load op ra, ra, dec store # bucle j loop loopEnd: j loopEnd
Para este programa el código VHDL de la ROM quedaría como sigue:
library ieee; use ieee.std_logic_1164.all; use ieee.numeric_std.all; entity Rom is port ( AddressIn : in std_logic_vector(12 downto 0); DataOut : out std_logic_vector(15 downto 0) ); end entity; architecture Architecture1 of Rom is type RomType is array (0 to 8191) of std_logic_vector(15 downto 0); constant Data : RomType := ( -- simple counter "1011000000000000", -- loadi 12288 "0010000100000000", -- op rb, ra, assign "1000000000001010", -- loadi 10 "0011000000000000", -- store -- loop: "1011000000000000", -- loadi 12288 "0010000100000000", -- op rb, ra, assign "0001000000000000", -- load "0111000000000110", -- jz loopEnd (+6) "1011000000000000", -- loadi 12288 "0010000100000000", -- op rb, ra, assign "0001000000000000", -- load "0010000000001000", -- op ra, ra, dec "0011000000000000", -- store "0110111111110110", -- j loop (-10) -- loopEnd: "0110111111111111", -- j loopEnd (-1) others => "0000000000000000" ); begin DataOut <= Data(to_integer(unsigned(AddressIn))); end architecture;
El puerto de salida está en la dirección 4096 de nuestra RAM pero como la RAM está situada después de la ROM, la dirección de memoria de este puerto de salida será realmente 8192 + 4096 = 12288.
Ejecutando la simulación
El paquete de software usado para realizar la simulación es el GHDL, un compilador y simulador VHDL open source que genera ficheros VCD de eventos. Estos ficheros VCD contienen las señales digitales de todo el circuito simulado y son visualizables con herramientas como el GtkWave.
El testbench utilizado se encarga simplemente de generar el tren de pulsos del reloj y de realizar un reset al principio.
Reset <= '0' after 3 ns; Finished <= '1' after 2 us; Clk <= not Clk after 1 ns when Finished /= '1' else '0';
A continuación pueden verse las señales de nuestra CPU al ejecutar una instrucción LOADI justo después del reset:
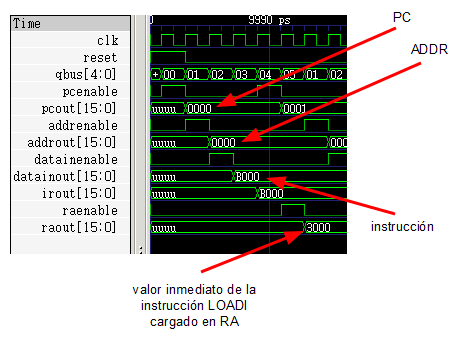
Si observamos el puerto de salida GPOut y alejamos el zoom se puede ver cómo el procesador ha ejecutado el programa correctamente (cuenta descendente desde 10 hasta 0 y se detiene).

Ya hemos conseguido que nuestro provesador V1 funcione en un simulador, ahora sólo nos queda implementarlo en una FPGA, pero eso será en la próxima entrega :-).
En la sección soft puede descargarse todo el código VHDL del proyecto.
>>> Enlace a la tercera entrega de la serie.
[ añadir comentario ] ( 2955 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 3791 )
( 3 / 3791 )
 Calendario
Calendario




