Introducción
Mi hijo recibió por su cumpleaños un despertador con temática Minecraft que le gustó mucho salvo por el sonido que tenía como despertador, que estaba prefijado y era una supuesta grabación "inspirada" en el juego.
Dicha grabación se escucha saturada y con poca calidad por lo que resulta desagradable de escuchar y mi hijo me pidió que intentara cambiarla.
En el siguiente vídeo grabado por un youtuber que hace reviews de este tipo de cosas puede escucharse el sonido original que trae este despertador (instante 4:50 aprox.).
Planteamiento del problema
Se parte de un reloj despertador con una circuitería muy cerrada y no documentada y el objetivo es cambiar el sonido que se escucha cuando suena la alarma, que, de fábrica, es un sonido pregrabado:
Las placas tienen escasa serigrafía y el único integrado visible está "borrado". Lo ideal sería obtener una señal digital que indique la activación de la alarma.
Investigación
El cable plano que une la placa principal con la placa de botones, leds y el chip de audio es un cable plano de 10 hilos que sólo tiene los dos extremos serigrafiados como "vdd" y "gnd".
Si a los 10 cables les quitamos los dos de alimentación de los extremos quedan 8 cables que no se sabe para qué son, sin embargo se intuye, dada la funcionalidad de esa placa, que esos 8 cables están distribuidos de la siguiente manera:
- 6 señales para leer los botones (el reloj tiene una cruceta de 4 botones más 2 botones adicionales).
- 1 señal para controlar los leds blancos (que se usan para la funcionalidad de lámpara).
- 1 señal para controlar la música (cuando suena la alarma).
Tras varias pruebas se verifica que la distribución de las señales es la siguiente.
Y que la señal "alarma" utiliza lógica positiva: se pone a 5 voltios para que suene la alarma y se pone a 0 voltios para apagar la alarma.
Desarrollo de la solución
Teniendo localizado el cable de la señal "alarma" el objetivo ahora es hacer un pequeño montaje que permita reproducir otro tipo de música o sonido en el despertador y para ello se plantea el siguiente esquema eléctrico:
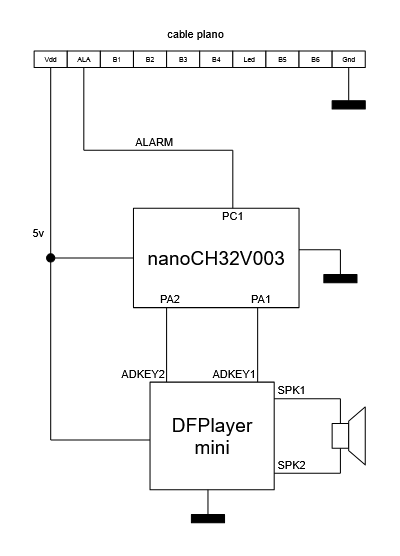
Toda la circuitería del reloj despertador y del DFPlayer Mini funciona con 5 voltios, pero el CH32V003 funciona con 3.3 voltios. En este caso se utiliza una placa "nanoCH32V003" para que pueda alimentarse a 5 voltios de la propia fuente del reloj despertador. El cable de alarma se conecta a PC1 o a cualquier otra entrada del CH32V003 siempre y cuando sea un pin tolerante a 5 voltios (no todos los pines de ese microcontrolador lo son).
El DFPlayer Mini es un módulo de reproducción de MP3 que incluye lector de tarjeta de memoria microSD. Dispone de dos pines dedicados (ADKEY1 y ADKEY2) que, cuando se ponen a masa reproducen, respectivamente, el primer y el quinto MP3 de la tarjeta de memoria. El módulo carece de pines para detener la reproducción pero, como en este caso sólo se precisa que hayan único sonido, se opta por una solución simple:
- Como 1er sonido de la tarjeta de memoria se pone el sonido que queremos que tenga el despertador.
- Como 5o sonido de la tarjeta de memoria se pone un MP3 de un segundo de silencio.
De esta forma poniendo ADKEY1=0 se reproduce el sonido nuevo y poniendo ADKEY2=0 "paramos" la reproducción al reproducir el MP3 de silencio.
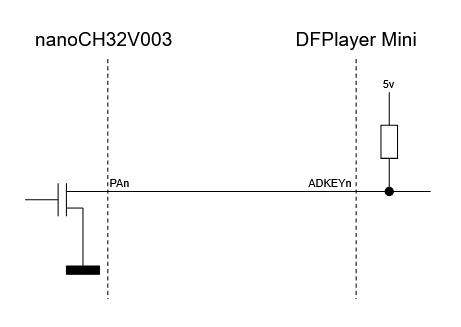
Se configuran las salidas PA1 y PA2 del microcontrolador como salidas en colector abierto (open drain): emitiendo un 1 se ponen en alta impedancia y emitiendo un 0 se ponen a masa, que es el comportamiento que se quiere para controlar el DFPlayer Mini:
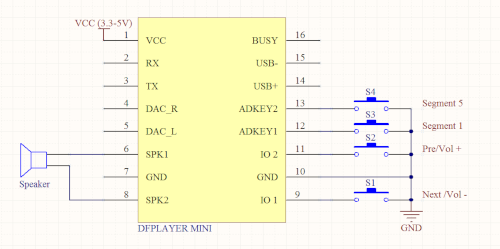
(imagen extraída de www.prometec.net)
PA1 y PA2 se configuran en open-drain debido a dos razones:
- El DFPlayer Mini ya dispone de resistencias pull-up en las entradas ADKEY1 y ADKEY2.
- El DFPlayer Mini está alimentado a 5 voltios mientras que el CH32V003 lo está a 3.3 voltios, por lo que un "1" del CH32V003 no sería igual que un "1" para el DFPlayer Mini. Usando salidas en open-drain nos aseguramos de que la corriente que circula por los cables PA1 y PA2 proviene del DFPlayer Mini (5 voltios), no del CH32V003 (3.3 voltios).
Código
El código del microcontrolador CH32V003 será el encargado de muestrear el cable "alarm" a intervalos regulares (cada 100 milisegundos). Cuando el cable "alarm" se ponga a 1 el microcontrolador pondrá a 0 (masa) durante un tiempo prefijado la salida conectada a ADKEY1 y cuando el cable "alarm" pase de nuevo a 0, el microcontrolador pondrá el pin conectado a ADKEY2 a 0 (masa) también durante un tiempo prefijado (el correspondiente a reproducir un silencio). La máquina de estados tendrá, por tanto una entrada (la señal del cable "alarm") y dos salidas (que gobiernan las salidas en colector abierto de ADKEY1 y ADKEY2).
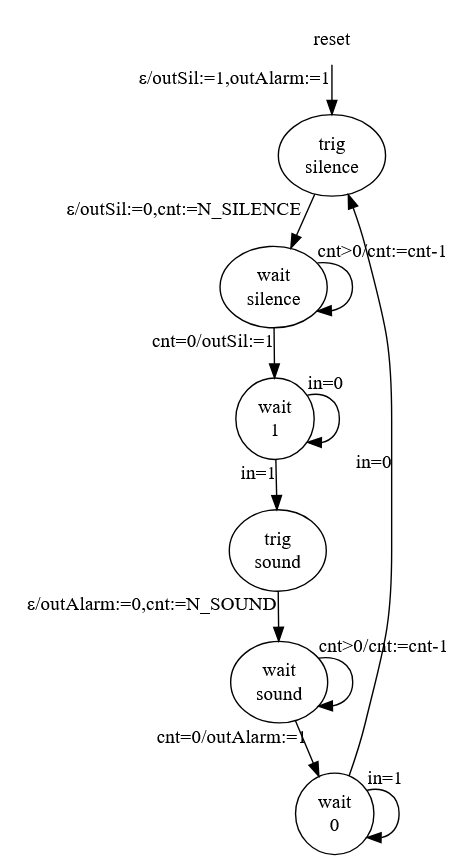
El reloj de esta máquina de estados viene dado por el timer del microcontrolador, que tiene un período de 100 milisegundos:
- N_SILENCE es la cantidad de ticks de reloj que debe permanecer a masa la salida "silencio".
- N_SOUND es la cantidad de ticks de reloj que debe permanecer a masa la salida "sonido".
La cantidad total de milisegundos que se ponga a masa cada salida será de N_SILENCE * 100 y de N_SOUND * 100 milisegundos respectivamente.
void AlarmControl::run() { Status localStatus = this->status; do { this->status = localStatus; if (localStatus == Status::RESET) { this->io.stopTrigSound(); this->io.stopTrigSilence(); localStatus = Status::TRIG_SILENCE; } else if (localStatus == Status::TRIG_SILENCE) { this->io.startTrigSilence(); this->counter = N_SILENCE; localStatus = Status::WAIT_SILENCE; } else if (localStatus == Status::WAIT_SILENCE) { this->counter--; if (this->counter == 0) { this->io.stopTrigSilence(); localStatus = Status::WAIT_1; } } else if (localStatus == Status::WAIT_1) { if (this->io.getAlarm()) localStatus = Status::TRIG_SOUND; } else if (localStatus == Status::TRIG_SOUND) { this->io.startTrigSound(); this->counter = N_SOUND; localStatus = Status::WAIT_SOUND; } else if (localStatus == Status::WAIT_SOUND) { this->counter--; if (this->counter == 0) { this->io.stopTrigSound(); localStatus = Status::WAIT_0; } } else if (localStatus == Status::WAIT_0) { if (!this->io.getAlarm()) localStatus = Status::TRIG_SILENCE; } } while (localStatus != this->status); }
La máquina de estados se implementa en la clase "AlarmControl" que decibe en su construcción una referencia a un objeto que debe heredar de "AlarmControlIO".
class AlarmControlIO { public: virtual bool getAlarm() = 0; virtual void startTrigSound() = 0; virtual void stopTrigSound() = 0; virtual void startTrigSilence() = 0; virtual void stopTrigSilence() = 0; }; class AlarmControl { protected: AlarmControlIO &io; enum class Status { RESET, TRIG_SILENCE, WAIT_SILENCE, WAIT_1, TRIG_SOUND, WAIT_SOUND, WAIT_0 }; Status status; uint32_t counter; static const uint32_t N_SILENCE = 4; static const uint32_t N_SOUND = 4; public: AlarmControl(AlarmControlIO &alarmControlIO) : io(alarmControlIO), status(Status::RESET) { }; void run(); };
En el fichero "main.cc" se define una clase "MyListener" que tiene un objeto de tipo "AlarmControl" como propiedad y que hereda de:
- "TimerListener" (lo que la obliga a incluir la función miembro "timerExpired()" que se ejecutará cada vez que se desborde el contador de SysTick cada 100 milisegundos).
- "AlarmControlIO" (lo que la obliga a incluir las funciones miembro "bool getAlarm()" para leer el estado de la señal "Alarm" y las otras cuatro funciones "void startTrigSound()", "void stopTrigSound()", "void startTrigSilence()" y "void stopTrigSilence()" para controlar los pines PA1 y PA2 que son los que gobiernan el reproductor MP3 DFPlayer Mini).
En la función miembro "timerExpired()" se invoca, a su vez, a la función miembro "run()" del objeto "AlarmControl" para que se vaya iterando la máquina de estados cada 100 milisegundos.
void MyListener::timerExpired() { this->alarmControl.run(); } bool MyListener::getAlarm() { return (GPIOC_INDR & (((uint32_t) 1) << 1)) ? true : false; // read PC1 } void MyListener::startTrigSound() { GPIOA_OUTDR &= ~(((uint32_t) 1) << 1); // PA1 = 0 } void MyListener::stopTrigSound() { GPIOA_OUTDR |= (((uint32_t) 1) << 1); // PA1 = high z } void MyListener::startTrigSilence() { GPIOA_OUTDR &= ~(((uint32_t) 1) << 2); // PA2 = 0 } void MyListener::stopTrigSilence() { GPIOA_OUTDR |= (((uint32_t) 1) << 2); // PA2 = high z } int main() { interruptInit(); MyListener myListener; Timer::init(myListener, 100_msForTimer); while (true) asm volatile ("wfi"); }
En la función "main()" simplemente se declara un objeto de tipo "MyListener" (la construcción de este objeto también incluye la construcción del objeto "AlarmControl" debido a que es una propiedad del primero), se inicializa el Timer y nos quedamos en bucle infinito de "wfi" (para consumir poca energía entre tick y tick de la máquina de estados).
Consideraciones particulares entorno al microcontrolador CH32V003
El CH32V003 es un RISC-V muy barato y muy limitado, al contrario que el GD32VF103 que se ha utilizado hasta ahora para otros proyectos con microcontrolador, el CH32V003 tiene las siguientes características:
- 16 Kb de memoria flash para programa.
- 2 Kb de memoria SRAM.
- El controlador de interrupciones no es el estándar CLIC, sino un controlador propietario (llamado PFIC) que se encuentra documentado en el manual de referencia del microcontrolador.
- El núcleo es un "QingKeV2", un RISC-V de perfil RV32EC. E = Embedded (16 registros de propósito general en lugar de los 32 del perfil RV32I) y C = Compressed (acepta instrucciones comprimidas de 16 bits, una especie de equivalente al modo "thumb" de los Cortex-M de ARM).
- Un "SysTick" integrado en el núcleo parecido al que tienen los Cortex-M de ARM.
En la sección soft hay disponible un pequeño proyecto de blinker (ch32v003-pfic-blinker) que utiliza el controlador de interrupciones de este microcontrolador junto con ese "systick" para hacer parpadear un led. Nótese los flags que se pasan al compilador:
-march=rv32eczicsr -mabi=ilp32e
Y la forma en que se habilitan las interrupciones en "interrupt.cc", que son diferentes a como se hace en el GD32VF103.
Tostar el microcontrolador
Para tostar el microcontrolador la mejor opción es pillar un programador WCH-LinkE del propio fabricante (es muy barato, a mi me costó menos de 10 ¤) ya que el protocolo de depuración y tostado es propietario del fabricante (aunque está totalmente documentado y hay proyectos en curso para no depender de ese programador hardware en particular).
El software para acceder al WCH-LinkE que utilicé es el programa "minichlink" (un sub proyecto dentro del repositorio https://github.com/cnlohr/ch32v003fun). Basta con hacer "make" en la carpeta "minichlink" dentro de ese repositorio y se genera el ejecutable "minichlink" que nos permite tostar el CH32V003:
./minichlink -w /ruta/al/main.bin 0x08000000
Montaje y resultados finales
A continuación puede verse cómo se realizaron las conexiones al conector del cable plano para extraer los 5 voltios, masa y la señal de alarma.
Cómo se realizó el montaje del prototipo con el microcontrolador y el DFPlayer Mini en una protoboard externa.
Y el paso del circuito de la protoboard a la PCB que se alojará dentro del reloj despertador:
A continuación un vídeo de demostración con el nuevo sonido (que ya no es la música de Minecraft).
El sonido que se ha puesto como sonido de alarma es el típico de los despertadores de toda la vida (que era el que quería mi hijo) y se ha descargado de https://pixabay.com/sound-effects/031974-30-seconds-alarm-72117/ (Pixabay permite uso libre de los sonidos que se descarguen de su web mientras no se revendan).
Todo el código en la seción soft.
[ añadir comentario ] ( 151 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |
( 2.7 / 100 )En esta cuarta entrega de esta miniserie sobre el desarrollo de la GabrielBoy, se abordará el diseño y desarrollo del tercero de los juegos incluidos: un snake, al más puro estilo de los que incluían los antiguos móviles Nokia.
Mecánica del juego
Tenemos una cuadrícula de 30x30 posiciones por la que va deambulando una serpiente que tenemos que dirigir en pos de su comida (la comida va apareciendo aleatoriamente por el tablero). Cada vez que la serpiente come una pieza crece una unidad en tamaño y el jugador debe evitar chocarse tanto contra los bordes del tablero como contra él mismo (a medida que la serpiente crece se hace más complicado evitar chocarnos contra nosotros mismos).
Es un juego muy conocido por antiguos propietarios de móviles de la marca Nokia, ya que esteos terminales los solían traer de serie, además, el juego no tiene fin en el sentido de que nunca "se gana", simplemente hay que tratar de sobrevivir lo máximo posible sin chocarnos contra los bordes o contra nosotros mismos a medida que comemos y crecemos en longitud.
Diseño de la pantalla
La única pantalla que tiene el juego está gestionada por la clase "SnakeMainScreen" (en la carpeta "games/snake"). Consiste en un tablero central, que alberga 30 x 30 huecos de 2 x 2 pixels cada uno. Con estas dimensiones tenemos un tablero que ocupa 60 x 60 pixels y que se coloca en el centro de la pantalla. A este tablero se le añade un borde de 2 pixels de anchura en todo su perímetro, por lo que al final tenemos que el tablero ocupa un total de 64x64 pixels. Los huecos de los lados son de 32 pixels a izquierda (donde se coloca un dibujo estático) y de 32 pixels a la derecha (donde va el contador de frutas comidas "fru").
Desarrollo
Cada posición del tablero de 30x30 es un byte que podrá tener uno de los siguientes valores:
- 0: para indicar que esta posición está vacía.
- SnakeDirection::TO_UP: para indicar que hay serpiente en esta posición y que el siguiente punto de la serpiente (en dirección a su cabeza) está en la posición de arriba.
- SnakeDirection::TO_DOWN: igual pero indicando que el siguiente punto de la serpiente (en dirección a su cabeza) está en la posición de abajo.
- SnakeDirection::TO_LEFT: ídem hacia la izquierda.
- SnakeDirection::TO_RIGHT: ídem hacia la derecha.
- FOOD: para indicar que en esa posición hay una pieza de comida.
Aparte de estos datos en el tablero, se mantienen las coordenadas de la cabeza y de la cola de la serpiente y no es necesario almacenar su longitud. Esta forma de modelar la serpiente en el tablero nos permite simplificar tanto el movimiento como el crecimiento de la misma:
- Para movernos basta con hacer avanzar la cabeza en la dirección actual o la indicada por la última pulsación de los botones de dirección, y la cola en la dirección que indique la propia celda del tablero (recordemos que los valores SnakeDirection::TO_XXXX indican el siguiente elemento de la serpiente en dirección a su cabeza).
- Cada vez que la serpiente come (la cabeza se encuentra con comida) lo único diferente que se hace es que la cola NO avance, por lo que, de forma efectiva, estamos haciendo crecer la serpiente.
Como se puede ver, no es necesario guardar ni controlar el tamaño de la serpiente puesto que la cola siempre es capaz de "encontrar su camino" (aunque se realicen zigzags en bloque y en celdas adyacentes del tablero).
A continuación el código de la función miembro "SnakeMainScreen::advance", que es la encargada de gestionar el avance de la serpiente. Como se puede ver en el código en caso de que la cabeza de la serpiente se encuentre con comida la única diferencia es que la cola no avanza.
void SnakeMainScreen::advance(Collide &c) { c = Collide::NO; // check direction int16_t newHeadX = this->headX + this->dir->x; int16_t newHeadY = this->headY + this->dir->y; if ((newHeadX < 0) || (newHeadX >= BOARD_WIDTH) || (newHeadY < 0) || (newHeadX >= BOARD_HEIGHT)) c = Collide::YES; else { // no collision to borders uint16_t oldHeadOffset = (this->headY * BOARD_WIDTH) + this->headX; uint8_t oldHeadValue = this->board[oldHeadOffset]; uint16_t newHeadOffset = (newHeadY * BOARD_WIDTH) + newHeadX; uint8_t newHeadValue = this->board[newHeadOffset]; if ((newHeadValue == SnakeDirection::TO_UP) || (newHeadValue == SnakeDirection::TO_DOWN) || (newHeadValue == SnakeDirection::TO_LEFT) || (newHeadValue == SnakeDirection::TO_RIGHT)) c = Collide::YES; else if (newHeadValue == 0) { uint16_t tailOffset = (this->tailY * BOARD_WIDTH) + this->tailX; uint8_t tailValue = this->board[tailOffset]; int16_t newTailX, newTailY; this->calculateNewTail(tailValue, newTailX, newTailY); this->board[tailOffset] = 0; this->drawBoardPosition(this->tailX, this->tailY, 0); this->tailX = newTailX; this->tailY = newTailY; } else if (newHeadValue == FOOD) { int16_t foodX, foodY; this->allocateNewFood(foodX, foodY); this->drawBoardPosition(foodX, foodY, 1); this->fruitCounter++; this->display.drawNumber(100, 32, this->fruitCounter, 3, Display::ShowZeros::YES); } this->board[oldHeadOffset] = this->dir->to; this->board[newHeadOffset] = this->dir->to; this->drawBoardPosition(newHeadX, newHeadY, 1); this->display.notifyFrameBufferChanged(); this->headX = newHeadX; this->headY = newHeadY; } }
Conclusiones y cierre de la serie
La consola GabrielBoy ha sido una primera aproximación al problema de implementar una consola portátil desde cero. La parte software es la parte que menos me ha costado ya que es un mundo al que estoy muy acostumbrado, mientras que la parte más compleja para mi ha sido planificar el espacio, hacer prototipos, las soldaduras, los diseño y la impresión 3D de la caja, etc.
Quiero dar las gracias a Aristóbulo, por su paciencia a la hora de enseñarme a usar el FreeCAD y por ayudarme en el diseño y la impresión de la caja de la consola.
Todo el código fuente y los diseños están disponibles en la sección soft.
[ añadir comentario ] ( 2567 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |
( 2.8 / 399 )En esta tercera entrenga de esta miniserie sobre el desarrollo de la GabrielBoy, se abordará el diseño y desarrollo del segundo juego: un shooter en 3D. Consiste en un entorno 3D simulado utilizando técnicas de raycasting en el que somos un tirador que debe recorrer el escenario y disparar a todos los items para pasar de nivel. Por limitaciones propias del hardware los muros en el juego son negros (se pintan los bordes pero no se rellenan), mientras que los items o "enemigos" son blancos (pixels rellenos) y fijos (no se mueven).
Mecánica del juego
Se trata de shooter 3D simplificado: hay que buscar todos los items blancos y dispararles con A para que desaparezcan. En el momento que hemos terminado con todos los items de un nivel, nos vamos al siguiente nivel, y así sucesivamente. En el juego no puedes "morir" simplemente vas cambiado de niveles y cuando terminas el último vuelves a empezar.
Diseño de la pantalla
La única pantalla que tiene el juego está gestionada por la clase TanksMainScreen (en la carpeta games/tanksfp). El dibujado de la escena 3D se realiza en el centro de la pantalla (64x64 pixels). Las zonas de los lados se utilizan para indicar cuantos items o enemigos quedan por abatir en el nivel actual y el número del nivel.
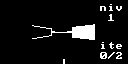
Renderizado de la escena usando raycasting
La técnica del raycasting, la utilizada en muchos de los juegos 3D de los años 90 y principios de los 2000 para dibujar escenas en 3D, se basaba realmente en el cálculo de colisiones de vectores bidimensionales. Para cada columna de la pantalla se calcula un vector 2D (rayo) que va desde el jugador hasta la escena pasando por ese punto de la pantalla.
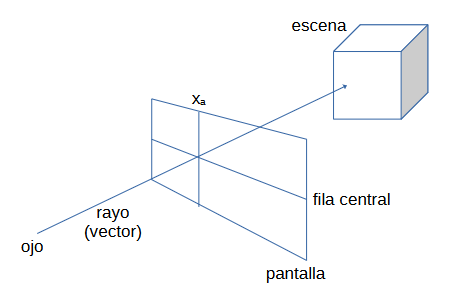
Si el vector choca con algún muro u objeto, se calcula la distancia a la que choca dicho vector y, por semejanza de triángulos con respecto a la altura del muro u objeto contra el que ha chocado el rayo, se calcula la altura que debe tener esa sección del objeto en la coordenada x por la que ha pasado el rayo.
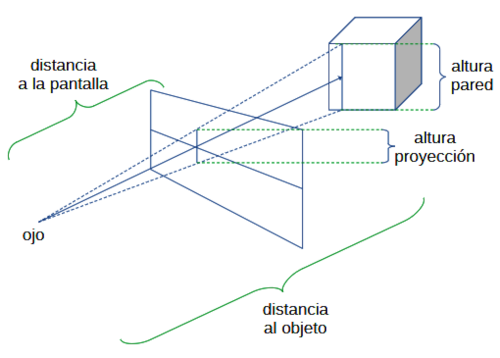
En este caso:
$$\frac{altura\ proyección}{distancia\ a\ la\ pantalla} = \frac{altura\ objeto}{distancia\ al\ objeto}$$
Se define un mundo en dos dimensiones en el que los muros y los items son segmentos y el jugador se mueve en el plano 2D:
const Level TanksMainScreen::LEVELS[] = { { // nivel 0 /* +---+ cada | | es un cuadrado de 10x10 unidades del mundo, P es el jugador +---+ +---+---+---+---+---+---+---+---+ | | + P--> + + | | | + +---+---+---+ | | +---+---+---+---+ + | | | + + + | | | + + + | | +---+---+---+---+---+---+---+---+ */ 80, // width = 80 (integer) 60, // height = 60 (integer) 8, // 8 segments { {{0, 0}, {5242880, 0}}, // scene segments (Q16.16 fixed point) {{5242880, 0}, {5242880, 3932160}}, {{5242880, 3932160}, {0, 3932160}}, {{0, 3932160}, {0, 0}}, {{0, 1966080}, {2621440, 1966080}}, {{2621440, 1966080}, {2621440, 3276800}}, {{3276800, 655360}, {3276800, 1310720}}, {{3276800, 1310720}, {5242880, 1310720}} }, {655360, 655360}, // (10, 10) (Q16.16 fixed point) 0, // player at (10, 10) looking with ANGLE[0] 2 // 2 collectable/shootable items }, // ... other levels };
El algoritmo de pintado “lanza” los 64 rayos correspondientes las 64 columnas de la ventana de la escena 3D (el recuadro de 64x64 pixels que se dibuja en el centro del display LCD) y para cada rayo, se calcula la intersección del mismo con cada uno de los segmentos del mundo y los enemigos (del nivel).
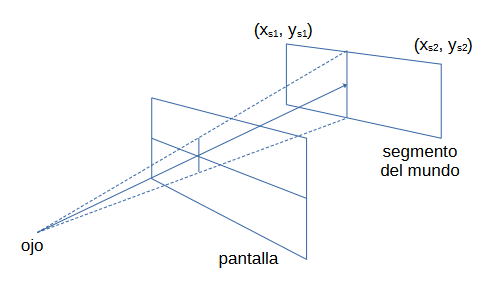
Cada segmento del mundo tendrá dos coordenadas 2D asociadas, mientras que cada rayo estará compuesto por la coordenada del jugador más un vector director unitario apuntando a la columna del display correspondiente. En cada frame, las coordenadas del jugador no cambian, lo que cambia es el vector director (el rayo).
El algoritmo grosso modo sería el siguiente:
para cada coordenada x entre -31 y +31 (se asume que 0 es el centro de la pantalla)
rayo = vector unitario que va desde el jugador y apunta a la columna x
distanciaColision = infinita
segmentoAPintar = ninguno
para cada segmento s del nivel
calcular las posible colisión entre el rayo y s
si colisiona y (distancia < distanciaColision) entonces
distanciaColision = distancia
segmentoAPintar = s
fin si
fin para
si (segmentoAPintar != ninguno) entonces
alturaEnPantalla = ALTURA * distanciaAPantalla / distanciaColision
pintar en la columna x un segmento vertical de tamaño alturaEnPantalla
en caso contrario
pintar en la columna x un punto en el centro (horizonte)
fin si
fin para
Cálculo de las colisiones
Cada segmento $s$ del mundo tendrá dos coordenadas 2D asociadas:
$$
\left( \left( x_{s1}, y_{s1} \right), \left( x_{s2}, y_{s2} \right) \right)
$$
Mientras que cada uno de los 64 rayos que se "lanzan" será un vector de la forma
$\left( \left( x_r , y_r \right), \left( x_{rd} , y_{rd} \right) \right)$ siendo $\left( x_r , y_r \right)$ las coordenadas del jugador en el mapa y $\left( x_{rd} , y_{rd} \right)$ el vector director unitario que apunta hacia el pixel.
Si definimos los puntos del segmento usando ecuaciones paramétricas, tenemos que:
$$
x = x_{s1} + t \left( x_{s2} - x_{s1} \right)\\
y = y_{s1} + t \left( y_{s2} - y_{s1} \right)
$$
Siendo $0 \leq t \leq 1$, de tal manera que:
$$
t = 0 \Rightarrow \left( x, y \right) = \left( x_{s1}, y_{s1} \right)\\
t = 1 \Rightarrow \left( x, y \right) = \left( x_{s2}, y_{s2} \right)
$$
Mientras que si definimos los puntos a lo largo del rayo que trazamos desde el jugador hasta la columna de la pantalla tenemos que:
$$
x = x_{r} + u x_{rd}\\
y = y_{r} + u y_{rd}
$$
Siendo $0 \le u$ y $u$ la distancia desde el jugador hasta $\left( x, y \right)$. A continuación definimos $d_{xs} = x_{s2} - x_{s1}$ y $d_{ys} = y_{s2} - y_{s1}$ y despejamos:
$$
x = x_{s1} + t d_{xs} = x_{r} + u x_{rd}\\
y = y_{s1} + t d_{ys} = y_{r} + u y_{rd}\\
t = \frac{x_{r} + u x_{rd} - x_{s1}}{d_{xs}}\\
u = \frac{y_{s1} + t d_{ys} - y_{r}}{y_{rd}}
$$
Por tanto:
$$
u = \frac{y_{s1} + \frac{x_{r} + u x_{rd} - x_{s1}}{d_{xs}} d_{fs} - y_{r}}{y_{rd}}\\
u y_{rd} = y_{s1} + \frac{x_{r} d_{ys}}{d_{xs}} + u \frac{x_{rd} d_{ys}}{d_{xs}} - \frac{x_{s1} d_{ys}}{d_{xs}} - y_{r}\\
u y_{rd} - u \frac{x_{rd} d_{ys}}{d_{xs}} = y_{s1} + \frac{x_{r} d_{ys}}{d_{xs}} - \frac{x_{s1} d_{ys}}{d_{xs}} - y_{r}\\
u \left( y_{rd} - \frac{x_{rd} d_{ys}}{d_{xs}} \right) = y_{s1} + \frac{x_{r} d_{ys}}{d_{xs}} - \frac{x_{s1} d_{ys}}{d_{xs}} - y_{r}\\
u = \frac{y_{s1} + \frac{x_{r} d_{ys}}{d_{xs}} - \frac{x_{s1} d_{ys}}{d_{xs}} - y_{r}}{y_{rd} - \frac{x_{rd} d_{ys}}{d_{xs}}}
$$
Multiplicando numerador y denominador por $d_{xs}$:
$$
u = \frac{d_{xs} y_{s1} + x_{r} d_{ys} - x_{s1} d_{ys} - y_{r} d_{xs}}{y_{rd} d_{xs} - x_{rd} d_{ys}}
$$
De esta forma ya tenemos calculado $u$ que será la distancia entre el jugador y la recta que contiene el segmento $s$. si $u < 0$ significará que el segmento está detrás del jugador.
Ahora con $u$ calculado, podemos sustituir su valor en:
$$
t = \frac{x_{r} + u x_{rd} - x_{s1}}{d_{xs}}
$$
Lo que nos dará el valor de $t$. Si $t < 0$ o $t > 1$ significará que el rayo no corta con el segmento. Nótese que si $y_{rd} d_{xs} - x_{rd} d_{ys} = 0$ significará que el rayo y la recta que contiene el segmento no se cortan (son paralelos) y debe ser tenido en cuenta para evitar una división entre 0:
TanksMainScreen::Intersection TanksMainScreen::getIntersection(const Segment &seg, const Vector &ray, const fixedpoint_t minRayT, fixedpoint_t &segT, fixedpoint_t &rayT) { fixedpoint_t dxs = seg.p2.x - seg.p1.x; fixedpoint_t dys = seg.p2.y - seg.p1.y; if ((dxs != 0) || (dys != 0)) { fixedpoint_t denRayT = (ray.dir.y * dxs) - (ray.dir.x * dys); if (denRayT != 0) { rayT = ((dxs * seg.p1.y) + (ray.p.x * dys) - (seg.p1.x * dys) - (ray.p.y * dxs)) / denRayT; if (rayT >= minRayT) { if (dxs != 0) segT = (ray.p.x + (rayT * ray.dir.x) - seg.p1.x) / dxs; else segT = (ray.p.y + (rayT * ray.dir.y) - seg.p1.y) / dys; if ((segT >= 0) && (segT <= fixedpoint_t::get(1))) return Intersection::ONE_POINT; } } } return Intersection::NO_POINT; }
Optimizaciones y datos precalculados
Todos los cálculos de precisión decimal se realizan utilizando aritmética de punto fijo en formato Q16.16 (enteros de 32 bits con 16 bits para la parte entera y 16 bits para la parte fraccionaria) y ayudándonos de la sobrecarga de operadores para facilitar la escritura de código y la mantenibilidad del mismo.
class fixedpoint_t { public: int32_t v; fixedpoint_t(int32_t x = 0) : v(x) { }; inline fixedpoint_t &operator = (const int32_t &x) { this->v = x << 16; return *this; }; inline fixedpoint_t operator + (const fixedpoint_t &x) const { fixedpoint_t ret; ret.v = this->v + x.v; return ret; }; inline fixedpoint_t operator - (const fixedpoint_t &x) const { fixedpoint_t ret; ret.v = this->v - x.v; return ret; }; inline fixedpoint_t operator - () const { fixedpoint_t ret; ret.v = -(this->v); return ret; }; inline fixedpoint_t operator * (const fixedpoint_t &x) const { fixedpoint_t ret; ret.v = (((int64_t) this->v) * ((int64_t) x.v)) >> 16; return ret; }; inline fixedpoint_t operator / (const fixedpoint_t &x) const { fixedpoint_t ret; ret.v = (((int64_t) this->v) << 16) / ((int64_t) x.v); return ret; }; inline bool operator == (const fixedpoint_t &x) const { return (this->v == x.v); }; inline bool operator != (const fixedpoint_t &x) const { return (this->v != x.v); }; inline bool operator < (const fixedpoint_t &x) const { return (this->v < x.v); }; inline bool operator > (const fixedpoint_t &x) const { return (this->v > x.v); }; inline bool operator <= (const fixedpoint_t &x) const { return (this->v <= x.v); }; inline bool operator >= (const fixedpoint_t &x) const { return (this->v >= x.v); }; inline fixedpoint_t operator += (const fixedpoint_t &x) { this->v += x.v; return *this; }; inline fixedpoint_t operator -= (const fixedpoint_t &x) { this->v -= x.v; return *this; }; inline int32_t getIntegerPart() { return this->v >> 16; }; inline static fixedpoint_t get(int32_t x) { fixedpoint_t ret; ret.v = x << 16; return ret; }; };
Además existen dos puntos clave en el código donde son necesarios cálculos trigonométricos:
1. El jugador está definido por sus coordenadas y por un vector unitario que apunta a "donde está mirando". Dicho vector coincide con el vector del rayo para la columna 0 de la pantalla por lo que cada rayo será una rotación del vector "hacia donde estoy mirando" y las rotaciones se deben calcular mediante senos y cosenos, así que lo que se hace en este caso es generar unas tablas precalculadas con los senos y los cosenos de los diferentes ángulos necesarios para calcular los 64 rayos de la pantalla. De hecho no hacen falta 64 senos y cosenos, basta con 32, puesto que la pantalla es simétrica.
2. Para que el jugador gire, se hace una rotación de su vector director alrededor de la coordenada del propio jugador y dicha rotación se realiza también aprovechando tablas precalculadas de senos y cosenos sólo para un cuadrante (son simétricos cambiándoles el signo para los otros tres cuadrantes de la circunferencia goniométrica).
Para ayudarnos en la generación de datos precalculados se hacen dos scripts:
- calculate_dir_vector.sh NUM_ÁNGULOS: Genera una tabla precalculada con los senos y los cosenos de NUM_ÁNGULOS en el intervalo $\left[ 0 , \frac{\pi}{2} \right)$. Los valores generador en formato de punto fijo Q16.16 (directamente "copiables y pegables" en el código C++).
- calculate_display_angles.sh DIST_TO_CENTER DISPLAY_WIDTH: Genera una tabla precalculada de 32 registros. Cada registro contiene un ángulo en radianes (no se usa en el código), el seno de ese ángulo, el coseno de ese ángulo y la distancia desde el jugador hasta el punto de la pantalla (el valor "distanciaAPantalla" necesario para calcular correctamente la altura de los objetos proyectados). DIST_TO_CENTER es la distancia desde el jugador hasta el centro de la pantalla en unidades del mundo y DISPLAY_WIDTH es la anchura de la pantalla en unidades del mundo.
A continuación se puede ver cómo queda el código que calcula el trazado de rayos de la pantalla a partir del vector del jugador:
const AngleAndDistance TanksMainScreen::DISPLAY_ANGLES_AND_DISTANCES[32] = { // precalculated vector of angles and distances to display from player // DISPLAY_ANGLES_AND_DISTANCES(i).angle = the angle in radians from center os display of pixel located at center +/- i (not used in code) // DISPLAY_ANGLES_AND_DISTANCES(i).cosineAngle = cos(angle) // DISPLAY_ANGLES_AND_DISTANCES(i).sineAngle = sin(angle) // DISPLAY_ANGLES_AND_DISTANCES(i).distance = the distance in world units from player to the pixel in the display located at center +/- i {0, 65536, 0, 327680}, // ./calculate_display_angles.sh 5 15 distance from player to center of display = 5 world units, display width = 15 world units {3069, 65464, 3068, 328039}, {6126, 65249, 6117, 329116}, {9155, 64897, 9126, 330904}, {12146, 64413, 12077, 333390}, {15087, 63806, 14954, 336559}, {17967, 63088, 17743, 340393}, {20778, 62269, 20432, 344869}, {23512, 61363, 23011, 349962}, {26163, 60382, 25473, 355646}, {28726, 59340, 27815, 361893}, {31199, 58248, 30034, 368675}, {33579, 57119, 32129, 375962}, {35866, 55963, 34102, 383726}, {38060, 54791, 35956, 391939}, {40161, 53610, 37694, 400572}, {42172, 52428, 39321, 409600}, {44094, 51253, 40842, 418996}, {45931, 50088, 42262, 428736}, {47684, 48940, 43587, 438799}, {49358, 47810, 44822, 449161}, {50955, 46704, 45974, 459803}, {52480, 45622, 47048, 470705}, {53934, 44567, 48049, 481851}, {55322, 43539, 48982, 493223}, {56647, 42540, 49852, 504807}, {57912, 41570, 50664, 516587}, {59120, 40629, 51421, 528551}, {60274, 39717, 52129, 540687}, {61378, 38834, 52790, 552983}, {62433, 37979, 53408, 565429}, {63442, 37152, 53987, 578016} }; ... void TanksMainScreen::calculateRay(Vector &ray, fixedpoint_t &distToDisplay, int32_t x) { // x = -31..31 ray = this->player; fixedpoint_t cosine = 1; fixedpoint_t sine = 0; if (x < 0) { cosine = DISPLAY_ANGLES_AND_DISTANCES[-x].cosineAngle; sine = DISPLAY_ANGLES_AND_DISTANCES[-x].sineAngle; distToDisplay = DISPLAY_ANGLES_AND_DISTANCES[-x].distance; } else { cosine = DISPLAY_ANGLES_AND_DISTANCES[x].cosineAngle; sine = -DISPLAY_ANGLES_AND_DISTANCES[x].sineAngle; distToDisplay = DISPLAY_ANGLES_AND_DISTANCES[x].distance; } ray.rotate(cosine, sine); }
Y cómo queda el código que calcula el cambio del vector del jugador cuando éste se gira:
const Angle TanksMainScreen::ANGLES[16] = { // 16 angles (cosines and sines) for first quadrant (other quadrant values are calculated changing cos/sin signs) {65536, 0}, // ./calculate_dir_vector.sh 16 {65220, 6423}, {64276, 12785}, {62714, 19024}, {60547, 25079}, {57797, 30893}, {54491, 36409}, {50660, 41575}, {46340, 46340}, {41575, 50660}, {36409, 54491}, {30893, 57797}, {25079, 60547}, {19024, 62714}, {12785, 64276}, {6423, 65220} }; ... void TanksMainScreen::fillAngle(Angle &a, const uint8_t i) { if (i < 16) a = ANGLES[ i ]; else if ((i >= 16) && (i < 32)) { a.cosine = -ANGLES[i - 16].sine; a.sine = ANGLES[i - 16].cosine; } else if ((i >= 32) && (i < 48)) { a.cosine = -ANGLES[i - 32].cosine; a.sine = -ANGLES[i - 32].sine; } else if (i >= 48) { a.cosine = ANGLES[i - 48].sine; a.sine = -ANGLES[i - 48].cosine; } } ... void TanksMainScreen::rotatePlayer(RotateTo t) { if (t == RotateTo::LEFT) this->playerAngle = (this->playerAngle + 1) & 0x3F; // 0..63 else if (t == RotateTo::RIGHT) this->playerAngle = (this->playerAngle + 64 - 1) & 0x3F; // 0..63 Angle a; fillAngle(a, this->playerAngle); this->player.dir.x = a.cosine; this->player.dir.y = a.sine; }
Conclusión y siguiente entrega
El uso de raycasting combinado con el cálculo mediante aritmética de punto fijo permite a un microcontrolador de potencia muy limitada proyectar escenas básicas en 3D en tiempo real y poder disfrutar de una experiencia 3D aunque sea en una pequeña pantalla LCD de 128x64 pixels. En la siguiente entrega de esta serie relacionada con la consola GabrielBoy se abordará el diseño y la implementación del mítico juego Snake.
Todo el código y los diseños están en la sección soft.
[ añadir comentario ] ( 316 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |
( 3.1 / 326 )En esta segunda entrega de esta miniserie sobre el desarrollo de la GabrielBoy, se abordará el diseño y desarrollo del primero de los juegos: un tetris. Se parte del diseño original del tetris, que consiste en una cuadrícula de 10x20 posiciones en la que van cayendo piezas que el jugador debe ir colocando buscando que llenen filas enteras. No me pararé en explicar el juego porque todos los conocemos. Así que vamos a ello.
Mecánica del juego
Se trata de un tetris estándar: van apareciendo las piezas por arriba de forma aleatoria, con la cruceta movemos a los lados o hacemos que la pieza baje más rápido y con el botón A rotamos la pieza. Cuando conseguimos hacer una o varias líneas horizontales completas dichas líneas de borran del tablero y aumenta la velocidad de caida en función de la cantidad de líneas eliminadas. El jugador nunca "gana", las fichas siguen cayendo indefinidamente hasta que apaguemos la consola, reiniciemos o la última ficha en caer ya no quepa en el tablero porque este está lleno.
Diseño de la pantalla
La única pantalla que tiene el juego está gestionada por la clase TetrisMainScreen (en la carpeta games/tetris). Dibuja un tablero central, que alberga 10 x 20 huecos de 3 x 3 pixels cada uno (cada “cuadrado” del tetris es un bloque de 3 x 3 pixels). Con estas dimensiones tenemos un tablero que ocupa 30 x 60 pixels y que se coloca en el centro de la pantalla. Los huecos de los lados son de 49 pixels a izquierda y de 49 pixels a la derecha (49 + 30 + 49 = 128 pixels de anchura de la pantalla LCD).
El hueco de la izquierda se utiliza para indicar la siguiente figura que va a caer mientras que el hueco de la derecha se utiliza para indicar el nivel por el que se va: cada 5 filas eliminadas se sube de nivel y aumenta un 5% la velocidad de caida de las figuras. El nivel máximo es el 9 y a partir de ese nivel ya no se aumenta la velocidad de caida.
Mecánica interna
El código no trabaja con el framebuffer de la pantalla, sino que trabaja con una matriz de 10 x 20 enteros en la que cada elemento puede tener los siguientes valores:
0: hueco libre.
1: hueco ocupado por suelo.
2: hueco ocupado por una pieza que está aún cayendo
static const int32_t BOARD_WIDTH = 10; static const int32_t BOARD_HEIGHT = 20; static const int32_t BOARD_SIZE = BOARD_WIDTH * BOARD_HEIGHT; uint8_t board[BOARD_SIZE] __attribute__ ((aligned(4)));
Se define el tablero con el atributo "aligned(4)" de GCC para garantizar que el compilador aloja dicha variable en una dirección de memoria múltiplo de 4 bytes (32 bits), de esta manera las operaciones de inicialización y rrecorrido del tablero puede optimizarse un poco más. Las figuras están definidas en un array constante (en ROM) de 7 elementos y cada elemento del array (cada figura) es una matriz de 4x4 bytes.
class TetrisFigure { public: static const int32_t MAX_WIDTH = 4; static const int32_t MAX_SIZE = MAX_WIDTH * MAX_WIDTH; int32_t width; int32_t height; uint8_t data[MAX_SIZE] __attribute__ ((aligned(4))); TetrisFigure &operator = (const TetrisFigure &other); void rotateInto(TetrisFigure &other); void rotate(); }; ... const TetrisFigure TetrisMainScreen::FIGURES[7] = { { 4, 1, { 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 } }, { 3, 2, { 1, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0 } }, { 3, 2, { 0, 1, 1, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 } }, { 3, 2, { 1, 1, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0 } }, { 3, 2, { 1, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 } }, { 3, 2, { 0, 1, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0 } }, { 2, 2, { 1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 } } };
La figura que cae es una copia en RAM de la figura correspondiente de ese array, pues puede ser necesario rotarla. La rotación, como siempre es en pasos de 90 grados, se realiza por la técnica de la transposición y a continuación aplicar función espejo vertical u horizontal, y así no hay que hacer cálculos trigonométricos.
Máquina de estados
La máquina de estados consta de 3 estados:
1. NEW_FIGURE (estado inicial): En este estado se coge la figura siguiente y se intenta colocar en la parte superior del tablero para que vaya cayendo:
1.1. Si se puede colocar, se pasa al estado FALLING y se calcula una nueva figura para que sea la p2róxima siguiente".
1.2. Si no se puede colocar porque ya toca con suelo o con figuras anteriores "consolidadas", se pasa al estado GAME_OVER.
2. FALLING: Este es el estado principal del juego, la figura actual va cayendo y en el momento que se detecta que toca contra suelo o con borde inferior del tablero, la figura se convierte en suelo (se "consolida"). Cuando se detecta que se ha "generado suelo nuevo" se recorre el tablero, se eliminan las filas llenas y se comprueba si se debe subir de nivel.
2.1. Si la figura que está cayendo toca suelo, se pasa al estado NEW_FIGURE.
3. GAME_OVER: Por ahora es un estado "muerto". El juego se cuelga intencionadamente y el jugador debe reiniciar la consola si quiere seguir jugando o empezar de nuevo.
Screen *TetrisMainScreen::onUpdate() { bool boardChanged = false; uint8_t b = this->buttons.getValue(); LevelChanged levelChanged = LevelChanged::NO; if (this->status == St::NEW_FIGURE) { this->generateNewRandomFigure(); this->nextFigureChanged = true; this->figureX = this->rnd.getNextValue() % (10 - this->figure.width); this->figureY = 0; if (this->getFigureValidAt(this->figure, this->figureX, this->figureY)) { this->status = St::FALLING; this->ticksBetweenMovs = this->initialTicksBetweenMovs; boardChanged = true; } else { this->status = St::GAME_OVER; // game over is a dead state (console must be reseted) } } else if (this->status == St::FALLING) { this->ticksBetweenMovs--; if ((this->ticksBetweenMovs <= 0) || (b & Buttons::MASK_DOWN)) { if (this->getCanMoveFigureTo(Direction::DOWN)) { this->figureY++; } else { this->finalizeFigure(levelChanged); this->status = St::NEW_FIGURE; } if (this->ticksBetweenMovs <= 0) this->ticksBetweenMovs = this->initialTicksBetweenMovs; boardChanged = true; } else if ((b & Buttons::MASK_A) && this->getCanRotateFigure()) { this->figure.rotate(); boardChanged = true; } else if ((b & Buttons::MASK_LEFT) && this->getCanMoveFigureTo(Direction::LEFT)) { this->figureX--; boardChanged = true; } else if ((b & Buttons::MASK_RIGHT) && this->getCanMoveFigureTo(Direction::RIGHT)) { this->figureX++; boardChanged = true; } } if (boardChanged) { this->updateBoardWithFigure(); if (levelChanged == LevelChanged::YES) this->drawLevelLabel(); this->drawBoardWithFigureOnFrameBuffer(); if (this->nextFigureChanged) { this->drawNextFigureOnFrameBuffer(); this->nextFigureChanged = false; } this->display.notifyFrameBufferChanged(); } return nullptr; }
Siguiente entrega
En la siguiente entrega se analizará el segundo de los juegos que incluye la consola. Un shooter 3D muy sencillo implementado con la técnica del raycasting
Todo el código y los diseños están en la sección soft.
[ añadir comentario ] ( 268 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |
( 3 / 337 )A lo largo de 4 entradas consecutivas en el blog iré detallando todo el desarrollo y la implementación de una miniconsola de videojuegos portátil que he desarrollado para mi hijo. La idea era hacer una consola al estilo "maquinita" o "game & watch" pero algo más elaborada, alimentada con batería recargable y con algunos juegos prefijados. En esta entrada me centraré en el diseño hardware y el desarrollo de las librerías básicas para acceso al hardware.
Características principales
- Microcontrolador GD32VF103: núcleo RISC-V de 32 bits a 96 MHz, con 256 Kb de Flash y 32 Kb de SRAM.
- Pantalla: Módulo GMG12864 basado en el controlador de display ST7565 de 128x64 pixels en blanco y negro (sin escalas de grises, cada pixel encendido o apagado).
- Botonera: Cruceta (arriba, abajo, izquierda y derecha) más dos botones adicionales (A y B) de funcionalidad personalizable.
- Alimentación: Batería de una celda de LiPo o LiIon de 1200 mAh (3.7 voltios) para unas 6 horas de juego continuado. Recargable mediante módulo de controlador de carga con conector USB-C y con interruptor de encendido.
A continuación una foto del frontal de la consola (encendida aunque aún sin caja).
Y de la parte trasera, donde se puede ver todo el trabajo de soldadura (a muchos técnicos en electrónica seguramente les sangrarán los ojos, pero bueno, hice lo que pude, se me da mejor programar que soldar).
Pantalla
Aprovechando que el microcontrolador tiene una potencia razonable se opta por un modelo de pantalla con una capa de abstracción basada en framebuffer, de tal manera que los juegos de la consola escribirán en un framebuffer de lineal de $128 \times 64 = 8192$ bytes. Para encender o apagar el pixel (x, y) se escribirá un 1 o un 0, respectivamente, en el offset $\left( y \times 128 \right) + x$ del framebuffer:
frameBuffer[(y * 128) + x] = 1; // encender pixel (x, y) frameBuffer[(y * 128) + x] = 0; // apagar pixel (x, y)
Habrá una clase encargada de traducir la información del framebuffer en transferencias SPI al módulo GMG12864 para que se pinte de forma adecuada la pantalla. Esta abstracción nos permite adaptarnos a pantallas futuras y no depender sólo de esa pantalla en concreto, además de que facilita el desarrollo y las pruebas como veremos más adelante.
Botonera
La botonera se implementa con 6 botones mecánicos con el común a masa. Las 6 entradas GPIO en el microcontrolador se configuraon como GPIOs en pullup y así nos ahorramos tener que poner resistencias de pull-up por fuera. Se opta por no poner circuitería antirrebote en los botones para abaratar costes: el antirrebote se realizará por software, mediante una máquina de estados que, con temporizadores, evitará que se produzcan rebotes en la acción de las teclas.
Alimentación
La alimentación es muy sencilla, se utiliza un módulo TP4056 para una celda LiPo o LiIon de 3.7 voltios que ya viene con conector USB-C para carga y salida estabilizada que puede ir directa a la entrada de 5 voltios del módulo del microcontrolador. Toda la consola requiere 3.3 voltios para funcionar pero, como el convertidor de voltaje de la placa del microcontrolador tiene un dropout muy bajo, se pueden meter los 3.7 voltios de salida de la controladora de carga por la entrada de 5 voltios de la placa del microcontrolador. El interruptor de alimentación se coloca en serie con la alimentación que llega al microcontrolador y a la pantalla de tal manera que, aunque el interruptor de la consola esté apagado, su batería se podrá cargar con un cargador estándar USB-C.
Entorno de desarrollo y clases básicas
Como otros desarrollos "grandes" que he hecho siempre intento que el proceso de desarrollo y de depuración sean lo más eficientes posibles y para ello trato siempre de aprovechar el uso de clases abstractas para abstraer el código del hardware específico o la plataforma en la que estoy trabajando. Por ejemplo, para el manejo de la pantalla habrá una clase "Display" que albergará el framebuffer y algunas funciones miembro auxiliares, a continuación se crea una carpeta "gd32vf103" donde irá la implementación específica para el microcontrolador y la pantalla utilizadas "SPIGMG12864Display" que heredará de "Display". Se crea también una carpeta "linux" donde va la implementación específica para Xlib ("XlibDisplay").
A continuación los diagramas de clases de las clases principales del código fuente:
En azul las clases específicas del microcontrolador, en verde las clases específicas de linux y en blanco las clases comunes.
En estos diagramas de clases se pueden ver las clases básicas que constituyen el "framework" de la miniconsola. El elemento central para entender cómo funciona el flujo del software es la clase "Screen" que representa una pantalla (título, menú, un juego en sí, etc.) y la clase "ScreenManager", encargada de ir cambiando de pantallas en función de las necesidades del flujo del programa.
Cada Screen debe implementar las funciones miembro:
void Screen::onLoad(InterScreenData *dataFromPreviousScreen): Esta función se invoca cuando se carga una pantalla, se supone que a partir de este momento el framebuffer es "suyo" por lo que lo lógico en esta función miembro es que se inicialicen variables, se borre el framebuffer, se pinten las partes fijas del mismo, se inicialice la mecánica de esta pantalla, etc.
Screen *Screen::onUpdate(): Esta función se ejecuta cada 20 ms por parte del timer del sistema para que se implementen la mecánica de la pantalla (menú, juego, etc.). Si devuelve *this o nullptr significará que no hay que cambiar de pantalla, en caso contrario significa que queremos cambiarnos a la pantalla correspondiente.
InterScreenData *Screen::onUnload(): Esta función miembro se ejecuta en caso de que la última llamada a "onUpdate()" haya devuelto una "Screen *" válida (no nullptr) y diferente a la actual. La idea es poner aquí código de "terminación" de nuestra pantalla. Un objeto de clase "Screen" puede ser cargado ("onLoad") y descargado ("onUnload") varias veces entre su construcción y su destrucción.
La clase "ScreenManager" heredará de la clase "Task" para implementar la función miembro run, donde se realizará la mecanica del onLoad/onUpdate/onUnload indicada:
class InterScreenData { }; class Screen; class Screen { public: virtual void onLoad(InterScreenData *dataFromPreviousScreen) = 0; virtual Screen *onUpdate() = 0; virtual InterScreenData *onUnload() = 0; }; class ScreenManager : public Task { public: Screen *currentScreen; ScreenManager(Screen &initialScreen, InterScreenData *initialInterScreenData); virtual void run(); }; ScreenManager::ScreenManager(Screen &initialScreen, InterScreenData *initialInterScreenData) : currentScreen(&initialScreen) { this->currentScreen->onLoad(initialInterScreenData); } void ScreenManager::run() { Screen *nextScreen = this->currentScreen->onUpdate(); if ((nextScreen != this->currentScreen) && (nextScreen != nullptr)) { InterScreenData *isd = this->currentScreen->onUnload(); nextScreen->onLoad(isd); this->currentScreen = nextScreen; } }
Como se puede ver es una mecánica muy sencilla. A partir de la clase "Screen" se crean todas las pantallas de la aplicación, por ejemplo:
- SplashScreen: Pantalla de bienvenida con una imagen de fondo y un texto de copyright que espera a que pulses un botón para pasar a la siguiente pantalla.
- MenuScreen: Pantalla de menú que permite, a su vez, especializarse para crear diferentes menus (como MainMenuScreen).
- ...
Cualquier clase que herede de Screen y que implemente los tres métodos especificados será otro tipo de pantalla con la funcionalidad que queramos.
Esta forma de programar la aplicación es muy escalable y permite crear fácilmente flujos de código muy elaborados:
int main() { // init hardware interruptInit(); RGBLed::init(); GPIOButtons buttons; Random random(buttons); SPIGMG12864Display display; display.blank(); // create screens InitialSplashScreen initialSplashScreen(display, buttons); MainMenuScreen mainMenuScreen(display, buttons); TetrisMainScreen tetrisMainScreen(display, buttons, random); TanksMainScreen tanksMainScreen(display, buttons, random); SnakeMainScreen snakeMainScreen(display, buttons, random); SnoopyMainScreen snoopyMainScreen(display, buttons, random); // link screens initialSplashScreen.setNextScreen(mainMenuScreen); mainMenuScreen.setBackScreen(initialSplashScreen); mainMenuScreen.setTetrisScreen(tetrisMainScreen); mainMenuScreen.setTanksScreen(tanksMainScreen); mainMenuScreen.setSnakeScreen(snakeMainScreen); mainMenuScreen.setSnoopyScreen(snoopyMainScreen); // main loop ScreenManager m(initialSplashScreen, nullptr); MyListener myListener(display, buttons, m); Timer::init(myListener, 20_msForTimer); while (true) asm volatile ("wfi"); }
No se usan variables globales (no son necesarias):
1. Se inicializa el hardware: el controlador de interrupciones, la pantalla, la botonera y el generador de números pseudoaleatorios.
2. Se construyen todas las pantallas: A todas les pasamos el objeto display y el objeto buttons (a algunas de ellas se les pasa el generador del números pseudoaleatorios).
3. Se enlazan las pantallas: Cada objeto de clase Screen debe tener los punteros a las pantallas hacia las que puede irse a partir de él. Por ejemplo, la pantalla initialSplashScreen debe saber que debe ir a la pantalla mainMenuScreen cuando pulsen un botón. De la misma forma la pantalla de menú, que debe saber a qué pantalla se salta con cada opción.
4. Justo antes del bucle principal: Se le indica al ScreenManager cual es pantalla inicial (la que debe aparecer en el arranque).
5. Bucle principal: En este caso, para ahorrar energía, no se hace el típico bucle "while (true)" sino que se programa el timer del sistema para dispararse cada 20 milisegundos y en la función miembro "timerExpired" del objeto escuchador del timer, se invoca la máquina el "run" de los botones y el "run" del ScreenManager, que es la función miembro encargada de gestionar las pantallas (llamar a onLoad/onUpdate/onUnload de las pantallas). Haciendo el bucle principal podemos utilizar la instrucción ensamblador "wfi" (wait for interrupt) para que, entre iteraciones, el procesador pueda dormirse y así evitar que se consuma mucha batería.
Siguiente entrega
En la siguiente entrega se analizará el diseño y la implementación del Tetris (uno de los cuatro juegos que incluye la miniconsola).
Todo el código y los diseños están en la sección soft.
[ añadir comentario ] ( 356 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |
( 3 / 336 )
Calendario
