Se trata de una toolchain para sistemas "bare metal", sin sistema operativo, por lo que no tiene soporte para multihilos ni para librerías dinámicas.
binutils 2.36
mkdir -p /opt/baremetalriscv/src
mkdir -p /opt/baremetalriscv/build
cd /opt/baremetalriscv/src
wget https://ftp.gnu.org/gnu/binutils/binutils-2.36.tar.bz2
tar xf binutils-2.36.tar.bz2
cd ../build
mkdir binutils-2.36
cd binutils-2.36/
../../src/binutils-2.36/configure --prefix=/opt/baremetalriscv --target=riscv32-none-elf --disable-nls
make
make install
gcc 11.1.0 (stage 1)
cd /opt/baremetalriscv/src
wget https://ftp.gnu.org/gnu/gcc/gcc-11.1.0/gcc-11.1.0.tar.gz
wget https://ftp.gnu.org/gnu/gmp/gmp-6.2.1.tar.bz2
wget https://ftp.gnu.org/gnu/mpc/mpc-1.2.1.tar.gz
wget https://ftp.gnu.org/gnu/mpfr/mpfr-4.1.0.tar.gz
tar xf gcc-11.1.0.tar.gz
tar xf gmp-6.2.1.tar.bz2
tar xf mpc-1.2.1.tar.gz
tar xf mpfr-4.1.0.tar.gz
mv gmp-6.2.1 gcc-11.1.0/gmp
mv mpc-1.2.1 gcc-11.1.0/mpc
mv mpfr-4.1.0 gcc-11.1.0/mpfr
cd ../build/
mkdir gcc-11.1.0-stage-1
cd gcc-11.1.0-stage-1/
export PATH=/opt/baremetalriscv/bin:${PATH}
../../src/gcc-11.1.0/configure --prefix=/opt/baremetalriscv --target=riscv32-none-elf --enable-languages=c --without-headers --disable-nls --disable-threads --disable-shared --disable-libssp --with-newlib
make all-gcc all-target-libgcc
make install-gcc install-target-libgcc
newlib
cd /opt/baremetalriscv/src
git clone git://github.com/riscv/riscv-newlib.git
cd ../build
mkdir newlib
cd newlib
../../src/riscv-newlib/configure --prefix=/opt/baremetalriscv --target=riscv32-none-elf
make
make install
gcc 11.1.0 (stage 2)
cd /opt/baremetalriscv/build
mkdir gcc-11.1.0-stage-2
cd gcc-11.1.0-stage-2/
../../src/gcc-11.1.0/configure --prefix=/opt/baremetalriscv --target=riscv32-none-elf --enable-languages=c,c++ --disable-nls --disable-threads --disable-shared --disable-libssp --with-newlib --with-headers=../../src/riscv-newlib/newlib/libc/include
make
make install
El compilador de C++ de GCC 11.1 compila por defecto en modo C++17 y soporta prácticamente todo el estándar C++20.
ACTUALIZACIÓN: El proceso de compilación descrito sirve también para gcc-12.2, binutils-2.40 y el repositorio de newlib oficial (git://sourceware.org/git/newlib-cygwin.git) puesto que el proyecto riscv-newlib ya se ha integrado en el proyecto oficial de newlib.
[ añadir comentario ] ( 1312 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 2116 )
( 3 / 2116 )La literatura existente relacionada con el diseño de filtros digitales suele incidir en el estudio de determinados filtros ya conocidos, como paso-bajo, paso-alto, paso-banda, etc., a veces calculados a partir de la discretización de filtros analógicos y sin entrar en detalles de diseño o sin abordar el problema de forma directa (sin discretizar). A lo largo de este artículo se abordará el diseño directo de un filtro resonante sencillo.
Plano z
La herramienta fundamental para el cálculo de filtros digitales es la transformada Z y su plano complejo asociado, denominado "plano z". Se asume que el lector está medianamente familiarizado con la transformada z y no se abordarán los detalles ni las propiedades de la misma.
La transformada z transforma una función, situada en el dominio discreto del tiempo $x[n]$, en otra función, situada en el dominio complejo de z $X(z)$. Esta transformación es equivalente a la transformada de Laplace en el dominio continuo y tiene ambas propiedades similares en cuanto a linealidad y estabilidad. Al igual que la transformada de Laplace, la transformada Z también se utiliza para modelar funciones de transferencia de sistemas, en el caso de la transformada Z, son sistemas discretos.
Es decir, si para un filtro analógico tenemos una función de transferencia $H(s)$, caracterizada principalmente por sus ceros y sus polos, para un filtro digital tendremos también una función de transferencia $H(z)$, caracterizada también por sus ceros y sus polos. Tanto en el caso de Laplace como en el caso Z los ceros determinan para qué tipo de señales el filtro "tiende a cancelar la entrada" y los polos determinan para qué tipo de señales el filtro "tiende a amplificar la entrada" o incluso entrar en resonancia. La regla básica que debe cumplirse en un filtro analógico es que los polos de $H(s)$ nunca deben tener parte real positiva (deben estar siempre localizados en el semiplano izquierdo del plano complejo $s$), mientras que en caso de un filtro digital, los polos de $H(z)$ nunca deben alojarse fuera de la circunferencia unitaria centrada en el origen del plano complejo $z$ (es decir, los polos en un filtro digital deben cumplir que $|z| < 1$).
Diseño de un filtro resonante sencillo
En el plano z no se mapean frecuencias absolutas como en el plano s, sino que se mapean frecuencias "relativas" a la frecuencia de muestreo y a lo largo de la longitud de la circunferencia de radio 1. La frecuencia asociada a un valor complejo del plano z se corresponde con el ángulo (argumento) de dicho valor: un ángulo de 0 radianes se corresponde con un valor en continua (0 Hz) mientras que un valor de $\pi$ radianes se corresponde con la mitad de la frecuencia de muestreo (frecuencia Nyquist). Si, por ejemplo, muestreamos a 44100 Hz, la frecuencia máxima ($\pi$) será de 22050 Hz, mientras que si muestreamos a 8000 Hz la misma frecuencia PI se corresponderá con 4000 Hz.
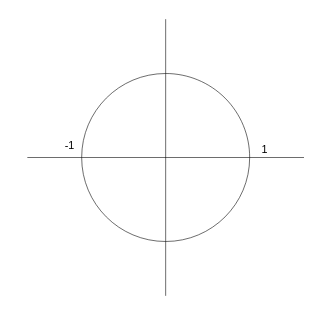
El diseño básico de filtros digitales es muy sencillo y se resume en cuatro reglas principales:
- Alojar tantos ceros sobre la circunferencia de radio 1 como frecuencias queramos cancelar. Lo importante de cada cero será su ángulo (= frecuencia) con respecto al origen. Por ejemplo si colocamos un cero en en punto $z = 1$, que se corresponde con un ángulo de 0 radianes, nuestro filtro eliminará la componente de continua de la señal.
- Alojar tantos polos DENTRO de la circunferencia de radio 1 ($|z| < 1$) como frecuencias queramos amplificar. En este caso es importante tanto el ángulo (= frecuencia que queremos reforzar) como su magnitud o módulo (= nivel de refuerzo). Si hacemos que la magnitud (el módulo) de un polo sea 1 ($|z| = 1$) el filtro auto-oscilará a esa frecuencia. Por ejemplo, si colocamos un polo en $z = -1$, que se corresponde con un ángulo $\pi$, estaremos reforzando las señales con frecuencia próxima a $\pi$ (= la mitad de la frecuencia de muestreo).
- Los polos y ceros que tengan parte imaginaria diferente de 0 deberán ponerse por pares conjugados para poder trabajar con señales reales (sin componente imaginaria). Por ejemplo, si estamos muestreando a 44100 Hz y queremos cancelar las frecuencias próximas a 11025 Hz (frecuencia ${\pi \over 2}$), debemos colocar DOS polos conjugados: uno en $(0, 1)$, formando un ángulo de 90 grados (${\pi \over 2}$) y otro en $(0, -1)$ (su conjugado).
- Al final lo habitual es también ajustar la ganancia global del filtro (aunque en este caso no lo hemos hecho por simplicidad). Esto se hace habitualmente debido a que a veces los polos meten mucha ganancia en la banda de paso y es necesario escalar la salida antes de emitirla o la entrada antes de procesarla.
Si, por ejemplo, queremos hacer un filtro paso bajo, lo habitual, es poner un cero en $z = -1$ (sobre la circunferencia de radio 1 con ángulo $\pi$) con el objetivo de anular las altas frecuencias y un polo (con su complejo conjugado) cerca de la frecuencia de corte de nuestro filtro. En nuestro caso de estudio, se trata de un filtro resonante sencillo, por lo que definiremos dos ceros: uno en $z = 1$ (0 radianes), y otro en $z = -1$, ($\pi$ radianes). Como queremos una única frecuencia de resonancia, definimos un único polo (junto con su complejo conjugado, por lo que realmente serán dos polos).
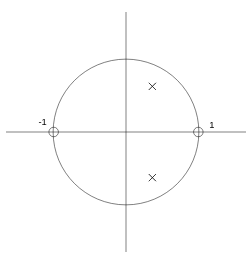
Con esta configuración de dos ceros reales en -1 y 1 y dos polos complejos conjugados en la frecuencia de resonancia tenemos la siguiente función de transferencia en Z:
$$H(z) = {(z + 1)(z - 1) \over (z - p_1)(z - p_1^\prime)}$$
Para la que se cumple que:
$$p_1 = a + bi \;\;\;\;\;\;\;\;\; p_1^\prime = a - bi$$
Desarrollando el denominador (los polos) de $H(z)$ tenemos que:
$$(z - p_1)(z - p_1^\prime) = z(z - p_1^\prime) - p_1(z - p_1^\prime)$$
$$ = z^2 - zp_1^\prime -p_1z + p_1p_1^\prime$$
$$ = z^2 - z(p_1^\prime + p_1) + p_1p_1^\prime$$
$$ = z^2 - z2a + p_1p_1^\prime$$
$$ = z^2 - z2a + a^2 + b^2$$
Nótese que, al ser los polos complejos conjugados, las operaciones
$(p_1^\prime + p_1)$ y $p_1p_1^\prime$ dan como resultado, valores reales (sin componente imaginaria). Por otro lado, si desarrollamos el numerador (los ceros) de $H(z)$ tenemos que:
$$(z + 1)(z - 1) = z(z - 1) + (z - 1)$$
$$ = z^2 - z + z - 1$$
$$ = z^2 - 1$$
Por tanto la función de transferencia $H(z)$ puede reescribirse de la siguiente manera:
$$H(z) = {{z^2 - 1} \over {z^2 - z2a + a^2 + b^2}}$$
Podemos visualizar la respuesta en frecuencia de este sistema asignando a z diferentes valores sobre la circunferencia unitaria $z = e^{iw} = cos(w) + i sen(w)$:
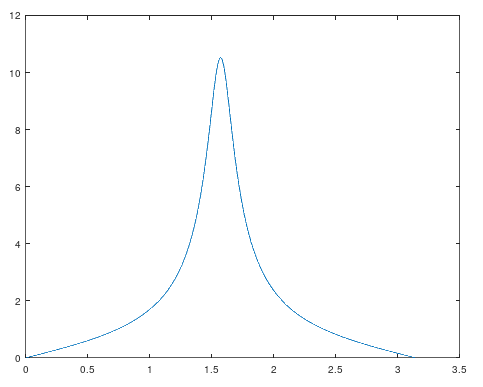
Para generar esta gráfica se ejecutó el siguiente código octave que sitúa el polo (= la frecuencia de resonancia del filtro) en ${\pi \over 2}$:
m = 0.9; w = pi / 2; a = m * cos(w); b = m * sin(w); # respuesta en frecuencia TAM = 1000; responseX = zeros(1, TAM); responseY = zeros(1, TAM); for n = 1:TAM w = (n / TAM) * pi; responseX(n) = w; z = cos(w) + (i * sin(w)); responseY(n) = abs(((z * z) - 1) / ((z * z) - (z * 2 * a) + (a * a) + (b * b))); endfor plot(responseX, responseY);
Implementación del filtro
Ahora que ya tenemos la función de transferencia en el dominio Z del filtro que queremos, el siguiente paso es pasar al dominio discreto y calcular los coeficientes en diferencias finitas para poder implementarlo. Lo primero que se hace es evitar que haya exponentes mayores que 0 para z (exponentes positivos de z se corresponden a muestras "futuras" en el tiempo). Esto se soluciona de forma muy sencilla multiplicando numerador y denominador de $H(z)$ por $z^{-2}$, esto mantiene $H(z)$ igual pero elimina los exponentes positivos:
$$H(z) = {{z^2 - 1} \over {z^2 - z2a + a^2 + b^2}}$$
$$H(z) = {{z^{-2}(z^2 - 1)} \over {z^{-2}(z^2 - z2a + a^2 + b^2)}}$$
$$H(z) = {{1 - z^{-2}} \over {1 - z^{-1}2a + z^{-2}(a^2 + b^2)}}$$
Ahora ya podemos calcular los coeficientes de forma más sencilla. Como $H(z)$ es una función de transferencia en Z tenemos que, si $X(z)$ es la transformada Z de la entrada e $Y(z)$ es la transformada Z de la salida, entonces:
$$Y(z) = H(z) X(z) = {{1 - z^{-2}} \over {1 - z^{-1}2a + z^{-2}(a^2 + b^2)}} X(z)$$
Y, por tanto:
$$Y(z)(1 - z^{-1}2a + z^{-2}(a^2 + b^2)) = X(z)(1 - z^{-2})$$
$$Y(z)-Y(z)z^{-1}2a+Y(z)z^{-2}(a^2 + b^2) = X(z) - X(z)z^{-2}$$
Como la transformada Z es lineal y se cumple que la transformada Z de un valor desplazado k muestras en el tiempo es la siguiente:
$$Z \left\{ x[n - k] \right\} = X(z)z^{-k}$$
Entonces podemos hacer la antitransformada Z de forma sencilla:
$$y[n] - y[n - 1]2a + y[n - 2](a^2 + b^2) = x[n] - x[n - 2]$$
Y, despejando $y[n]$ tenemos que:
$$y[n] = x[n] - x[n - 2] + y[n - 1]2a - y[n - 2](a^2 + b^2)$$
Esto, como se puede ver, es una ecuación en diferencias finitas, que es muy fácil de implementar tanto en hardware como en software. Veamos una ejemplo de código octave que genera ruido blanco y luego lo hace pasar por el filtro (aplica la ecuación en diferencias finitas con los mismos valores a y b, esto es, misma frecuencia de resonancia en ${\pi \over 2}$).
m = 0.9; w = pi / 2; a = m * cos(w); b = m * sin(w); TAM = 1000; input = (rand(1, N) .* 2) .- 1; # TAM valores aleatorios entre -1 y 1 ym1 = 0; ym2 = 0; xm1 = 0; xm2 = 0; output = zeros(1, TAM); for n = 1:TAM output(n) = input(n) - xm2 + (ym1 * 2 * a) - (ym2 * ((a * a) + (b * b))); ym2 = ym1; ym1 = output(n); xm2 = xm1; xm1 = input(n); endfor subplot(2, 2, 1) plot(input); title('Ruido'); subplot(2, 2, 2) plot(output); title('Ruido filtrado'); subplot(2, 2, 3) plot(abs(fft(input)(1:(N / 2)))); title('Espectro del ruido'); subplot(2, 2, 4) plot(abs(fft(output)(1:(N / 2)))); title('Espectro del ruido filtrado');
A continuación se pueden ver las señales y los espectros en frecuencia de las mismas y se puede comprobar como el funcionamiento del filtro es el esperado:
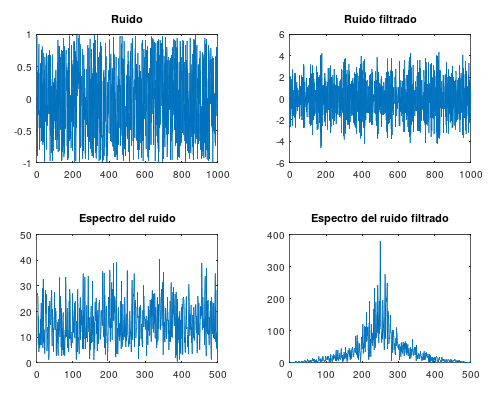
[ añadir comentario ] ( 2336 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 2138 )
( 3 / 2138 )El proyecto navideño de este año es una sencilla estrella de navidad que puede colocarse tanto en el árbol como en el belén y que requiere de muy poca circuitería.
Idea
El objetivo era no recurrir a la típica luz parpadeante sino darle un efecto de movimiento, que parezca que la estrella se mueva por el firmamento. Para simular este efecto lo más sencillo es alinear varias luces y hacer que la luz se mueva rápidamente, con un brillo creciente y en una dirección concreta, lo que da el efecto de que la luz un efecto meteorito.
Diseño eléctrico
A nivel electrónico el concepto es muy sencillo: 8 leds de alta luminosidad protegidos con resistencias y conectados a 8 salidas de un CPLD.
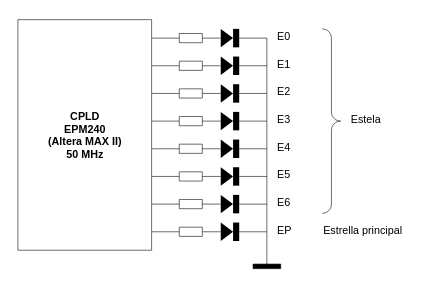
Uno de los leds hace de estrella principal mientras que los 7 leds restantes servirán para hacer el efecto de la estela de la estrella principal. La secuencia de iluminación será la siguiente:
- E0 iluminado al 5%, resto apagado
- E1 iluminado al 10%, resto apagado
- E2 iluminado al 15%, resto apagado
- E3 iluminado al 20%, resto apagado
- E4 iluminado al 30%, resto apagado
- E5 iluminado al 40%, resto apagado
- E6 iluminado al 50%, resto apagado
- EP iluminado al 100% durante varias unidades de tiempo más, resto apagado
- Todo apagado durante varias unidades de tiempo
Diseño lógico y funcionamiento
A continuación una propuesta de diagrama de bloques sencillo:
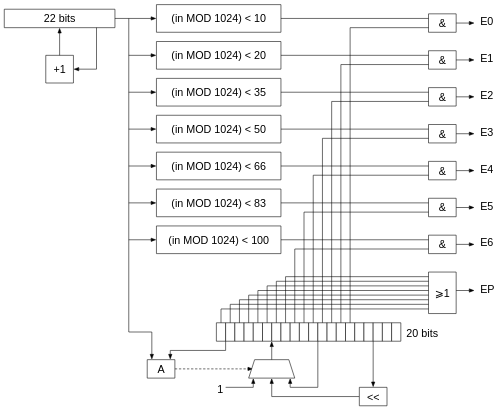
Al circuito combinacional A tiene como entradas el valor del registro contador de 22 bits y el valor del registro de desplazamiento de 20 bits y como salida la entrada de selección del multiplexor del registro de desplazamiento de 20 bits:
| registro contador | reg. desplaz. | mux |
|---|---|---|
| x | 0 | valor 1 |
| 0 | x | salida desplazador izquierda |
| ≠0 | ≠0 | reg. desplaz. (mantener) |
El registro contador se utiliza con dos propósitos:
- Como medida de unidad de tiempo: Cada vez que se desborda, se desplaza el registro de desplazamiento. A 50 MHz de frecuencia de reloj, tenemos una frecuencia de desplazamiento de ${50000000 \over {2^{22}}} = 11.92093 \: Hz$, es decir ${1 \over 11.92093} = 0.08389 \: seg$, aproximadamente una décima de segundo como unidad de tiempo.
- Como registro contador para el PWM de los leds de la estela: Como es un contador estándar de desbordamiento, se pueden usar los 10 bits menos significativos para generar una señal PWM, esto nos da una frecuencia de señal PWM de ${50000000 \over {2^{10}}} \approx 49 \: KHz$ que es una buena frecuencia para un led.
Al iniciarse el CPLD todos los bits del registro de desplazamiento estarán a 0, lo que provocará que el circuito combinacional A emita un 1 para que, en el primer ciclo de reloj, se cargue un 1 en el registro de desplazamiento. A partir de aquí el circuito combinacional A mantendrá el multiplexor en modo "copia" (manteniendo el valor del registro de desplazamiento) y sólo mandará a desplazar cuando el registro contador se desborde. El registro de desplazamiento tendrá un bit 1 moviéndose de izquierda a derecha a razón de un salto cada décima de segundo, cuando el bit llega al extremo izquierdo aparece de nuevo en el extremo derecho del registro (formalmente deberíamos llamar al registro de desplazamiento, registro de "rotación").
Los 5 bits menos significativos del registro de desplazamiento no se conectan a nada, lo que significa que durante unas 5 décimas de segundo (medio segundo aproximadamente) ninguna de las luces se enciende, cuando el 1 pasa al bit 5 del registro de desplazamiento, se pone a 1 la entrada inferior de la puerta AND que gobierna el led E0, que hace las veces de enable para la salida PWM con menor ciclo de trabajo (menor luminosidad). Cuando el 1 pasa al bit 6 del registro de desplazamiento, se pone a 1 la entrada inferior de la puerta AND que gobierna el led E1, que hace de enable para la salida PWM con ciclo de trabajo ligeramente superior (un poco más de limunosidad que el anterior) y así sucesivamente. A medida que el 1 va desplazándose a la izquierda (un salto por cada décima de segundo aproximadamente) se van iluminando los leds E0 a E6 de forma consecutiva y con ciclos de trabajo PWM crecientes (es decir, cantidad de luz creciente). Los últimos 8 bits del registro de desplazamiento (bits 19 al 12) están conectados a una puerta OR que gobierna la luz EP (estrella principal), esto hace que la estrella principal esté encendida unas 8 décimas de segundo, y luego vuelta a empezar.
Implementación
A continuación el código VHDL:
library ieee; use ieee.std_logic_1164.all; use ieee.numeric_std.all; entity MaxIIBethlehemStar is port ( ClkIn : in std_logic; BoardLedOut : out std_logic; StarOut : out std_logic; Wake1Out : out std_logic; Wake2Out : out std_logic; Wake3Out : out std_logic; Wake4Out : out std_logic; Wake5Out : out std_logic; Wake6Out : out std_logic; Wake7Out : out std_logic ); end entity; architecture A of MaxIIBethlehemStar is constant Intensity1PWM : integer := 100; -- over 1024 constant Intensity2PWM : integer := 83; constant Intensity3PWM : integer := 66; constant Intensity4PWM : integer := 50; constant Intensity5PWM : integer := 35; constant Intensity6PWM : integer := 20; constant Intensity7PWM : integer := 10; signal TimerDBus : std_logic_vector(21 downto 0); signal TimerQBus : std_logic_vector(21 downto 0); signal ShiftDBus : std_logic_vector(19 downto 0); signal ShiftQBus : std_logic_vector(19 downto 0); signal Intensity1 : std_logic; signal Intensity2 : std_logic; signal Intensity3 : std_logic; signal Intensity4 : std_logic; signal Intensity5 : std_logic; signal Intensity6 : std_logic; signal Intensity7 : std_logic; begin -- intensity signals (using timer lower 10 bits as PWM counter) Intensity1 <= '0' when (unsigned(TimerQBus(9 downto 0)) > to_unsigned(Intensity1PWM, 10)) else '1'; Intensity2 <= '0' when (unsigned(TimerQBus(9 downto 0)) > to_unsigned(Intensity2PWM, 10)) else '1'; Intensity3 <= '0' when (unsigned(TimerQBus(9 downto 0)) > to_unsigned(Intensity3PWM, 10)) else '1'; Intensity4 <= '0' when (unsigned(TimerQBus(9 downto 0)) > to_unsigned(Intensity4PWM, 10)) else '1'; Intensity5 <= '0' when (unsigned(TimerQBus(9 downto 0)) > to_unsigned(Intensity5PWM, 10)) else '1'; Intensity6 <= '0' when (unsigned(TimerQBus(9 downto 0)) > to_unsigned(Intensity6PWM, 10)) else '1'; Intensity7 <= '0' when (unsigned(TimerQBus(9 downto 0)) > to_unsigned(Intensity7PWM, 10)) else '1'; -- timer counter process (ClkIn) begin if (ClkIn'event and (ClkIn = '1')) then TimerQBus <= TimerDBus; end if; end process; TimerDBus <= std_logic_vector(unsigned(TimerQBus) + to_unsigned(1, 22)); -- shift register process (ClkIn) begin if (ClkIn'event and (ClkIn = '1')) then ShiftQBus <= ShiftDBus; end if; end process; ShiftDBus <= std_logic_vector(to_unsigned(1, 20)) when (unsigned(ShiftQBus) = 0) else ShiftQBus(18 downto 0) & ShiftQBus(19) when (unsigned(TimerQBus) = 0) else ShiftQBus; -- outputs StarOut <= ShiftQBus(19) or ShiftQBus(18) or ShiftQBus(17) or ShiftQBus(16) or ShiftQBus(15) or ShiftQBus(14) or ShiftQBus(13) or ShiftQBus(12); Wake1Out <= Intensity1 and ShiftQBus(11); Wake2Out <= Intensity2 and ShiftQBus(10); Wake3Out <= Intensity3 and ShiftQBus(9); Wake4Out <= Intensity4 and ShiftQBus(8); Wake5Out <= Intensity5 and ShiftQBus(7); Wake6Out <= Intensity6 and ShiftQBus(6); Wake7Out <= Intensity7 and ShiftQBus(5); -- debug BoardLedOut <= (ShiftQBus(19) or ShiftQBus(18) or ShiftQBus(17) or ShiftQBus(16) or ShiftQBus(15) or ShiftQBus(14) or ShiftQBus(13) or ShiftQBus(12)) or (Intensity1 and ShiftQBus(11)) or (Intensity2 and ShiftQBus(10)) or (Intensity3 and ShiftQBus(9)) or (Intensity4 and ShiftQBus(8)) or (Intensity5 and ShiftQBus(7)) or (Intensity6 and ShiftQBus(6)) or (Intensity7 and ShiftQBus(5)); end architecture;
El montaje se ha implementado sobre un CPLD MAX II de Altera, usando leds blancos de alta luminosidad y montándolos luego sobre una base de cartón duro con la típica forma de estrella de navidad.

El código fuente está disponible en la sección soft. ¡Feliz Navidad y feliz 2021!
[ añadir comentario ] ( 1602 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 2124 )
( 3 / 2124 )En anteriores entradas se realizó la implementación, tanto de un transmisor FM como de un conversor analógico digital delta-sigma, sobre FPGA y como proyectos separados. A lo largo de esta entrada se aborda el desarrollo de un transmisor FM en la banda de la radio comercial para transmitir música, combinando ambos proyectos en uno solo.
Conversión analógica digital delta-sigma
Como se puede comprobar en el post anterior relacionado, la conversión analógica digital de tipo delta-sigma tiene la ventaja de requerir muy pocos componentes externos: un comparador analógico (para lo que puede usarse un amplificador operacional normal), un condensador y una resistencia; y permite implementar un ADC de precisión arbitraria (la precisión sólo está limitada por los recursos disponibles en la FPGA).
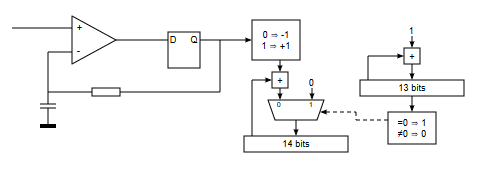
Recordemos que la conversión analógico digital de tipo delta-sigma lo que hace es, mediante un biestable de tipo D, hacer que la salida que carga el condensador C a través de la resistencia R "siga" a la entrada analógica:
- Si la entrada + del comparador está por encima de la entrada -, el comparador emite un 1, que es cargado en el siguiente ciclo de reloj por el biestable de entrada, haciendo que la salida que va a la resistencia R tome el valor de 1 y trate de "acercar" el valor de la entrada - del comparador al valor de la entrada + del comparador.
- Si la entrada + del comparador está por debajo de la entrada -, el comparador emite un 0, que es cargado en el siguiente ciclo de reloj por el biestable de entrada, haciendo que la salida que va a la resistencia R tome el valor de 0 y trate de "acercar" (esta vez hacia "abajo") el valor de la entrada - del comparador al valor de la entrada + del comparador.
Como se puede ver, este comportamiento hace que para valores próximos a 0 voltios en la entrada + del comparador, el biestable de entrada emite muchos más 0s que 1s, mientras que para valores próximos a 3.3 voltios en la entrada + del comparador, el biestable de entrada emite muchos más 1s que 0s. También se puede ver que para valores próximos a Vcc / 2 = 1.65 voltios, el biestable emitirá una cantidad aproximadamente igual de 0s que de 1s.
Si lo que hacemos ahora es asociar al valor 0 de la salida del biestable, el valor numérico -1, y, al valor 1 de la salida del biestable, el valor numérico +1, lo que tenemos es un circuito digital que emitirá:
- Más +1 que -1 para valores próximos a 3.3 voltios.
- Más -1 que +1 para valores próximos a 0 voltios.
- Una cantidad aproximadamente igual de -1 y +1 para valores próximos a 1.65 voltios.
Si vamos acumulando estos -1 y +1 sobre un acumulador que se pone a cero cada cierto tiempo, lo que tendremos es que en dicho acumulador tendremos un valor proporcional al voltaje de entrada del ADC:
- Valores próximos a 3.3 voltios, al generar más +1 que -1, dan como resultado un valor de conversión muy alto y positivo.
- Valores próximos a 0 voltios, al generar más -1 que +1, dan como resultado un valor de conversión muy bajo y negativo.
- Valores próximos a 1.65 voltios, al generar una cantidad aproximadamente similar de -1 y de +1, dan como resultado un valor de conversión próximo a 0.
Debido a esta necesidad de contar -1s y +1s necesitamos sobremuestreo: Si queremos obtener una resolución de 16 bits, eso significa que el valor máximo de conversión tendrá que ser -32767 mientras que el valor mínimo de conversión tendrá que ser -32768. Si asumimos una escala simétrica tendremos un valor entre -32767 y +32767, eso significa que debemos hacer 32767 sumas (de -1s y +1s) antes de leer el valor de conversión. Dichas sumas las tenemos que hacer en un registro, que llamaremos "acumulador de conversión".
Para el caso de 16 bits necesitaríamos un contador de 15 bits que, en el momento de que valga 0 haga que el "acumulador de conversión" copie su valor en el registro de salida del ADC y se ponga a cero, y, durante los 32767 pulsos restantes (hasta el siguiente desbordamiento), se sumen los -1s y +1s que van entrando.
Así vemos que, por ejemplo, para 12 MHz y 16 bits de resolución, como necesitaríamos un contador de 15 bits, al final la frecuencia de muestreo podrá ser, como máximo de:
$$ {12000000 \over {2^{15}}} = 366.21 \: Hz $$
Por ejemplo, si queremos hacer una conversión en calidad CD necesitaríamos un reloj de sistema (sobremuestreo) de:
$$ {44100 \times {2^{15}}} = 1445068800 \: Hz $$
En el caso que nos ocupa se ha decidido implementar el transmisor en una FPGA MAX10 de las que viene en una placa MAX1000 de Arrow, a 12 MHz, cuyo reloj puede ser subido mediante PLLs hasta unos 400 MHz. Debido a esta limitación se ha decidido subir el reloj a 300 MHz y, para trabajar con esa frecuencia de sobremuestreo, se han tenido que bajar un poco las especificaciones del ADC, usando un contador de 13 bits y un acumulador de conversión de 14 bits. De esta forma tenemos una frecuencia de muestreo de:
$$ {300000000 \over {2^{13}}} = 36621.09375 \: Hz $$
Por lo que el ancho de banda es de unos 18 KHz (buen ancho de banda para música) y la resolución de conversión es de 14 bits (valores de conversión entre -8191 y +8191). No es calidad CD pero tampoco está mal.
Consideraciones entorno a la entrada de sonido analógica
Hay que tener en cuenta que las señales de sonido tal cual salen de un amplificador, son señales simétricas (con semiciclos positivos y negativos) mientras que nuestro ADC mide voltajes entre 0 y 3.3 voltios (no mide voltajes negativos). Es necesario, por tanto, acondicional la señal de sonido de entrada para que quede "desplazada" hacia arriba y un valor de 0 voltios de entrada se traduzca en 1.65 voltios a la entrada + del comparador. Es por esto por lo que se coloca el divisor de tensión entre 3.3 y 0 voltios a la entrada de audio, que desplaza el "0" de la señal de sonido hasta los 1.65 voltios.
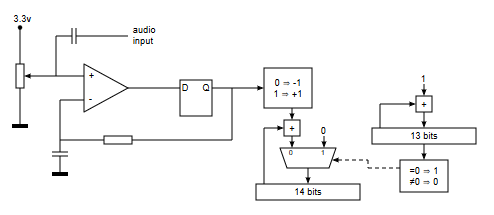
El nivel de señal que entrega la salida de auriculares de un ordenador es suficiente para la entrada del ADC y no requiere amplificación adicional, al menos para esta prueba.
Generador de señal de antena
La frecuencia de transmisión elegida es 87.5 MHz (el extremo inferior de la banda de radiodifusión de sonido). La señal de antena que se quiere generar debe estar centrada, por tanto, en dicha frecuencia y dicha frecuencia deberá variarse en un rango máximo de +-75 KHz (estándar de radiodifusión). Para la generación de frecuencias arbitrarias que sean inferiores a la frecuencia de reloj de un sistema digital lo lógico es utilizar un acumulador de fase.
Un acumulador de fase no es más que un registro que se incrementa en un valor constante (no tiene por qué incrementarse de 1 en 1) con desbordamiento. Por ejemplo, si a partir de un reloj de 300 MHz queremos generar un reloj de 75 MHz lo que podemos hacer es incrementar un registro de 2 bits de 1 en 1 a 300 MHz:
...
Pulso: 00 --> 01
Pulso: 01 --> 10
Pulso: 10 --> 11
Pulso: 11 --> 00
Pulso: 00 --> 01
Pulso: 01 --> 10
Pulso: 10 --> 11
Pulso: 11 --> 00
...
En este ejemplo se puede ver que si la frecuencia de pulso es de 300 MHz, la frecuencia del bit 0 será de ${300 \over 2} = 150 \: MHz$ mientras que la frecuencia del bit 1 será de ${150 \over 2} = 75 \: MHz$. Un acumulador de fase con incrementos potencia de 2 es, formalmente, un divisor de frecuencia. Si se aplica este mismo principio para registros con mayor cantidad de bits y usando incrementos arbitrarios, conseguimos frecuencias diferentes.
Asumamos que la señal de salida de nuestro "oscilador" será siempre el bit más significativo de un registro de 16 bits y nuestro reloj va a 300 MHz. Eso significará que, incrementando el registro de 1 en 1, el bit más significativo cambiará a razón de:
$$ {300000000 \over {2^N}} = 4577 \: Hz $$
Si en lugar de incrementar el registro de 1 en 1, lo incrementamos de 2 en 2, la cantidad de pulsos que tarde en desbordarse el registro será menor, por tanto, la frecuencia del bit más significativo será mayor, es decir, la frecuencia del bit más significativo es proporcional al valor de incremento del registro. El máximo valor de incremento será $2^{N-1}$ para N bits (es decir un 1 seguido de N-1 ceros) que hará que el registro se comporte de la siguiente manera:
...
Pulso: 0000000000000000 --> 1000000000000000
Pulso: 1000000000000000 --> 0000000000000000
Pulso: 0000000000000000 --> 1000000000000000
Pulso: 1000000000000000 --> 0000000000000000
...
En este caso extremo tenemos que la frecuencia del bit más significativo es de 150 MHz (para una frecuencia de pulso de 300 MHz). De forma genérica tenemos que el valor de incremento para una frecuencia dada puede calcularse de la siguiente forma:
$$ I = {{f_{deseada}} \over 300000000} \times 2^{N} $$
En nuestro caso, si queremos emitir a 87.5 MHz hay que usar un valor de N=54 bits para que el valor de incremento no sea fraccionario:
$$ I_{central} = {87500000 \over 300000000} \times 2^{54} = 5254199565265579 $$
Ese valor es el que habría que usar como valor de incremento en cada pulso de reloj para que en el bit más significativo del registro de 54 bits (bit 53) tengamos una señal a 87.5 MHz. Nótese que para valores de incremento que no sean potencias de 2, obtendremos señales no cuadradas o de fase algo irregular (en el anterior post dedicado a la transmisión FM se profundiza en este tema), pero para el caso que nos ocupa, la "calidad" de la señal resultante no es significativa, lo importante es que la frecuencia fundamental sea la correcta. Para hacer modulación en frecuencia hemos de modificar esta frecuencia en el rango de -75 KHz y +75 KHz, lo que nos genera los siguiente incrementos mínimos y máximos:
$$ I_{min} = {(87500000 - 75000) \over 300000000} \times 2^{54} = 5249695965638208 $$
$$ I_{max} = {(87500000 + 75000) \over 300000000} \times 2^{54} = 5258703164892949 $$
Si calculamos la diferencia entre los incrementos y la dividimos entre dos nos dará el valor 4503599627370.5 que es la amplitud máxima que deberá tener la señal del ADC para que modifique el valor del incremento y que este, a su vez, genere una variación máxima de +- 75 KHz en la frecuencia portadora.
Como la salida del ADC da valores entre -8191 y +8191 a este valor hay que multiplicarle el valor ${4503599627370.5 \over 8191} = 549822930$ para que valores próximos a -8191 en la salida del ADC generen una portadora de 87.5 MHz - 75 KHz = 87.425 MHz y valores próximos a +8191 en la salida del ADC generen una portadora de 87.5 MHz + 75 KHz = 87.575 MHz. El valor del incremento del acumulador de fase que genera la señal de la antena será el siguiente:
$$ I = I_{central} + (ADC \times 549822930) = 5254199565265579 + (ADC \times 549822930) $$
A continuación puede verse el código fuente completo (cabe en un único fichero VHDL).
library ieee; use ieee.std_logic_1164.all; use ieee.numeric_std.all; entity MAX10FMTransmitter is port ( Clk : in std_logic; AnalogComparator : in std_logic; PWM : out std_logic; Antenna : out std_logic; Led : out std_logic_vector(7 downto 0) ); end entity; architecture A of MAX10FMTransmitter is component PLL port ( inclk0 : in std_logic := '0'; c0 : out std_logic ); end component; signal Clk300 : std_logic; signal ADCFollowerD : std_logic; signal ADCFollowerQ : std_logic; signal ADCScalerD : std_logic_vector(12 downto 0); signal ADCScalerQ : std_logic_vector(12 downto 0); signal ADCAccumulatorD : std_logic_vector(13 downto 0); signal ADCAccumulatorQ : std_logic_vector(13 downto 0); -- signed value: -8191 to +8191 signal ADCOutputD : std_logic_vector(13 downto 0); signal ADCOutputQ : std_logic_vector(13 downto 0); signal PhaseAccumulatorD : std_logic_vector(53 downto 0); signal PhaseAccumulatorQ : std_logic_vector(53 downto 0); signal PhaseAccumulatorIncD : std_logic_vector(53 downto 0); signal PhaseAccumulatorIncQ : std_logic_vector(53 downto 0); -- increment for phase accumulator to transmit at 87.5 MHz: (87500000 / 300000000) * (2^54) = 5254199565265579 --constant TxCentralFrequencyInc : integer := 5254199565265579; -- must fit in 54 bits constant TxCentralFrequencyIncL : integer := 2863311531; -- 32 bits constant TxCentralFrequencyIncH : integer := 1223338; -- 22 bits constant TXCentralFrequencyInc : signed(53 downto 0) := to_signed(TxCentralFrequencyIncH, 22) & to_signed(TxCentralFrequencyIncL, 32); -- gain for ADC output constant ADCGain : integer := 549822930; -- ADCGain needs 30 bits begin -- PLL to obtain 300 MHz from external 12 MHz P : PLL port map ( inclk0 => Clk, c0 => Clk300 ); -- ADC process (Clk300) begin if (Clk300'event and (Clk300 = '1')) then ADCFollowerQ <= ADCFollowerD; end if; end process; ADCFollowerD <= AnalogComparator; PWM <= ADCFollowerQ; process (Clk300) begin if (Clk300'event and (Clk300 = '1')) then ADCScalerQ <= ADCScalerD; end if; end process; ADCScalerD <= std_logic_vector(unsigned(ADCScalerQ) + 1); process (Clk300) begin if (Clk300'event and (Clk300 = '1')) then ADCAccumulatorQ <= ADCAccumulatorD; end if; end process; ADCAccumulatorD <= std_logic_vector(to_signed(0, 14)) when (unsigned(ADCScalerQ) = 0) else std_logic_vector(signed(ADCAccumulatorQ) + to_signed(1, 14)) when (ADCFollowerQ = '1') else std_logic_vector(signed(ADCAccumulatorQ) - to_signed(1, 14)) when (ADCFollowerQ = '0') else ADCAccumulatorQ; process (Clk300) begin if (Clk300'event and (Clk300 = '1')) then ADCOutputQ <= ADCOutputD; end if; end process; ADCOutputD <= ADCAccumulatorQ when (unsigned(ADCScalerQ) = 0) else ADCOutputQ; Led <= ADCOutputQ(13 downto 6); -- phase accumulator process (Clk300) begin if (Clk300'event and (Clk300 = '1')) then PhaseAccumulatorQ <= PhaseAccumulatorD; end if; end process; PhaseAccumulatorD <= std_logic_vector(unsigned(PhaseAccumulatorQ) + unsigned(PhaseAccumulatorIncQ)); Antenna <= PhaseAccumulatorQ(53); -- phase accumulator increment control (output frequency control) process (Clk300) begin if (Clk300'event and (Clk300 = '1')) then PhaseAccumulatorIncQ <= PhaseAccumulatorIncD; end if; end process; -- 14 bits * 40 bits = 54 bits PhaseAccumulatorIncD <= std_logic_vector((signed(ADCAccumulatorQ) * to_signed(ADCGain, 40)) + TxCentralFrequencyInc) when (unsigned(ADCScalerQ) = 0) else PhaseAccumulatorIncQ; end architecture;
El bit 53 del registro acumulador de fase se saca por un pin de la FPGA y en dicho pin se puede colocar un simple trozo de cable. No es necesario hacer ningún circuito que acondicione la señal de salida.
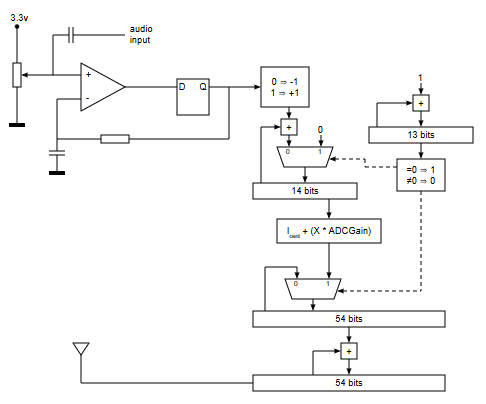
Si a corta distancia del circuito ponemos un receptor de radio FM comercial sintonizado a 87.5 MHz podremos escuchar la señal que está leyendo el ADC de la FPGA y que está siendo transmitida en FM.
Código fuente disponible en la sección soft.
[ añadir comentario ] ( 1754 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 2182 )
( 3 / 2182 )¿Se pueden generar efectos de sonido rudimentarios sin un chip de sonido y utilizando muy pocas macroceldas de un CPLD o una FPGA?
Motivación
En la anterior entrada del blog se realizó un pequeño proyecto para generar dos efectos de sonido utilizando un sencillo chip PSG, el SN76489. Los sonidos generados fueron muy buenos pero a nivel hardware, como el objetivo del montaje es una futura integración en un pequeño robot con mando a distancia, me encontré con que, el hecho de tener que cablear todo un bus de 8 bits junto con los pines OE y READY, consumía muchos pines del STM32 (el robot consume ya GPIO y PWM para las ruedas, UART para la comunicación e I2C para una pequeña pantalla OLED).
Una primera aproximación válida sería un conversor serie a paralelo de tipo I2C o algo así pero instalar DOS chips sólo para generar dos ruidos rudimentarios me pareció excesivo, por lo que opté por una solución basada en un CPLD.
64 macroceldas
Ese es el reto: hacer un generador de sonido que consuma, como mucho, 64 macroceldas en un CPLD de la serie MAX3000A de Intel, en concreto el EPM3064.

64 macroceldas son 64 biestables con la lógica combinatoria asociada. No es un reto sencillo y es probable que los resultados no tengan tan buena calidad como con un PSG, pero el beneficio que se consigue en reducción de pines, miniaturización y reducción de consumo (Un CPLD consume mucho para los estándares actuales, pero el SN76489 consume más) hace que valga la pena intentarlo.
El circuito
Se plantea un circuito sencillo con dos entradas configuradas en lógica negativa y circuitería antirrebote básica y una salida con condensador de desacoplo y divisor de tensión para evitar sobretensiones en el amplificador de audio de la salida. La placa equipada con el CPLD EPM3064 incluye un oscilador a 50 MHz conectado a uno de los pines de reloj del CPLD y un led con su cátodo conectado a otro de los pines del CPLD (se enciende cuando se emite un 0 por ese pin).
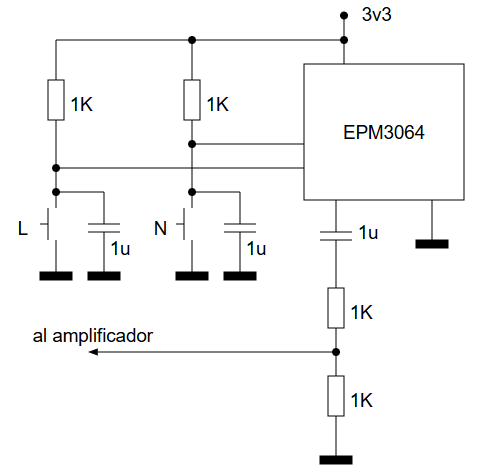
Diagrama de bloques
A continuación puede verse el diagrama del bloques que se ha implementado en el CPLD.
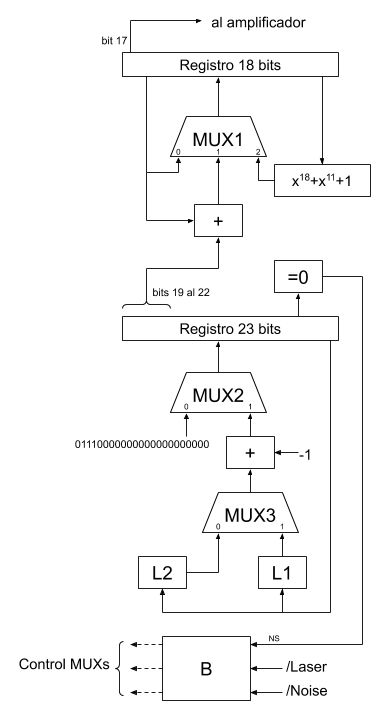
El bloque $x^{18} + x^{11} + 1$ se corresponde con el LFSR maximal de grado 18 que permite generar ruido blanco (aproximado) en el registro de arriba.
L1 es un bloque combinacional que emite un 1 si la entrada vale 0 y la entrada sin cambiar en caso contrario.
| L1 | |
|---|---|
| Entrada | Salida |
| 0 | 1 |
| x | x |
L2 es un bloque combinacional que emite 8193 si la entrada vale 0 y la entrada sin cambiar en caso contrario.
| L2 | |
|---|---|
| Entrada | Salida |
| 0 | 8193 |
| x | x |
B es el bloque combinacional encargado de controlar los multiplexores en función de las señales de entrada y del cruce por cero del registro de 23 bits:
| B | |||||
|---|---|---|---|---|---|
| Entradas | Salidas (MUX) | ||||
| /Laser | /Noise | NS | 1 | 2 | 3 |
| 1 | 1 | dc | 1 | 1 | 1 |
| 0 | dc | dc | 0 | 0 | dc |
| 1 | 0 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 2 | 1 | 0 |
Descripción funcional
Cuando se activa la entrada /Laser (se pone a nivel bajo), se carga en el registro de 23 bits el valor "01110000000000000000000", este valor se carga para que los 4 bits más significativos tengan el valor "0111". Si nos fijamos los 4 bits más significativos del registro de 23 bits se utlizan para incrementar el valor del registro de 18 bits. Dicho registro de 18 bits actúa como acumulador de fase para una señal de onda cuadrada correspondiente al bit más significativo (bit 17) de este registro.
Si tenemos un registro de 18 bits como acumulador de fase y una frecuencia de reloj de 50 MHz (la de la placa que estamos usando) tendremos una frecuencia del bit más significativo de:
$$f_{out} = {f_{clk} \over 2^{18}}$$
De forma general, en caso de que apliquemos incrementos arbitrarios a este registro de desplazamiento, obtendremos una frecuencia en el bit más significativo de:
$$f_{out} = Inc \times {f_{clk} \over 2^{18}} = Inc \times {50000000 \over 2^{18}}$$
Para simular el sonido de un disparo láser lo que generamos es una caida rápida en frecuencia por lo que empezamos con un $Inc = 7$ cuando /Laser = 0 (de ahí los 4 bits más significativos del valor 01110000000000000000000), este valor de incremento genera una frecuencia en el bit más significativo del registro de 18 bits de:
$$Inc = 7 \Rightarrow f_{out} = 7 \times {50000000 \over 2^{18}} = 1335.1 Hz$$
Cuando /Laser vuelve al valor 1, vamos bajando el valor de Inc (los 4 bits más significativos del registro de 23 bits) hasta que vale 0:
$$Inc = 6 \Rightarrow f_{out} = 1144.4 Hz$$
$$Inc = 5 \Rightarrow f_{out} = 953.67 Hz$$
$$Inc = 4 \Rightarrow f_{out} = 762.94 Hz$$
$$Inc = 3 \Rightarrow f_{out} = 572.2 Hz$$
$$Inc = 2 \Rightarrow f_{out} = 381.47 Hz$$
$$Inc = 1 \Rightarrow f_{out} = 190.73 Hz$$
$$Inc = 0 \Rightarrow f_{out} = 0 Hz$$
Como el registro de 23 bits también actúa como un acumulador de fase (pues se decrementa en bloque, no solo los bits más significativos), la caida es lo suficientemente lenta como para ser audible (que es lo que queremos). Nótese que una vez cae a 0, el registro de 23 bits se queda ahí estancado gracias al circuito combinacional L1 que actúa como limitador, lo que, en la práctica, provoca que el registro de 18 bits "pare" de oscilar (pues $Inc = 0$ siempre). Nótese también que, aunque pare de oscilar, es posible que a la salida que va hacia el amplificador (el bit 17) se quede un "1" de forma pemanente, es por ello por lo que se hace necesario colocar siempre un condensador de desacoplo a la salida.
Si lo que se pone a 0 es la entrada /Noise y la entrada /Laser permanece a 1, lo que se hace es seleccionar como realimentación del registro de 18 bits la salida del polinomio LFSR, que provocará una secuencia de números pseudoaleatorios (ruido) en el bit 17 (salida del amplificador). La carga del valor del LFSR no se produce en cada ciclo del reloj de 50 MHz, pues provocaría ruido no audible, sino que se aprovecha el registro de desplazamiento de 23 bits y, a través del circuito combinacional L2, se hace que "desborde" en 8192, por lo que el registro de 18 bits cambiará con una frecuencia de:
$$f_{muestreo} = {50000000 \over 8192} = 6103.5 Hz$$
por lo que el ruido resultante ocupará aproximadamente hasta la banda de los 3 KHz. No es un ruido blanco pero a efectos audibles es muy parecido al ruido generado por un PSG.
Código fuente
Todo el código fuente en VHDL puede meterse dentro de una sola entidad:
library ieee; use ieee.std_logic_1164.all; use ieee.numeric_std.all; entity Epm3064GunSound is port ( Clk : in std_logic; TrigLaserIn : in std_logic; TrigNoiseIn : in std_logic; SpeakerOut : out std_logic; LedOut : out std_logic ); end entity; architecture Architecture1 of Epm3064GunSound is signal LFSRD : std_logic_vector(17 downto 0); signal LFSRQ : std_logic_vector(17 downto 0); signal LFSRRawOut : std_logic_vector(17 downto 0); signal LFSROut : std_logic_vector(17 downto 0); signal LFSRMux : std_logic_vector(1 downto 0); signal TimerD : std_logic_vector(22 downto 0); signal TimerQ : std_logic_vector(22 downto 0); signal TimerMux : std_logic; signal Limited1TimerQ : std_logic_vector(22 downto 0); signal Limited2TimerQ : std_logic_vector(22 downto 0); signal LimiterMux : std_logic; signal LimiterMuxOut : std_logic_vector(22 downto 0); signal NoiseSample : std_logic; begin -- LFSR process (Clk) begin if (Clk'event and (Clk = '1')) then LFSRQ <= LFSRD; end if; end process; --LFSRRawOut <= (LFSRQ(0) xor LFSRQ(3)) & LFSRQ(19 downto 1); 20 bits LFSRRawOut <= (LFSRQ(0) xor LFSRQ(7)) & LFSRQ(17 downto 1); -- 18 bits LFSROut <= LFSRRawOut when (unsigned(LFSRRawOut) /= 0) else std_logic_vector(to_unsigned(1, 18)); LFSRD <= LFSROut when (LFSRMux = "10") else std_logic_vector(unsigned(LFSRQ) + unsigned(TimerQ(22 downto 19))) when (LFSRMux = "01") else LFSRQ; SpeakerOut <= LFSRQ(17); -- timer process (Clk) begin if (Clk'event and (Clk = '1')) then TimerQ <= TimerD; end if; end process; Limited1TimerQ <= std_logic_vector(to_unsigned(1, 23)) when (signed(TimerQ) = 0) else TimerQ; Limited2TimerQ <= std_logic_vector(to_unsigned(8192 + 1, 23)) when (signed(TimerQ) = 0) else TimerQ; LimiterMuxOut <= Limited1TimerQ when (LimiterMux = '1') else Limited2TimerQ; TimerD <= std_logic_vector(signed(LimiterMuxOut) - 1) when (TimerMux = '1') else "01110000000000000000000"; NoiseSample <= '1' when (signed(TimerQ) = 0) else '0'; -- operation logic LFSRMux <= "01" when (((TrigLaserIn = '1') and (TrigNoiseIn = '1')) or (TrigLaserIn = '0')) else "10" when ((TrigLaserIn = '1') and (TrigNoiseIn = '0') and (NoiseSample = '1')) else "00"; TimerMux <= '0' when (TrigLaserIn = '0') else '1'; LimiterMux <= '1' when ((TrigLaserIn = '1') and (TrigNoiseIn = '1')) else '0'; LedOut <= TrigLaserIn and TrigNoiseIn; end architecture;
Resultados
Con este circuito se consiguen unos resultados similares a los obtenidos utilizando el chip SN76489, con menos circuitería, ocupando menos pines y menos tiempo de procesamiento en el microcontrolador: nótense que ahora sólo necesitamos dos pines GPIO del microcontrolador (uno para /Laser y otro para /Noise).
Todo el código fuente puede descargarse de la sección soft.
[ añadir comentario ] ( 1869 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 2438 )
( 3 / 2438 )
 Calendario
Calendario




