Los fundamentos
La modulación FM consiste en hacer variar la frecuencia de la señal que estamos mandando a la antena en función de la amplitud de la señal moduladora (sonido, por ejemplo). El rango de frecuencias reservado para emisoras comerciales de audio abarca desde los 87.5 MHz hasta los 108 MHz (es el rango que recoge cualquier receptor FM analógico) con una profundidad de modulación de +- 75 KHz. Esto significa que si queremos emitir en la frecuencia de 100 MHz debemos hacer variar la frecuencia entre 99.925 MHz y 100.075 MHz en función de la amplitud de la señal moduladora.
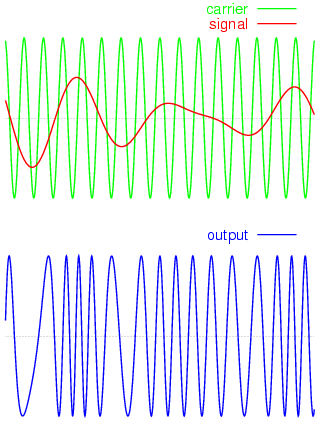
(imagen extraida de Wikipedia, con licencia Creative Commons Attribution - Share Alike 2.0, autor Gvf)
Generar la señal en el dominio digital
Intentar hacer un transmisor FM utilizando una FPGA nos hace chocar, a priori, con un primer impedimento: Poder generar una señal que varíe de frecuencia de una forma tan ligera. Hay que tener en cuenta que con una anchura de modulación de 150 KHz (75 KHz + 75 KHz) y asumiendo una señal sonora muestreada a 16 bits tenemos que la variación de la señal de salida de la antena debe de ser en pasos de:
$${150000 \over {2^{16}}} = {150000 \over 65536} = 2.2888 Hz$$
Esos son muy pocos hercios. En el dominio digital lo habitual para modificar la frecuencia de una señal es multiplicarla por una constante (mediante un PLL) o dividirla entre una constante (mediante un divisor de frecuencias). Los PLLs son circuitos híbridos (entre analógicos y digitales), no son todo lo rápido que nos gustaría (lo normal es que un PLL necesite varios ciclos hasta estabilizarse en la frecuencia deseada), normalmente trabajan con factores constantes (no variables como en nuestro caso) y no están siempre disponibles en las FPGAs para uso directo del usuario. Los divisores de frecuencia son más fáciles de hacer (no dejan de ser baterías de biestables) pero, como su propio nombre indica, sólo son capaces de dividir la frecuencia entre un valor entero.
Acumuladores de fase
Existe, sin embargo, una forma bastante ingeniosa para la síntesis directa de señales digitales sin necesidad del uso de PLLs ni de divisores de frecuencia: los acumuladores de fase. Un acumulador de fase es una de las partes que integran un oscilador digital basado en tabla de ondas. Imaginemos que queremos generar una onda senoidal mediante una tabla de ondas.
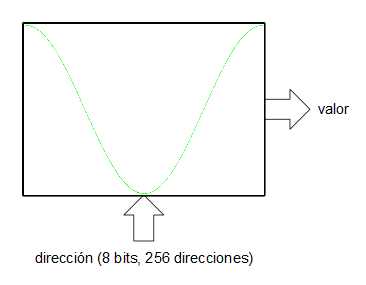
Asumiremos, por simplificar, que la tabla de la onda (realmente sería una ROM o una RAM) tiene un tamaño de 256 muestras ($2^8$). Por otro lado tenemos un registro (al que llamaremos acumulador de fase) de 16 bits y lo que hacemos es indexar la tabla de ondas utilizando los 8 bits más significativos del acumulador de fase. Las entradas D de los biestables de este registro se conectan a la salida un sumador que suma las salidas Q (el valor actual de registro) más un valor de entrada de 16 bits. En cada flanco de subida del reloj del sistema el registro (el acumulador de fase) se carga con el valor de las entradas D procedentes del sumador. En cada tick de reloj el acumulador va acumulando el valor de la entrada de 16 bits.
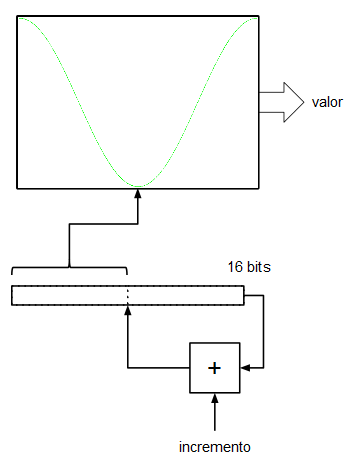
Si en la entrada de 16 bits ponemos un 0, el registro se quedará "quieto", no cambiará su valor y, por tanto la salida de datos de la ROM indexada por dicho registro sacará un valor constante (frecuencia de 0 Hz). Si en la entrada de 16 bits ponemos un 1, en registro se irá incrementando de 1 en 1, sin embargo, como lo que indexa a la tabla de valores son los 8 bits más significativos, este índice sólo avanzará cada 256 pulsos de reloj del sistema. Esto significa que con una frecuencia de reloj de 32 KHz, nuestro oscilador generaría una señal con una frecuencia de:
$${32000 \over 256} = 125 Hz$$
Yéndonos al otro extremo, si en la entrada de 16 bits metemos un valor de $2^{15} = 32768$, el acumulador de fase, al ser de 16 bits, se desbordará cada dos ciclos de reloj: el acumulador de fase generará la secuencia de valores 0, 32768, 0, 32768, 0, 32768, etc. que, a su vez, indexarán los valores mínimo y máximo de la onda senoidal que tenemos en la tabla. Esto significa que la salida del oscilador ha alcanzado su frecuencia máxima (su frecuencia de Nyquist, de 16 KHz).
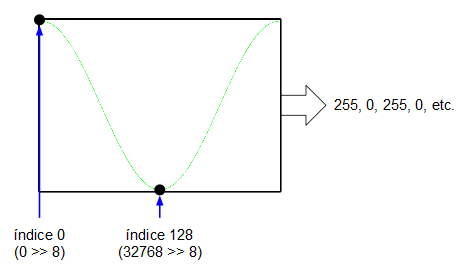
Como se puede comprobar, los incrementos en los pasos son lineales por lo que podemos establecer una especie de regla de tres para el cálculo de la frecuencia de salida de nuestro oscilador imaginario:
$$I_{acumulador fase} = {f_{deseada} \over 32000} \times 2^{16}$$
Vemos que si frecuencia_deseada = 0, entonces incremento_acumulador_fase = 0. Si frecuencia_deseada = 16000 (la frecuencia Nyquist, para 32 KHz), entonces:
$$I_{acumulador fase} = {16000 \over 32000} \times 2^{16} = {1 \over 2} \times 2^{16} = 2^{15} = 32768$$
Para 440 Hz (la nota LA de la cuarta octava del piano) tenemos que:
$$I_{acumulador fase} = {440 \over 32000} \times 2^{16} = 901.12$$
En estos casos, cuando el resultado es fraccionario, hay dos opciones: O quedarse con la parte entera (redondeando o truncando, incremento_acumulador_fase = 901), o, si no queremos perder precisión, incrementar el número de bits para reducir el error. Por ejemplo, utilizando un acumulador de fase de 59 bits conseguiríamos un valor de incremento entero (sin parte fraccionaria):
$$I_{acumulador fase} = {440 \over 32000} \times 2^{59} = 7926335344172073$$
De forma general se puede plantear la ecuación de la siguiente manera:
$$I_{acumulador fase} = {f_{deseada} \over f_{muestreo}} \times 2^{bits}$$
Nótese que la cantidad de bits que indexa la tabla de ondas no es relevante. Lo único importante es que la tabla de ondas está indexada por la parte alta del registro acumulador de fase. Como se puede apreciar, con este método es posible generar frecuencias arbitrarias con pasos relativamente pequeños y sólo limitados por el número de bits que utilicemos en el acumulador de fase.
El transmisor
Imaginemos que la frecuencia de muestreo es ahora de 320 MHz y que queremos generar una frecuencia de 100 MHz. Utilizando un acumulador de fase de 32 bits (la cantidad de bits elegida es arbitraria) tendríamos que:
$$I_{acumulador fase} = {100000000 \over 320000000} \times 2^{32} = 1342177280$$
Como se comentó antes, la cantidad de bits de resolución a la hora de indexar la tabla de ondas no es relevante a efectos de frecuencia (aunque sí a efectos de distorsión armónica y de relación señal/ruido). En nuestro caso, como no disponemos de un DAC sino que vamos a generar una señal cuadrada directamente, en teoría lo que necesitamos es una tabla con una onda cuadrada de tal forma que cuando esté en el máximo emita un 1 y cuando esté en el mínimo emita un 0.
Si asumimos que en la tabla de ondas vamos a meter una onda cuadrada con un ciclo de trabajo del 50% (perfectamente cuadrada), esto significará que la mitad de la tabla de ondas va a estar al valor mínimo (0 por ejemplo) y la otra mitad al valor máximo (255 por ejemplo, si es una ROM de 8 bits sin signo). Si al final vamos a traducir la salida de la tabla de ondas como un 0 si está en el valor mínimo y como un 1 si está en el valor máximo, es obvio que la salida de la tabla de ondas coincidirá con el valor del bit más significativo del acumulador de fase.
Y he aquí la "magia" del invento: Usando un único registro con un sumador podemos hacer un oscilador de onda cuadrada para el que podemos controlar la frecuencia de forma precisa entre 0 Hz y la mitad de la frecuencia de reloj. La precisión a la hora de ajustar la frecuencia nos la dará la cantidad de bits que usemos.
El jittering
Cualquier incremento en el acumulador de fase que no sea potencia de dos va a generar un efecto jitter en la señal de salida haciendo que ésta muchas veces diste de ser una señal cuadrada perfecta. Esto, como es obvio, provocará que la cantidad de armónicos que se generen se dispare. Vamos a verlo con un ejemplo.
Imaginemos el caso anterior: 320 MHz de frecuencia de reloj, un acumulador de fase de 32 bits y un incremento para el acumulador de fase igual a 1342177280. Aplicando este acumulador de fase obtenemos la siguiente salida (correspondiente al bit más significativo):
1 1 0 1 1 0 1 1 0 0 1 0 0 1 0 0 ... la secuencia se repite indefinidamente
Como se puede observar esta secuencia de bits dista mucho de parecerse a una señal cuadrada con ciclo de trabajo del 50%, en concreto genera tres pulsos anchos más juntos y luego dos pulsos estrechos más separados. Sin embargo si hacemos el análisis de Fourier de esta secuencia, tratándola como si fuese una señal, calculándole la transformada de Fourier usando un software numérico como Octave:
octave> abs(fft([1 1 0 1 1 0 1 1 0 0 1 0 0 1 0 0])) ans = 8.00000 1.79995 0.00000 1.01959 0.00000 5.12583 0.00000 1.20269 0.00000 1.20269 0.00000 5.12583 0.00000 1.01959 0.00000 1.79995
Vemos que la transformada de Fourier resultante es efectivamente simétrica (quitando la posición 0, que es la componente de continua), al tratarse de una señal real, y que, descartando la componente de continua (el índice 0 del vector), hay un máximo en el índice 5 del vector. Por las propiedades de la transformada de Fourier en este caso la posición 8 (el centro del vector y el centro de simetría) se corresponde con la frecuencia Nyquist que, al ser la frecuencia de reloj de 320 MHz, sería de 160 MHz (la mitad de la frecuencia del reloj). El máximo situado en la posición 5 del vector se corresponderá, siguiendo una regla de tres, con la frecuencia de:
$${{160000000 \times 5} \over 8} = 100000000 = 100 MHz$$
En efecto, la frecuencia fundamental (el máximo en la transformada de Fourier) de la señal de salida es de 100 MHz, que era nuestro objetivo, aunque como se puede ver en el análisis de Fourier, también se emitirán armónicos de 20 MHz (el valor 1.79995 se corresponde con la frecuencia ${{160 \times 1} \over 8}$), de 60 MHz (${{160 \times 3} \over 8}$) y de 140 MHz (${{160 \times 7} \over 8}$), aunque de menor amplitud.
Implementación y prueba de concepto
Como se va a emitir el sonido por radio FM y aún no disponemos de un ADC que permita la lectura de una fuente externa de audio, se generará la señal de audio dentro de la propia FPGA.
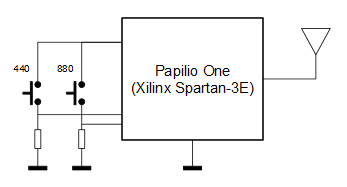
El sistema consta de dos entradas conectadas a sendos botones y que permiten seleccionar la frecuencia del tono a transmitir: cuando no se pulsa ningún botón no se modula (se genera la portadora sin modular), cuando se pulsa el botón “440” la portadora se modula con una señal cuadrada de 440 Hz (nota LA en la cuarta octava del piano), mientras que si se pulsa el botón “880” la portadora se modula con una señal cuadrada de 880 Hz (nota LA en la quinta octava del piano).
La única salida del sistema es la salida de la antena, que va a un trozo de cable que se coloca al aire. No es necesario nada más si vamos a colocar el receptor a pocos metros de la FPGA. En el caso de que queramos conectar la salida a una antena real y que queramos más potencia habría que colocar circuitos acondicionadores y/o amplificadores a la salida y, sobretodo, filtros: hay que recordar que la señal de salida es una onda cuadrada repleta de armónicos.
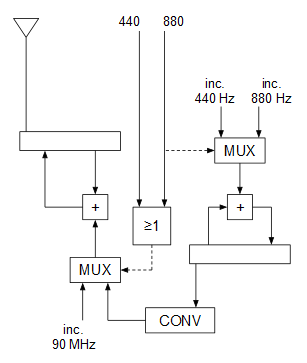
En reposo, las entradas “440” y “880” valen 0, por lo que el MUX inferior selecciona la entrada del incremento correspondiente a los 90 MHz (portadora sin modular). Cuando se pulsa sólo el botón “440” el MUX inferior deja pasar la señal moduladora (ya convertida en secuencias de incrementos en lugar de en 0 y 1) a la entrada del oscilador para modularlo, y cuando se pulsa el botón “880” ocurre lo mismo con el MUX inferior y, además, al cambiar la entrada de selección del MUX superior, cambia el incremento del oscilador que genera la señal moduladora para que genere 880 Hz en lugar de 440 Hz.
El módulo combinacional CONV convierte la entrada de 1 bit (0 o 1) proveniente del oscilador de 440 u 880 Hz, en una salida de 32 bits que es el incremento de fase de correspondiente a cada nivel de la señal moduladora:
0 --> 1341058799
1 --> 1343295761
En este caso se ha realizado una implementación sobre una FPGA Spartan-3E de Xilinx con un reloj externo de 32 MHz (papilio one). Las Spartan-3E disponen de varios DCM (Digital Clock Managers) que permiten subir la frecuencia de reloj mediante multiplicadores. En este caso, con un reloj a 32 MHz la máxima frecuencia que se puede alcanzar es de 288 MHz, por lo que ajustamos los cálculos a dicha frecuencia y asumiendo que vamos a transmitir en la banda de 90 MHz.
$$I_{acumulador fase} = {90000000 \over 288000000} \times 2^{32} = 1342177280$$
Como la señal moduladora (los tonos de 440 y 880 Hz) van a ser también ondas cuadradas, sólo hay que calcular los incrementos para el 0 y el 1 de la señal moduladora (en este caso no hay valores intermedios). El 0 de la señal moduladora lo asociaremos a 89,925 MHz y el 1 de la señal moduladora lo asociaremos a 90,075 MHz (recordemos que la profundidad de modulación en la FM comercial es de 75 KHz).
$$I_{89.925} = {89925000 \over 288000000} \times 2^{32} \approx 1341058799$$
$$I_{90.075} = {90075000 \over 288000000} \times 2^{32} \approx 1343295761$$
A continuación puede verse el código fuente:
library ieee; use ieee.std_logic_1164.all; use ieee.numeric_std.all; entity FMTransmitter is port ( Clk : in std_logic; Reset : in std_logic; Button440 : in std_logic; Button880 : in std_logic; AntOut : out std_logic ); end entity; architecture Architecture1 of FMTransmitter is component Oscillator is generic ( NBits : integer := 32 ); port ( IncrementIn : in std_logic_vector(31 downto 0); Clk : in std_logic; Reset : in std_logic; DataOut : out std_logic ); end component; component Mux2Inputs is generic ( NBits : integer := 32 ); port ( Sel : in std_logic; DataIn0 : in std_logic_vector((NBits - 1) downto 0); DataIn1 : in std_logic_vector((NBits - 1) downto 0); DataOut : out std_logic_vector((NBits - 1) downto 0) ); end component; signal Mux1Out : std_logic_vector(31 downto 0); signal Mux1Sel : std_logic; signal ConvOut : std_logic_vector(31 downto 0); signal ConvIn : std_logic; signal Mux2Out : std_logic_vector(31 downto 0); begin RadioOsc : Oscillator generic map ( NBits => 32 ) port map ( Clk => Clk, Reset => Reset, IncrementIn => Mux1Out, DataOut => AntOut ); Mux1Sel <= Button440 or Button880; Mux1 : Mux2Inputs generic map ( NBits => 32 ) port map ( Sel => Mux1Sel, DataIn0 => std_logic_vector(to_unsigned(1342177280, 32)), -- center freq = 90.0 MHz DataIn1 => ConvOut, DataOut => Mux1Out ); -- center freq - 75 KHz when 0 -- center freq + 75 KHz when 1 ConvOut <= std_logic_vector(to_unsigned(1341058799, 32)) when (ConvIn = '0') else std_logic_vector(to_unsigned(1343295761, 32)); AudioOsc : Oscillator generic map ( NBits => 32 ) port map ( Clk => Clk, Reset => Reset, IncrementIn => Mux2Out, DataOut => ConvIn ); Mux2 : Mux2Inputs generic map ( NBits => 32 ) port map ( Sel => Button880, DataIn0 => std_logic_vector(to_unsigned(6562, 32)), -- 440 Hz DataIn1 => std_logic_vector(to_unsigned(13124, 32)), -- 880 Hz DataOut => Mux2Out ); end architecture;
Tanto el oscilador de salida (el de alta frecuencia) como el oscilador de audio se han implementado usando el mismo componente “Oscillator.vhd”.
library ieee; use ieee.std_logic_1164.all; use ieee.numeric_std.all; use ieee.std_logic_signed.all; entity Oscillator is generic ( NBits : integer := 32 ); port ( IncrementIn : in std_logic_vector(31 downto 0); Clk : in std_logic; Reset : in std_logic; DataOut : out std_logic ); end entity; architecture Architecture1 of Oscillator is component Reg is generic ( NBits : integer := 32 ); port ( Enable : in std_logic; Clk : in std_logic; DataIn : in std_logic_vector((NBits - 1) downto 0); DataOut : out std_logic_vector((NBits - 1) downto 0) ); end component; signal MuxOut : std_logic_vector((NBits - 1) downto 0); signal RegOut : std_logic_vector((NBits - 1) downto 0); begin PhaseAcc : Reg generic map ( NBits => NBits ) port map ( Enable => '1', Clk => Clk, DataIn => MuxOut, DataOut => RegOut ); MuxOut <= (others => '0') when (Reset = '1') else (RegOut + IncrementIn); DataOut <= RegOut(NBits - 1); end architecture;
El tipo de sumador
En otros proyectos FPGA anteriormente abordados en este blog, cada vez que hacía falta un sumador se tiraba de un sumador estándar implementado mediante lógica combinatoria (“Adder.vhd”). Hasta ahora se ha hecho así por razones pedagógicas. En este caso, sin embargo, al estar el reloj a una frecuencia extremadamente alta para la FGPA ha sido necesario el uso del operador “+”. Este operador garantiza “la mejor implementación” de la suma para la plataforma y esto se traduce, en el caso del Spartan-3E y en el caso de la mayoría de las FPGAs existentes, en que se va a hacer uso de sumadores que ya se encuentran integrados (“hardwired”) en el sustrato de todas las FPGA (todos los fabricantes los incluyen, de mayor o menor cantidad de bits).
¿Qué ventajas tienen estos sumadores con respecto al sumador que hemos estado usando hasta ahora? La principal diferencia es que en nuestro “Adder.vhd” el acarreo es en cascada, mientras que los sumadores implementados a fuego en las FPGAs están basados siempre en circuitos CLA (Carry Look Ahead), que permiten precalcular los acarreos de cada bit sin necesidad de que estén calculados los bits anteriores. Aún siendo circuitos combinacionales tanto los unos como los otros, el tiempo de propagación del resultado en el caso de sumadores con CLA es mucho menor que en el caso de sumadores con acarreo en cascada (como el “Adder.vhd” que hemos usado hasta ahora en los proyectos).
En nuestro caso concreto se da además la circunstancia que, con un reloj a 288 MHz, el sumador con acarreo en cascada (el “Adder.vhd” de siempre) da problemas de timing o, lo que es lo mismo, “no le da tiempo de sumar tan rápido” y no queda otra opción que tirar del operador “+” (cosa que, por otro lado, es lo recomendable ya que se garantiza siempre la mejor implementación).
Vídeo
A continuación un pequeño fragmento de vídeo donde se puede ver y escuchar el invento en funcionamiento. La calidad del audio es bastante baja: usé mi radio-despertador como receptor, en el receptor del móvil se oye mucho mejor… pero no hubiese podido grabarlo :-)
Espero que haya resultado interesante. Todo el código fuente se puede descargar de la sección soft.
[ añadir comentario ] ( 3400 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 5922 )
( 3 / 5922 )
 Calendario
Calendario




