Conversión analógica digital delta-sigma
Como se puede comprobar en el post anterior relacionado, la conversión analógica digital de tipo delta-sigma tiene la ventaja de requerir muy pocos componentes externos: un comparador analógico (para lo que puede usarse un amplificador operacional normal), un condensador y una resistencia; y permite implementar un ADC de precisión arbitraria (la precisión sólo está limitada por los recursos disponibles en la FPGA).
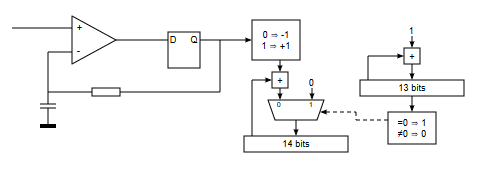
Recordemos que la conversión analógico digital de tipo delta-sigma lo que hace es, mediante un biestable de tipo D, hacer que la salida que carga el condensador C a través de la resistencia R "siga" a la entrada analógica:
- Si la entrada + del comparador está por encima de la entrada -, el comparador emite un 1, que es cargado en el siguiente ciclo de reloj por el biestable de entrada, haciendo que la salida que va a la resistencia R tome el valor de 1 y trate de "acercar" el valor de la entrada - del comparador al valor de la entrada + del comparador.
- Si la entrada + del comparador está por debajo de la entrada -, el comparador emite un 0, que es cargado en el siguiente ciclo de reloj por el biestable de entrada, haciendo que la salida que va a la resistencia R tome el valor de 0 y trate de "acercar" (esta vez hacia "abajo") el valor de la entrada - del comparador al valor de la entrada + del comparador.
Como se puede ver, este comportamiento hace que para valores próximos a 0 voltios en la entrada + del comparador, el biestable de entrada emite muchos más 0s que 1s, mientras que para valores próximos a 3.3 voltios en la entrada + del comparador, el biestable de entrada emite muchos más 1s que 0s. También se puede ver que para valores próximos a Vcc / 2 = 1.65 voltios, el biestable emitirá una cantidad aproximadamente igual de 0s que de 1s.
Si lo que hacemos ahora es asociar al valor 0 de la salida del biestable, el valor numérico -1, y, al valor 1 de la salida del biestable, el valor numérico +1, lo que tenemos es un circuito digital que emitirá:
- Más +1 que -1 para valores próximos a 3.3 voltios.
- Más -1 que +1 para valores próximos a 0 voltios.
- Una cantidad aproximadamente igual de -1 y +1 para valores próximos a 1.65 voltios.
Si vamos acumulando estos -1 y +1 sobre un acumulador que se pone a cero cada cierto tiempo, lo que tendremos es que en dicho acumulador tendremos un valor proporcional al voltaje de entrada del ADC:
- Valores próximos a 3.3 voltios, al generar más +1 que -1, dan como resultado un valor de conversión muy alto y positivo.
- Valores próximos a 0 voltios, al generar más -1 que +1, dan como resultado un valor de conversión muy bajo y negativo.
- Valores próximos a 1.65 voltios, al generar una cantidad aproximadamente similar de -1 y de +1, dan como resultado un valor de conversión próximo a 0.
Debido a esta necesidad de contar -1s y +1s necesitamos sobremuestreo: Si queremos obtener una resolución de 16 bits, eso significa que el valor máximo de conversión tendrá que ser -32767 mientras que el valor mínimo de conversión tendrá que ser -32768. Si asumimos una escala simétrica tendremos un valor entre -32767 y +32767, eso significa que debemos hacer 32767 sumas (de -1s y +1s) antes de leer el valor de conversión. Dichas sumas las tenemos que hacer en un registro, que llamaremos "acumulador de conversión".
Para el caso de 16 bits necesitaríamos un contador de 15 bits que, en el momento de que valga 0 haga que el "acumulador de conversión" copie su valor en el registro de salida del ADC y se ponga a cero, y, durante los 32767 pulsos restantes (hasta el siguiente desbordamiento), se sumen los -1s y +1s que van entrando.
Así vemos que, por ejemplo, para 12 MHz y 16 bits de resolución, como necesitaríamos un contador de 15 bits, al final la frecuencia de muestreo podrá ser, como máximo de:
$$ {12000000 \over {2^{15}}} = 366.21 \: Hz $$
Por ejemplo, si queremos hacer una conversión en calidad CD necesitaríamos un reloj de sistema (sobremuestreo) de:
$$ {44100 \times {2^{15}}} = 1445068800 \: Hz $$
En el caso que nos ocupa se ha decidido implementar el transmisor en una FPGA MAX10 de las que viene en una placa MAX1000 de Arrow, a 12 MHz, cuyo reloj puede ser subido mediante PLLs hasta unos 400 MHz. Debido a esta limitación se ha decidido subir el reloj a 300 MHz y, para trabajar con esa frecuencia de sobremuestreo, se han tenido que bajar un poco las especificaciones del ADC, usando un contador de 13 bits y un acumulador de conversión de 14 bits. De esta forma tenemos una frecuencia de muestreo de:
$$ {300000000 \over {2^{13}}} = 36621.09375 \: Hz $$
Por lo que el ancho de banda es de unos 18 KHz (buen ancho de banda para música) y la resolución de conversión es de 14 bits (valores de conversión entre -8191 y +8191). No es calidad CD pero tampoco está mal.
Consideraciones entorno a la entrada de sonido analógica
Hay que tener en cuenta que las señales de sonido tal cual salen de un amplificador, son señales simétricas (con semiciclos positivos y negativos) mientras que nuestro ADC mide voltajes entre 0 y 3.3 voltios (no mide voltajes negativos). Es necesario, por tanto, acondicional la señal de sonido de entrada para que quede "desplazada" hacia arriba y un valor de 0 voltios de entrada se traduzca en 1.65 voltios a la entrada + del comparador. Es por esto por lo que se coloca el divisor de tensión entre 3.3 y 0 voltios a la entrada de audio, que desplaza el "0" de la señal de sonido hasta los 1.65 voltios.
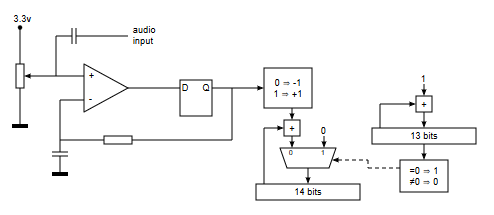
El nivel de señal que entrega la salida de auriculares de un ordenador es suficiente para la entrada del ADC y no requiere amplificación adicional, al menos para esta prueba.
Generador de señal de antena
La frecuencia de transmisión elegida es 87.5 MHz (el extremo inferior de la banda de radiodifusión de sonido). La señal de antena que se quiere generar debe estar centrada, por tanto, en dicha frecuencia y dicha frecuencia deberá variarse en un rango máximo de +-75 KHz (estándar de radiodifusión). Para la generación de frecuencias arbitrarias que sean inferiores a la frecuencia de reloj de un sistema digital lo lógico es utilizar un acumulador de fase.
Un acumulador de fase no es más que un registro que se incrementa en un valor constante (no tiene por qué incrementarse de 1 en 1) con desbordamiento. Por ejemplo, si a partir de un reloj de 300 MHz queremos generar un reloj de 75 MHz lo que podemos hacer es incrementar un registro de 2 bits de 1 en 1 a 300 MHz:
...
Pulso: 00 --> 01
Pulso: 01 --> 10
Pulso: 10 --> 11
Pulso: 11 --> 00
Pulso: 00 --> 01
Pulso: 01 --> 10
Pulso: 10 --> 11
Pulso: 11 --> 00
...
En este ejemplo se puede ver que si la frecuencia de pulso es de 300 MHz, la frecuencia del bit 0 será de ${300 \over 2} = 150 \: MHz$ mientras que la frecuencia del bit 1 será de ${150 \over 2} = 75 \: MHz$. Un acumulador de fase con incrementos potencia de 2 es, formalmente, un divisor de frecuencia. Si se aplica este mismo principio para registros con mayor cantidad de bits y usando incrementos arbitrarios, conseguimos frecuencias diferentes.
Asumamos que la señal de salida de nuestro "oscilador" será siempre el bit más significativo de un registro de 16 bits y nuestro reloj va a 300 MHz. Eso significará que, incrementando el registro de 1 en 1, el bit más significativo cambiará a razón de:
$$ {300000000 \over {2^N}} = 4577 \: Hz $$
Si en lugar de incrementar el registro de 1 en 1, lo incrementamos de 2 en 2, la cantidad de pulsos que tarde en desbordarse el registro será menor, por tanto, la frecuencia del bit más significativo será mayor, es decir, la frecuencia del bit más significativo es proporcional al valor de incremento del registro. El máximo valor de incremento será $2^{N-1}$ para N bits (es decir un 1 seguido de N-1 ceros) que hará que el registro se comporte de la siguiente manera:
...
Pulso: 0000000000000000 --> 1000000000000000
Pulso: 1000000000000000 --> 0000000000000000
Pulso: 0000000000000000 --> 1000000000000000
Pulso: 1000000000000000 --> 0000000000000000
...
En este caso extremo tenemos que la frecuencia del bit más significativo es de 150 MHz (para una frecuencia de pulso de 300 MHz). De forma genérica tenemos que el valor de incremento para una frecuencia dada puede calcularse de la siguiente forma:
$$ I = {{f_{deseada}} \over 300000000} \times 2^{N} $$
En nuestro caso, si queremos emitir a 87.5 MHz hay que usar un valor de N=54 bits para que el valor de incremento no sea fraccionario:
$$ I_{central} = {87500000 \over 300000000} \times 2^{54} = 5254199565265579 $$
Ese valor es el que habría que usar como valor de incremento en cada pulso de reloj para que en el bit más significativo del registro de 54 bits (bit 53) tengamos una señal a 87.5 MHz. Nótese que para valores de incremento que no sean potencias de 2, obtendremos señales no cuadradas o de fase algo irregular (en el anterior post dedicado a la transmisión FM se profundiza en este tema), pero para el caso que nos ocupa, la "calidad" de la señal resultante no es significativa, lo importante es que la frecuencia fundamental sea la correcta. Para hacer modulación en frecuencia hemos de modificar esta frecuencia en el rango de -75 KHz y +75 KHz, lo que nos genera los siguiente incrementos mínimos y máximos:
$$ I_{min} = {(87500000 - 75000) \over 300000000} \times 2^{54} = 5249695965638208 $$
$$ I_{max} = {(87500000 + 75000) \over 300000000} \times 2^{54} = 5258703164892949 $$
Si calculamos la diferencia entre los incrementos y la dividimos entre dos nos dará el valor 4503599627370.5 que es la amplitud máxima que deberá tener la señal del ADC para que modifique el valor del incremento y que este, a su vez, genere una variación máxima de +- 75 KHz en la frecuencia portadora.
Como la salida del ADC da valores entre -8191 y +8191 a este valor hay que multiplicarle el valor ${4503599627370.5 \over 8191} = 549822930$ para que valores próximos a -8191 en la salida del ADC generen una portadora de 87.5 MHz - 75 KHz = 87.425 MHz y valores próximos a +8191 en la salida del ADC generen una portadora de 87.5 MHz + 75 KHz = 87.575 MHz. El valor del incremento del acumulador de fase que genera la señal de la antena será el siguiente:
$$ I = I_{central} + (ADC \times 549822930) = 5254199565265579 + (ADC \times 549822930) $$
A continuación puede verse el código fuente completo (cabe en un único fichero VHDL).
library ieee; use ieee.std_logic_1164.all; use ieee.numeric_std.all; entity MAX10FMTransmitter is port ( Clk : in std_logic; AnalogComparator : in std_logic; PWM : out std_logic; Antenna : out std_logic; Led : out std_logic_vector(7 downto 0) ); end entity; architecture A of MAX10FMTransmitter is component PLL port ( inclk0 : in std_logic := '0'; c0 : out std_logic ); end component; signal Clk300 : std_logic; signal ADCFollowerD : std_logic; signal ADCFollowerQ : std_logic; signal ADCScalerD : std_logic_vector(12 downto 0); signal ADCScalerQ : std_logic_vector(12 downto 0); signal ADCAccumulatorD : std_logic_vector(13 downto 0); signal ADCAccumulatorQ : std_logic_vector(13 downto 0); -- signed value: -8191 to +8191 signal ADCOutputD : std_logic_vector(13 downto 0); signal ADCOutputQ : std_logic_vector(13 downto 0); signal PhaseAccumulatorD : std_logic_vector(53 downto 0); signal PhaseAccumulatorQ : std_logic_vector(53 downto 0); signal PhaseAccumulatorIncD : std_logic_vector(53 downto 0); signal PhaseAccumulatorIncQ : std_logic_vector(53 downto 0); -- increment for phase accumulator to transmit at 87.5 MHz: (87500000 / 300000000) * (2^54) = 5254199565265579 --constant TxCentralFrequencyInc : integer := 5254199565265579; -- must fit in 54 bits constant TxCentralFrequencyIncL : integer := 2863311531; -- 32 bits constant TxCentralFrequencyIncH : integer := 1223338; -- 22 bits constant TXCentralFrequencyInc : signed(53 downto 0) := to_signed(TxCentralFrequencyIncH, 22) & to_signed(TxCentralFrequencyIncL, 32); -- gain for ADC output constant ADCGain : integer := 549822930; -- ADCGain needs 30 bits begin -- PLL to obtain 300 MHz from external 12 MHz P : PLL port map ( inclk0 => Clk, c0 => Clk300 ); -- ADC process (Clk300) begin if (Clk300'event and (Clk300 = '1')) then ADCFollowerQ <= ADCFollowerD; end if; end process; ADCFollowerD <= AnalogComparator; PWM <= ADCFollowerQ; process (Clk300) begin if (Clk300'event and (Clk300 = '1')) then ADCScalerQ <= ADCScalerD; end if; end process; ADCScalerD <= std_logic_vector(unsigned(ADCScalerQ) + 1); process (Clk300) begin if (Clk300'event and (Clk300 = '1')) then ADCAccumulatorQ <= ADCAccumulatorD; end if; end process; ADCAccumulatorD <= std_logic_vector(to_signed(0, 14)) when (unsigned(ADCScalerQ) = 0) else std_logic_vector(signed(ADCAccumulatorQ) + to_signed(1, 14)) when (ADCFollowerQ = '1') else std_logic_vector(signed(ADCAccumulatorQ) - to_signed(1, 14)) when (ADCFollowerQ = '0') else ADCAccumulatorQ; process (Clk300) begin if (Clk300'event and (Clk300 = '1')) then ADCOutputQ <= ADCOutputD; end if; end process; ADCOutputD <= ADCAccumulatorQ when (unsigned(ADCScalerQ) = 0) else ADCOutputQ; Led <= ADCOutputQ(13 downto 6); -- phase accumulator process (Clk300) begin if (Clk300'event and (Clk300 = '1')) then PhaseAccumulatorQ <= PhaseAccumulatorD; end if; end process; PhaseAccumulatorD <= std_logic_vector(unsigned(PhaseAccumulatorQ) + unsigned(PhaseAccumulatorIncQ)); Antenna <= PhaseAccumulatorQ(53); -- phase accumulator increment control (output frequency control) process (Clk300) begin if (Clk300'event and (Clk300 = '1')) then PhaseAccumulatorIncQ <= PhaseAccumulatorIncD; end if; end process; -- 14 bits * 40 bits = 54 bits PhaseAccumulatorIncD <= std_logic_vector((signed(ADCAccumulatorQ) * to_signed(ADCGain, 40)) + TxCentralFrequencyInc) when (unsigned(ADCScalerQ) = 0) else PhaseAccumulatorIncQ; end architecture;
El bit 53 del registro acumulador de fase se saca por un pin de la FPGA y en dicho pin se puede colocar un simple trozo de cable. No es necesario hacer ningún circuito que acondicione la señal de salida.
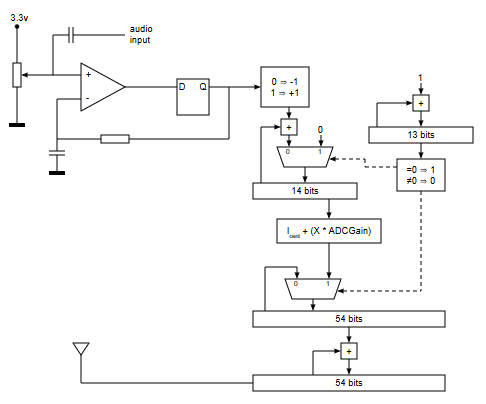
Si a corta distancia del circuito ponemos un receptor de radio FM comercial sintonizado a 87.5 MHz podremos escuchar la señal que está leyendo el ADC de la FPGA y que está siendo transmitida en FM.
Código fuente disponible en la sección soft.
Lo sentimos. No se permiten nuevos comentarios después de 90 días.

 Calendario
Calendario




