Las redes neuronales son un tópico que se ha vuelto a poner de moda gracias al concepto del "deep learning" y a la irrupción de las redes neuronales convolucionales, que han revolucionado, sobre todo, las técnicas de reconocimiento de imágenes. No vamos a llegar tan lejos: implementaremos un sencillo perceptrón multicapa (MLP) en un Arduino que permita a este aprender y predecir el comportamiento de un usuario que acciona unos botones. No es un juego especialmente entretenido pero sirve como prueba de concepto de la implementación de redes neuronales artificiales sobre sistemas embebidos.

Perceptrón multicapa (MLP)

En un post anterior se explicaron los fundamentos teóricos de los perceptrones multicapa. Tenemos un conjunto de neuronas dispuestas en cascada, las de un extremo son las neuronas de entrada y las del otro extremo son las neuronas de salida.



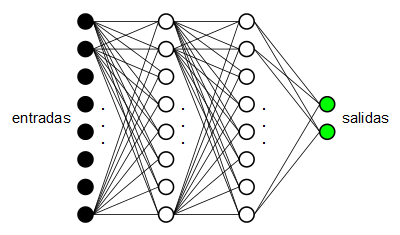
Cada capa de neuronas está conectada con la capa inmediatamente anterior mediante un conjunto de pesos sinápticos que determinan el nivel de influencia de cada neurona de la capa (i-1)-ésima con cada neurona de la capa i-ésima. Los valores de entrada pasan por la matriz de pesos sinápticos que une la capa de entrada con la primera capa intermedia y determinan los valores de las neuronas de la primera capa oculta, a continuación este primera capa oculta propaga sus valores a través de otra matriz de pesos que une dicha capa con la siguiente y así sucesivamente hasta llegar a la capa de salida. La salida del perceptrón multicapa serán las salidas de las neuronas de la última capa.

La salida de cada neurona oculta y de salida viene determinada por:
$$suma^{o}_{pk} = \sum_{j=1}^{L}w_{kj}^{o}y_{pj} + \theta_{k}^{o}$$
$$y_{pk}=f_{k}^{o}(suma^{o}_{pk})$$
Siendo:
$w_{kj}^{o}$ el peso sináptico de la neurona $j$ de la capa anterior sobre la neurona $k$ de la capa actual.
$f$ la función de activación (en este caso la sigmoide).
$$f(x) = {{1} \over {1+e^{-x}}}$$
Cada neurona puede representarse de forma gráfica de la siguiente manera:

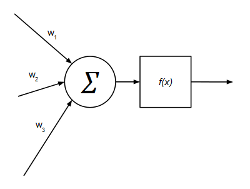
Por ejemplo, un perceptrón multicapa con 6 entradas, 2 salidas y una capa ocultas con 4 neuronas tendrá la siguiente configuración:

A0 = {a01, a02, a03, a04, a05, a06}   <-- capa de entrada
W0,1 = {                              <-- pesos sinápticos entre la entrada y la capa oculta
    w11 w12 w13 w14 w15 w16
    w21 w22 w23 w24 w25 w26
    w31 w32 w33 w34 w35 w36
    w41 w42 w43 w44 w45 w46
}
A1 = {a11 a12 a13 a14}                <-- capa oculta
X1,2 = {                              <-- pesos sinápticos entre la capa oculta y la salida
    x11 x12 x13 x14
    x21 x22 x23 x24
}
A2 = {a21 a22}                        <-- capa de salida

Recomiendo leer el post anterior donde se explica de forma más pormenorizada tanto el perceptrón multicapa como el algoritmo de aprendizaje "backpropagation", el más utilizado y el usado en esta prueba de concepto.

Juego de predicción

Se plantea un sencillo juego de predicción en el que el Arduino deberá aprenderse los movimientos del usuario que interactúa con él. Se disponen 4 pulsadores y 4 leds (a cada led le corresponde un botón y viceversa). Se incluyen además dos pulsadores adicionales etiquetados como "ENTRENAR" y "EVALUAR" y dos leds adicionales etiquetados como "ENTRENAMIENTO TERMINADO" y "EVALUANDO". Se implementa una red neuronal de tipo MLP con 8 entradas, una capa oculta de 8 neuronas y una capa de salida de 4 neuronas. 4 de las neuronas de entrada recogen las entradas de los 4 pulsadores (1 = pulsado, 0 = no pulsado) y las 4 neuronas de entrada restantes reciben el valor de los pulsadores del instante anterior (es una forma de dar memoria a la red), las cuatro neuronas de salida están conectadas a los 4 leds de salida (encendido = salida de la neurona mayor que 0.5, apagado = en caso contrario).

En modo evaluación el Arduino cada vez que detecta la pulsación de un botón aplica los valores correspondientes a las 8 neuronas de entrada, evalúa el MLP y emite el valor de las 4 neuronas de salida a los leds. En modo entrenamiento la red se va entrenando a sí misma observando las pulsaciones del usuario. La mecánica del "juego" es la siguiente:

1. Nada más arrancar el Arduino, inicia en modo EVALUACIÓN e ilumina el led "EVALUANDO". En este modo cada vez que se pulsa uno de los 4 pulsadores de entrada se evalúa la red neuronal y se emite la salida correspondiente. Como inicialmente los pesos sinápticos son aleatorios, los leds actuarán de forma aleatoria en función de la entrada.

2. Cuando queramos entrenar la red neuronal, pulsamos "ENTRENAR". Esto hace que el led "EVALUANDO" se apague para indicar que estamos en modo aprendizaje y la red entra en modo de aprendizaje. El usuario empieza a accionar los pulsadores en el orden que quiera, se asume una secuencia de cuatro pulsaciones de tal manera que cada cuatro pulsaciones, la red es entrenada para que sea capaz de aprenderse la secuencia. Cada vez que terminamos de introducir una secuencia (cuatro pulsaciones), la red es entrenada con la secuencia introducida y se ilumina el led "ENTRENAMIENTO TERMINADO", si seguimos repitiendo la secuencia afianzaremos el aprendizaje de la red neuronal.

3. Una vez que el led "ENTRENAMIENTO TERMINADO" se haya iluminado al menos una vez podemos volver al modo de evaluación accionando el pulsador "EVALUAR". Al entrar de nuevo en el modo de evaluación se iluminará el led "EVALUANDO". Tras el entrenamiento la red tendrá los pesos sinápticos modificados por el aprendizaje de tal manera que intentará predecir qué pulsador accionará el jugador en cada momento.

Veamos un ejemplo:

1. Encendemos y esperamos a que se encienda el led "EVALUANDO". Comprobamos que al accionar cualquiera de los 4 pulsadores los leds de salida se encienden y se apagan sin criterio, de forma aleatoria debido a los pesos sinápticos aleatorios.

2. Pulsamos "ENTRENAR" y esperamos a que se apague el led "EVALUANDO". Ahora estamos en modo aprendizaje (o entrenamiento).

3. Nos inventamos una secuencia, por ejemplo {1, 4, 2, 3} y vamos accionando los pulsadores de entrada en ese orden. Cuando pulsemos el último número de la secuencia, el 3, se aplicará el algoritmo de aprendizaje para entrenar la red neuronal y una vez termine, se encenderá el led "ENTRENAMIENTO TERMINADO".

4. Llegamos a este punto podemos seguir entrenando la red con la misma secuencia (volvemos a introducir la secuencia en orden {1, 4, 2, 3}, al pulsar el 1 se apagará el led "ENTRENAMIENTO TERMINADO" y volverá a encenderse cuando pulsemos el 3 para indicar que se ha realizado otro entrenamiento) o podemos pasar al modo de evaluación.

5. Para pasar al modo de evaluación pulsamos "EVALUAR". Esto hará que el led "EVALUANDO" se encienda y ahora podremos probar la red entrenada.

6. En modo evaluación lo que hace la red es tratar de adivinar qué pulsador se accionará en el siguiente movimiento. Por ejemplo en nuestro caso, para la secuencia {1, 4, 2, 3}, ocurrirá lo siguiente:

pulsamos 1 --> se enciende el 4
pulsamos 4 --> se enciende el 2
pulsamos 2 --> se enciende el 3
pulsamos 3 --> se enciende el 1

Como se puede comprobar, la red neuronal se ha aprendido nuestros movimientos correctamente.

Implementación

A continuación puede verse el diagrama de clases utilizado en la implementación del juego de predicción en C++:


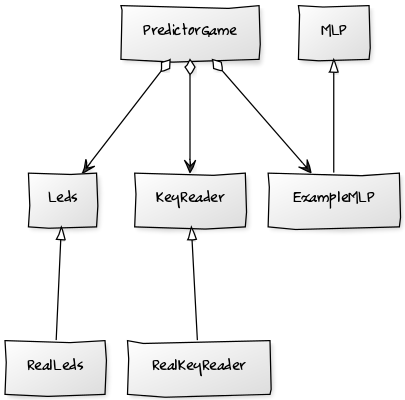
Se trata de una estructura de código muy sencilla. La clase PredictorGame mantiene la máquina de estados principal del juego, lee los pulsadores, controla las luces e incluye también la red neuronal (ExampleMLP). La clase MLP es una clase abstracta que permite definir mediante la implementación de varios de sus métodos virtuales puros la topología de un perceptrón multicapa cualquiera (entradas, capas ocultas y neuronas de salida). La clase ExampleMLP es una especialización de MLP con la topología descrita: 8 entradas, 1 capa intermedia oculta con 8 neuronas y una capa de salida de 4 neuronas.


El código fuente está organizado de tal manera que el que es independiente de la plataforma (clases MultilayerPerceptron, ExampleMultilayerPerceptron, KeyReader, Leds y PredictorGame) se encuentra en la carpeta raiz. El código dependiente de cada plataforma se encuentra en la carpeta correspondiente a dicha plataforma: dentro de la carpeta "linux" están las clases "LinuxKeyReader" y "LinuxLeds" así como el fichero "main.cc" para Linux y dentro de la carpeta "arduino" están las clases "RealKeyReader" y "RealLeds" así como el fichero "main.cc" para Arduino. En este caso concreto, las clases "RealKeyReader" y "RealLeds" están especializadas para el patillaje del Arduino Leonardo pero son fácilmente adaptables a otros modelos de Arduino.

Para compilar la versión "linux" basta con entrar en la carpeta "linux" y hacer "make" mientras que para compilar la versión "arduino" hay que ir a la carpeta "arduino", editar el fichero "Makefile", poner los valores adecuados para la carpeta donde está instalado el IDE de Arduino ("ARDUINO_FOLDER") y el puerto serie donde se conecta el Arduino ("SERIAL") y a continuación hacer "make" para generar el fichero "main.hex" y "make install" para tostarlo en el Arduino.

A nivel eléctrico se trata de un circuito sumamente sencillo: 6 pulsadores, con su pequeña red antirrebote cada uno, y 6 leds.

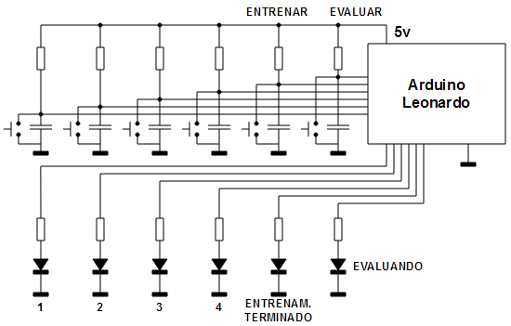
Todo el código está disponible en la sección soft.

---

Lo sentimos. No se permiten nuevos comentarios después de 90 días.

---

- Página generada en 0.034 segundos | Site Views: 172791