Registro de aproximaciones sucesivas (SAR)
Esta técnica utiliza un comparador, una resistencia y un condensador como únicos componentes externos y consume dos pines E/S de la FPGA. Se consigue una resolución en bits arbitraria que sólo dependerá de los valores de R, de C y de la frecuencia de reloj de la FPGA.
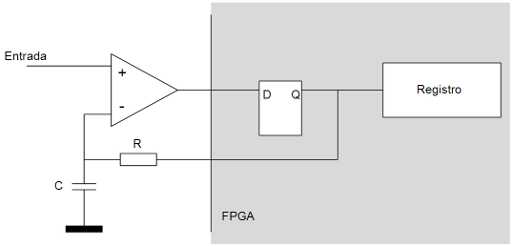
El principio de funcionamiento es muy sencillo: inicialmente el condensador se encuentra descargado y la salida de realimentación (el pin conectado a R) se pone a 1. Esto hace que el condensador empiece a cargarse. En el instante en que el voltaje en el condensador llegue hasta la mitad de Vcc (1.65v en el caso de una FPGA alimentada a 3.3v), la FPGA lee el valor de la entrada digital (el otro pin). Esta entrada está conectada a la salida de un comparador que emitirá 3.3v si el voltaje en la entrada V+ es superior al voltaje en la entrada V- y 0v en caso contrario.
Si la FPGA lee un 0 en esa entrada significará que el voltaje que estamos midiendo en la entrada V+ se encuentra por debajo de Vcc/2 por lo que ya podemos determinar que el bit más significativo del valor convertido es un 0. Si la FGPA lee un 1 en esa entrada significará que el voltaje que estamos midiendo en la entrada V+ se encuentra por encima de Vcc/2 por lo que ya podemos determinar que el bit más significativo del valor convertido es en este caso un 1.
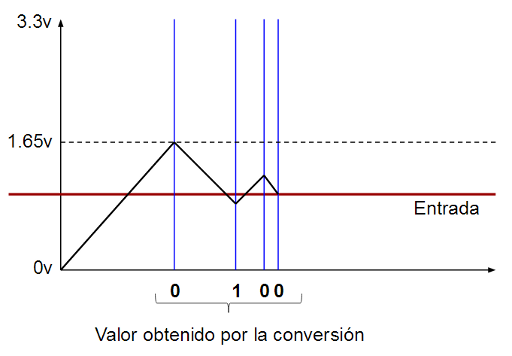
Si la FPGA ha leido un 0 en la entrada de comparación (V+ está por debajo del voltaje que hay en ese instante en los extremos del condensador, Vcc/2), significará que para determinar el siguiente bit hay que bajar el voltaje de la entrada V- (descargar el condensador), por lo que se emite un 0 por el pin conectado a R. Esto provoca que el condensador empiece a descargarse.
Si la FPGA leyó un 1 en la primera comparación (V+ está por encima del voltaje que hay en ese instante en los extremos del condensador, Vcc/2), significará que para determinar el siguiente bit hay que seguir cargando el condensador (la FPGA debe seguir emitiendo un 1 por la pata que conecta a R).
Independientemente de si la FPGA emite un 0 (para descargar el condensador) o un 1 (para seguir cargándolo), espera la mitad de tiempo que la primera vez antes de volver a leer la entrada conectada al comparador. En esta segunda lectura vuelve a hacer lo mismo: Si vale 0 significa que el voltaje del condensador está por encima del voltaje que estamos midiendo (V+) mientras que si vale 1 significa que el voltaje del condensador está por debajo del voltaje que estamos midiendo. En el primer caso el siguiente bit valdrá 0 y se emite un 0 por el pin conectado a R para descargar del condensador. En el segundo caso el siguiente bit valdra 1 y se emitirá un 1 por el pin conectado a R para cargar el condensador. Como puede observar el bit que se emite como valor es el mismo que el que alimenta a la salida conectada a R.
En cada iteración del proceso se espera la mitad de tiempo que la iteración anterior, se empieza siempre por el bit más significativo y se pueden realizar tantas iteraciones como se deseen: La cantidad de bits de resolución de la conversión vendrá determinada por la cantidad de comparaciones que hagamos.
Implementación: el circuito
En este caso se ha implementado una pequeña prueba de concepto: un conversor de 4 bits de resolución usando un amplificador operacional barato LM358N (por AliExpress se pueden adquirir 10 unidades por menos de 2¤ en el momento que escribo estas líneas) para usarlo como comparador, un condensador de 1uF y una resistencia de 10K.
Como FPGA he utilizado una Cyclone II de Altera que pillé hace poco. No es tan potente como la Spartan-3E de Xilinx que he usado en otros montajes pero es compacta, barata y más que suficiente para el ADC.
Implementación: el software
Como se vió en la descripción varios párrafos más arriba, la FPGA debe leer la entrada de comparación en unos instantes determinados: inicialmente debe esperar hasta que el condensador llegue a Vcc/2 para realizar la primera medida, la segunda medida la realizará en la mitad de tiempo que la primera, la tercera en la mitad de tiempo que la segunda y así sucesivamente.
En nuestro caso, asumiendo un condensador de 1uF (C = 0.000001), una resistencia de 10K (R = 10000), la salida de la FPGA que está conectada a R, a la que etiquetaremos como Vi con un valor de 3.3v y la entrada inversora del comparador, a la que llamaremos Vo con un valor de 1.65v (3.3 / 2), tenemos que:
$$t=-R \times C \times log\left({{V_o - V_i} \over {V_o(0) - V_i}}\right)$$
$$t = -10000 \times 0.000001 \times log\left({{1.65 - 3.3} \over {0 - 3.3}}\right) = 0.006931471805599453 \; s$$
Es el tiempo que tarda Vo en valer 1.65v (la mitad de Vcc = 3.3v) partiendo de 0v (condensador totalmente descargado). Esta ecuación es la solución analítica a la ecuación diferencial de la carga de un circuito RC que vimos en este post anterior.
Si asumimos una frecuencia de reloj de 50MHz tenemos que hacen falta:
$$50000000 * 0.006931471805599453 = 346574 \; ciclos$$
Para esperar desde que el condensador está totalmente descargado hasta que Vo = 1.65v. Como se va a hacer una conversión de 4 bits los puntos de comparación se deberán hacer en los siguientes instantes:
1ª comparación (bit 3): 346574 ciclos de reloj
↓
346574 / 2
↓
2ª comparación (bit 2): 173286 ciclos de reloj (instante 519860)
↓
173286 / 2
↓
3ª comparación (bit 1): 86643 ciclos de reloj (instante 606503)
↓
86643 / 2
↓
4ª comparación (bit 0): 43321 ciclos de reloj (instante 649824)Tras hacer la 4ª comparación es necesario realizar una descarga completa del condensador para iniciar la siguiente conversión. Si asumimos el peor de los casos, que el condensador esté totalmente cargado (Vo(0) = 3.3v), tenemos que para llegar a Vo = 0.01v con Vi = 0 se necesitan:
$$-10000 \times 0.000001 \times log\left({{0.01 - 0} \over {3.3 - 0}}\right) = 0.057990926544605255 \; segundos$$
Que equivalen a:
$$50000000 \times 0.057990926544605255 = 2899546 \; ciclos$$
Desde un punto de vista teórico el condensador nunca se descarga del todo (siempre tiene carga residual). Si se pusiese 0 en lugar 0.01 en la ecuación anterior el tiempo tendería a infinito, por lo que hay que poner una cantidad muy baja que no sea cero. De forma global se ve que cada conversión requiere:
649824 ciclos para la conversión en sí + 2899546 ciclos para descargar el condensador del todo antes de iniciar una nueva conversión = 3549370 ciclos
Para contar 3549370 ciclos (desde 0 hasta 3549369) hacen falta como mínimo 22 bits ($2^{21} = 2097152$, se queda corto, y $2^{22} = 4194304$). Por tanto el "motor" de nuestro conversor analógico-digital de 4 bits será un contador de 22 bits que emitirá las siguientes señales de control:
0 --> forzar biestable de comparación = 1
346574 --> cargar el biestable con el 1º valor de comparación
346575 --> empujar valor biestable en registro de desplazamiento (bit 3)
519860 --> cargar el biestable con el 2º valor de comparación
519861 --> empujar valor biestable en registro de desplazamiento (bit 2)
606503 --> cargar el biestable con el 3º valor de comparación
606504 --> empujar valor biestable en registro de desplazamiento (bit 1)
649824 --> cargar el biestable con el 4º valor de comparación
649825 --> empujar valor biestable en registro de desplazamiento (bit 0)
forzar biestable de comparación = 1
649826 --> cargar registro de salida desde registro de desplazamientoEl proceso de descarga se realizará entre el ciclo 649825 y el 4194303 ($2^{22} - 1$). No se va a reiniciar el contador en el ciclo 3549370 para evitar sobrecargar con más puertas lógicas el diseño, sino que se va a dejar que el contador se desborde de forma natural en el ciclo 4194304 ($2^{22}$). Se pierde una centésima de segundo en resolución temporal pero para el caso que nos ocupa no es relevante. Aprovechar el mismo registro contador de tiempo como máquina de estados simplifica enormemente el diseño.
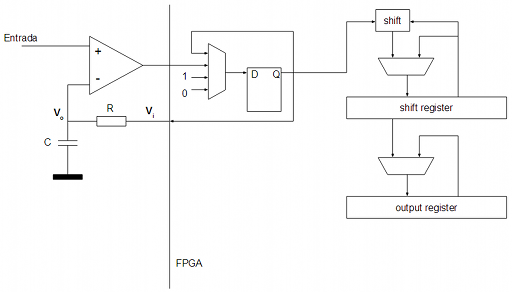
La implementación en VHDL partiendo de este diagrama es muy sencilla:
library ieee; use ieee.std_logic_1164.all; use ieee.numeric_std.all; entity ADC is port ( Clock : in std_logic; Reset : in std_logic; CompIn : in std_logic; ChargeOut : out std_logic; DataOut : out std_logic_vector(3 downto 0) ); end entity; architecture A of ADC is signal DComp : std_logic; signal QComp : std_logic; signal CompSel : std_logic_vector(1 downto 0); signal DCounter : std_logic_vector(21 downto 0); signal QCounter : std_logic_vector(21 downto 0); signal DShiftReg : std_logic_vector(3 downto 0); signal QShiftReg : std_logic_vector(3 downto 0); signal ShiftRegEnable : std_logic; signal DOutReg : std_logic_vector(3 downto 0); signal QOutReg : std_logic_vector(3 downto 0); signal OutRegEnable : std_logic; constant Conversion1Cycle : integer := 346574; constant Conversion2Cycle : integer := 519860; constant Conversion3Cycle : integer := 606503; constant Conversion4Cycle : integer := 649824; begin -- comparator d flip-flop process (Clock) begin if (Clock'event and (Clock = '1')) then QComp <= DComp; end if; end process; DComp <= '0' when ((CompSel = "00") or (Reset = '1')) else '1' when (CompSel = "01") else CompIn when (CompSel = "10") else QComp; ChargeOut <= QComp; -- shift register process (Clock) begin if (Clock'event and (Clock = '1')) then QShiftReg <= DShiftReg; end if; end process; DShiftReg <= (QShiftReg(2 downto 0) & QComp) when (ShiftRegEnable = '1') else QShiftReg; -- output register process (Clock) begin if (Clock'event and (Clock = '1')) then QOutReg <= DOutReg; end if; end process; DOutReg <= QShiftReg when (OutRegEnable = '1') else QOutReg; DataOut <= QOutReg; -- 22 bit counter & fsm process (Clock) begin if (Clock'event and (Clock = '1')) then QCounter <= DCounter; end if; end process; DCounter <= std_logic_vector(to_unsigned(0, 22)) when (Reset = '1') else std_logic_vector(to_unsigned(to_integer(unsigned(QCounter)) + 1, 22)); CompSel <= "00" when (to_integer(unsigned(QCounter)) = (Conversion4Cycle + 1)) else "01" when (to_integer(unsigned(QCounter)) = 0) else "10" when ((to_integer(unsigned(QCounter)) = Conversion1Cycle) or (to_integer(unsigned(QCounter)) = Conversion2Cycle) or (to_integer(unsigned(QCounter)) = Conversion3Cycle) or (to_integer(unsigned(QCounter)) = Conversion4Cycle)) else "11"; ShiftRegEnable <= '1' when ((to_integer(unsigned(QCounter)) = (Conversion1Cycle + 1)) or (to_integer(unsigned(QCounter)) = (Conversion2Cycle + 1)) or (to_integer(unsigned(QCounter)) = (Conversion3Cycle + 1)) or (to_integer(unsigned(QCounter)) = (Conversion4Cycle + 1))) else '0'; OutRegEnable <= '1' when (to_integer(unsigned(QCounter)) = (Conversion4Cycle + 2)) else '0'; end architecture;
Conclusión
Usar un registro de aproximaciones sucesivas (SAR) es la forma más sencilla y barata de implementar un ADC, aunque tiene sus inconvenientes:
- Las conversiones son lentas. Aunque pongamos condensadores y resistencias pequeños, es complicado aumentar la frecuencia de muestreo por encima de unos pocos KHz.
- La pendiente de carga de un condensador en un circuito típico RC no es lineal por lo que la conversión resultante tampoco será lineal. Este escollo puede superarse con un circuito externo más elaborado que garantice una corriente de carga constante en el condensador y, por tanto, una pendiente de carga constante en el mismo.
También tiene sus ventajas :-):
- Usa relativamente pocos recursos de la FPGA.
Muy pocos componentes externos. El comparador podría implementarse incluso utilizando las entradas diferenciales que todas las FPGAs tienen (LVDS, mini-LVDS, etc.).
- La resolución en bits es arbitraria y sólo depende de la implementación interna en la FPGA.
A continuación puede verse un vídeo con el conversor implementado al que se le han conectado cuatro leds:
Todo el código puede descargarse de la sección soft.
Lo sentimos. No se permiten nuevos comentarios después de 90 días.

 Calendario
Calendario




