Punto de partida
En este post anterior se diseñó e implementó un reproductor de sonido para el Teensy que almacenaba un bucle en la memoria flash del microcontrolador. Se utilizó el DAC de 12 bits que viene de serie con el microcontrolador MK20 del Teensy y para el envío de muestras a dicho DAC se usó la interrupción periódica Systick, que traen de serie todos los microcontroladores ARM Cortex-M, ajustada a la frecuencia de muestreo.
void systick() __attribute__ ((section(".systick"))); void systick() { DACDAT = next sample } int main() { // configure DAC SIM_SCGC2 |= (1 << 12); // enable DAC clock generator DAC0_C1 = 0x00; // disable DAC DMA DAC0_C0 = 0xC0; // enable DAC for VREF2 (3.3v) // configure SYSTICK SYST_RVR = F_CPU / SAMPLE_RATE; SYST_CVR = 0; SYST_CSR |= 0x07; while (1) ; }
Objetivo
El objetivo planteado en este caso era implementar un pequeño sintetizador monofónico partiendo de ese mismo modelo (interrupción Systick + DAC). Los bloques planteados para el mini sintetizador son los siguientes:
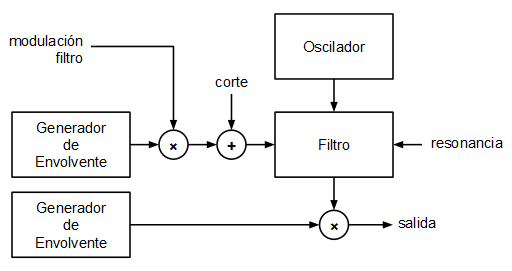
El oscilador
Se ha planteado un oscilador muy sencillo basado en tabla de ondas. Un oscilador basado en tabla de ondas consiste en uno o varios arrays con los valores de la onda que queremos generar, en cada array se guarda un único ciclo de onda y el oscilador lo que hace para emitir tonos a diferente frecuencia es recorrer dicha tabla a diferentes velocidades dando la vuelta cuando llega al final:
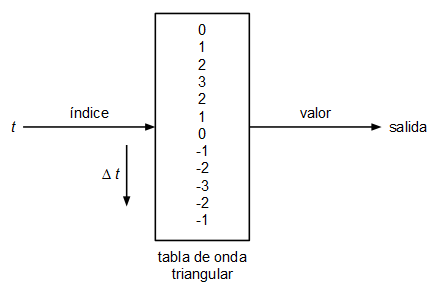
El tamaño de la tabla de ondas vendrá determinado por la resolución (calidad) que queramos darle y por la frecuencia de muestreo. Imaginemos que tenemos un array con 100 valores de una onda con forma de diente de sierra:
// 100 enteros con signo entre -50 y 49
[-50, -49, -48, -47, ... , 47, 48, 49]
Si la frecuencia de muestreo es de 44100 Hz (la frecuencia de muestreo estándar de calidad CD) y queremos reproducir un tono de 440 Hz (nota LA de la cuarta octava del piano) a partir de esta tabla de ondas el oscilador tendrá que usar un incremento de:
$$\Delta t = {440 \over {44100 \over 100}} = 0.9977324263$$
Esto es, el oscilador tomará la primera muestra de la posición 0 de la tabla, la siguiente muestra la tomará de la posición 0.9977324263, la siguiente de la posición 1.9954648526, y así sucesivamente. Como obviamente se trata de una tabla con posiciones enteras, en cada iteración se coge la muestra más próxima o se interpola.
En este caso se ha optado por usar la muestra en la posición de la parte entera del índice. No es la mejor forma de hacerlo pero sí la más rápida:
| t | índice (parte entera de t) |
|---|---|
| 0 | 0 |
| 0.9977324263 | 0 |
| 1.9954648526 | 1 |
| 2.9931972789 | 2 |
| 3.9909297052 | 3 |
| ... | |
| 99.77324263 | 99 |
| 100.7709750563 | |
| como la tabla mide 100, en este momento se vuelve a empezar, manteniendo la parte fraccionaria | |
| 0.7709750563 | 0 |
| 1.7687074826 | 1 |
| 2.7664399089 | 2 |
| ... | |
Debido a que estamos haciendo la implementación en un procesador sin unidad de coma flotante, se realizan todos los cálculos usando aritmética de punto fijo. El formato elegido es el Q16.16 (16 bits enteros + 16 bits fraccionarios = 32 bits que pueden alojarse en un tipo int32_t). Se definen, además, varias macros para facilitar la comprensión del código:
typedef int32_t fixedpoint_t; #define __FP_INTEGER_BITS 16 #define __FP_FRACTIONAL_BITS 16 #define __TO_FP(a) (((int32_t) (a)) << __FP_FRACTIONAL_BITS) #define __FP_1 (((int32_t) 1) << __FP_FRACTIONAL_BITS) #define __FP_ADD(a, b) (((int32_t) (a)) + ((int32_t) (b))) #define __FP_SUB(a, b) (((int32_t) (a)) - ((int32_t) (b))) #define __FP_MUL(a, b) ((int32_t) ((((int64_t) (a)) * ((int64_t) (b))) >> __FP_FRACTIONAL_BITS)) #define __FP_DIV(a, b) ((int32_t) ((((int64_t) (a)) << __FP_FRACTIONAL_BITS) / ((int64_t) (b))))
El código del método getNextSample del oscilador (el que se invoca para calcular cada muestra) queda, por tanto, como sigue:
fixedpoint_t Oscillator::getNextSample() { if (this->status == STATUS_STOPPED) return 0; else if (this->status == STATUS_STARTED) { fixedpoint_t v = ((fixedpoint_t) Wavetable::VALUES[this->t >> __FP_FRACTIONAL_BITS]); if (this->patch->waveform == OscillatorPatch::WAVEFORM_SQUARE) v = (v > 0) ? __TO_FP(1) : __TO_FP(-1); this->t = __FP_ADD(this->t, this->inc); if (this->t >= Wavetable::SIZE_FP) this->t = __FP_SUB(this->t, Wavetable::SIZE_FP); return v; } else return 0; }
Como se puede ver, el atributo t del objeto es el que se va incrementando y a la hora de determinar qué valor devuelve el método getNextSample() se usa como índice de la tabla simplemente la parte entera de t. Esta decisión no es gratuita e implica que hay que tratar de que los incrementos siempre sean mayores o iguales a 1 para que no se produzcan "escalones" en la señal de salida debido a que se repitan muestras de la tabla: en el ejemplo anterior la primera muestra (t = 0) y la segunda (t = 0.9977324263) serán la misma ya que la parte entera de ambos valores es 0. Para evitar que se produzcan estos escalones se ha optado por incrementar el tamaño de la tabla de ondas.
Si partimos de la base de que la frecuencia del tono es directamente proporcional al incremento de t, se puede buscar un tamaño de tabla tal que, para la frecuencia más baja que se quiera reproducir, se obtenga un incremento de t igual a 1. En efecto, si consideramos que no vamos a reproducir tonos por debajo de los 20 Hz (límite inferior del umbral de audición humano), definiendo las tablas de ondas con un tamaño de
$${44100 \over 20} = 2205 \thinspace muestras$$
Para cualquier tono que queramos reproducir, tendremos siempre un incremento de t mayor o igual a 1. Por otro lado podemos simplificar la ecuación del cálculo del incremento de t:
$$\Delta t = {f_{tono} \over 20}$$
Debido a que el propio cálculo del incremento de t implica una división y las divisiones consumen gran cantidad de recursos en procesadores sin unidad de división (como es el caso del ARM Cortex-M) se ha optado por meter en una tabla los diferentes valores del incremento de t. El índice de dicha tabla es el índice de la nota MIDI (entre 0 y 127).
const fixedpoint_t Wavetable::MIDI_FREQ_INC[128] = { 0, 28384, 30071, 31859, 33754, 35761, 37887, 40140, 42527, 45056 ... 34563955, 36619234, 38796727, 41103701 };
Con esta tabla precalculada sintonizar el oscilador solo requiere una indexación y una asignación:
void Oscillator::noteOn(uint8_t midiKey, uint8_t midiVelocity) { this->inc = Wavetable::MIDI_FREQ_INC[midiKey]; this->status = STATUS_STARTED; }
Generador de envolvente
Se utilizan dos generadores de envolvente independientes. Uno que modula la frecuencia de corte del filtro y otro que modula la amplitud del sonido final, antes de escribirlo en el DAC. El tipo de envolvente más común y el que se ha utilizado en este caso es el tipo ADSR (Attack-Decay-Sustain-Release). Cada envolvente de este tipo posee tres valores característicos: el tiempo de ataque (A), el tiempo de caída (D), el nivel de sostenido (S) y el tiempo de liberación (R). Se puede ver un generador de envolvente como una generador de una señal muy lenta que varía entre 0 y 1.
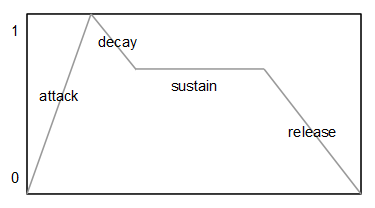
Si se define un nivel de sostenido igual a 0, tenemos una envolvente de tipo AD (Attack-Decay).
Aunque lo más común es definir los parámetro A, D y R en unidades de tiempo (milisegundos, microsegundos), en este caso se ha optado por indicar dichos valores en forma de incrementos, de esta forma no es necesario realizar ninguna multiplicación ni división por cada muestra que se calcula.
fixedpoint_t EnvelopeGenerator::getNextSample() { uint8_t localStatus = this->status; fixedpoint_t ret = 0; do { this->status = localStatus; if (localStatus == STATUS_STOP) ret = 0; else if (localStatus == STATUS_ATTACK) { ret = this->lastSample + this->patch->attackInc; if (ret >= __TO_FP(1)) { ret = __TO_FP(1); localStatus = STATUS_DECAY; } } else if (localStatus == STATUS_DECAY) { ret = this->lastSample - this->patch->decayInc; if (ret <= this->patch->sustainLevel) { ret = this->patch->sustainLevel; if (ret == 0) localStatus = STATUS_STOP; else localStatus = STATUS_SUSTAIN; } } else if (localStatus == STATUS_SUSTAIN) { ret = this->patch->sustainLevel; if (this->noteOffReceived) { this->noteOffReceived = false; localStatus = STATUS_RELEASE; } } else if (localStatus == STATUS_RELEASE) { ret = this->lastSample - this->patch->releaseInc; if (ret <= 0) { ret = 0; localStatus = STATUS_STOP; } } } while (localStatus != this->status); this->lastSample = ret; return __FP_MUL(ret, this->amplitude); }
En la fase de ataque (A) se va incrementando la señal de salida desde 0 hasta 1 en pasos attackInc, en la fase de caída (D) se va decrementando la señal de salida desde 1 hasta el nivel de sostenido en pasos decayInc. Si el nivel de sostenido es 0 la envolvente para al terminar la fase de caída (D), en caso contrario mantiene el nivel de sostenido hasta que se invoca el método noteOff. En ese momento se inicia la fase de liberación (R) decrementando la señal de salida desde el nivel de sostenido hasta 0 en pasos releaseInc.
Filtro
A la hora de implementar un filtro digital existen diferentes aproximaciones: discretización de filtros analógicos conocidos, diseño digital directo usando diagrama de polos y ceros, etc. En este caso se ha optado por una conocida implementación publicada en el libro “Musical Applications of Microprocessors” de Hal Chamberlin. Se trata de una implementación en digital de un filtro de estado variable que permite extraer señales paso bajo, paso banda, paso alto y elimina banda utilizando muy pocos cálculos.
Dicho filtro viene caracterizado por el siguiente sistema de ecuaciones en diferencias:
$$pasoAlto[n] = entrada - ({r \times pasoBanda[n-1]}) - pasoBajo[n]$$
$$pasoBanda[n] = ({f \times pasoAlto[n]}) + pasoBanda[n - 1]$$
$$pasoBajo[n] = ({f \times pasoBanda[n - 1]}) + pasoBajo[n - 1]$$
Siendo:
$$f = 2\sin\left({\pi F_c \over F_s}\right)$$
$$r = {1 \over Q}$$
Siendo $F_c$ la frecuencia de corte del filtro, $F_s$ la frecuencia de muestreo y $Q$ la Q del filtro (la resonancia).
Si se reordenan las ecuaciones en diferencias:
$$pasoBajo[n] = ({f \times pasoBanda[n - 1]}) + pasoBajo[n - 1]$$
$$pasoAlto[n] = entrada - ({r \times pasoBanda[n - 1]}) - pasoBajo[n]$$
$$pasoBanda[n] = ({f \times pasoAlto[n]}) + pasoBanda[n - 1]$$
Podemos olvidarnos de los índices:
pasoBajo += f * pasoBanda
pasoAlto = entrada - (r * pasoBanda) - pasoBajo
pasoBanda += f * pasoAlto
Como se puede apreciar es preciso mantener en memoria al menos las variables “pasoBajo” y “pasoBanda” entre que se procesa una muestra y la siguiente (se trata de un filtro digital de segundo orden).
fixedpoint_t StateVariableFilter::getNextSample(fixedpoint_t input) { this->lowPass = __FP_ADD(this->lowPass, __FP_MUL(this->cutoff, this->bandPass)); fixedpoint_t highPass = __FP_SUB(__FP_SUB(input, this->lowPass), __FP_MUL(this->resonance, this->bandPass)); this->bandPass = __FP_ADD(this->bandPass, __FP_MUL(this->cutoff, highPass)); if (this->mode == MODE_LOWPASS) return this->lowPass; else if (this->mode == MODE_BANDPASS) return this->bandPass; else if (this->mode == MODE_HIGHPASS) return highPass; else if (this->mode == MODE_NOTCH) return __FP_ADD(highPass, this->lowPass); return 0; }
Voz
En la clase Voice juntamos los elementos que se han definido hasta ahora. Esta clase implementa también la interface Generator:
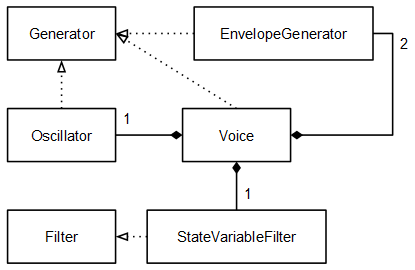
void Voice::noteOn(uint8_t midiKey, uint8_t midiVelocity) { this->oscillator.noteOn(midiKey, midiVelocity); this->ampEnv.noteOn(midiKey, midiVelocity); this->filterEnv.noteOn(midiKey, midiVelocity); } void Voice::noteOff(uint8_t midiKey) { this->oscillator.noteOff(midiKey); this->ampEnv.noteOff(midiKey); this->filterEnv.noteOff(midiKey); } fixedpoint_t Voice::getNextSample() { fixedpoint_t o = this->oscillator.getNextSample(); fixedpoint_t env = __FP_MUL(this->filterEnv.getNextSample(), this->filterEnvMod); fixedpoint_t cutoff = __FP_ADD(env, this->cutoff); if (cutoff < 0) cutoff = 0; else if (cutoff > __TO_FP(1)) cutoff = __TO_FP(1); this->filter.cutoff = cutoff; fixedpoint_t aux = this->filter.getNextSample(o); fixedpoint_t e = this->ampEnv.getNextSample(); return __FP_MUL(aux, e); }
Ahora cada objeto Voice es un sintetizador monofónico. Si en un futuro se quisiese implementar un sintetizador polifónico simplemente habría que instanciar tantos objetos Voice como voces de polifonía se quisieran.
Secuenciador
Aunque en el diagrama inicial no aparece, es fundamental implementar un secuenciador si se quiere probar el sintetizador y no podemos o no queremos pelearnos aún con la implementación de una entrada MIDI. El secuenciador se encarga de disparar notas en determinados instantes de tiempo, en otras palabras, es el objeto que “toca” el instrumento.
En este caso se ha optado por la implementación de un sencillo secuenciador de 16 pasos equidistantes en semicorcheas. 16 semicorcheas forman un compás de 4 por 4 por lo que toca un único compás. El secuenciador vuelve al empezar cuando llega al final: después de tocar la nota de la semicorchea 15, empieza de nuevo en la semicorchea 0.
void Sequencer::setBPM(uint16_t bpm) { uint32_t stepsPerMinute = bpm * 4; // semicorcheas (pasos de secuenciador) por minuto this->n = (Generator::SAMPLES_MS * ((uint32_t) 60000)) / stepsPerMinute; // muestras por semicorchea }
Como el método run se invoca cada vez que se va a generar una muestra (SAMPLE_RATE veces por segundo) se disparará una nota cada vez que un contador interno llegue a n.
void Sequencer::run() { if (this->status == STATUS_PLAY) { if (this->t == 0) { uint8_t note = this->midiNote[this->nextNoteIndex]; if ((note > 0) && (this->generator != NULL)) this->generator->noteOn(note, 100); this->nextNoteIndex++; if (this->nextNoteIndex == SEQUENCE_SIZE) this->nextNoteIndex = 0; } this->t++; if (this->t == this->n) this->t = 0; } }
Nótese que el secuenciador no envía eventos de tipo “noteOff”. Esto está hecho así adrede para este caso concreto por simplicidad, y porque las envolventes que se usan tienen siempre el nivel de sostenido a 0 (el sonido se acaba extinguiendo aunque el secuenciador no envíe eventos “noteOff”). Como la clase Voice implementa la interface Generator, le podemos decir al secuenciador que mande los disparos de nota (“noteOn”) al objeto de tipo Voice:
Voice v;
Sequencer seq;
...
seq.setBPM(120);
seq.setGenerator(v);
De esta forma ya tenemos adecuadamente inicializado el secuenciador. Ahora sólo falta meter las notas MIDI que queramos que toque. Un valor de nota igual a 0 indica al secuenciador que no queremos disparar ninguna nota en esa semicorchea:
seq.midiNote[0] = 36; // Do 1 seq.midiNote[1] = 24; // Do 0 seq.midiNote[2] = 0; seq.midiNote[3] = 36; // Do 1 seq.midiNote[4] = 39; // Re# 1 seq.midiNote[5] = 0; seq.midiNote[6] = 0; seq.midiNote[7] = 39; // Re# 1 seq.midiNote[8] = 36; // Do 1 seq.midiNote[9] = 24; // Do 0 seq.midiNote[10] = 0; seq.midiNote[11] = 36; // Do 1 seq.midiNote[12] = 39; // Re# 1 seq.midiNote[13] = 0; seq.midiNote[14] = 0; seq.midiNote[15] = 43; // Sol 1 seq.start(); // cambiamos el estado interno del secuenciador a STATUS_PLAY
En este caso se ha metido una sencilla secuencia típica de música electrónica, en la escala de Do menor.
Juntándolo todo
El secuenciador invoca al método “noteOn” del objeto Voice cada vez que hay una nota nueva que tocar y el valor devuelto por el método “getNextSample” del objeto de tipo Voice es el que se manda al DAC. La señal debe ser adaptada de fixedpoint_t a entero sin signo de 12 bits (0 - 4095):
void systick() { seq.run(); fixedpoint_t aux = v.getNextSample() >> 1; // evitar clipping uint16_t out; if (aux >= __TO_FP(1)) out = 4095; else if (aux <= __TO_FP(-1)) out = 0; else out = (uint16_t) (((aux + 32768) >> 4) & 0x00000FFF); DACDAT = out; }
Resultados
En la implementación final realizada se ha optado por utilizar una frecuencia de muestreo de 32 KHz. Usar esta frecuencia de muestreo permite generar tonos más precisos ya que 96 MHz no es divisible entre 44.1 KHz pero sí lo es entre 32 KHz (la frecuencia de muestreo es más precisa a 32 KHz que a 44.1 KHz).
A continuación un vídeo en el que puede verse y oirse el invento. No se oye muy alto porque tuve que poner el volumen bajo (era tarde cuando grabé) y encima pasó un camión en ese momento por la calle ¬¬
Todo el código fuente está disponible en la sección soft.
Lo sentimos. No se permiten nuevos comentarios después de 90 días.

 Calendario
Calendario




