Mecánica del juego
Se trata de shooter 3D simplificado: hay que buscar todos los items blancos y dispararles con A para que desaparezcan. En el momento que hemos terminado con todos los items de un nivel, nos vamos al siguiente nivel, y así sucesivamente. En el juego no puedes "morir" simplemente vas cambiado de niveles y cuando terminas el último vuelves a empezar.
Diseño de la pantalla
La única pantalla que tiene el juego está gestionada por la clase TanksMainScreen (en la carpeta games/tanksfp). El dibujado de la escena 3D se realiza en el centro de la pantalla (64x64 pixels). Las zonas de los lados se utilizan para indicar cuantos items o enemigos quedan por abatir en el nivel actual y el número del nivel.
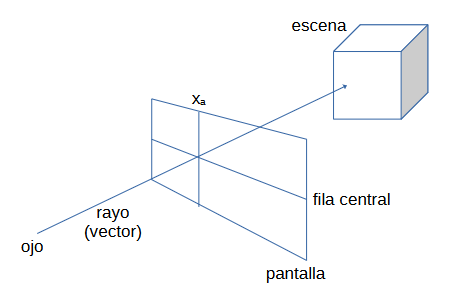
Renderizado de la escena usando raycasting
La técnica del raycasting, la utilizada en muchos de los juegos 3D de los años 90 y principios de los 2000 para dibujar escenas en 3D, se basaba realmente en el cálculo de colisiones de vectores bidimensionales. Para cada columna de la pantalla se calcula un vector 2D (rayo) que va desde el jugador hasta la escena pasando por ese punto de la pantalla.
Si el vector choca con algún muro u objeto, se calcula la distancia a la que choca dicho vector y, por semejanza de triángulos con respecto a la altura del muro u objeto contra el que ha chocado el rayo, se calcula la altura que debe tener esa sección del objeto en la coordenada x por la que ha pasado el rayo.
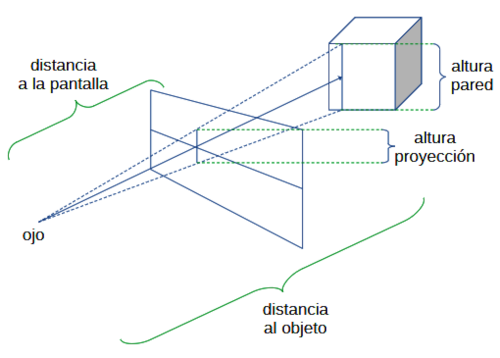
En este caso:
$$\frac{altura\ proyección}{distancia\ a\ la\ pantalla} = \frac{altura\ objeto}{distancia\ al\ objeto}$$
Se define un mundo en dos dimensiones en el que los muros y los items son segmentos y el jugador se mueve en el plano 2D:
const Level TanksMainScreen::LEVELS[] = { { // nivel 0 /* +---+ cada | | es un cuadrado de 10x10 unidades del mundo, P es el jugador +---+ +---+---+---+---+---+---+---+---+ | | + P--> + + | | | + +---+---+---+ | | +---+---+---+---+ + | | | + + + | | | + + + | | +---+---+---+---+---+---+---+---+ */ 80, // width = 80 (integer) 60, // height = 60 (integer) 8, // 8 segments { {{0, 0}, {5242880, 0}}, // scene segments (Q16.16 fixed point) {{5242880, 0}, {5242880, 3932160}}, {{5242880, 3932160}, {0, 3932160}}, {{0, 3932160}, {0, 0}}, {{0, 1966080}, {2621440, 1966080}}, {{2621440, 1966080}, {2621440, 3276800}}, {{3276800, 655360}, {3276800, 1310720}}, {{3276800, 1310720}, {5242880, 1310720}} }, {655360, 655360}, // (10, 10) (Q16.16 fixed point) 0, // player at (10, 10) looking with ANGLE[0] 2 // 2 collectable/shootable items }, // ... other levels };
El algoritmo de pintado "lanza" los 64 rayos correspondientes las 64 columnas de la ventana de la escena 3D (el recuadro de 64x64 pixels que se dibuja en el centro del display LCD) y para cada rayo, se calcula la intersección del mismo con cada uno de los segmentos del mundo y los enemigos (del nivel).
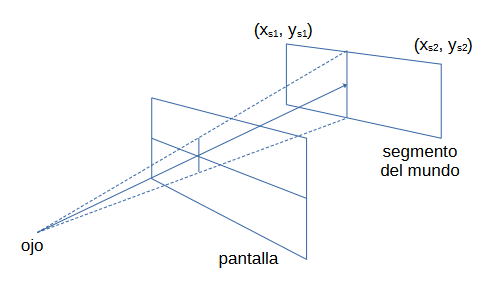
Cada segmento del mundo tendrá dos coordenadas 2D asociadas, mientras que cada rayo estará compuesto por la coordenada del jugador más un vector director unitario apuntando a la columna del display correspondiente. En cada frame, las coordenadas del jugador no cambian, lo que cambia es el vector director (el rayo).
El algoritmo grosso modo sería el siguiente:
para cada coordenada x entre -31 y +31 (se asume que 0 es el centro de la pantalla)
rayo = vector unitario que va desde el jugador y apunta a la columna x
distanciaColision = infinita
segmentoAPintar = ninguno
para cada segmento s del nivel
calcular las posible colisión entre el rayo y s
si colisiona y (distancia < distanciaColision) entonces
distanciaColision = distancia
segmentoAPintar = s
fin si
fin para
si (segmentoAPintar != ninguno) entonces
alturaEnPantalla = ALTURA * distanciaAPantalla / distanciaColision
pintar en la columna x un segmento vertical de tamaño alturaEnPantalla
en caso contrario
pintar en la columna x un punto en el centro (horizonte)
fin si
fin para
Cálculo de las colisiones
Cada segmento $s$ del mundo tendrá dos coordenadas 2D asociadas:
$$
\left( \left( x_{s1}, y_{s1} \right), \left( x_{s2}, y_{s2} \right) \right)
$$
Mientras que cada uno de los 64 rayos que se "lanzan" será un vector de la forma
$\left( \left( x_r , y_r \right), \left( x_{rd} , y_{rd} \right) \right)$ siendo $\left( x_r , y_r \right)$ las coordenadas del jugador en el mapa y $\left( x_{rd} , y_{rd} \right)$ el vector director unitario que apunta hacia el pixel.
Si definimos los puntos del segmento usando ecuaciones paramétricas, tenemos que:
$$
x = x_{s1} + t \left( x_{s2} - x_{s1} \right)\\
y = y_{s1} + t \left( y_{s2} - y_{s1} \right)
$$
Siendo $0 \leq t \leq 1$, de tal manera que:
$$
t = 0 \Rightarrow \left( x, y \right) = \left( x_{s1}, y_{s1} \right)\\
t = 1 \Rightarrow \left( x, y \right) = \left( x_{s2}, y_{s2} \right)
$$
Mientras que si definimos los puntos a lo largo del rayo que trazamos desde el jugador hasta la columna de la pantalla tenemos que:
$$
x = x_{r} + u x_{rd}\\
y = y_{r} + u y_{rd}
$$
Siendo $0 \le u$ y $u$ la distancia desde el jugador hasta $\left( x, y \right)$. A continuación definimos $d_{xs} = x_{s2} - x_{s1}$ y $d_{ys} = y_{s2} - y_{s1}$ y despejamos:
$$
x = x_{s1} + t d_{xs} = x_{r} + u x_{rd}\\
y = y_{s1} + t d_{ys} = y_{r} + u y_{rd}\\
t = \frac{x_{r} + u x_{rd} - x_{s1}}{d_{xs}}\\
u = \frac{y_{s1} + t d_{ys} - y_{r}}{y_{rd}}
$$
Por tanto:
$$
u = \frac{y_{s1} + \frac{x_{r} + u x_{rd} - x_{s1}}{d_{xs}} d_{fs} - y_{r}}{y_{rd}}\\
u y_{rd} = y_{s1} + \frac{x_{r} d_{ys}}{d_{xs}} + u \frac{x_{rd} d_{ys}}{d_{xs}} - \frac{x_{s1} d_{ys}}{d_{xs}} - y_{r}\\
u y_{rd} - u \frac{x_{rd} d_{ys}}{d_{xs}} = y_{s1} + \frac{x_{r} d_{ys}}{d_{xs}} - \frac{x_{s1} d_{ys}}{d_{xs}} - y_{r}\\
u \left( y_{rd} - \frac{x_{rd} d_{ys}}{d_{xs}} \right) = y_{s1} + \frac{x_{r} d_{ys}}{d_{xs}} - \frac{x_{s1} d_{ys}}{d_{xs}} - y_{r}\\
u = \frac{y_{s1} + \frac{x_{r} d_{ys}}{d_{xs}} - \frac{x_{s1} d_{ys}}{d_{xs}} - y_{r}}{y_{rd} - \frac{x_{rd} d_{ys}}{d_{xs}}}
$$
Multiplicando numerador y denominador por $d_{xs}$:
$$
u = \frac{d_{xs} y_{s1} + x_{r} d_{ys} - x_{s1} d_{ys} - y_{r} d_{xs}}{y_{rd} d_{xs} - x_{rd} d_{ys}}
$$
De esta forma ya tenemos calculado $u$ que será la distancia entre el jugador y la recta que contiene el segmento $s$. si $u < 0$ significará que el segmento está detrás del jugador.
Ahora con $u$ calculado, podemos sustituir su valor en:
$$
t = \frac{x_{r} + u x_{rd} - x_{s1}}{d_{xs}}
$$
Lo que nos dará el valor de $t$. Si $t < 0$ o $t > 1$ significará que el rayo no corta con el segmento. Nótese que si $y_{rd} d_{xs} - x_{rd} d_{ys} = 0$ significará que el rayo y la recta que contiene el segmento no se cortan (son paralelos) y debe ser tenido en cuenta para evitar una división entre 0:
TanksMainScreen::Intersection TanksMainScreen::getIntersection(const Segment &seg, const Vector &ray, const fixedpoint_t minRayT, fixedpoint_t &segT, fixedpoint_t &rayT) { fixedpoint_t dxs = seg.p2.x - seg.p1.x; fixedpoint_t dys = seg.p2.y - seg.p1.y; if ((dxs != 0) || (dys != 0)) { fixedpoint_t denRayT = (ray.dir.y * dxs) - (ray.dir.x * dys); if (denRayT != 0) { rayT = ((dxs * seg.p1.y) + (ray.p.x * dys) - (seg.p1.x * dys) - (ray.p.y * dxs)) / denRayT; if (rayT >= minRayT) { if (dxs != 0) segT = (ray.p.x + (rayT * ray.dir.x) - seg.p1.x) / dxs; else segT = (ray.p.y + (rayT * ray.dir.y) - seg.p1.y) / dys; if ((segT >= 0) && (segT <= fixedpoint_t::get(1))) return Intersection::ONE_POINT; } } } return Intersection::NO_POINT; }
Optimizaciones y datos precalculados
Todos los cálculos de precisión decimal se realizan utilizando aritmética de punto fijo en formato Q16.16 (enteros de 32 bits con 16 bits para la parte entera y 16 bits para la parte fraccionaria) y ayudándonos de la sobrecarga de operadores para facilitar la escritura de código y la mantenibilidad del mismo.
class fixedpoint_t { public: int32_t v; fixedpoint_t(int32_t x = 0) : v(x) { }; inline fixedpoint_t &operator = (const int32_t &x) { this->v = x << 16; return *this; }; inline fixedpoint_t operator + (const fixedpoint_t &x) const { fixedpoint_t ret; ret.v = this->v + x.v; return ret; }; inline fixedpoint_t operator - (const fixedpoint_t &x) const { fixedpoint_t ret; ret.v = this->v - x.v; return ret; }; inline fixedpoint_t operator - () const { fixedpoint_t ret; ret.v = -(this->v); return ret; }; inline fixedpoint_t operator * (const fixedpoint_t &x) const { fixedpoint_t ret; ret.v = (((int64_t) this->v) * ((int64_t) x.v)) >> 16; return ret; }; inline fixedpoint_t operator / (const fixedpoint_t &x) const { fixedpoint_t ret; ret.v = (((int64_t) this->v) << 16) / ((int64_t) x.v); return ret; }; inline bool operator == (const fixedpoint_t &x) const { return (this->v == x.v); }; inline bool operator != (const fixedpoint_t &x) const { return (this->v != x.v); }; inline bool operator < (const fixedpoint_t &x) const { return (this->v < x.v); }; inline bool operator > (const fixedpoint_t &x) const { return (this->v > x.v); }; inline bool operator <= (const fixedpoint_t &x) const { return (this->v <= x.v); }; inline bool operator >= (const fixedpoint_t &x) const { return (this->v >= x.v); }; inline fixedpoint_t operator += (const fixedpoint_t &x) { this->v += x.v; return *this; }; inline fixedpoint_t operator -= (const fixedpoint_t &x) { this->v -= x.v; return *this; }; inline int32_t getIntegerPart() { return this->v >> 16; }; inline static fixedpoint_t get(int32_t x) { fixedpoint_t ret; ret.v = x << 16; return ret; }; };
Además existen dos puntos clave en el código donde son necesarios cálculos trigonométricos:
1. El jugador está definido por sus coordenadas y por un vector unitario que apunta a "donde está mirando". Dicho vector coincide con el vector del rayo para la columna 0 de la pantalla por lo que cada rayo será una rotación del vector "hacia donde estoy mirando" y las rotaciones se deben calcular mediante senos y cosenos, así que lo que se hace en este caso es generar unas tablas precalculadas con los senos y los cosenos de los diferentes ángulos necesarios para calcular los 64 rayos de la pantalla. De hecho no hacen falta 64 senos y cosenos, basta con 32, puesto que la pantalla es simétrica.
2. Para que el jugador gire, se hace una rotación de su vector director alrededor de la coordenada del propio jugador y dicha rotación se realiza también aprovechando tablas precalculadas de senos y cosenos sólo para un cuadrante (son simétricos cambiándoles el signo para los otros tres cuadrantes de la circunferencia goniométrica).
Para ayudarnos en la generación de datos precalculados se hacen dos scripts:
- calculate_dir_vector.sh NUM_ÁNGULOS: Genera una tabla precalculada con los senos y los cosenos de NUM_ÁNGULOS en el intervalo $\left[ 0 , \frac{\pi}{2} \right)$. Los valores generador en formato de punto fijo Q16.16 (directamente "copiables y pegables" en el código C++).
- calculate_display_angles.sh DIST_TO_CENTER DISPLAY_WIDTH: Genera una tabla precalculada de 32 registros. Cada registro contiene un ángulo en radianes (no se usa en el código), el seno de ese ángulo, el coseno de ese ángulo y la distancia desde el jugador hasta el punto de la pantalla (el valor "distanciaAPantalla" necesario para calcular correctamente la altura de los objetos proyectados). DIST_TO_CENTER es la distancia desde el jugador hasta el centro de la pantalla en unidades del mundo y DISPLAY_WIDTH es la anchura de la pantalla en unidades del mundo.
A continuación se puede ver cómo queda el código que calcula el trazado de rayos de la pantalla a partir del vector del jugador:
const AngleAndDistance TanksMainScreen::DISPLAY_ANGLES_AND_DISTANCES[32] = { // precalculated vector of angles and distances to display from player // DISPLAY_ANGLES_AND_DISTANCES(i).angle = the angle in radians from center os display of pixel located at center +/- i (not used in code) // DISPLAY_ANGLES_AND_DISTANCES(i).cosineAngle = cos(angle) // DISPLAY_ANGLES_AND_DISTANCES(i).sineAngle = sin(angle) // DISPLAY_ANGLES_AND_DISTANCES(i).distance = the distance in world units from player to the pixel in the display located at center +/- i {0, 65536, 0, 327680}, // ./calculate_display_angles.sh 5 15 distance from player to center of display = 5 world units, display width = 15 world units {3069, 65464, 3068, 328039}, {6126, 65249, 6117, 329116}, {9155, 64897, 9126, 330904}, {12146, 64413, 12077, 333390}, {15087, 63806, 14954, 336559}, {17967, 63088, 17743, 340393}, {20778, 62269, 20432, 344869}, {23512, 61363, 23011, 349962}, {26163, 60382, 25473, 355646}, {28726, 59340, 27815, 361893}, {31199, 58248, 30034, 368675}, {33579, 57119, 32129, 375962}, {35866, 55963, 34102, 383726}, {38060, 54791, 35956, 391939}, {40161, 53610, 37694, 400572}, {42172, 52428, 39321, 409600}, {44094, 51253, 40842, 418996}, {45931, 50088, 42262, 428736}, {47684, 48940, 43587, 438799}, {49358, 47810, 44822, 449161}, {50955, 46704, 45974, 459803}, {52480, 45622, 47048, 470705}, {53934, 44567, 48049, 481851}, {55322, 43539, 48982, 493223}, {56647, 42540, 49852, 504807}, {57912, 41570, 50664, 516587}, {59120, 40629, 51421, 528551}, {60274, 39717, 52129, 540687}, {61378, 38834, 52790, 552983}, {62433, 37979, 53408, 565429}, {63442, 37152, 53987, 578016} }; ... void TanksMainScreen::calculateRay(Vector &ray, fixedpoint_t &distToDisplay, int32_t x) { // x = -31..31 ray = this->player; fixedpoint_t cosine = 1; fixedpoint_t sine = 0; if (x < 0) { cosine = DISPLAY_ANGLES_AND_DISTANCES[-x].cosineAngle; sine = DISPLAY_ANGLES_AND_DISTANCES[-x].sineAngle; distToDisplay = DISPLAY_ANGLES_AND_DISTANCES[-x].distance; } else { cosine = DISPLAY_ANGLES_AND_DISTANCES[x].cosineAngle; sine = -DISPLAY_ANGLES_AND_DISTANCES[x].sineAngle; distToDisplay = DISPLAY_ANGLES_AND_DISTANCES[x].distance; } ray.rotate(cosine, sine); }
Y cómo queda el código que calcula el cambio del vector del jugador cuando éste se gira:
const Angle TanksMainScreen::ANGLES[16] = { // 16 angles (cosines and sines) for first quadrant (other quadrant values are calculated changing cos/sin signs) {65536, 0}, // ./calculate_dir_vector.sh 16 {65220, 6423}, {64276, 12785}, {62714, 19024}, {60547, 25079}, {57797, 30893}, {54491, 36409}, {50660, 41575}, {46340, 46340}, {41575, 50660}, {36409, 54491}, {30893, 57797}, {25079, 60547}, {19024, 62714}, {12785, 64276}, {6423, 65220} }; ... void TanksMainScreen::fillAngle(Angle &a, const uint8_t i) { if (i < 16) a = ANGLES[ i ]; else if ((i >= 16) && (i < 32)) { a.cosine = -ANGLES[i - 16].sine; a.sine = ANGLES[i - 16].cosine; } else if ((i >= 32) && (i < 48)) { a.cosine = -ANGLES[i - 32].cosine; a.sine = -ANGLES[i - 32].sine; } else if (i >= 48) { a.cosine = ANGLES[i - 48].sine; a.sine = -ANGLES[i - 48].cosine; } } ... void TanksMainScreen::rotatePlayer(RotateTo t) { if (t == RotateTo::LEFT) this->playerAngle = (this->playerAngle + 1) & 0x3F; // 0..63 else if (t == RotateTo::RIGHT) this->playerAngle = (this->playerAngle + 64 - 1) & 0x3F; // 0..63 Angle a; fillAngle(a, this->playerAngle); this->player.dir.x = a.cosine; this->player.dir.y = a.sine; }
Conclusión y siguiente entrega
El uso de raycasting combinado con el cálculo mediante aritmética de punto fijo permite a un microcontrolador de potencia muy limitada proyectar escenas básicas en 3D en tiempo real y poder disfrutar de una experiencia 3D aunque sea en una pequeña pantalla LCD de 128x64 pixels. En la siguiente entrega de esta serie relacionada con la consola GabrielBoy se abordará el diseño y la implementación del mítico juego Snake.
Todo el código y los diseños están en la sección soft.
[ añadir comentario ] ( 1036 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 1736 )
( 3 / 1736 )En esta segunda entrega de esta miniserie sobre el desarrollo de la GabrielBoy, se abordará el diseño y desarrollo del primero de los juegos: un tetris. Se parte del diseño original del tetris, que consiste en una cuadrícula de 10x20 posiciones en la que van cayendo piezas que el jugador debe ir colocando buscando que llenen filas enteras. No me pararé en explicar el juego porque todos los conocemos. Así que vamos a ello.
Mecánica del juego
Se trata de un tetris estándar: van apareciendo las piezas por arriba de forma aleatoria, con la cruceta movemos a los lados o hacemos que la pieza baje más rápido y con el botón A rotamos la pieza. Cuando conseguimos hacer una o varias líneas horizontales completas dichas líneas de borran del tablero y aumenta la velocidad de caida en función de la cantidad de líneas eliminadas. El jugador nunca "gana", las fichas siguen cayendo indefinidamente hasta que apaguemos la consola, reiniciemos o la última ficha en caer ya no quepa en el tablero porque este está lleno.
Diseño de la pantalla
La única pantalla que tiene el juego está gestionada por la clase TetrisMainScreen (en la carpeta games/tetris). Dibuja un tablero central, que alberga 10 x 20 huecos de 3 x 3 pixels cada uno (cada "cuadrado" del tetris es un bloque de 3 x 3 pixels). Con estas dimensiones tenemos un tablero que ocupa 30 x 60 pixels y que se coloca en el centro de la pantalla. Los huecos de los lados son de 49 pixels a izquierda y de 49 pixels a la derecha (49 + 30 + 49 = 128 pixels de anchura de la pantalla LCD).

El hueco de la izquierda se utiliza para indicar la siguiente figura que va a caer mientras que el hueco de la derecha se utiliza para indicar el nivel por el que se va: cada 5 filas eliminadas se sube de nivel y aumenta un 5% la velocidad de caida de las figuras. El nivel máximo es el 9 y a partir de ese nivel ya no se aumenta la velocidad de caida.
Mecánica interna
El código no trabaja con el framebuffer de la pantalla, sino que trabaja con una matriz de 10 x 20 enteros en la que cada elemento puede tener los siguientes valores:
0: hueco libre.
1: hueco ocupado por suelo.
2: hueco ocupado por una pieza que está aún cayendo
static const int32_t BOARD_WIDTH = 10; static const int32_t BOARD_HEIGHT = 20; static const int32_t BOARD_SIZE = BOARD_WIDTH * BOARD_HEIGHT; uint8_t board[BOARD_SIZE] __attribute__ ((aligned(4)));
Se define el tablero con el atributo "aligned(4)" de GCC para garantizar que el compilador aloja dicha variable en una dirección de memoria múltiplo de 4 bytes (32 bits), de esta manera las operaciones de inicialización y rrecorrido del tablero puede optimizarse un poco más. Las figuras están definidas en un array constante (en ROM) de 7 elementos y cada elemento del array (cada figura) es una matriz de 4x4 bytes.
class TetrisFigure { public: static const int32_t MAX_WIDTH = 4; static const int32_t MAX_SIZE = MAX_WIDTH * MAX_WIDTH; int32_t width; int32_t height; uint8_t data[MAX_SIZE] __attribute__ ((aligned(4))); TetrisFigure &operator = (const TetrisFigure &other); void rotateInto(TetrisFigure &other); void rotate(); }; ... const TetrisFigure TetrisMainScreen::FIGURES[7] = { { 4, 1, { 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 } }, { 3, 2, { 1, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0 } }, { 3, 2, { 0, 1, 1, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 } }, { 3, 2, { 1, 1, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0 } }, { 3, 2, { 1, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 } }, { 3, 2, { 0, 1, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0 } }, { 2, 2, { 1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 } } };
La figura que cae es una copia en RAM de la figura correspondiente de ese array, pues puede ser necesario rotarla. La rotación, como siempre es en pasos de 90 grados, se realiza por la técnica de la transposición y a continuación aplicar función espejo vertical u horizontal, y así no hay que hacer cálculos trigonométricos.
Máquina de estados
La máquina de estados consta de 3 estados:
1. NEW_FIGURE (estado inicial): En este estado se coge la figura siguiente y se intenta colocar en la parte superior del tablero para que vaya cayendo:
1.1. Si se puede colocar, se pasa al estado FALLING y se calcula una nueva figura para que sea la p2róxima siguiente".
1.2. Si no se puede colocar porque ya toca con suelo o con figuras anteriores "consolidadas", se pasa al estado GAME_OVER.
2. FALLING: Este es el estado principal del juego, la figura actual va cayendo y en el momento que se detecta que toca contra suelo o con borde inferior del tablero, la figura se convierte en suelo (se "consolida"). Cuando se detecta que se ha "generado suelo nuevo" se recorre el tablero, se eliminan las filas llenas y se comprueba si se debe subir de nivel.
2.1. Si la figura que está cayendo toca suelo, se pasa al estado NEW_FIGURE.
3. GAME_OVER: Por ahora es un estado "muerto". El juego se cuelga intencionadamente y el jugador debe reiniciar la consola si quiere seguir jugando o empezar de nuevo.
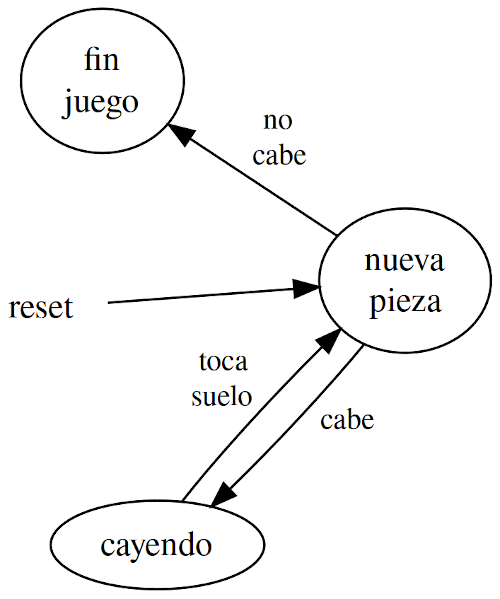
Screen *TetrisMainScreen::onUpdate() { bool boardChanged = false; uint8_t b = this->buttons.getValue(); LevelChanged levelChanged = LevelChanged::NO; if (this->status == St::NEW_FIGURE) { this->generateNewRandomFigure(); this->nextFigureChanged = true; this->figureX = this->rnd.getNextValue() % (10 - this->figure.width); this->figureY = 0; if (this->getFigureValidAt(this->figure, this->figureX, this->figureY)) { this->status = St::FALLING; this->ticksBetweenMovs = this->initialTicksBetweenMovs; boardChanged = true; } else { this->status = St::GAME_OVER; // game over is a dead state (console must be reseted) } } else if (this->status == St::FALLING) { this->ticksBetweenMovs--; if ((this->ticksBetweenMovs <= 0) || (b & Buttons::MASK_DOWN)) { if (this->getCanMoveFigureTo(Direction::DOWN)) { this->figureY++; } else { this->finalizeFigure(levelChanged); this->status = St::NEW_FIGURE; } if (this->ticksBetweenMovs <= 0) this->ticksBetweenMovs = this->initialTicksBetweenMovs; boardChanged = true; } else if ((b & Buttons::MASK_A) && this->getCanRotateFigure()) { this->figure.rotate(); boardChanged = true; } else if ((b & Buttons::MASK_LEFT) && this->getCanMoveFigureTo(Direction::LEFT)) { this->figureX--; boardChanged = true; } else if ((b & Buttons::MASK_RIGHT) && this->getCanMoveFigureTo(Direction::RIGHT)) { this->figureX++; boardChanged = true; } } if (boardChanged) { this->updateBoardWithFigure(); if (levelChanged == LevelChanged::YES) this->drawLevelLabel(); this->drawBoardWithFigureOnFrameBuffer(); if (this->nextFigureChanged) { this->drawNextFigureOnFrameBuffer(); this->nextFigureChanged = false; } this->display.notifyFrameBufferChanged(); } return nullptr; }
Siguiente entrega
En la siguiente entrega se analizará el segundo de los juegos que incluye la consola. Un shooter 3D muy sencillo implementado con la técnica del raycasting
Todo el código y los diseños están en la sección soft.
[ añadir comentario ] ( 890 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 1745 )
( 3 / 1745 )A lo largo de 4 entradas consecutivas en el blog iré detallando todo el desarrollo y la implementación de una miniconsola de videojuegos portátil que he desarrollado para mi hijo. La idea era hacer una consola al estilo "maquinita" o "game & watch" pero algo más elaborada, alimentada con batería recargable y con algunos juegos prefijados. En esta entrada me centraré en el diseño hardware y el desarrollo de las librerías básicas para acceso al hardware.
Características principales
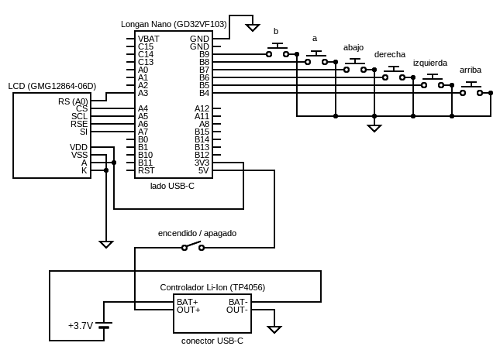
- Microcontrolador GD32VF103: núcleo RISC-V de 32 bits a 96 MHz, con 256 Kb de Flash y 32 Kb de SRAM.
- Pantalla: Módulo GMG12864 basado en el controlador de display ST7565 de 128x64 pixels en blanco y negro (sin escalas de grises, cada pixel encendido o apagado).
- Botonera: Cruceta (arriba, abajo, izquierda y derecha) más dos botones adicionales (A y B) de funcionalidad personalizable.
- Alimentación: Batería de una celda de LiPo o LiIon de 1200 mAh (3.7 voltios) para unas 6 horas de juego continuado. Recargable mediante módulo de controlador de carga con conector USB-C y con interruptor de encendido.
A continuación una foto del frontal de la consola (encendida aunque aún sin caja).

Y de la parte trasera, donde se puede ver todo el trabajo de soldadura (a muchos técnicos en electrónica seguramente les sangrarán los ojos, pero bueno, hice lo que pude, se me da mejor programar que soldar).

Pantalla
Aprovechando que el microcontrolador tiene una potencia razonable se opta por un modelo de pantalla con una capa de abstracción basada en framebuffer, de tal manera que los juegos de la consola escribirán en un framebuffer de lineal de $128 \times 64 = 8192$ bytes. Para encender o apagar el pixel (x, y) se escribirá un 1 o un 0, respectivamente, en el offset $\left( y \times 128 \right) + x$ del framebuffer:
frameBuffer[(y * 128) + x] = 1; // encender pixel (x, y) frameBuffer[(y * 128) + x] = 0; // apagar pixel (x, y)
Habrá una clase encargada de traducir la información del framebuffer en transferencias SPI al módulo GMG12864 para que se pinte de forma adecuada la pantalla. Esta abstracción nos permite adaptarnos a pantallas futuras y no depender sólo de esa pantalla en concreto, además de que facilita el desarrollo y las pruebas como veremos más adelante.
Botonera
La botonera se implementa con 6 botones mecánicos con el común a masa. Las 6 entradas GPIO en el microcontrolador se configuraon como GPIOs en pullup y así nos ahorramos tener que poner resistencias de pull-up por fuera. Se opta por no poner circuitería antirrebote en los botones para abaratar costes: el antirrebote se realizará por software, mediante una máquina de estados que, con temporizadores, evitará que se produzcan rebotes en la acción de las teclas.
Alimentación
La alimentación es muy sencilla, se utiliza un módulo TP4056 para una celda LiPo o LiIon de 3.7 voltios que ya viene con conector USB-C para carga y salida estabilizada que puede ir directa a la entrada de 5 voltios del módulo del microcontrolador. Toda la consola requiere 3.3 voltios para funcionar pero, como el convertidor de voltaje de la placa del microcontrolador tiene un dropout muy bajo, se pueden meter los 3.7 voltios de salida de la controladora de carga por la entrada de 5 voltios de la placa del microcontrolador. El interruptor de alimentación se coloca en serie con la alimentación que llega al microcontrolador y a la pantalla de tal manera que, aunque el interruptor de la consola esté apagado, su batería se podrá cargar con un cargador estándar USB-C.
Entorno de desarrollo y clases básicas
Como otros desarrollos "grandes" que he hecho siempre intento que el proceso de desarrollo y de depuración sean lo más eficientes posibles y para ello trato siempre de aprovechar el uso de clases abstractas para abstraer el código del hardware específico o la plataforma en la que estoy trabajando. Por ejemplo, para el manejo de la pantalla habrá una clase "Display" que albergará el framebuffer y algunas funciones miembro auxiliares, a continuación se crea una carpeta "gd32vf103" donde irá la implementación específica para el microcontrolador y la pantalla utilizadas "SPIGMG12864Display" que heredará de "Display". Se crea también una carpeta "linux" donde va la implementación específica para Xlib ("XlibDisplay").
A continuación los diagramas de clases de las clases principales del código fuente:
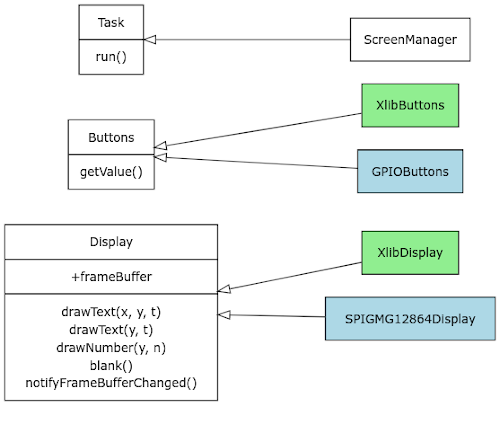
En azul las clases específicas del microcontrolador, en verde las clases específicas de linux y en blanco las clases comunes.
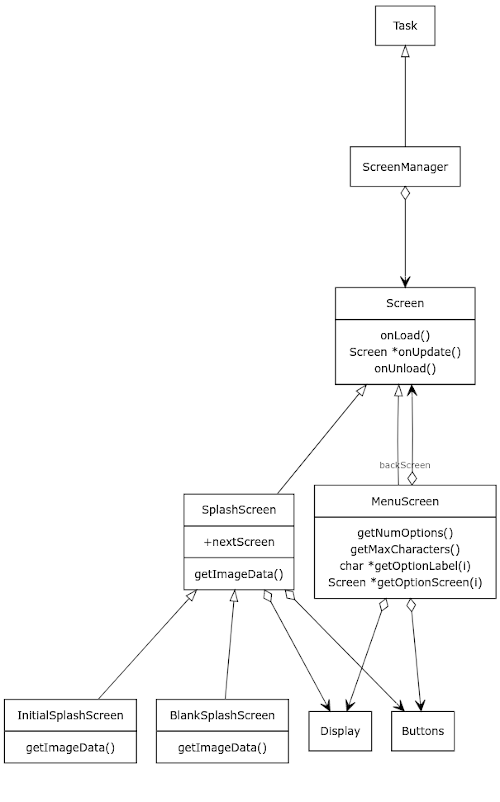
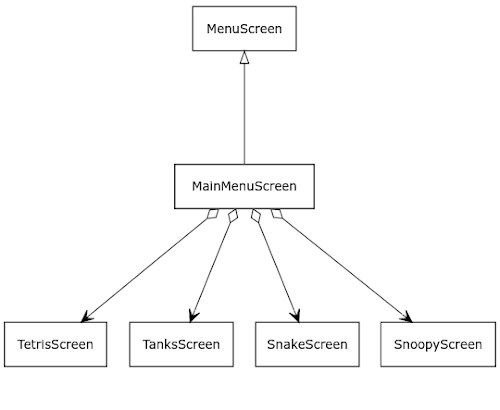
En estos diagramas de clases se pueden ver las clases básicas que constituyen el "framework" de la miniconsola. El elemento central para entender cómo funciona el flujo del software es la clase "Screen" que representa una pantalla (título, menú, un juego en sí, etc.) y la clase "ScreenManager", encargada de ir cambiando de pantallas en función de las necesidades del flujo del programa.
Cada Screen debe implementar las funciones miembro:
void Screen::onLoad(InterScreenData *dataFromPreviousScreen): Esta función se invoca cuando se carga una pantalla, se supone que a partir de este momento el framebuffer es "suyo" por lo que lo lógico en esta función miembro es que se inicialicen variables, se borre el framebuffer, se pinten las partes fijas del mismo, se inicialice la mecánica de esta pantalla, etc.
Screen *Screen::onUpdate(): Esta función se ejecuta cada 20 ms por parte del timer del sistema para que se implementen la mecánica de la pantalla (menú, juego, etc.). Si devuelve *this o nullptr significará que no hay que cambiar de pantalla, en caso contrario significa que queremos cambiarnos a la pantalla correspondiente.
InterScreenData *Screen::onUnload(): Esta función miembro se ejecuta en caso de que la última llamada a "onUpdate()" haya devuelto una "Screen *" válida (no nullptr) y diferente a la actual. La idea es poner aquí código de "terminación" de nuestra pantalla. Un objeto de clase "Screen" puede ser cargado ("onLoad") y descargado ("onUnload") varias veces entre su construcción y su destrucción.
La clase "ScreenManager" heredará de la clase "Task" para implementar la función miembro run, donde se realizará la mecanica del onLoad/onUpdate/onUnload indicada:
class InterScreenData { }; class Screen; class Screen { public: virtual void onLoad(InterScreenData *dataFromPreviousScreen) = 0; virtual Screen *onUpdate() = 0; virtual InterScreenData *onUnload() = 0; }; class ScreenManager : public Task { public: Screen *currentScreen; ScreenManager(Screen &initialScreen, InterScreenData *initialInterScreenData); virtual void run(); }; ScreenManager::ScreenManager(Screen &initialScreen, InterScreenData *initialInterScreenData) : currentScreen(&initialScreen) { this->currentScreen->onLoad(initialInterScreenData); } void ScreenManager::run() { Screen *nextScreen = this->currentScreen->onUpdate(); if ((nextScreen != this->currentScreen) && (nextScreen != nullptr)) { InterScreenData *isd = this->currentScreen->onUnload(); nextScreen->onLoad(isd); this->currentScreen = nextScreen; } }
Como se puede ver es una mecánica muy sencilla. A partir de la clase "Screen" se crean todas las pantallas de la aplicación, por ejemplo:
- SplashScreen: Pantalla de bienvenida con una imagen de fondo y un texto de copyright que espera a que pulses un botón para pasar a la siguiente pantalla.
- MenuScreen: Pantalla de menú que permite, a su vez, especializarse para crear diferentes menus (como MainMenuScreen).
- ...
Cualquier clase que herede de Screen y que implemente los tres métodos especificados será otro tipo de pantalla con la funcionalidad que queramos.
Esta forma de programar la aplicación es muy escalable y permite crear fácilmente flujos de código muy elaborados:
int main() { // init hardware interruptInit(); RGBLed::init(); GPIOButtons buttons; Random random(buttons); SPIGMG12864Display display; display.blank(); // create screens InitialSplashScreen initialSplashScreen(display, buttons); MainMenuScreen mainMenuScreen(display, buttons); TetrisMainScreen tetrisMainScreen(display, buttons, random); TanksMainScreen tanksMainScreen(display, buttons, random); SnakeMainScreen snakeMainScreen(display, buttons, random); SnoopyMainScreen snoopyMainScreen(display, buttons, random); // link screens initialSplashScreen.setNextScreen(mainMenuScreen); mainMenuScreen.setBackScreen(initialSplashScreen); mainMenuScreen.setTetrisScreen(tetrisMainScreen); mainMenuScreen.setTanksScreen(tanksMainScreen); mainMenuScreen.setSnakeScreen(snakeMainScreen); mainMenuScreen.setSnoopyScreen(snoopyMainScreen); // main loop ScreenManager m(initialSplashScreen, nullptr); MyListener myListener(display, buttons, m); Timer::init(myListener, 20_msForTimer); while (true) asm volatile ("wfi"); }
No se usan variables globales (no son necesarias):
1. Se inicializa el hardware: el controlador de interrupciones, la pantalla, la botonera y el generador de números pseudoaleatorios.
2. Se construyen todas las pantallas: A todas les pasamos el objeto display y el objeto buttons (a algunas de ellas se les pasa el generador del números pseudoaleatorios).
3. Se enlazan las pantallas: Cada objeto de clase Screen debe tener los punteros a las pantallas hacia las que puede irse a partir de él. Por ejemplo, la pantalla initialSplashScreen debe saber que debe ir a la pantalla mainMenuScreen cuando pulsen un botón. De la misma forma la pantalla de menú, que debe saber a qué pantalla se salta con cada opción.
4. Justo antes del bucle principal: Se le indica al ScreenManager cual es pantalla inicial (la que debe aparecer en el arranque).
5. Bucle principal: En este caso, para ahorrar energía, no se hace el típico bucle "while (true)" sino que se programa el timer del sistema para dispararse cada 20 milisegundos y en la función miembro "timerExpired" del objeto escuchador del timer, se invoca la máquina el "run" de los botones y el "run" del ScreenManager, que es la función miembro encargada de gestionar las pantallas (llamar a onLoad/onUpdate/onUnload de las pantallas). Haciendo el bucle principal podemos utilizar la instrucción ensamblador "wfi" (wait for interrupt) para que, entre iteraciones, el procesador pueda dormirse y así evitar que se consuma mucha batería.

Siguiente entrega
En la siguiente entrega se analizará el diseño y la implementación del Tetris (uno de los cuatro juegos que incluye la miniconsola).
Todo el código y los diseños están en la sección soft.
[ añadir comentario ] ( 1116 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 1792 )
( 3 / 1792 )Al igual que se hizo en una anterior entrega con el SoC Allwinner H5, un ARM Cortex-A53 (64 bits), esta vez toca hacer prueba de concepto de bare metal con el SoC Allwinner D1, uno de los más utilizados en placas tipo SBC basadas en RISC-V. El D1 es un RISC-V de 64 bits que tiene un mecanismo de arranque muy parecido al usado por los otros SoCs de Allwinner. Programar a nivel bare metal un SoC de estas características tiene poco sentido práctico más allá de la experimentación, de hecho para aplicaciones serias siempre es recomendable utilizar un RTOS o un Linux, pero pelearse con las interioridades de un SoC a nivel bare metal permite aprender mucho sobre estos chips y sobre las secuencias de arranque de los procesadores en general.
MangoPi
En este caso, se utilizará una placa Mango Pi, con un tamaño muy parecido a la RPi Zero, pero que utiliza un SoC D1, aunque la prueba descrita en este post se podrá realizar en cualquier SBC que utilice un SoC D1.
Secuencia de arranque del D1
Se recomienda echar un vistazo al post anterior donde se aborda el mismo objetivo, pero con el SoC Allwinner H5 (un ARM Cortex-A53). Al igual que el SoC H5 y otros SoCs de Allwinner, lo que hace el procesador cuando arranca es, básicamente:
1.- Copiar el contenido de los primeros 32 Kbytes que empiezan en el sector 16 de la tarjeta de memoria en una zona de la memoria estática interna (más info).
2.- Comprobar el checksum del código, calculado en la cabecera de esos 32 Kbytes (más info).
3.- Si el checksum es correcto, ejecuta la primera instrucción de esos 32 Kbytes (que suele ser una instrucción de salto "jal", por lo que el código de arranque en sí normalmente se coloca justo después de la cabecera de esos 32 Kbytes).
La secuencia es igual a la utilizada en los SoC ARM de Allwinner (como el H5) con la única diferencia de que la instrucción de salto (los 4 primeros bytes de ese bloque) se codifican como la instrucción "jal" de RISC-V (es la misma instrucción tanto para RV32I como para RV64I).
A continuación puede verse el código máquina correspondiente a la instrucción "jal" (Jump And Link) de RISC-V que se coloca en los 4 primeros bytes de la cabecera:
bit bit
31 ......................... 12 +--rd---+ 6 5 4 3 2 1 0
imm[20|10:1|11|19:12] 0 0 0 0 0 1 1 0 1 1 1 1
\-------/ \-----------/
| |
| +-------- opcode
+-------------------- reg destino
(en r0 se guarda la
dirección de la
siguiente instrucción
a "jal")
"imm" es el offset al cual debe saltarse (en complemento a 2, puede ser un valor negativo). Nótese que el valor de "imm" es de 21 bits pero se descarta el bit menos significativo, puesto que el código en RISC-V siempre debe alojarse en direcciones pares de memoria.
Parchear la herramienta mksunxiboot
La herramienta mksunxiboot se encarga de calcular la cabecera con el correspondiente checksum para que el SoC arranque correctamente el código que queramos. Es un código en C muy sencillo que compilamos y ejecutamos en el ordenador, recibe como entrada un fichero ".bin" con el código de arranque y genera un ".bin" con el código de arranque precedido con la cabecera necesaria (con el checksum dentro) para que el SoC reconozca como "correcto" el código y lo ejecute.
La herramienta original está diseñada para SoCs ARM así que para adecuarla al D1 sólo hace falta cambiar la instrucción de salto para que, en lugar de ser una instrucción de salto ARM, sea una instrucción de salto RISC-V.
En "mksunxiboot.c" se sustituye el siguiente código:
img.header.jump_instruction = /* b instruction */ 0xEA000000 | /* jump to the first instruction after the header */ ( (sizeof(boot_file_head_t) / sizeof(int) - 2) & 0x00FFFFFF );
Por este otro:
u32 code_offset = sizeof(boot_file_head_t); img.header.jump_instruction = /* risc-v "jal" instruction */ (((code_offset >> 20) & 1) << 31) | (((code_offset >> 1) & 0x3FF) << 21) | (((code_offset >> 11) & 1) << 20) | (((code_offset >> 12) & 0xFF) << 12) | 0x00000006F;
Y ya está, compilando con:
gcc -o mksunxiboot mksunxiboot.c
Tenemos nuestra herramienta preparada para "firmar" nuestro código RISC-V para el D1.
SPL
En terminología Allwinner, el SPL (o Second Program Loader) es como se llama al código que se ejecuta justo después de la ROM del D1 (el que se le pasa a "mksunxiboot" para que lo firme) y que es el código que se pone en la tarjeta de memoria justo a continuación de la cabecera que calcula "mksunxiboot".
; sector 16 de la tarjeta de memoria
jal @inicioCódigoSPL ; primeros 4 bytes de la cabecera
... resto de la cabecera calculada por la utilidad "mksunxiboot" ...
@inicioCódigoSPL:
... nuestro código de arranque o SPL ...
Haremos un SPL extremadamente sencillo que se limite a hacer parpadear un pin GPIO al que se le conecta un LED.
#include <stdint.h> void spl() __attribute__ ((naked, section(".spl"))); #define WAIT 40000000ULL #define GPIO_BASE 0x02000000 #define PC_CFG *((uint32_t *) (GPIO_BASE + 0x0060)) #define PC_DAT *((uint32_t *) (GPIO_BASE + 0x0070)) #define PC_PULL0 *((uint32_t *) (GPIO_BASE + 0x0084)) void spl() { PC_CFG = (PC_CFG & 0xFFFFFF0F) | 0x00000010; // PC1 = output PC_PULL0 = (PC_PULL0 & 0xFFFFFFF3) | 0x00000008; // PC1 = pull-down while (true) { PC_DAT |= 0x00000002; // PC1 = 1 for (uint64_t n = 0; n < WAIT; n++) ; PC_DAT &= 0xFFFFFFFD; // PC1 = 0 for (uint64_t n = 0; n < WAIT; n++) ; } }
Como se puede comprobar, el código no hace uso de variables globales ni de llamadas a funciones o librerías, para que sea autocontenido y no genere dependencias externas. Algunos aspectos importantes:
- El nombre de la función es irrelevante, no tiene por qué ser "main". De hecho el código no se enlazará, sólo se compilará.
- Mediante atributos, indicamos al compilador que el código de la función debe alojarse en una sección llamada ".spl" (nombre arbitrario) y que debe ser "naked" (el compilador no generará código de preámbulo o postámbulo, ya que es una función a la que se llega con un salto, no con una llamada).
- El código simplemente inicializa la línea GPIO correspondiente al pin PC1 (el pin número 22 del conector de 40 pines de la Mango Pi), como un GPIO de salida y a continuación se queda en un bucle infinito emitiendo un 1 y un 0 alternativamente, para que pueda parpadear un led conectado a PC1.
Una vez compilado (generado el fichero "spl.o"), se utiliza la utilidad "objcopy" para extraer el código de la sección ".spl" y meterlo en un fichero binario crudo "spl.bin". A continuación, este fichero "spl.bin" es pasado por la utilidad "mksunxiboot" que modificamos anteriormente, para que genere otro "spl_with_signature.bin" que estará firmado y, por tanto, podrá ya ser ejecutado por el D1.
riscv64-none-elf-g++ -mtune=thead-c906 -fno-exceptions -fno-rtti -nostartfiles -c -o spl.o spl.cc riscv64-none-elf-objcopy -O binary -j .spl spl.o spl.bin ./mksunxiboot spl.bin spl_with_signature.bin
El último paso consiste en grabar este fichero "spl_with_signature.bin" directamente en el sector 16 de una tarjeta de memoria (nótese que cada sector en una tarjeta de memoria mide 512 bytes, por tanto el sector 16 es el offset 8192 = 1024 * 8 a nivel de byte):
dd if=spl_with_signature.bin of=/dev/sdX bs=1024 seek=8
Si colocamos un LED entre PC1 y masa (usar siempre una resistencia en serie) y arrancamos el D1 con la tarjeta de memoria que acabamos de tostar, podremos ver nuestro blinker bare metal en acción.

Todo el código en la sección soft.
[ añadir comentario ] ( 1475 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 2.9 / 1644 )
( 2.9 / 1644 )Para la generación de números aleatorios en circuitos digitales existen, principalmente, dos opciones: por un lado el uso de LFSRs (registros de desplazamiento con realimentación lineal) de ciclo maximal, que son circuitos deterministas con los que se obtienen números pseudoaleatorios, y, por otro lado, el uso de algún parámetro físico que realmente tenga un comportamiento ruidoso y nos permita extraer números de él, algo que no sea determinista. La primera opción es la que he utilizado siempre hasta ahora pero con la excusa del montaje del Belén de este año, se propone la implementación de un generador de números "verdaderamente" aleatorios (TRNG) para generar el brillo del firmamento del Belén. El resultado visual es el de siempre, la diferencia es que la secuencia de brillos es realmente aleatoria.
Objetivo
La idea es la misma de años anteriores: generar destellos aleatorios en un firmamento artificial hecho de Leds blancos para el montaje del Belén. Debido a que la secuencia de destellos no tiene por qué ser "realmente" aleatoria, hasta ahora nos bastaba con un generador de números pseudoaleatorios implementado con un LFSR de ciclo maximal (un puñado de biestables y una función de transición basada en dos o tres puertas lógicas, poco más).
Los LFSRs son, por definición, deterministas, no existe ninguna "magia" en ellos, lo que sucede es que la secuencia de números que generan es lo suficientemente "extraña" y aparentemente no determinista, como para que, a ojos de un observador humano, parezca que realmente se están generando números totalmente aleatorios. En este post se hace una introducción y una explicación muy completa sobre el fundamento, uso e implementación de LFSRs en circuitos digitales.
Buscar una fuente de ruido
En nuestro caso, si queremos generar números verdaderamente aleatorios, debemos buscar una fuente de ruido físico que podamos traducir en una secuencia de números (o, al menos, en una secuencia aleatoria de 0s y 1s). Una primera aproximación electrónica podría ser implementar un ADC y leer mediante ese ADC alguna fuente de ruido electrónico analógico.
Una buena opción en este sentido es aprovechar la característica de ruido de que se produce de forma natural en los transistores de unión cuando se polariza la unión base-emisor de forma inversa, dejando el colector al aire.
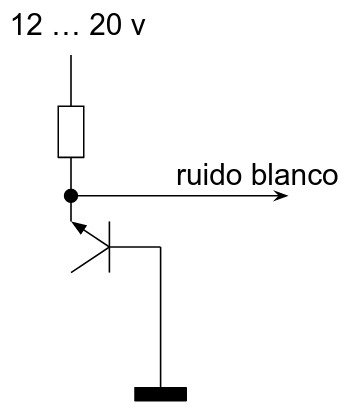
Esta características de los transistores de unión es bien conocida y muy usada en generadores de ruido analógicos, ya que el ruido que genera se asemeja mucho al ruido blanco y no requiere una excesiva calibración.
En el caso de que necesitemos generar números aleatorios de esta manera debemos colocar un ADC para leer el ruido que genere el transistor y ya tendríamos nuestro TRNG. Esta aproximación es correcta pero engorrosa y costosa por las siguientes razones:
- Requiere de circuitería analógica: no siempre podremos disponer de ella y es algo más delicada siempre a la hora de diseñarla, calibrarla y testearla.
- Requiere de un ADC: Los ADCs son recursos caros, incluso aunque los implementemos en forma de delta-sigma, consumen recursos y siempre requieren de una parte de electrónica analógica que, como se comentó antes, requiere más calibración, testeo y cuidado en el diseño.
La pregunta que surge es ¿Habría posibilidad de encontrar una fuente de ruido dentro de un circuito digital de tal forma que nos permita implementar un TRNG directamente en una FPGA o en un ASIC? Lo cierto es que sí y no es nada complicado.
Oscilador en anillo
Un oscilador en anillo es un tipo especial de oscilador digital formado por un bucle cerrado de una cantidad impar de inversores.
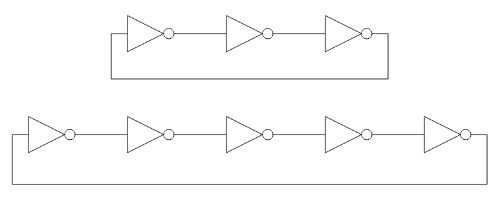
Como se puede comprobar, al haber una cantidad impar de inversores, el circuito será aestable y la oscilación que se genera (en cualquiera de sus inversores) tendrá una frecuencia inversamente proporcional a la suma de los tiempos de propagación de todas las puertas inversoras. Hasta aquí parece un oscilador más, pero lo cierto es que, al ser un oscilador no sintonizado (no se utiliza un cristal de cuarzo para mantener una frecuencia estable, como los osciladores "reales" que se utilizan habitualmente en los circuitos digitales) la frecuencia y ciclo de trabajo dependerá del tiempo de propagación de las puertas lógicas y este tiempo de propagación nunca es fijo, dependerá de:
- La tecnología de fabricación.
- La distancia en el sustrato que haya entre la salida de una puerta y la entrada de la puerta siguiente.
- Las impurezas en el sustrato (siempre las hay).
- La temperatura.
- Radiación electromagnética externa que afecte al circuito.
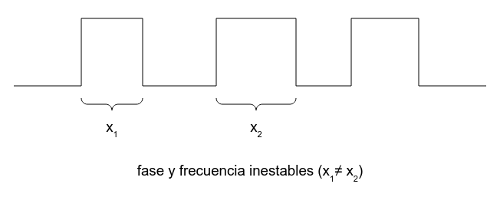
Por eso los fabricantes de circuitos digitales nunca dan un tiempo exacto de propagación de puerta, dan un rango (para un rango determinado de temperatura y de condiciones determinadas). Es este jittering (desplazamiento de fase y/o de frecuencia) que se produce en estos osciladores lo que podemos aprovechar como fuente de ruido.
Extraer el ruido de jittering
Si definimos dos o más osciladores en anillo "teóricamente" iguales (por ejemplo con la misma cantidad de puertas y aunque compartan sustrato, en la misma FPGA o ASIC), lo cierto es que acabarán desfasándose unos con otros de forma aleatoria debido a las razones anteriormente citadas. En el paper An embedded true random number generator for FPGAs (Kohlbrenner P. y Gaj K., 2004) se introduce esta técnica y se plantea un circuito auxiliar muestrador que permite obtener una secuencia de bits muy próxima a una distribución uniforme (ruido blanco). Yo he simplificado mucho dicho muestreador: no genera una secuencia de distribución uniforme pero para el caso que nos ocupa cumple su cometido correctamente ya que lo único que hago es muestrear la función XOR entre la salida de ambos osciladores en anillo y meter el bit resultante en un registro de desplazamiento.
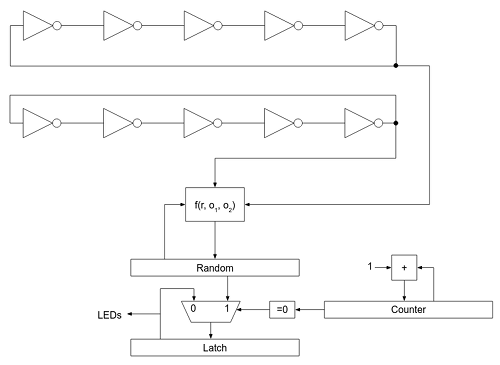
El código VHDL asociado sería el siguiente:
library ieee; use ieee.std_logic_1164.all; use ieee.numeric_std.all; entity Max1000TRNG is port ( ClkIn : in std_logic; Led1Out : out std_logic; Led2Out : out std_logic; Led3Out : out std_logic; Led4Out : out std_logic; Led5Out : out std_logic; Led6Out : out std_logic; Led7Out : out std_logic; Led8Out : out std_logic; Star1Out : out std_logic; Star2Out : out std_logic; Star3Out : out std_logic; Star4Out : out std_logic; Star5Out : out std_logic; Star6Out : out std_logic; Star7Out : out std_logic; Star8Out : out std_logic ); end entity; architecture A of Max1000TRNG is signal CounterD : std_logic_vector(23 downto 0); signal CounterQ : std_logic_vector(23 downto 0); signal FreeOsc1A : std_logic; signal FreeOsc1B : std_logic; signal FreeOsc1C : std_logic; signal FreeOsc1D : std_logic; signal FreeOsc1E : std_logic; signal FreeOsc2A : std_logic; signal FreeOsc2B : std_logic; signal FreeOsc2C : std_logic; signal FreeOsc2D : std_logic; signal FreeOsc2E : std_logic; attribute keep : boolean; attribute keep of FreeOsc1A : signal is true; attribute keep of FreeOsc1B : signal is true; attribute keep of FreeOsc1C : signal is true; attribute keep of FreeOsc1D : signal is true; attribute keep of FreeOsc1E : signal is true; attribute keep of FreeOsc2A : signal is true; attribute keep of FreeOsc2B : signal is true; attribute keep of FreeOsc2C : signal is true; attribute keep of FreeOsc2D : signal is true; attribute keep of FreeOsc2E : signal is true; signal RandomD : std_logic_vector(7 downto 0); signal RandomQ : std_logic_vector(7 downto 0); signal LatchD : std_logic_vector(7 downto 0); signal LatchQ : std_logic_vector(7 downto 0); begin process (ClkIn) begin if (ClkIn'event and (ClkIn = '1')) then CounterQ <= CounterD; RandomQ <= RandomD; LatchQ <= LatchD; end if; end process; -- free oscillator 1 FreeOsc1A <= not(FreeOsc1E); FreeOsc1B <= not(FreeOsc1A); FreeOsc1C <= not(FreeOsc1B); FreeOsc1D <= not(FreeOsc1C); FreeOsc1E <= not(FreeOsc1D); -- free oscillator 2 FreeOsc2A <= not(FreeOsc2E); FreeOsc2B <= not(FreeOsc2A); FreeOsc2C <= not(FreeOsc2B); FreeOsc2D <= not(FreeOsc2C); FreeOsc2E <= not(FreeOsc2D); -- random bit generated from jittering between free oscillators RandomD <= RandomQ(6 downto 0) & (FreeOsc1A xor FreeOsc2A); -- latch the random number every time counter overflows CounterD <= std_logic_vector(unsigned(CounterQ) + 1); LatchD <= RandomQ when (CounterQ = std_logic_vector(to_unsigned(0, 24))) else LatchQ; Led1Out <= LatchQ(0); Led2Out <= LatchQ(1); Led3Out <= LatchQ(2); Led4Out <= LatchQ(3); Led5Out <= LatchQ(4); Led6Out <= LatchQ(5); Led7Out <= LatchQ(6); Led8Out <= LatchQ(7); Star1Out <= LatchQ(0); Star2Out <= LatchQ(1); Star3Out <= LatchQ(2); Star4Out <= LatchQ(3); Star5Out <= LatchQ(4); Star6Out <= LatchQ(5); Star7Out <= LatchQ(6); Star8Out <= LatchQ(7); end architecture;
Nótese el uso de la palabra reservada "attribute" para definir un atributo booleano llamado "keep" asociado a las señales de los osciladores en anillo. Este atributo se utiliza para indicarle al entorno de desarrollo que no simplifique la función booleana y que mantenga ("keep") las señales indicadas, aunque al entorno le parezcan "desechables". Mediante este truco obligamos al entorno de desarrollo a implementar los osciladores en anillo con el número exacto de puertas que necesitamos.

Como siempre, el código fuente puede descargarse de la sección soft.
¡Feliz Navidad!
[ añadir comentario ] ( 3129 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3.4 / 2719 )
( 3.4 / 2719 )
 Calendario
Calendario




