FPGA
La FPGA que se ha usado es una Xilinx Spartan 3E, que se puede encontrar en la placa Papilio One (http://papilio.cc). Esta placa es open hardware, con interface USB, memoria flash SPI para almacenar la configuración del hardware y con una buena relación calidad/precio (unos 38 dólares aproximadamente).
El entorno de desarrollo de Xilinx es un poco complejo (muchas opciones) pero se le coge el truco rápido. Es gratuito (aunque no es software libre) y muy fácil de instalar tanto en Windows como en Linux (no está para Mac). El entorno de desarrollo permite gestionar proyectos en VHDL o Verilog y generar al final los ficheros ".bit" que son los que se mandan a la FPGA.
De http://papilio.cc se descarga el Papilio Loader, un software open source que permite "tostar" los ficheros ".bit" en la placa FPGA y probar los diseños rápidamente. En la propia página del proyecto vienen varios tutoriales.
Prueba de concepto
Como prueba inicial se plantea un circuito conversor de binario (4 bits, del 0 al 9) a 7 segmentos mediante interfaz serie:
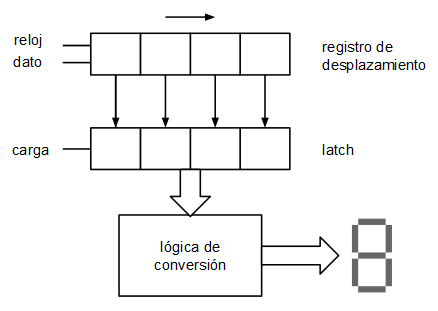
Se trata de un esquema muy sencillo: un registro de desplazamiento de 4 bits (que permite leer la entrada serie), un latch de 4 bits que carga el contenido del registro de desplazamiento y a la salida del latch una lógica combinatoria que convierte el número de 4 bits en una salida de 7 bits (para el display de 7 segmentos).
VHDL de la lógica combinatoria
VHDL es un lenguaje de descripción de hardware, no un lenguaje imperativo al uso. Cada línea de código describe un comportamiento y la única forma de realizar procesamiento secuencial es mediante la cláusula "process" ya que por defecto se ejecuta "todo a la vez".
Una lógica combinatoria está basada en puertas lógicas y las puertas lógicas se "ejecutan" siempre, no son como los biestables u otros elementos secuenciales. Para la lógica combinatoria de conversión binario a 7 segmentos se puede utilizar la sentencia WHEN...ELSE:
B(0) <= '1' when ((x = "0000") or (x = "0001") or (x = "0011") or (x = "0100") or (x = "0101") or (x = "0110") or (x = "0111") or (x = "1000") or (x = "1001")) else '0'; B(1) <= '1' when ((x = "0000") or (x = "0010") or (x = "0011") or (x = "0101") or (x = "0110") or (x = "1000") or (x = "1001")) else '0'; B(2) <= '1' when ((x = "0000") or (x = "0010") or (x = "0110") or (x = "1000")) else '0'; B(3) <= '1' when ((x = "0000") or (x = "0010") or (x = "0011") or (x = "0101") or (x = "0110") or (x = "0111") or (x = "1000") or (x = "1001")) else '0'; B(4) <= '1' when ((x = "0000") or (x = "0001") or (x = "0010") or (x = "0011") or (x = "0100") or (x = "0111") or (x = "1000") or (x = "1001")) else '0'; B(5) <= '1' when ((x = "0000") or (x = "0100") or (x = "0101") or (x = "0110") or (x = "1000") or (x = "1001")) else '0'; B(6) <= '1' when ((x = "0010") or (x = "0011") or (x = "0100") or (x = "0101") or (x = "0110") or (x = "1000") or (x = "1001")) else '0';
Como se puede apreciar en este caso, las 7 líneas de código debe "ejecutarse" de forma concurrente. Dicho de otra forma: se describen 7 circuitos combinacionales que deben implementarse en paralelo.
En este caso x es la salida del latch mientras que B es la salida de la FPGA que está conectada al display de 7 segmentos. En este caso se ha usado un display de cátodo común por lo que para encender un segmento del display hay que emitir un ‘1’ en la salida correspondiente.
VHDL de la lógica secuencial
La lógica secuencial se divide en la lógica del registro de desplazamiento que se ha implementado utilizando el clásico modelo RTL:
d_reg <= data_in & q_reg(3 downto 1); --d_reg es q_reg desplazado concatenado con el bit que hay en data_in process(clock_in) --el proceso se activa cuando clock_in cambia begin if (rising_edge(clock_in)) then --cuando hay un flanco de subida q_reg <= d_reg; --se carga d_reg en q_reg end if; end process;
Y la lógica del latch de 4 bits, que se encarga de cargar el registro de desplazamiento (q_reg) en la señal de entrada de la lógica combinatoria para la salida de 7 segmentos (x), y que también se ha implementado utilizando el modelo RTL:
process(latch_in) --el proceso se activa cuando latch_in cambia begin if (rising_edge(latch_in)) then --cuando hay un flanco de subida x <= q_reg; --se carga q_reg en x end if; end process;
En este caso las acciones a realizar no se hacen "siempre" sino que dependen de otras señales (clock_in y latch_in) y debe hacerse una evaluación secuencial (si ocurre esto entonces aquello), por eso se utilizan bloques "process". Nótese que ambos bloques "process" se "ejecutan" en paralelo.
VHDL completo
El código VHDL completo, incluyendo la arquitectura y el port queda como sigue:
library IEEE; use IEEE.STD_LOGIC_1164.ALL; use IEEE.STD_LOGIC_ARITH.ALL; use IEEE.STD_LOGIC_UNSIGNED.ALL; entity SimpleShiftRegister is port ( clock_in : in std_logic; data_in : in std_logic; latch_in : in std_logic; B : out std_logic_vector(6 downto 0) ); end SimpleShiftRegister; architecture behavioral of SimpleShiftRegister is signal d_reg : std_logic_vector(3 downto 0); signal q_reg : std_logic_vector(3 downto 0); signal x : std_logic_vector(3 downto 0); begin d_reg <= data_in & q_reg(3 downto 1); B(0) <= '1' when ((x = "0000") or (x = "0001") or (x = "0011") or (x = "0100") or (x = "0101") or (x = "0110") or (x = "0111") or (x = "1000") or (x = "1001")) else '0'; B(1) <= '1' when ((x = "0000") or (x = "0010") or (x = "0011") or (x = "0101") or (x = "0110") or (x = "1000") or (x = "1001")) else '0'; B(2) <= '1' when ((x = "0000") or (x = "0010") or (x = "0110") or (x = "1000")) else '0'; B(3) <= '1' when ((x = "0000") or (x = "0010") or (x = "0011") or (x = "0101") or (x = "0110") or (x = "0111") or (x = "1000") or (x = "1001")) else '0'; B(4) <= '1' when ((x = "0000") or (x = "0001") or (x = "0010") or (x = "0011") or (x = "0100") or (x = "0111") or (x = "1000") or (x = "1001")) else '0'; B(5) <= '1' when ((x = "0000") or (x = "0100") or (x = "0101") or (x = "0110") or (x = "1000") or (x = "1001")) else '0'; B(6) <= '1' when ((x = "0010") or (x = "0011") or (x = "0100") or (x = "0101") or (x = "0110") or (x = "1000") or (x = "1001")) else '0'; process(clock_in) begin if (rising_edge(clock_in)) then q_reg <= d_reg; end if; end process; process(latch_in) begin if (rising_edge(latch_in)) then x <= q_reg; end if; end process; end behavioral;
Tras compilar y sintetizar este código, la implementación eléctrica generada es la siguiente:
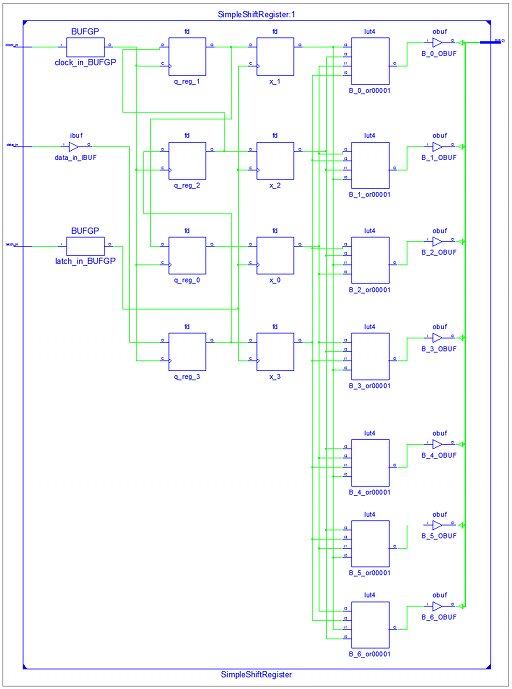
Como se puede ver, tanto el registro de desplazamiento como el latch se implementa mediante biestables D mientras que la lógica combinatoria de conversión de binario a 7 segmentos se implementa mediante LUTs (Look Up Tables), en lugar de mediante puertas lógicas. Esta forma de implementar lógica combinatoria es muy habitual en las FPGAs y los CPLDs.
Conexión con el Arduino
La FPGA funciona a 3.3 voltios mientras que el Arduino funciona a 5 voltios. Es necesario, por tanto adaptar los voltajes. En este caso concreto todas las señales salen del Arduino y entran en la FPGA por lo que se ha optado por hacer una adaptación de voltaje sencilla basada en transistores.
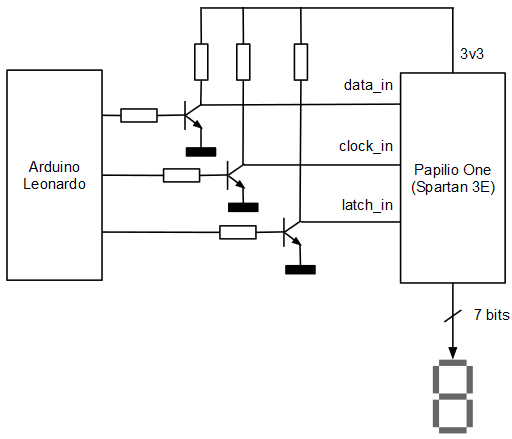
En el Arduino la función encargada de enviar un valor al display de 7 segmentos deberá colocar los datos de forma serie a través del pin data_in usando como reloj clock_in. Se activará latch_in cuando se desee mostrar en el display el valor cargado en el registro de desplazamiento. Obsérvese que al hacer la conversión de voltajes utilizando transistores NPN en configuración de emisor común, la lógica debe ser negada, es decir, para emitir un 1 de 3.3 voltios, emitimos un 0 de 5 voltios y para emitir un 0 de 3.3 voltios, emitimos un 1 de 5 voltios:
const int CLK_PIN = 0; const int DATA_PIN = 1; const int LATCH_PIN = 2; #define ONE LOW #define ZERO HIGH void byteOut(unsigned char v) { for (unsigned char i = 0; i < 4; i++) { if ((v & 1) != 0) digitalWrite(DATA_PIN, ONE); else digitalWrite(DATA_PIN, ZERO); delay(1); digitalWrite(CLK_PIN, ONE); delay(1); digitalWrite(CLK_PIN, ZERO); delay(1); v = v >> 1; } digitalWrite(LATCH_PIN, ONE); delay(1); digitalWrite(LATCH_PIN, ZERO); delay(1); }
A continuación puede verse un vídeo con el invento en funcionamiento:
Algunos enlaces para empezar con VHDL (en español)
Lista de reproducción de YouTube del profesor Carlos Fajardo sobre VHDL - Vídeos muy amenos y fáciles de seguir.
Libro online "Programación en VHDL" - Muy buen libro, aunque le echo en falta más ejemplos y ejercicios.
[ añadir comentario ] ( 2937 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 5191 )
( 3 / 5191 )La utilización de lógica borrosa o difusa (“fuzzy”) para el control de procesos permite abordar este tipo de problemas desde una perspectiva más "humana" ya que las reglas de la lógica borrosa son enunciados fácilmente comprensibles por una persona ajena a la teoría del control y su ajuste es más intuitivo que en el caso de controladores más "puros" como el PID. A lo largo de este post se abordará el control de velocidad de un sencillo motor DC mediante lógica borrosa utilizando sólo un puñado de reglas.
El problema
Se parte de un lazo de control estándar, el mismo que se utilizó cuando se implementó el control PID:
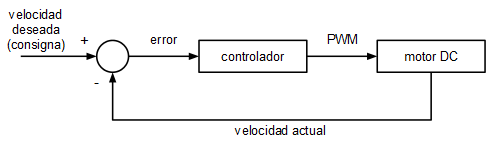
La velocidad se lee mediante un sencillo encoder compuesto por un disco pintado mitad de blanco y mitad de negro y por un sensor infrarrojo de tipo reflexivo (el CNY70, de los que suelen usarse en robots siguelineas).
El motor es accionado a través de una de las salidas PWM del microcontrolador mediante un transistor NPN de potencia.
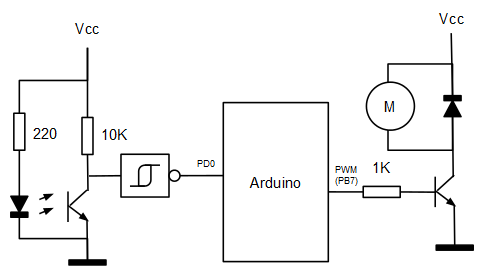
El esquema es exactamente el mismo que el utilizado en el post anterior.
Lectura de la velocidad angular
Para leer la velocidad angular se conecta la salida del sensor infrarrojo reflexivo (en concreto la salida del inversor schmitt) a una entrada de interrupción externa del microcontrolador y se programa dicha interrupción externa para que se dispare en uno de los flancos (subida o bajada, pero no en ambos a la vez). De esta forma y al estar el disco pintado mitad negro y mitad blanco, cada interrupción se corresponderá con una vuelta del eje de rotación.
float RPMReader::rpm; void RPMReader::init() { DDRD &= 0xFE; // PD0 as input cli(); EICRA = (1 << ISC01) | (1 << ISC00); // external INT0 EIMSK = (1 << INT0); sei(); Chronometer::init(); Chronometer::microseconds = 0; } void RPMReader::__isr() { uint32_t delta = Chronometer::microseconds; Chronometer::microseconds = 0; if (delta > 0) rpm = (((float) 1) / delta) * 60000000; EIFR |= (1 << INTF0); } ISR(INT0_vect) { RPMReader::__isr(); }
Cada vez que se ejecuta la interrupción (da una vuelta el eje de rotación) se obtiene la cantidad de microsegundos que han pasado desde la anterior vuelta y se calcula la velocidad angular:
uint32_t delta = Chronometer::microseconds; Chronometer::microseconds = 0; if (delta > 0) rpm = (((float) 1) / delta) * 60000000;
Señal PWM de salida
La salida del controlador borroso no es en este caso directamente el valor absoluto PWM, sino el "incremento" (o una especie de derivada) de dicho valor PWM. Esto simplifica el diseño del controlador borroso pero complica la etapa de salida, ya que hay que poner un "integrador" a la salida del controlador que convierta los incrementos PWM en valores absolutos PWM.

Afortunadamente este "integrador" no es más que un acumulador en el que se van sumando, en cada iteración, los incrementos que emite el controlador borroso. Es esta suma la que se emite como PWM para accionar el motor.
SpeedDeltaFuzzyValueWriter::SpeedDeltaFuzzyValueWriter() { this->sum = 0; } void SpeedDeltaFuzzyValueWriter::setValue(float v) { this->sum += v; if (this->sum > 255) this->sum = 255; else if (this->sum < 0) this->sum = 0; uint8_t aux = (uint8_t) this->sum; PWM::setPB7Value(aux); }
Control borroso
Para realizar el controlador se plantea como variable de entrada al mismo el error de la velocidad de rotación (deseada - actual) en revoluciones por minuto (RPM) y como variable de salida, el incremento (una especie de derivada) del ciclo de trabajo de la señal PWM que alimenta al motor DC. Se definen unos sencillos conjuntos borrosos asociados a cada una de estas dos variables:
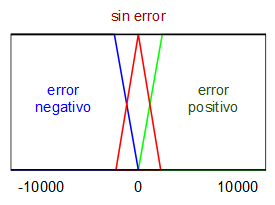
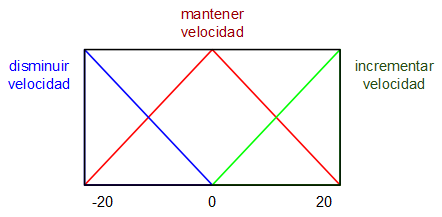
Mientras que las reglas de lógica borrosa que se van a utilizar son las siguientes:
SI (error ES error negativo) ENTONCES salida ES decrementar velocidad
SI (error ES sin error) ENTONCES salida ES mantener velocidad
SI (error ES error positivo) ENTONCES salida ES incrementar velocidad
Como puede apreciarse, las reglas son sencillas y fáciles de ajustar, de recordar y de mantener. Además, el hecho de que la variable de salida sea un incremento en lugar de un valor absoluto simplifica enormemente las reglas y los conjuntos.
Ejemplo 1
Supongamos que queremos alcanzar una velocidad de 3000 RPM y que la velocidad actual medida por el sensor de velocidad es de 2000 RPM, el error será, por tanto de 1000 RPM (consigna - valor real). Lo primero que se hace es “borrosificar” o “fuzzyficar” esta lectura:
Para la expresión “(error ES error negativo)” se calcula el grado de pertenencia de 1000 RPM al conjunto borroso “error negativo”, para la expresión “(error ES sin error)” se calcula el grado de pertenencia de 1000 RPM al conjunto borroso “sin error” y para la expresión “(error ES error positivo)” se calcula el grado de pertenencia de 1000 RPM al conjunto borroso “error positivo”:
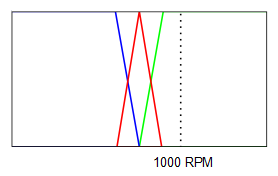
Como se puede ver:
$$\mu_{error \space negativo}(1000)=0$$
$$\mu_{sin \space error}(1000)=0$$
$$\mu_{error \space positivo}(1000)=1$$
Por lo tanto, para la salida:
$$\mu_{decrementar \space velocidad}(\Delta PWM)=0$$
$$\mu_{mantener \space velocidad}(\Delta PWM)=0$$
$$\mu_{incrementar \space velocidad}(\Delta PWM)=1$$
A continuación se calcula mediante el método de la media ponderada de centros, el valor de la salida:
$$\Delta PWM={0·C_{dec. \space velocidad}+0·C_{mant. \space velocidad}+1·C_{inc. \space velocidad} \over 0+0+1}=C_{inc. \space velocidad}=20$$
En este caso el resultado el directamente el centro del conjunto borroso “incrementar velocidad”, que vale 20, con lo que incrementamos la velocidad.
Ejemplo 2
Supongamos ahora que queremos alcanzar la misma velocidad de 3000 RPM y que la velocidad actual medida por el sensor de velocidad es de 3050 RPM, el error será, por tanto de -50 RPM (consigna - valor real). Lo primero que se hace de nuevo es “borrosificar” o “fuzzyficar” esta lectura:
Se calculan los diferentes grados de pertenencia:
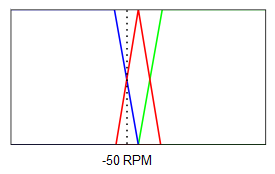
Como se puede ver:
$$\mu_{error \space negativo}(-50)=0.5$$
$$\mu_{sin \space error}(-50)=0.5$$
$$\mu_{error \space positivo}(-50)=0$$
Por lo tanto, para la salida:
$$\mu_{decrementar \space velocidad}(\Delta PWM)=0.5$$
$$\mu_{mantener \space velocidad}(\Delta PWM)=0.5$$
$$\mu_{incrementar \space velocidad}(\Delta PWM)=0$$
A continuación se calcula mediante el método de la media ponderada de centros, el valor de la salida:
$$\Delta PWM={0.5·C_{dec. \space velocidad}+0.5·C_{mant. \space velocidad}+0·C_{inc. \space velocidad} \over 0.5+0.5+0}=-10$$
Un valor de -10 en el incremento del PWM, disminuye dicho valor y, por tanto, hace que se disminuya la velocidad del motor.
En condiciones ideales, con una entrada de error de 0 RPM tendríamos:
$$\mu_{error \space negativo}(0)=0$$
$$\mu_{sin \space error}(0)=1$$
$$\mu_{error \space positivo}(0)=0$$
Por lo tanto, para la salida:
$$\mu_{decrementar \space velocidad}(\Delta PWM)=0$$
$$\mu_{mantener \space velocidad}(\Delta PWM)=1$$
$$\mu_{incrementar \space velocidad}(\Delta PWM)=0$$
Y haciendo la “desborrosificación” o “defuzzyficación” nos sale:
$$\Delta PWM={0·C_{dec. \space velocidad}+1·C_{mant. \space velocidad}+0·C_{inc. \space velocidad} \over 0+1+0}=C_{mant. \space velocidad}=0$$
Un incremento del valor PWM de 0, con lo que no cambiamos la velocidad del motor.
Para dotar al sistema de un comportamiento más estable, en los sistemas reales, suele tomarse también como entrada la derivada de la velocidad angular y establecer reglas que hagan variar el PWM en función de esta otra entrada. En este caso, por simplicidad, se ha optado por utilizar como entrada sólo la velocidad angular.
Implementación
La implementación se ha realizado en C++ y las clases definidas pueden dividirse en dos grupos: las que hacen de interfaz con hardware interno, entrada y salida (lectura del sensor de infrarrojos reflexivo para calcular la velocidad angular, salida PWM, timers, etc.) y las que forman parte del motor de inferencia borroso (expresiones, conjuntos borrosos, variables lingüísticas, reglas, etc.)
Diagrama de clases 1:
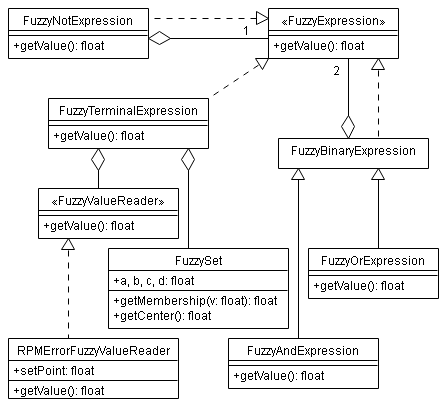
Diagrama de clases 2:
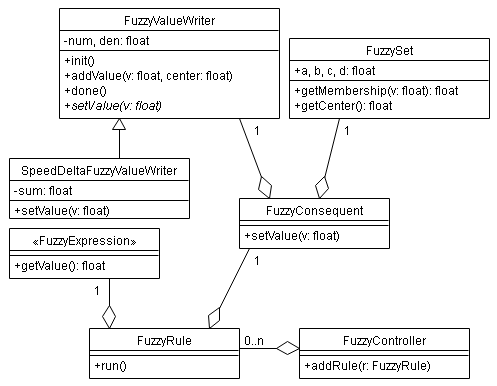
Los conjuntos borrosos (clase FuzzySet) se definen de forma trapezoidal:
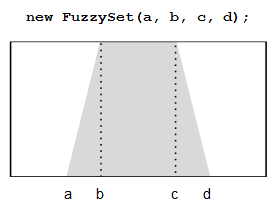
En el caso concreto que nos ocupa los conjuntos estarán, por tanto, definidos así:
FuzzySet negativeError(-10000, -10000, -100, 0); FuzzySet noError(-100, 0, 0, 100); FuzzySet positiveError(0, 100, 10000, 10000); FuzzySet decreaseSpeed(-20, -20, -20, 0); FuzzySet keepSpeed(-20, 0, 0, 20); FuzzySet increaseSpeed(0, 20, 20, 20);
Cada regla de inferencia borrosa estará definida por un antecedente (objeto de clase FuzzyExpression o derivadas) y por un consecuente (objeto de clase FuzzyConsequent).
FuzzyController c;
c.addRule(
new FuzzyTerminalExpression(entrada1, conjunto1),
new FuzzyConsequent(salida1, conjunto3)
); // SI (entrada1 ES conjunto1) ENTONCES salida1 ES conjunto3
En el antecedente podemos hacer combinaciones “Y”, “O” y “NO” utilizando las clases FuzzyAndExpression, FuzzyOrExpression y FuzzyNotExpression respectivamente.
c.addRule(
new FuzzyAndExpression(
new FuzzyTerminalExpression(entrada1, conjunto1),
new FuzzyTerminalExpression(entrada2, conjunto2)
),
new FuzzyConsequent(salida1, conjunto3)
); // SI (entrada1 ES conjunto1) Y (entrada2 ES conjunto2) ENTONCES salida1 ES conjunto3
De esta forma podemos crear reglas de inferencia borrosa tan complejas como queramos. Se ha aprovechado, además, la capacidad que tiene C++ de redefinir operadores y se han usado los operadores “&&”, “||”, “!” y “%” como sinónimos de FuzzyAndExpression, FuzzyOrExpression, FuzzyNotExpression y FuzzyTerminalExpression, respectivamente:
FuzzyExpression &avelino::operator % (FuzzyValueReader &vr, FuzzySet &fs) { FuzzyExpression *ret = FuzzyTerminalExpression::getInstance(vr, fs); return *ret; } FuzzyExpression &avelino::operator && (FuzzyExpression &e1, FuzzyExpression &e2) { FuzzyExpression *ret = FuzzyAndExpression::getInstance(e1, e2); return *ret; } FuzzyExpression &avelino::operator || (FuzzyExpression &e1, FuzzyExpression &e2) { FuzzyExpression *ret = FuzzyOrExpression::getInstance(e1, e2); return *ret; } FuzzyExpression &avelino::operator ! (FuzzyExpression &e) { FuzzyExpression *ret = FuzzyNotExpression::getInstance(e); return *ret; }
Ahora se puede escribir la regla de ejemplo de antes “SI (entrada1 ES conjunto1) Y (entrada2 ES conjunto2) ENTONCES salida 1 ES conjunto3” de la siguiente manera:
c.addRule(
(entrada1 % conjunto1) && (entrada2 % conjunto2),
new FuzzyConsequent(salida1, conjunto3)
);
Como se puede apreciar, la sintaxis se vuelve más clara y las reglas son más fáciles de leer y de mantener. En el caso que nos ocupa las reglas se definen de la siguiente manera:
c.addRule(
rpmError % negativeError,
new FuzzyConsequent(speedDelta, decreaseSpeed)
);
c.addRule(
rpmError % noError,
new FuzzyConsequent(speedDelta, keepSpeed)
);
c.addRule(
rpmError % positiveError,
new FuzzyConsequent(speedDelta, increaseSpeed)
);
Finalmente, en el bucle principal de la aplicación lo único que se hace es iterar el motor de inferencia borroso (FuzzyController::run) cada 200 milisegundos:
DDRC |= 0x80; while (true) { if (Chronometer::microseconds2 > 200000) { // each 200ms Chronometer::microseconds2 = 0; c.run(); } // turn on led when set point reached if ((RPMReader::rpm >= SET_POINT_LOW) && (RPMReader::rpm <= SET_POINT_HIGH)) PORTC |= 0x80; else PORTC &= 0x7F; }

Todo el código fuente puede descargarse de la sección soft.
[ 2 comentarios ] ( 12576 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 6196 )
( 3 / 6196 )Uno de los controladores más utilizados es el tipo PID (Proporcional Integral Derivativo). A lo largo de este post se abordará la implementación de uno en Arduino para controlar la velocidad de un motor DC.
Un poco de teoría
Cuando se quiere controlar una planta (en nuestro caso un motor DC), lo más habitual es plantear un lazo de control estándar:
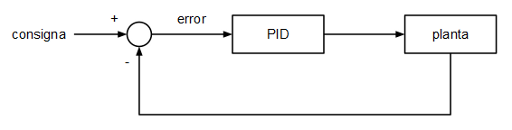
La señal que entra al controlador es la medida que queremos que alcance la planta (llamada "consigna" en teoría del control) menos la medida de salida de la planta o, lo que es lo mismo, el error. El objetivo del controlador será siempre minimizar el valor absoluto del error (que tienda a cero) actuando sobre la entrada de la planta.
Para profundizar bien en el estudio del control habría que ver las transformadas de Laplace, los polos y los ceros del sistema y, para el caso discreto, lo ideal sería un estudio basado en la transformada Z estudiando también la ubicación de los polos y los ceros. Sin embargo me centraré en el estudio y la implementación de un controlador estándar: el PID.
PID
Los controladores PID son un tipo especial de controlador que combinan la acción proporcional (P), la acción integral (I) y la acción derivativa (D) sobre el error. Si a la entrada del controlador (el error) la llamamos e(t) y a la salida del controlador (la entrada a la planta, en nuestro caso la entrada al motor DC) la llamamos u(t). Podemos definir un PID de la siguiente manera:
$$u(t)=K_pe(t)+K_i\int_0^t e(\tau)d\tau+K_d{de(t) \over dt}$$
Como se puede apreciar, la acción proporcional vendrá determinada por la constante $K_p$, la acción integral por la constante $K_i$ y la acción derivativa por la constante $K_d$.
1. La acción proporcional $K_p$ hace que el error en estado estacionario tienda a cero.
2. La acción integral $K_i$, al ir sumando los errores en el tiempo (integral), tiende a eliminar el error estacionario generado por la acción proporcional.
3. La acción derivativa $K_d$ tiende a suavizar las variaciones en el error.
Para determinar los mejores valores de cada una de las constantes, lo ideal es realizar un estudio mediante la transformada de Laplace y buscar la mejor ubicación de los polos y los ceros del controlador PID para que se obtenga el comportamiento deseado.
En este caso se ha optado por realizar pruebas empíricas con valores bajos e ir probando diferentes combinaciones.
Implementación a nivel hardware
En este caso la planta es un motor DC del que vamos a controlar su velocidad mediante la salida PWM de 8 bits (0 a 255) y 5 voltios. La salida PWM la conectamos a la base de un transistor NPN de potencia (en este caso un BD139) montado en configuración de emisor común.
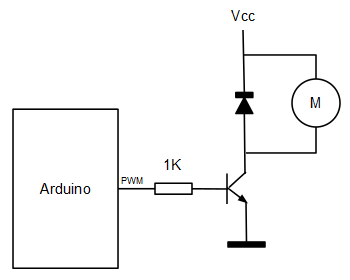
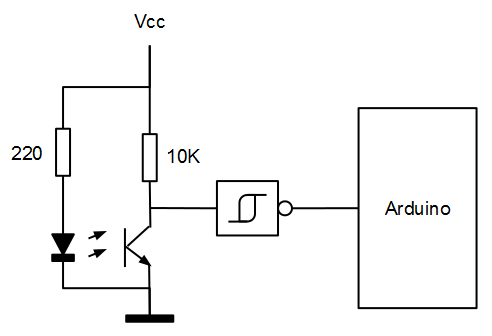
La lectura de la velocidad angular la hacemos utilizando un disco pintado (mitad blanco y mitad negro) conectado al eje de rotación (para que gire) y un sensor reflexivo de infrarrojos CNY70 (del que se utiliza en los robots sigue líneas).

Polarizando el fototransistor y el led infrarrojo y acondicionando la señal con una puerta inversora de tipo schmitt, ya tenemos un flanco de subida o de bajada por cada vuelta que da el disco.
Implementación a nivel software
Lectura de la velocidad
Para obtener la velocidad de rotación lo más eficiente es conectar la salida del inversor schmitt a una entrada del microcontrolador que permita disparar interrupciones internas en cada flanco de bajada o en cada flanco de subida. El pseudocódigo sería como sigue:
rpm = 0
anterior_t = 0
cada vez que haya un flanco de subida hacer:
t = microsegundos
incremento = t - anterior_t
rpm = (1 / incremento) * 60000000
anterior_t = t
fin interrupción
De esta forma tenemos los rpm a los que va el motor. Nótese que esta implementación no detecta la velocidad de 0 rpm. Para detectar la velocidad de 0 rpm habría que incluir un timer que, pasado un tiempo determinado, si no se produce la interrupción, asuma que el disco se ha parado (rpm = 0). En este caso no se ha implementado esta funcionalidad por simplicidad.
Implementación del PID
Para implementar el controlador PID en el Arduino (o en cualquier otro microcontrolador) tenemos que discretizar la ecuación diferencial que relaciona u(t) con e(t). Separamos primero dicha ecuación diferencial en partes:
$$u(t)=u_p(t)+u_i(t)+u_d(t)$$
Siendo:
$$u_p(t)=K_pe(t)$$
$$u_i(t)=K_i\int_0^t e(\tau)d\tau$$
$$u_d(t)=K_d{de(t) \over dt}$$
La discretización de $u_p(t)$ es trivial:
$$u_p[k]=K_pe[k]$$
La discretización de $u_i(t)$ asumiento un período de muestreo de $T$ lo suficientemente bajo la podemos calcular aproximando la integral mediante una suma de áreas de rectángulos de base $T$ y altura $e[k]$:
$$u_i[k]=K_i\sum_{n=0}^kTe[n]=K_iT\sum_{n=0}^ke[n]$$
De la misma manera, la discretización de $u_d(t)$ asumiento un período de muestreo $T$ lo suficientemente bajo la podemos calcular aproximando la derivada mediante el cálculo de la pendiente de la recta que une $e[k-1]$ con $e[k]$:
$$u_d[k]=K_d{e[k]-e[k-1] \over T}$$
El PID discretizado nos quedaría, por tanto, de la siguiente manera:
$$u[k]=K_pe[k]+K_iT\sum_{n=0}^ke[n]+K_d{e[k]-e[k-1] \over T}$$
Esta ecuación en diferencias finitas sí es fácilmente implementable en cualquier sistema. En el caso de Arduino podríamos realizar la siguiente implementación:
struct pid_controller { float kp, ki, kd; float delta; float sum; float prevError; }; void pid_controller_init(struct pid_controller &pid, float delta, float kp, float ki, float kd) { pid.delta = delta; pid.kp = kp; pid.ki = ki; pid.kd = kd; pid.sum = 0; pid.prevError = 0; } float pid_controller_run(struct pid_controller &pid, float error) { float p = pid.kp * error; pid.sum += error; float i = pid.ki * pid.delta * pid.sum; float d = pid.kd * (error - pid.prevError) / pid.delta; pid.prevError = error; return p + i + d; }
Las pruebas empíricas realizadas han dado muy buenos resultados para:
$$K_p=K_i=K_d=0.5$$
Con un período de muestreo $T=0.01$. La inicialización, por tanto, quedaría así:
void setup() { ... pid_controller_init(motor_pid_controller, 0.01, 0.5, 0.5, 0.5); ... }
Mientras que cada 10 milisegundos ($T=0.01$) habrá que calcular el PID:
const float SET_POINT = 1600; // consigna en rpm unsigned long last_t = 0; void loop() { unsigned long t = millis(); if ((t - last_t) >= 10) { float error = SET_POINT - current_rpm; float u = pid_controller_run(motor_pid_controller, error); analogWrite(PWM_OUTPUT, (int) u); last_t = t; } }
Pruebas realizadas
Para una consigna de 1000 rpm, la velocidad angular medida utilizando el PID es la siguiente (100ms entre medida y medida):
1013.99 rpm
1025.57 rpm
1013.03 rpm
1019.02 rpm
986.13 rpm
1003.95 rpm
1002.00 rpm
1013.65 rpm
999.07 rpm
977.64 rpm
1013.99 rpm
1037.49 rpm
1018.26 rpm
998.14 rpm
986.71 rpm
1006.64 rpm
1017.29 rpm
1017.43 rpm
Mientras que para una consigna de 1600 rpm, la velocidad angular medida fue la siguiente (100ms entre medida y medida):
1632.03 rpm
1591.01 rpm
1602.56 rpm
1583.28 rpm
1608.92 rpm
1578.28 rpm
1599.66 rpm
1583.61 rpm
1586.29 rpm
1616.21 rpm
1619.35 rpm
1594.39 rpm
1601.54 rpm
1581.11 rpm
1601.37 rpm
1606.68 rpm
1570.52 rpm
1602.39 rpm
El código fuente para Arduino puede descargarse de la sección soft.

[ añadir comentario ] ( 4642 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 6317 )
( 3 / 6317 )Cuando pensamos en detectar determinadas frecuencias o tonos en una señal lo primero que se nos viene a la cabeza suele ser la FFT, en concreto la implementación de Cooley-Tukey con N potencia de 2. La FFT está muy bien si lo que queremos es todo el espectro de una señal, pero si lo que necesitamos es detectar un único tono en una frecuencia concreta podemos recurrir al algoritmo de Goertzel, más rápido y muy fácil de implementar en sistemas embebidos.
El algoritmo de Goertzel permite calcular un coeficiente aislado de la DFT sobre un conjunto de N muestras con una complejidad temporal de O(n) y una complejidad espacial de O(1), además N no tiene por qué ser potencia de 2. Este algoritmo se basa en la aplicación de una ecuación en diferencias finitas (un filtro IIR).
A mayor N, mayor resolución en frecuencia y también mayor latencia en la detección de los tonos. Es necesario, por tanto encontrar un compromiso. La resolución en hercios del algoritmo de Goertzel viene dada por:
$$R = {f_s \over N}$$
Siendo $f_s$ la frecuencia de muestreo y $N$ el número de muestras que se evalúan en cada pasada.
1. Se calcula el índice del coeficiente correspondiente
Lo primero que hay que hacer es calcular el índice del coeficiente asociado a la DFT a partir de la frecuencia que queremos detectar:
$$k = N{f \over f_s}$$
Siendo $f$ la frecuencia que queremos detectar, $f_s$ la frecuencia de muestreo y $N$ el número de muestras que procesamos cada vez. La máxima frecuencia que podemos detectar será la mitad de la frecuencia de muestreo.
2. Para cada conjunto de N muestras
2.1. Se aplica la ecuación en diferencias
Para cada una de las muestras que van llegando, vamos aplicando la siguiente ecuación en diferencias finitas:
$$s[n] = x[n] + 2\cos\left({2 \pi k \over N}\right)s[n-1] - s[n-2]$$
$$n = 0..N$$
Con codiciones iniciales $s[-1] = s[-2] = 0$. Se trata, como se puede ver, de un sencillo filtro IIR de segundo orden.
2.2. Se obtiene del coeficiente k-esimo de la DFT
Se puede demostrar que el coeficiente k-ésimo de la DFT de tamaño N es:
$$X(k) = s[N] - W_N^ks[N-1]$$
Siendo:
$$W_N = e^{-j\left({2 \pi \over N}\right)}$$
Por tanto:
$$X(k) = s[N] - e^{-j\left({2 \pi \over N}\right)k}s[N-1]$$
Si desarrollamos la exponencial compleja mediante la fórmula de Euler tenemos que:
$$e^{-j\left({2 \pi \over N}\right)k} = \cos\left({2 \pi \over N}\right) - j \sin\left({2 \pi k \over N}\right)$$
Y, por tanto:
$$X(k)_{real} = s[N] - \cos\left({2 \pi k \over N}\right)s[N-1]$$
$$X(k)_{imag} = \sin\left({2 \pi k \over N}\right)s[N-1]$$
Para calcular la magnitud de la banda de frecuencia correspondiente calculamos el módulo de $X(k)$:
$$M^2 = \left|X(k)\right|^2 = X(k)_{real}^2 + X(k)_{imag}^2$$
De esta forma podemos medir la magnitud de la banda de frecuencia correspondiente al coeficiente k-ésimo de la DFT o, lo que es lo mismo, la magnitud de la banda de frecuencia correspondiente a la frecuencia $f$.
$$k = N{f \over f_s} \Rightarrow f = {k f_s \over N}$$
Implementación
A continuación se puede ver una implementación del algoritmo de Goertzel en Arduino:
const int ANALOG_INPUT = A0; const int SAMPLE_RATE_HZ = 3000; const int SAMPLE_PERIOD_US = 1000000 / SAMPLE_RATE_HZ; const int F_HZ = 440; const int N = 3000; const int K = 440; // N * F_HZ / SAMPLE_RATE_HZ; unsigned long tPrev; struct goertzelFilter { float s1, s2; int k, n; float sinv, cosv, cosv2; int nextIteration; }; struct goertzelFilter filter; void goertzelFilterReset(struct goertzelFilter &f) { f.s1 = 0; f.s2 = 0; f.nextIteration = 0; } void goertzelFilterInit(struct goertzelFilter &f, int k, int n) { f.k = k; f.n = n; f.cosv = cos(2 * PI * k / n); f.sinv = sin(2 * PI * k / n); f.cosv2 = 2 * f.cosv; goertzelFilterReset(f); } boolean goertzelFilterFinished(struct goertzelFilter &f) { return (f.nextIteration == (f.n + 1)); } void goertzelFilterRun(struct goertzelFilter &f, float input) { float s = input + (f.cosv2 * f.s1) - f.s2; f.s2 = f.s1; f.s1 = s; f.nextIteration++; } float goertzelFilterGetMagnitude(struct goertzelFilter &f) { float real = f.s1 - (f.cosv * f.s2); float imag = f.sinv * f.s2; return ((real * real) + (imag * imag)); } void setup() { Serial.begin(9600); tPrev = micros(); goertzelFilterInit(filter, K, N); goertzelFilterReset(filter); } void loop() { unsigned long t = micros(); if ((t - tPrev) >= SAMPLE_PERIOD_US) { int v = analogRead(ANALOG_INPUT); if (goertzelFilterFinished(filter)) { float magnitude = goertzelFilterGetMagnitude(filter); Serial.println(magnitude); goertzelFilterReset(filter); } else goertzelFilterRun(filter, ((float) v - 512) / 512); tPrev = t; } }
Se ha elegido una frecuencia de muestreo baja (3000Hz) para poder trabajar cómodamente con tipos float. Utilizando aritmética de punto fijo podríamos incremenentar la frecuencia de muestreo y que la detección sea más precisa.
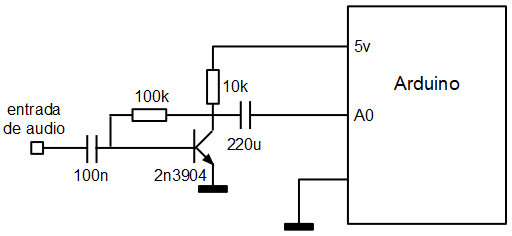
La entrada de audio se toma de la entrada analógica A0 a la que se conecta un sencillo circuito amplificador:
Elegir el valor de N
A la hora de elegir la N lo ideal es escogerla lo más grande posible, que nos permita una latencia razonable y que se cumpla que:
$$k = N{f \over f_s} \in \mathbb{N}$$
Por ejemplo, para detectar un tono de 1Khz sobre una señal muestreada a 6KHz lo ideal sería que la N valiese: 96, 102, 114… Ya que para todos estos valores se cumple que $k$ es número natural.
Magnitudes medidas para diferentes tonos
En ausencia de señal de entrada: 0.30, 0.37, 0.30, 0.35, 0.44, 0.32, 0.37, 0.28...
Con una señal de entrada de 200Hz: 2.56, 1.73, 3.56, 0.81, 0.58, 1.67, 4.71, 6.81...
Con una señal de entrada de 440Hz (la frecuencia del detector): 138.41, 87.29, 441.14, 185.20, 233.03, 762.27, 80.62, 330.98...
Con una señal de entrada de 500Hz: 25.70, 9.60, 22.50, 2.76, 16.62, 18.75, 23.56, 35.58...

[ añadir comentario ] ( 3703 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 5408 )
( 3 / 5408 )Los perceptrones multicapa (Multilayer Perceptron o MLP) son redes neuronales de aprendizaje supervisado de tipo unidireccional en las que tenemos una capa de neuronas de entrada, una o más capas de neuronas intermedias y una capa de neuronas de salida. Son muy utilizadas para reconocimiento y clasificación de patrones y relativamente sencillas de implementar en sistemas embebidos utilizando aritmética de punto fijo.
En un MLP cada neurona tiene una salida y n entradas y se modela de la siguiente manera:
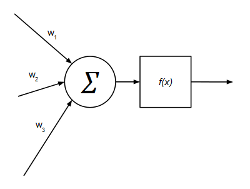
Las entradas de cada neurona suman de forma ponderada (pesos sinápticos) y dicha suma ponderada se hace pasar por una función de activación que, en el caso más general (clasificadores), se trata de la función sigmoide:
$$f(x) = {{1} \over {1+e^{-x}}}$$
Los MLP son estructuras de neuronas organizadas en forma de capas:
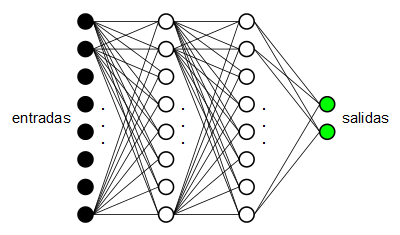
En este caso tenemos un MLP con 8 neuronas de entrada (las neuronas de entrada no son neuronas en sí, se les llama neuronas pero realmente son simplemente las entradas de la red), dos capas (denominadas “ocultas”) de 8 neuronas cada una y una capa de salida de 2 neuronas.
Los MLP con función de activación sigmoide son más utilizados para reconocimiento y clasificación de patrones. En este caso se abordará este tipo de MLP utilizando el clásico algoritmo de aprendizaje Backpropagation.
Algoritmo Backpropagation
El algoritmo Backpropagation consiste en hacer pasar por la red una serie de patrones predefinidos para los que se indica una salida “esperada”. La salida real que emite la red para cada uno de los patrones de entrada se compara con la salida “esperada” y se recalculan los pesos sinápticos hacia atrás (desde la salida hasta la entrada). De ahí el nombre del algoritmo. Los pasos de dicho algoritmo son los siguientes:
Evaluar la red
Se evalúa la red, esto es, para cada neurona desde la capa de entrada hasta la capa de salida se realiza el cálculo de los valores de salida de cada neurona utilizando la ecuación:
$$suma^{o}_{pk} = \sum_{j=1}^{L}w_{kj}^{o}y_{pj} + \theta_{k}^{o}$$
$$y_{pk}=f_{k}^{o}(suma^{o}_{pk})$$
Siendo:
$w_{kj}^{o}$ el peso sináptico de la neurona $j$ de la capa anterior sobre la neurona $k$ de la capa actual.
$f$ la función de activación (en este caso la sigmoide).
Calcular los términos del error
Para cada neurona $k$ de la capa de salida se calcula su error:
$$\delta_{pk}^{o}=(d_{pk}-y_{pk})f_{k}^{'o}(suma_{pk}^{o})$$
Siendo:
$d_{pk}$ el valor deseado para la neurona $k$ de la capa salida y para el patrón de entrada $p$.
$y_{pk}$ el valor actual de la neurona $k$ de la capa de salida para el patrón $p$.
$f'$ la derivada de la función de activación (derivada de la función sigmoide).
Mientras que para cada neurona $j$ de cada capa oculta $h$ el error hay que estimarlo a partir de los errores de la capa siguiente:
$$\delta_{pj}^{h}=f_{j}^{'h}(suma_{pj}^{h})\sum_{k}\delta_{pk}^{o}w_{kj}^{o}$$
Siendo:
$p$ el vector de entrenamiento.
$suma_{pj}^{h}$ la entrada neta (suma ponderada) de la neurona $j$ en la capa $h$ para el vector $p$.
$\delta_{pk}^{o}$ el término de error de la neurona $k$ de la capa anterior.
$w_{kj}^{o}$ el peso de la salida de la neurona $j$ de la capa anterior sobre la neurona $k$.
Actualizar los pesos
$$w_{kj}^{o}(t+1)=w_{kj}^{o}(t)+\Delta w_{kj}^{o}(t+1)$$
$$\Delta w_{kj}^{o}(t+1)=\alpha \delta_{pk}^{o}y_{pj}$$
Siendo:
$w_{kj}^{o}$ el peso de la salida de la neurona $j$ de la capa anterior sobre la neurona $k$.
$y_{pj}$ la salida de la neurona $j$ (la del extremo origen del peso $w_{kj}^{o}$).
Se repite hasta que el error sea aceptable
$$E_{p}={1 \over 2}\sum_{k}\delta_{pk}^{2}$$
Siendo:
$\delta_{pk}$ el error de la neurona $k$ de la capa de salida para el patrón de entrada $p$.
Implementación en punto fijo
En el caso de que queramos implementar una red neuronal de tipo MLP en un sistema embebido sin unidad de coma flotante, debemos intentar realizar una implementación en punto fijo de toda la operativa (tanto evaluación como aprendizaje de la red). Como se puede ver en la ecuaciones mostradas, la parte más compleja viene dada por la función de activación.
$$f(x)={1 \over {1+e^{-x}}}$$
Y por su derivada:
$$f'(x)={{e^{-x}} \over {(1+e^{-x})^2}}$$
Utilizando aproximantes de Padé de orden [3 / 3] para el cálculo de la exponencial podemos aproximar ambas funciones de forma razonablemente buena.
$$e^{x} \simeq {{1+{x \over 2}+{{x^2} \over 10}+{{x^3} \over 120}} \over {1-{x \over 2}+{{x^2} \over 10}-{{x^3} \over 120}}}$$
fixedpoint_t FixedPoint::getExp(fixedpoint_t x) { fixedpoint_t x2 = FP_MUL(x, x); fixedpoint_t x3 = FP_MUL(x2, x); fixedpoint_t num = TO_FP(1) + FP_DIV(x, TO_FP(2)) + FP_DIV(x2, TO_FP(10)) + FP_DIV(x3, TO_FP(120)); fixedpoint_t den = TO_FP(1) - FP_DIV(x, TO_FP(2)) + FP_DIV(x2, TO_FP(10)) - FP_DIV(x3, TO_FP(120)); return FP_DIV(num, den); } [...] fixedpoint_t MultilayerPerceptron::getNetValue(uint8_t numNeuronsPrevLayer, uint8_t currentLayer, uint8_t n) { fixedpoint_t acc = 0; for (uint8_t p = 0; p < numNeuronsPrevLayer; p++) { fixedpoint_t x = this->getNeuronValue(currentLayer - 1, p); fixedpoint_t w = this->getInputWeight(currentLayer, p, n); acc = acc + FP_MUL(x, w); } return acc; } fixedpoint_t MultilayerPerceptron::getSigmoid(fixedpoint_t x) { return FP_DIV(TO_FP(1), TO_FP(1) + FixedPoint::getExp(-x)); } void MultilayerPerceptron::evaluate() { uint8_t numLayers = this->getNumHiddenLayers() + 1; for (uint8_t l = 1; l <= numLayers; l++) { uint8_t numNeurons = this->getNumNeurons(l); uint8_t numNeuronsPrevLayer = this->getNumNeurons(l - 1); for (uint8_t n = 0; n < numNeurons; n++) { fixedpoint_t acc = this->getNetValue(numNeuronsPrevLayer, l, n); fixedpoint_t y = MultilayerPerceptron::getSigmoid(acc); this->setNeuronValue(l, n, y); } } }
Para el algoritmo de entrenamiento Backpropagation es necesario utilizar la derivada de la función de activación. Esta derivada puede simplificarse y ponerse en función de la propia función sigmoide:
$$f'(x)={{e^{-x}} \over {(1+e^{-x})^2}}={1 \over {1+e^{-x}}}{{e^{-x}} \over {1+e^{-x}}}=f(x){{e^{-x}} \over {1+e^{-x}}}$$
$$f'(x)=f(x){{1+e^{-x}-1} \over {1+e^{-x}}}=f(x)\left({{1+e^{-x}} \over {1+e^{-x}}}-{1 \over {1+e^{-x}}}\right)$$
$$f'(x)=f(x)\left(1-{1 \over {1+e^{-x}}}\right)=f(x)(1-f(x))$$
Por tanto, para la función sigmoide, se cumple que:
$$f'(x)=f(x)(1-f(x))$$
Como $f(x)$ se corresponde con la salida de cada neurona (siendo $x$ la suma ponderada de sus entradas), la derivada de la salida de cada neurona puede calcularse, por tanto, de esta manera:
$$salida(1-salida)$$
En el algoritmo de entrenamiento Backpropagation esto simplifica enormemente el cálculo de los términos de error ya que se puede calcular la derivada de cada neurona a partir de su valor de salida.
fixedpoint_t MultilayerPerceptron::getEstimatedError(uint8_t layer, uint8_t n) { uint8_t numLayers = this->getNumHiddenLayers() + 1; fixedpoint_t ret = 0; if (layer == numLayers) { fixedpoint_t out = this->getNeuronValue(layer, n); ret = (this->getDesiredOutput(n) - out); } else { uint8_t numNeuronsNextLayer = this->getNumNeurons(layer + 1); for (uint8_t k = 0; k < numNeuronsNextLayer; k++) { fixedpoint_t e = this->getNeuronErrorValue(layer + 1, k); fixedpoint_t w = this->getInputWeight(layer + 1, n, k); ret += FP_MUL(e, w); } } return ret; } void MultilayerPerceptron::backpropagate(uint8_t layer, fixedpoint_t *totalError) { if (totalError != NULL) *totalError = 0; uint8_t numNeurons = this->getNumNeurons(layer); for (uint8_t n = 0; n < numNeurons; n++) { fixedpoint_t out = this->getNeuronValue(layer, n); fixedpoint_t aux = FP_MUL(out, TO_FP(1) - out); // derivada de la función de activación fixedpoint_t error = FP_MUL(aux, this->getEstimatedError(layer, n)); this->setNeuronErrorValue(layer, n, error); if (totalError != NULL) *totalError += FP_MUL(error, error); } uint8_t numNeuronsPrevLayer = this->getNumNeurons(layer - 1); for (uint8_t n = 0; n < numNeurons; n++) { fixedpoint_t e = this->getNeuronErrorValue(layer, n); for (uint8_t k = 0; k < numNeuronsPrevLayer; k++) { fixedpoint_t y = this->getNeuronValue(layer - 1, k); fixedpoint_t w = this->getInputWeight(layer, k, n); w = w + FP_MUL(this->trainRate, FP_MUL(e, y)); this->setInputWeight(layer, k, n, w); } } } void MultilayerPerceptron::train(uint8_t times, fixedpoint_t &totalError) { while (times > 0) { uint8_t outputLayer = this->getNumHiddenLayers() + 1; for (uint8_t l = outputLayer; l >= 1; l--) { fixedpoint_t *e = (l == outputLayer) ? &totalError : NULL; this->backpropagate(l, e); } this->commitInputWeights(); times--; } }
Se ha utilizado como tipo funto fijo el formato Q16.16 mapeado sobre un entero de 32 bits (int32_t), esto nos da una precisión de
$$2^{-16} = 0,0000152587890625$$
Un error bastante aceptable teniendo en cuenta lo que vamos a ganar en velocidad.
typedef int32_t fixedpoint_t; #define FP_FRACTIONAL_BITS 16 #define FP_MUL(x, y) ((((int64_t) (x)) * ((int64_t) (y))) >> 16) #define FP_DIV(x, y) ((((int64_t) (x)) << 16) / ((int64_t) (y))) #define TO_FP(x) (((int32_t ) (x)) << 16)
Pruebas realizadas
Las pruebas se han realizado partiendo de dos patrones de entrenamiento sencillos:
$p_{1}=\{0, 0, 0, 0, 0, 1, 1, 1\}$ que debe generar la salida $\{0, 1\}$.
$p_{2}=\{0, 1, 1, 0, 0, 0, 0, 1\}$ que debe generar la salida $\{1, 0\}$.
Con los que se han obtenido muy buenos resultados:
Para el patrón $p_{1}$ se obtiene, tras el entrenamiento, la salida $$\{0.0270996, 0.972183\}$$
Para el patrón $p_{2}$ se obtiene, tras el entrenamiento, la salida $$\{0.971191, 0.0284729\}$$
Todo el código fuente puede descargarse de la sección soft.
[ añadir comentario ] ( 2688 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 5605 )
( 3 / 5605 )
 Calendario
Calendario




