Un receptor de radio superheterodino es un receptor de radio que realiza un proceso de mezcla de frecuencias para convertir la señal de la antena a una frecuencia fija fácilmente procesable por los circuitos de demodulación, siendo la gran mayoría de los receptores de radio actuales de este tipo. En este pequeño proyecto se aborda la implementación de un receptor de radio superheterodino pero implementando la mayor parte del proceso directamente en circuitos digitales dentro de una FPGA.

Heterodinización

El proceso de heterodinización consiste en trasladar la frecuencia de una emisora que queremos sintonizar a otra frecuencia que es más cómoda a nivel electrónico o de procesamiento, para demodular. Este proceso se consigue en circuitería analógica normalmente mediante lo que se denomina un mezclador (multiplicador) en combinación con un oscilador: Si multiplicamos la señal que llega de una antena por una señal sinusoidal de un oscilador local conseguimos realizar un desplazamiento de todas las frecuencias que llegan a la antena de tal manera que si tenemos una emisora en $f_1$ y nuestro oscilador local genera una señal en $f_2$, el resultado serán dos señales con las mismas características que $f_1$ pero desplazadas en frecuencia: una en $f_1 + f_2$ y otra en $f_1 - f_2$.

Si denominamos a $f_1 - f_2 = f_i$ frecuencia intermedia podemos dejar pasar sólo dicha frecuencia mediante un filtro paso-banda (con la ventaja añadida de que dicho filtro es de frecuencia fija) y realizar todo el proceso de demodulación basándonos sólo en esta frecuencia intermedia, independientemente de a qué frecuencia esté emitiendo la emisora (independientemente de $f_1$) puesto que con el mezclador y el oscilador local ya desplazamos la señal de la emisora como si emitiese en $f_i$. En los receptores superheterodinos lo que se hace normalmente es elegir una frecuencia $f_i$ relativamente cómoda (el estándar es 455 KHz para AM y 10.7 MHz para FM). De esta manera, por ejemplo, para un receptor AM comercial que deba recibir emisoras en la banda entre 530 y 1710 KHz, su oscilador local generará frecuencias en el rango de 985 a 2165 KHz; así, para recibir una emisora que emita a 576 KHz, el receptor generará una señal en su oscilador local de 1031 KHz que, al ser multiplicada por la señal de antena, proporcionará un par de frecuencias resultado de esa multiplicación estando una de dichas frecuencias en 455 KHz. Y así con cualquier emisora: basta con alterar la frecuencia del oscilador local para cambiar de emisora, el resto de la circuitería del receptor trabaja a 455 KHz.

Implementación en digital

Como objetivo inicial nos planteamos un receptor sencillo AM para la banda comercial, puesto que la demodulación en amplitud suele ser un proceso más sencillo que la demodulación en frecuencia (FM). Como se vio anteriormente el proceso de heterodinización consiste básicamente en multiplicar la señal de antena por otra señal procedente de un oscilador local. El primer escollo que nos encontramos es la lectura de la señal de la antena y su posterior conversión analógico-digital.

Amplificador analógico para la antena

El amplificador analógico de antena hace una amplificación de banda ancha (no sintonizada) pero necesaria para que el ADC pueda detectar señal. He utilizado una configuración estándar de amplificador en emisor común.



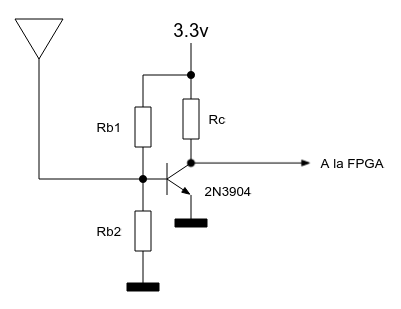
En las pruebas con el prototipo se optó por ajustar las dos resistencias de la base de forma empírica con un potenciómetro ajustable de 10 K en modo divisor de tensión hasta que la calidad fuera la mejor posible. Al usarse un transistor 2N3904 la resistencia del colector sí se calculó utilizando las curvas características:



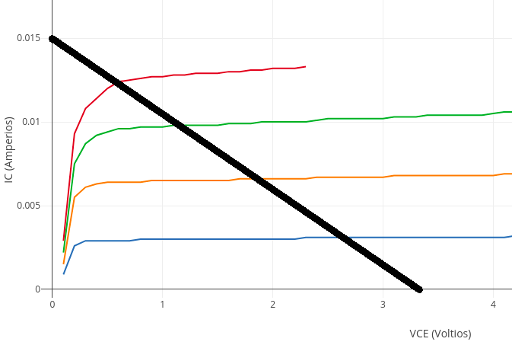
Usamos el valor de $220 \Omega$ para $R_c$ puesto que con ese valor tenemos una recta de carga con mínima distorsión y ganancia razonable, que toca, en el eje X, al punto $V_{cc} = 3.3 V$ y, en el eje Y, al punto ${3.3 \over 220} = 0.015 A$.

ADC para la entrada de la antena

Tratamos de usar una conversión "barata" de tipo delta-sigma, de la que hablamos en una entrada anterior, usando un comparador LVDS interno de la FPGA (todas las FPGA vienen con entradas diferenciales incorporadas basadas en comparadores LVDS). Este tipo de conversión es muy eficiente, permite resolución arbitraria pero, a cambio, requiere mucho sobremuestreo (oversampling) para obtener lecturas fiables. Al tener nuestra FPGA un reloj a 50 MHz, el sobremuestreo nos puede resultar muy caro a efectos de ancho de banda: por ejemplo para obtener una resolución de 8 bits en el ADC ya no podríamos muestrear a 50 MHz, sino a ${50000000 \over {2^8}} = 195 \: KHz$ con lo cual el ancho de banda del ADC caería a los 97 KHz y ya nos iríamos fuera del rango de la banda AM que queríamos abarcar inicialmente.

¿Qué pasa si, manteniendo la frecuencia de reloj de 50 MHz, subimos la frecuencia de muestreo a costa de una pérdida de resolución en el ADC? Más aún ¿Qué pasa si nos vamos al caso extremo de poner la frecuencia de muestreo a 50 MHz y de considerar un ADC de 1 bit de resolución? Bueno, uno puede pensar, a priori que esa pérdida en los bits de resolución es inasumible, pero lo cierto es que, si el ADC es de tipo delta-sigma, aunque la resolución del ADC sea de 1 bit, la anchura de los pulsos será proporcional al nivel de la entrada y, a nivel espectral, la señal de entrada seguirá siendo fiel reflejo de lo que llega por la antena, al menos hasta cierta frecuencia. Bueno, probemos entonces con un ADC de 1 bit a ver qué tal.

Elección de la frecuencia intermedia

Como se vio al principio, en los circuitos electrónicos, lo usual es elegir frecuencias intermedias que sean cómodas de cara al cálculo de componentes, de cara a la minimización del ruido, precio, rendimiento, etc. Sin embargo si estamos realizando el mezclado (la multiplicación) de las señales y la posterior demodulación dentro de una FPGA, la elección de la frecuencia intermedia (los 455 KHz que elegimos para el receptor AM) se convierte en una elección totalmente arbitraria: podríamos elegir la frecuencia que quisiéramos. En el caso que nos ocupa, y siendo un receptor AM, nos convendrá una frecuencia intermedia que sea muy fácilmente demodulable con los recursos de los que disponemos dentro de una FPGA. Pongámonos en el lado del transmisor y analicemos cómo es una señal modulada en AM:



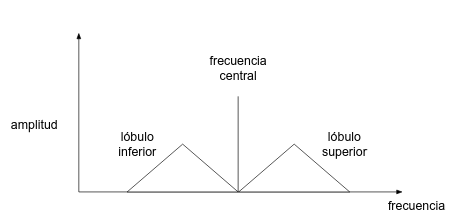
Cuando modulamos una señal senoidal de alta frecuencia (la frecuencia a la que emite la emisora o señal portadora) en amplitud usando una señal de baja frecuencia (música, voz, sonido, etc.), el resultado es una señal que sigue estando centrada en la portadora, pero que está acompañada de dos "lóbulos", uno hacia arriba y otro hacia abajo en el espectro: dichos lóbulos son la señal del sonido (señal moduladora) que modula a la señal portadora que se encuentra desplazada hasta esas zonas. Ambos "lóbulos" de modulación son simétricos.

Esto es, si, en el transmisor, yo emito a 576 KHz y modulo la señal en amplitud (AM) con un tono de 1 KHz estoy generando tres señales: una a 575 KHz, otra a 576 KHz (la portadora central de la banda, esta siempre estará) y otra a 577 KHz. Si al tono de 1 KHZ le añado otro tono de 2KHz se comenzarán a producir 5 señales en la antena: 574, 575, 576 (frecuencia central), 577 y 578 KHz. Como se puede apreciar el proceso de modulación AM es muy parecido al proceso de heterodinización, ya que se producen frecuencias sumas y resta (de hecho la modulación AM no deja de ser también una multiplicación de señales).

Cuando en el receptor desplazamos la señal al mezclarse (multiplicarse) con la señal del oscilador local, desplazamos todo por igual. Por ejemplo, supongamos que dentro de la FPGA queremos adoptar el mismo estándar que se utiliza en circuitería analógica y queremos desplazar hasta 455 KHz. Si queremos sintonizar una emisora que emite a 576 KHz podríamos hacer que un oscilador local (ya veremos cómo implementarlo) genere una señal a 1031 KHz, esto generará a la salida del multiplicador, dos señales, una a 455 KHz y otra a 1607 KHz (esta última habría que eliminarla mediante filtros digitales). Una vez aislada la señal de 455 KHz podremos realizar el proceso de demodulación.

Si esta emisora que emite a 576 KHz transmite en AM un tono a 1 KHz, tras ese proceso de mezcla y filtrado dentro de la FPGA tendremos dicho tono en 456 KHz, que habrá que extraerlo mediante alguna técnica DSP.

Zero-IF

¿No podríamos hacer algo para simplificar todo este proceso de mezclado a frecuencia intermedia seguido de demodulación de la frecuencia intermedia? Bueno, lo cierto es que, si estamos en AM, sí que se puede simplificar. Recordemos lo que comentamos antes de que cuando una emisora emite a 576 KHz y decide transmitir un tono a 1 KHz en AM, se radían tres señales: los 576 KHz de la frecuencia central y dos señales más y superpuestas a 575 y 577 KHz. La técnica Zero-IF (o "frecuencia intermedia cero") consiste en multiplicar la señal de la antena por una señal con EXACTAMENTE LA MISMA frecuencia que la emisora que transmite: por las propiedades de la multiplicación de las señales, si yo multiplico una señal con una frecuencia $f_1$ por otra señal con la misma frecuencia $f_1$, el resultado son dos señales: una con frecuencia $f_1 + f_1 = 2 \times f_1$ y otra con FRECUENCIA CERO ($f_1 - f_1$). Es decir que si nuestra emisora, que emite a 576 KHz, transmite un tono a 1 KHz y nosotros en el receptor multiplicamos la señal de la antena por otra señal a exactamente 576 KHz, desplazaremos al cero la frecuencia central de la señal recibida (576 KHz), por lo que el tono de 1 KHz que la emisora transmite y que, en la señal recibida en la antena, estaba en los lóbulos de 575 y 577 KHz, a la salida de nuestro multiplicador se convertirá en ¡Un tono de 1 KHz! Es decir, estaremos haciendo una demodulación de AM, sin necesidad de frecuencias intermedias (455 KHz) ni de complicados algoritmos de demodulación.

Simplificando el multiplicador

Lo habitual, y para garantizar una buena calidad de recepción, es que el oscilador local genere una onda senoidal (o lo más parecido a ésta) y, de hecho, es la implementación habitual que se realiza de osciladores locales en otros proyectos SDR basados en FPGA: un oscilador local que genera una onda senoidar de N bits de resolución que se multiplica por la señal que llega de la antena y luego se filtra y se demodula. Sin embargo incluso en sintonizadores analógicos o híbridos se utiliza a veces el concepto de "mezclador de conmutación", es decir un multiplicador que multiplica una señal por una onda cuadrada: siendo esto no más que dejar pasar tal cual o cambiada de signo la señal original al ritmo que marca la onda cuadrada (matemáticamente se traduce en que, cuando la señal del oscilador local está a nivel alto, multiplico la señal de entrada por 1 y, cuando está a nivel bajo, multiplico la señal de entrada por -1) . El uso de mezcladores de conmutación está muy extendido puesto que simplifican el diseño de los osciladores (un oscilador de onda cuadrada siempre es más barato de calibrar y de implementar en un circuito digital que un oscilador de onda senoidal) con la contrapartida de que el filtrado debe hacerse mejor (debido a las componentes de alta frecuencia que se generan por ser una señal cuadrada).

En nuestro caso he optado por simplificar el mezclador (multiplicador) hasta su mínima expresión. Como comentamos antes, la salida del ADC es una señal de 1 bit (que puede ser 0 o 1), si hacemos que la salida de nuestro oscilador local sea también de 1 bit, al usar la técnica de la mezcla mediante conmutación (0 o 1), la multiplicación de dichas señales podrá implementarse mediante un circuito combinacional simple de 2 bits de entrada y 1 bit de salida. Si consideramos que nuestras señales no tienen componente de continua podemos asumir que un valor binario de 0 se corresponde con un valor físico -1 mientras que un valor binario de 1 se corresponde con un valor físico de +1:

Entrada ADC	Entrada oscilador	Salida mezclador (multiplicador)
-1	-1	+1
-1	+1	-1
+1	-1	-1
+1	+1	+1

Si traducimos estos valores a binario de nuevo:

Entrada ADC	Entrada oscilador	Salida mezclador (multiplicador)
0	0	1
0	1	0
1	0	0
1	1	1

Lo que tenemos es que podemos modelar el mezclador mediante ¡Una simple puerta XNOR!

En la siguiente gráfica se puede ver como, incluso con una simplificación tan extrema como ésta (usando señales de 1 bit tanto para la señal delta-sigma como para la señal del oscilador local y "multiplicando" con una puerta XNOR), podemos conseguir un desplazamiento de frecuencia de la misma forma que si lo hiciésemos con un multiplicador "de verdad".



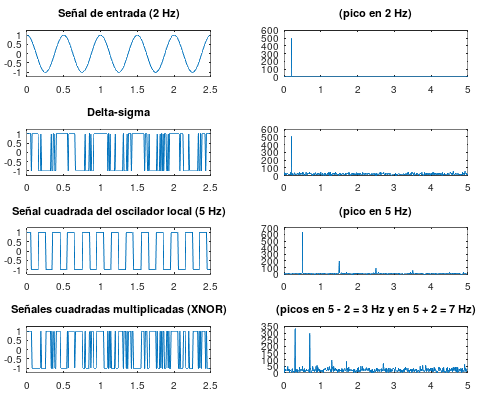
Se ha simulado, por simplicidad, que la señal de entrada (de antena) es de 2 Hz y que la señal del oscilador local es de 5 Hz. La primera columna se corresponde con el dominio del tiempo mientras que la segunda columna se corresponde con el dominio de la frecuencia:

1.- Al principio tenemos una señal senoidal normal de 2 Hz.

2.- A continuación calculamos una señal delta-sigma a partir de esa señal de entrada de 2 Hz (en la Wikipedia se explican ampliamente los principios de esta modulación pero podemos quedarnos con esta pequeña gráfica que resume en qué consiste esta modulación, que es lo que hace nuestro ADC).

3.- Por otro lado tenemos el oscilador local de onda cuadrada que, en este ejemplo, lo hemos puesto a 5 Hz.

4.- Multiplicamos ambas señales (XNOR) y el resultado, como se puede comprobar en las gráficas, es el deseado: se generan dos frecuencias, una suma (7 Hz) y otra resta (3 Hz), de las frecuencias de las dos señales de entrada (antena y oscilador local).

Implementación en la FPGA



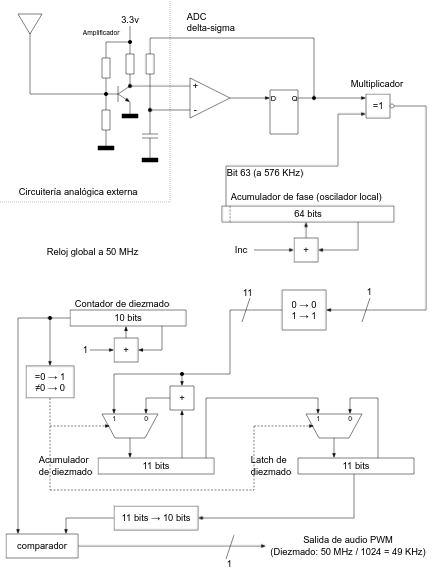
Para el ADC delta-sigma se sigue una configuración estándar como la descrita en esta publicación anterior y se calcula el valor de la resistencia y del condensador de integración en función de la frecuencia de reloj de la FPGA (50 MHz) usando el criterio publicado por Lattice Semiconductor:

$$200 < R \times C \times f_{clk} < 1000$$

Para nuestro caso particular usamos los valores C = 10 nF y R = 1 K. Por otro lado tenemos el acumulador de fase que hace las veces de oscilador local y cuya constante de incremento se calcula a partir de la frecuencia queremos sintonizar (nótese que, como usamos la técnica Zero-IF, la frecuencia del oscilador local deberá ser exactamente la misma que la de la emisora que queremos sintonizar). Si queremos sintonizar 576 KHz (en mi caso es la frecuencia a la que emite Radio Nacional de España en Las Palmas de Gran Canaria) calcularemos la constante de incremento del acumulador de fase de la siguiente manera:

$$Inc = {576000 \over 50000000} \times 2^{64} = 212506491729134048$$

De esta manera en el bit 63 (el más significativo) del acumulador de fase tendremos una onda cuadrada con una frecuencia de 576 KHz. Como se comentó con anterioridad, la multiplicación la implementamos mediante una simple puerta XNOR entre el bit 63 del acumulador de fase (oscilador local de onda cuadrada) y el bit proveniente del ADC delta-sigma.

A la salida de la puerta XNOR (nuestro particular multiplicador) convertimos la señal de 1 bit en una señal de 11 bits apta para ser acumulada en el registro de diezmado (en algunos textos técnicos se hace referencia al "diezmado" como "decimación", a mi me gusta más el término "diezmado", ya que es la traducción más correcta del término "decimation" y creo que expresa mejor su cometido).

Lo que hace el acumulador de diezmado es ir sumando las muestras que llegan del multiplicador (la puerta XNOR) y cuando ha hecho 1024 sumas (o, lo que es lo mismo, cuando el contador de diezmado se desborda), se pasa el valor de la cuenta al latch de diezmado y se inicia el acumulador de diezmado de nuevo. ¿Cual es el resultado de esto? Lo que estamos haciendo es un "diezmado en tiempo" y convertir una señal con una frecuencia de muestreo de 50 MHz (los 0s y 1s que salen del multiplicador) en otra señal con una frecuencia de muestreo de ${50000000 \over {2^{10}}} = {50000000 \over 1024} = 48828.125 \simeq 49 \: KHz$. Con este diezmado en tiempo matamos dos pájaros de un tiro:

1.- Por un lado, hacemos un filtrado paso-bajo, ya que estamos "promediando" y generamos una muestra de salida por cada 1024 muestras de entrada.

2.- Por otro lado, ajustamos la frecuencia de muestreo de la señal a un valor aceptable para ser procesado por circuitos de audio.

La salida del latch de diezmado ya es apta para convertirla a PWM y sacarla por un altavoz.



Salida PWM

La parte de la salida PWM de la FPGA lo que hace es convertir la señal del latch de diezmado en un tren de pulsos PWM que se conecta directamente a un amplificador de audio externo. El bit de salida PWM se calcula comparando el valor del latch de diezmado con el contador de diezmado, lo que provoca que la anchura de los pulsos de salida (un único bit que va al amplificador) sea proporcional al valor del latch de diezmado. Este bit (modulado en PWM) puede atacar directamente a la entrada de cualquier amplificador de audio.

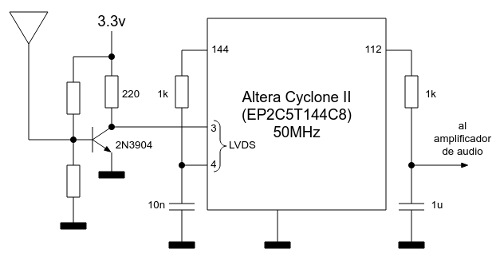
Esquema eléctrico final



Resultados

Los resultados distan mucho de considerarse de calidad, el ruido en la recepción es alto (sólo a mi se me ocurre montar un circuito de radio en una protoboard...), pero "se entiende" más o menos lo que dice :-). El amplificador de antena ha sido la parte que, de lejos, más trabajo me ha dado, ya que tengo que reconocer que mi fuerte no es la electrónica analógica y menos a estas frecuencias de trabajo.



El código fuente puede descargarse de la sección soft.

[ 2 comentarios ] ( 21854 visualizaciones )   |  [ 0 trackbacks ]   |  enlace permanente  |   ( 3 / 1030 )

---

La gestión de las interrupciones es un tema planteado de forma muy básica en la arquitectura original RISC-V. En controlador básico de interrupciones que se describe en los documentos oficiales de la arquitectura está más orientado a la captura de eventos entre diferentes niveles de ejecución que a la captura de eventos externos, algo que, en el caso de los microcontroladores, se echa de menos. Abordaremos el uso del este controlador básico de interrupciones y el uso del CLIC, un controlador de interrupciones más avanzado, que complementa al primero y que está disponible en casi todos los núcleos RISC-V.

Controlador básico de interrupciones

El control de interrupciones que se describe en el volumen 2 de la especificación es un control de interrupciones muy básico orientado más a la captura de eventos entre diferentes niveles de privilegio (captura desde el nivel supervisor de eventos producidos en el nivel usuario, o captura desde el nivel máquina de eventos producidos en el nivel supervisor) que a la captura de eventos externos. De hecho, en el controlador de interrupciones "oficial" sólo tenemos como "interrupciones" (tal y como las entendemos casi todos los que venimos del mundo de lo microcontroladores) dos tipos: las de timer y las etiquetadas genéricamente como "externas" (estas ultimas, dependientes de la implementación que haga cada fabricante).

Como se puede ver, se trata de un mecanismo de interrupción muy pobre y que, aunque muy bien pensado para entornos multiusuario, es insuficiente para entornos embebidos, en los que todo el código se ejecutará casi siempre con los niveles de privilegio M (de máquina) y apenas se usan otros niveles de privilegio. Sin embargo, en caso de que sólo necesitemos una interrupción de timer, sería la mejor opción, ya que está presente en todas las implementaciones de RISC-V (forma parte de la especificación estándar y siempre existirá).

Los CSR

Muchos de los parámetros de funcionamiento en los procesadores RISC-V se configuran mediante CSR (Control and Status Registers), dichos registros son registros internos del procesador que son accesibles mediantes instrucciones de esamblador especiales de transferencias de valores desde/hasta registros normales (CSRR, CSRW, etc.) o mediante valores inmediatos (CSRWI, etc.). Existen una serie de CSRs estándar y, además, cada fabricante puede incluir los suyos propios, siempre y cuando se mantengan los del estándar de RISC-V.


En este ejemplo de código el ensamblador que viene con las binutils sí reconoce el símbolo "mstatus" como CSR (al ser un CSR estándar presente en todos los núcleos RV32I), sin embargo el CSR "mtvt" es un CSR definido para el controlador de interrupciones avanzado (CLIC) y, como no está definido como símbolo en las "binutils", debemos poner su valor (0x307) si queremos acceder a él desde ensamblador.

Ejemplo 1: Blinker usando el mecanismo básico de interrupciones

Como dijimos antes, el mecanismo básico de interrupciones permite el uso de una interrupción de timer así como de una interrupción externa. En este caso usaremos este mecanismo básico de interrupciones para configurar la interrupción de timer con el objetivo de hacer parpadear un led.



Lo primero que hacemos es configurar en el CSR llamado "mtvec" el vector de interrupción, que podrá ser vectorizado o no, es decir, podremos indicar un puntero a una función o la dirección de memoria de una tabla donde estén indicadas, a su vez, las direcciones de salto de cada uno de las interrupciones que se definan (al estilo ARM Cortex-M). La forma en la que el RISC-V debe interpretar este valor (si como puntero a función o como puntero a tabla) se debe indicar en los dos bits menos significativos de este CSR. Como vamos a usar el mecanismo básico de interrupciones, la cantidad de interrupciones que se pueden generar es muy escaso y, por tanto, he optado por indicar directamente un puntero a una función (modo directo, mode = 00): Nótese que los bits 0 y 1 de la dirección de memoria de la función deben estar a 0 (puesto que estos bits en el CSR de mtvec se usan para indicar el modo), lo que obliga a que el handle de interrupción esté en una dirección de memoria múltiplo de 4 (alineada a 32 bits).

A continuación configuramos el CSR "mie" (Machine Interrupt Enable), donde decimos, para el nivel de privilegio M (el de máquina, con el que arranca el RISC-V por defecto) qué interrupciones se habilitan (activamos el bit correspondiente al timer):



En este CSR ponemos a 1 el bit 7 (MTIE = Machine Timer Interrupt Enable), mientras que en el CSR "mstatus" debemos habilitar las interrupciones de nivel de máquina poniendo a 1 el bit 3.



Con estos pasos ya tenemos configurado el controlador básico de interrupciones para que se dispare la interrupción de timer. El timer es muy parecido al SysTick de los procesadores ARM Cortex-M: un contador que se incrementa a la misma velocidad que el reloj del sistema y que, en el caso del RISC-V, se configura con dos registros mapeados en memoria:

- MTIME: Un registro de 64 bits que se va incrementando de forma indefinida y que cuando se desborda vuelve a cero (de lectura y escritura).

- MTIMECMP: Un registro de 64 bits que sólo se escribe desde software (aunque también es de lectura y escritura) y que, cuando vale igual que mtime, se produce la interrupción de timer en caso de estar ésta configurada.

Las direcciones de memoria donde están mapeados estos dos registros de 64 bits no están definidas por el estándar, son de libre elección por parte del fabricante. En el caso del GD32VF103, se alojan en 0xD1000000 y 0xD1000008 respectivamente.


Paso a comentar las partes más relevantes del código:

1. Definimos la función "interruptHandler" (aunque da igual el nombre que le pongamos), le ponemos los atributos de compilador "interrupt" y "section(".interrupt_handler")" (el nombre de la sección también da igual, lo importante es que no esté en la sección ".text" que es donde se pone por defecto todo el código). En la función reiniciamos los registro MTIME y MTIMECMP y cambiamos de estado el led. No es necesario marcar ningún flag para indicar que la interrupción está atendida ya que, según la documentación del estándar del RISC-V, al escribir en la dirección de memoria de MTIMECMP el procesador ya considera atendida la interrupción de timer.

2. En la función main habilitamos el reloj para la circuitería de GPIO, configuramos el puerto PC13 como salida push-pull a baja velocidad y configuramos la interrupción de timer: Escribimos en "mtvec" la dirección de memoria del handler que hemos definido antes (como estará alineado a 32 bits, sus dos bits menos significativos ya valdrán 0, por lo que, de paso, también seleccionamos que queremos un tratamiento de interrupciones no vectorizado, sino definiendo una única función para atender todas las interrupciones), habilitamos los bits de "mie" y "mstatus" que vimos antes y configuramos los registros MTIME y MTIMECMP para que el tiempo entre interrupciones sea de medio segundo (sabiendo que el reloj del timer va a 96 MHz / 4 = 24 MHz).

3. Entramos en un bucle infinito con la instrucción "wfi" para que el procesador permanezca dormido y en modo de bajo consumo mientras no esté atendiendo interrupciones.

Para que este código funcione correctamente es necesario, además de "startup.cc", que se encarga de inicializar todo el subsistema de relojes para que el núcleo vaya a 96 MHz, que en el linker script estén correctamente indicadas las secciones, sobre todo la sección que hemos llamado ".interrupt_handler", ya que debemos forzar a que dicha sección esté alineada a 32 bits (para que su dirección de memoria sea múltiplo de 4 y así los dos bits menos significativos de dicha dirección de memoria valgan 0).



Ejemplo 2: Blinker usando el CLIC (Core Local Interrupt Controller)

El CLIC (Core Local Interrupt Controller) es aún una propuesta de estándar, que se encuentra documentada en el GitHub de RISC-V International, pero que ya está siendo implementada por múltiples fabricantes, entre ellos GigaDevice (en su GD32VF103), SiFive (en todos sus procesadores) y muchos otros. Es una propuesta de controlador de interrupciones compatible con el sistema básico de interrupciones, pero que permite hasta 4096 interrupciones externas, configurables por niveles, prioridad, etc. Al ser una propuesta de la propia RISC-V International, lo cierto es que se ha convertido en estándar "de facto" y sólo cabe esperar que se acabe poniendo de forma "bonita" en un documento de especificación, en lugar de como está ahora. El CLIC define una serie de CSRs nuevos además de un conjunto de registros mapeados en memoria para el manejo "ampliado" de interrupciones.

En este caso, aunque el CLIC puede usarse con interrupciones no vectorizadas, es recomendable configurarlo para usarlas vectorizadas. En un CSR denominado "mclicbase" se encuentra la dirección de memoria base a partir de la que se localiza el resto de registros mapeados en memoria del CLIC. En el caso del GD32VF103 he optado por poner a fuego dicho valor, ya que es conocido (está indicado en la documentación del fabricante) y de esta forma también simplificamos el código generado (aunque sea menos portable). A partir de la dirección base del CLIC se obtiene el resto de registros mapeados en memoria.


Para configurar las interrupciones vectorizadas con el CLIC primero preparamos la tabla de interrupciones que, en el caso del GD32VF103, debe estar a partir de la dirección 0x00000000 (limitaciones del propio fabricante) y que nosotros situaremos a partir de la dirección 0x08000000, ya que ambas zonas de memoria son alias una de la otra y es a partir de 0x08000000 donde se encuentra la memoria flash de programa. Recordemos que en el caso del GD32VF103, la dirección de memoria 0x08000000 es la dirección de reset y que en esa posición lo que tenemos es una instrucción "jump" hacia 0x08000200 que es donde empieza la ejecución del código. Es en este "hueco" entre 0x08000000 y 0x08000200 es donde se aloja la tabla de vectores de interrupción. Como sólo vamos a configurar uno de los vectores de interrupción (el del timer, que se corresponde con la posición 7), hacemos que el linker script situe ahí (0x08000000 + (7 * 4) = 0x0800001C) la dirección de memoria de una sección que llamaremos ".clic_int_tmr" (el nombre no es relevante).


A continuación, en "main.cc" definimos nuestra función de manejo de las interrupciones:


También aplicamos a esta función el atributo "interrupt" e indicamos que dicha función debe estar en la sección ".clic_int_tmr" (el nombre que elegimos en el linker script). La única diferencia notable con respecto al caso del mecanismo básico de interrupciones es que aquí nos aseguramos de borrar de forma explícita el flag "interrupt pending" (IP) antes de regresar de la interrupción.

La preparación del CLIC es ligeramente más compleja que en el caso del mecanismo básico de interrupciones:


Los pasos son los siguientes:

1. Inicializamos el CLIC según indica la documentación: borrando CLIC_CFG, CLIC_MTH y poniendo a cero los 4096 registros de configuración mapeados en memoria.

2. Indicamos en el CSR "mtvec" que vamos a usar el CLIC en lugar del mecanismo básico de interrupciones poniendo a 1 los dos bits menos significativos de "mtvec". Recordemos que en el caso del mecanismo básico de interrupciones, estos dos bits estaban a 0.

3. Indicamos en el CSR "mstatus" que se habilitan las interrupciones a nivel de máquina (M). Igual que como hacíamos con el mecanismo básico de interrupciones.

4. Escribimos en un CSR nuevo definido para CLIC y llamado "mtvt" la dirección de memoria de la tabla de vectores de interrupción, que debe estar alineada a 64 bytes (en nuestro caso la dirección de memoria 0x08000000 cumple con este requisito). Nótese que el CSR "mtvt" no se reconoce por parte de las binutils de GNU, por lo que en el ensamblador generado hemos tenido que usar el valor numérico que corresponde con dicho CSR (0x307).

5. Configuramos en los registros del CLIC mapeados en memoria (en la posición correspondiente a la interrupción 7 de los 4096 registros), la prioridad, el tipo de interrupción y la propia habilitación de la misma (CLIC_ATTR, CLIC_IE, CLIC_IP y CLIC_CTL).

6. El resto de operaciones son las mismas que en caso del mecanismo básico de interrupciones de timer: inicializar MTIME y MTIMECMP y entrar en el bucle infinito en el que dormimos al procesador con la instrucción "wfi" cuando no está atendiendo interrupciones.

El resultado es el mismo: un led que parpadea, pero utilizando las dos aproximaciones distintas al mecanismo de interrupciones que permite hoy día la arquitectura RISC-V.

Todo el código está disponible en la sección soft.

[ 2 comentarios ] ( 5770 visualizaciones )   |  [ 0 trackbacks ]   |  enlace permanente  |   ( 3 / 1004 )

---

Partiendo del compilador cruzado GCC para RISC-V descrito en el post anterior, el primer objetivo será hacer una prueba de concepto con un procesador RISC-V real. En este caso he optado por un GD32VF103, un microcontrolador de GigaDevice, con 128 Kb de memoria flash de programa, 32 Kb de SRAM, procesador RISC-V con arquitectura básica RV32IMAC y periféricos muy parecidos a los del STM32F103.

Secuencia de arranque

Los procesadores RISC-V, al contrario que los ARM, no poseen, en su configuración base, un vector de interrupciones, es una extensión estándar pero no forma parte del núcleo en sí. Por tanto, el concepto que existe en los ARM de una tabla de interrupciones en la que el "reset" es una interrupción más, no existe en RISC-V: En los RISC-V existe el "RESET_VECTOR", que es la dirección de memoria desde donde arranca el procesador cuando se reinicia o se enciende. Dicha dirección suele ser 0x00000000 pero puede ser libremente definida por el fabricante, en el caso que nos ocupa, el GD32VF103 incluye un bootloader en la dirección 0x00000000, mientras que en la dirección 0x08000000 se encuentra la memoria flash de programa (los 128 Kb). Cuando el micro arranca en modo bootloader (determinado por un pin), arranca desde la dirección 0x00000000 (RESET_VECTOR = 0x00000000), ejecuta el bootloader y éste se encarga de poner el micro en modo DFU a través del USB, mientras que cuando arranca en modo normal (sin bootloader), el micro arranca desde la dirección 0x08000000 (RESET_VECTOR = 0x08000000), donde se supone que debe estar el programa principal.

Algo parecido ocurre con el puntero de pila: Al contrario que los Cortex-M de ARM, en los RISC-V no existe una tabla que indique el valor que debe tener, en el momento del arranque, el registro de pila (SP), por lo que dicho registro debe ser cargado a mano mediante una instrucción en ensamblador. Por ejemplo, una secuencia de arranque mínima podría ser:

reset_vector:
    la sp, 0x20005000   ; la SRAM acaba en 0x20005000 y la pila "crece" hacia abajo
    call main           ; llamamos a la función main

Nótese que no se está teniendo el cuenta la inicialización de variables globales (incluidos los constructores de objetos globales), pero es un punto de partida.

Linker script y arranque

Basándonos en un post anterior hacemos un linker script básico y un código de arranque e inicialización para variables globales y constructores. En este caso, al principio del linker script dividimos el código generado en dos zonas:

- Una al principio, en 0x08000000, donde sólo alojaremos una instrucción de salto.

- Otra a partir de 0x08000200 donde alojaremos la inicialización y el resto del código (incluida la función main).

Esto lo hacemos así porque en el caso del GD32VF103 sí que existe, para la extensión de las interrupciones de RISC-V, una tabla de interrupciones que se extiende desde 0x0800000C hasta 0x080001FC, por lo que, para poder en un futuro usar ese vector de interrupciones, haremos que el grueso del código de aloje a partir de 0x08000200 y en 0x08000000 lo que ponemos es un salto incondicional a 0x08000200.

SECTIONS {
    . = 0x08000000 ;
    .text : {
        startup.o (.startup0)
    }
    . = 0x08000200 ;
    .text : {
        _linker_code = . ;
        startup.o (.startup1)
        *(.text)
        *(.text.*)
        *(.rodata*)
        *(.gnu.linkonce.t*)
        *(.gnu.linkonce.r*)
    }
    .preinit_array : {
        __preinit_array_start = . ;
        *(.preinit_array)
        __preinit_array_end = . ;
    }
    .init_array : {
        __init_array_start = . ;
        *(.init_array)
        __init_array_end = . ;
    }
    .fini_array : {
        __fini_array_start = . ;
        *(.fini_array)
        __fini_array_end = . ;
    }
    .ctors : {
        __CTOR_LIST__ = . ;
        LONG((__CTOR_END__ - __CTOR_LIST__) / 4 - 2)
        *(.ctors)
        LONG(0)
        __CTOR_END__ = . ;
    }
    .dtors : {
        __DTOR_LIST__ = . ;
        LONG((__DTOR_END__ - __DTOR_LIST__) / 4 - 2)
        *(.dtors)
        LONG(0)
        __DTOR_END__ = . ;
    }
...

Como se puede ver, se definen dos secciones al principio del linker script:

- Una a partir de la dirección 0x08000000 y en la que se alojará el código de las funciones etiquetadas con la sección ".startup0" del fichero startup.o.

- Otra a partir de la dirección 0x08000200 y en la que se alojará primero el código de las funciones que se encuentren etiquetadas con la sección ".startup1" seguido por el resto del código del programa.

A continuación se ubican las secciones estándar ".preinit_array", ".init_array", ".ctors" encargadas de alojar las llamadas a los constructores y las funciones de inicialización de variables globales, y las secciones estándar ".fini_array" y ".dtors", encargadas de alojar las llamadas a los destructores y las funciones de destrucción de variables globales (esta parte del código no se debería ejecutar jamás en un sistema embebido, se incluye por elegancia).

Variables globales en RAM y copia de datos de Flash a RAM

...
    flash_sdata = . ;
    . = 0x20000000 ;
    ram_sdata = . ;
    .data : AT (flash_sdata) {
        _linker_data = . ;
        *(.data)
        *(.data.*)
        *(.gnu.linkonce.d*)
    }
    ram_edata = . ;
    data_size = ram_edata - ram_sdata;
    ram_sbssdata = . ;
    .bss : AT (LOADADDR(.data) + SIZEOF(.data)) {
        _linker_bss = . ;
        *(.bss)
        *(.bss.*)
        *(.gnu.linkonce.b.*)
        *(.COMMON)
    }
    ram_ebssdata = . ;
    bssdata_size = ram_ebssdata - ram_sbssdata;
    _linker_end = . ;
    end = . ;
}

En esta parte del linker script se indica que la dirección virtual de los datos es 0x20000000 (esta es la dirección que se usará desde el código de programa para acceder a los datos en RAM), pero sin embargo dichos datos están inicialmente alojados en la memoria flash (a continuación de la sección ".dtors"), por lo que es necesario un copiado de dichas variables globales inicializadas desde la memoria flash hasta la RAM antes de que se ejecute la función "main".

Código de arranque

En el fichero startup.cc se definen dos funciones _startup_0 y _startup_1 y se etiquetan como de las secciones ".startup0" y ".startup1", respectivamente. La función _startup_0 está definida con el atributo "naked" (para que el compilador no genere código de preámbulo ni postámbulo) y contiene una única instrucción de salto:


Esta es la función que se aloja en la dirección 0x08000000 y que, como se vio antes, es la encargada de saltar a _startup_1. La función _startup_1, que también está definida como "naked" pero etiquetada en la sección ".startup1" (por lo que se aloja a partir de la dirección 0x08000200) alberga el resto de código de inicialización:


Y realiza lo siguiente:

1. Inicializa el puntero de pila para que apunte al final de la RAM (el puntero de pila se decrementa cuando se hace "push" y se incrementa cuando se hace "pop").

2. Inicializa los PLLs del microcontrolador para configurar el reloj de cristal (en mi caso he dejado esta función vacía por lo que el microcontrolador queda funcionando con el reloj RC interno que es más lento pero suficiente para nuestro blinker).

3. Inicializa la RAM que se copia desde la flash (ver aquí los detalles de este proceso).

4. Inicializa la RAM que debe estar a cero (BSS).

5. Invoca las funciones de inicialización y los constructores.

6. Finalmente incova a la función "main".

Al final se coloca una especie de código "de cortesía" para que, en el caso de que la función "main" regrese (cosa que no debería ocurrir), se invoquen los destructores y el micro se quede "colgado" (bucle infinito).

Prueba de concepto

Se ha optado por hacer un simple blinker basado en esperas estándar de ciclos de procesador, en lugar de un timer, ya que, como se comentó antes, el núcleo básico de un RISC-V no incluye interrupciones y creo que es mejor abordarlas en una siguiente entrega:


La placa en la que está alojada el GD32VF103 es una Longan Nano que posee un led tricolor con la componente roja conectada al pin PC13 del micro. Para hacer parpadear este led rojo debemos:

1. Habilitar el reloj interno de la circuitería GPIO del micro.

2. Configurar el pin PC13 como GPIO de salida en push-pull.

3. Modificar el bit 13 del registro asociado de forma periódica para hacer que el led parpadee.

Los registros son una copia casi exacta de los del STM32F103 por lo que si estás acostumbrado a ese micro de ST, adaptarte al GD32VF103 será muy sencillo.

Bootloader

Cuando arranca el microcontrolador GD32VF103, si el pin BOOT0 se encuentra a nivel 1, no se arranca desde la dirección 0x08000000, sino que se ejecuta un "bootloader" interno que configura el microcontrolador como un dispositivo USB con interfaz estándar DFU (Device Firmware Upgrade). Se trata de un estándar conocido y para el que existen herramientas como dfu-util (que, en el caso de Linux, sólo requiere de la librería "libusb"). Con el microcontrolador en modo DFU y el comando "dfu-util" podemos "tostar" nuestro ejecutable "main.bin" de forma muy sencilla:

dfu-util --dfuse-address 0x08000000 -D main.bin

En la sección soft está todo el código disponible.



[ añadir comentario ] ( 1220 visualizaciones )   |  [ 0 trackbacks ]   |  enlace permanente  |   ( 3 / 984 )

---

Los procesadores RISC-V empiezan a hacerse poco a poco un huequito en nuestros corazones. A continuación pongo las instrucciones para compilar la toolchain cruzada de GNU (GCC) para RISC-V con newlib.

Se trata de una toolchain para sistemas "bare metal", sin sistema operativo, por lo que no tiene soporte para multihilos ni para librerías dinámicas.

binutils 2.36

mkdir -p /opt/baremetalriscv/src
mkdir -p /opt/baremetalriscv/build
cd /opt/baremetalriscv/src
wget https://ftp.gnu.org/gnu/binutils/binutils-2.36.tar.bz2
tar xf binutils-2.36.tar.bz2
cd ../build
mkdir binutils-2.36
cd binutils-2.36/
../../src/binutils-2.36/configure --prefix=/opt/baremetalriscv --target=riscv32-none-elf --disable-nls
make
make install

gcc 11.1.0 (stage 1)

cd /opt/baremetalriscv/src
wget https://ftp.gnu.org/gnu/gcc/gcc-11.1.0/gcc-11.1.0.tar.gz
wget https://ftp.gnu.org/gnu/gmp/gmp-6.2.1.tar.bz2
wget https://ftp.gnu.org/gnu/mpc/mpc-1.2.1.tar.gz
wget https://ftp.gnu.org/gnu/mpfr/mpfr-4.1.0.tar.gz
tar xf gcc-11.1.0.tar.gz 
tar xf gmp-6.2.1.tar.bz2 
tar xf mpc-1.2.1.tar.gz
tar xf mpfr-4.1.0.tar.gz
mv gmp-6.2.1 gcc-11.1.0/gmp
mv mpc-1.2.1 gcc-11.1.0/mpc
mv mpfr-4.1.0 gcc-11.1.0/mpfr
cd ../build/
mkdir gcc-11.1.0-stage-1
cd gcc-11.1.0-stage-1/
export PATH=/opt/baremetalriscv/bin:${PATH}
../../src/gcc-11.1.0/configure --prefix=/opt/baremetalriscv --target=riscv32-none-elf --enable-languages=c --without-headers --disable-nls --disable-threads --disable-shared --disable-libssp --with-newlib
make all-gcc all-target-libgcc
make install-gcc install-target-libgcc

newlib

cd /opt/baremetalriscv/src
git clone git://github.com/riscv/riscv-newlib.git
cd ../build
mkdir newlib
cd newlib
../../src/riscv-newlib/configure --prefix=/opt/baremetalriscv --target=riscv32-none-elf
make
make install

gcc 11.1.0 (stage 2)

cd /opt/baremetalriscv/build
mkdir gcc-11.1.0-stage-2
cd gcc-11.1.0-stage-2/
../../src/gcc-11.1.0/configure --prefix=/opt/baremetalriscv --target=riscv32-none-elf --enable-languages=c,c++ --disable-nls --disable-threads --disable-shared --disable-libssp --with-newlib --with-headers=../../src/riscv-newlib/newlib/libc/include
make
make install

El compilador de C++ de GCC 11.1 compila por defecto en modo C++17 y soporta prácticamente todo el estándar C++20.

ACTUALIZACIÓN: El proceso de compilación descrito sirve también para gcc-12.2, binutils-2.40 y el repositorio de newlib oficial (git://sourceware.org/git/newlib-cygwin.git) puesto que el proyecto riscv-newlib ya se ha integrado en el proyecto oficial de newlib.

[ añadir comentario ] ( 795 visualizaciones )   |  [ 0 trackbacks ]   |  enlace permanente  |   ( 3 / 920 )

---

La literatura existente relacionada con el diseño de filtros digitales suele incidir en el estudio de determinados filtros ya conocidos, como paso-bajo, paso-alto, paso-banda, etc., a veces calculados a partir de la discretización de filtros analógicos y sin entrar en detalles de diseño o sin abordar el problema de forma directa (sin discretizar). A lo largo de este artículo se abordará el diseño directo de un filtro resonante sencillo.

Plano z

La herramienta fundamental para el cálculo de filtros digitales es la transformada Z y su plano complejo asociado, denominado "plano z". Se asume que el lector está medianamente familiarizado con la transformada z y no se abordarán los detalles ni las propiedades de la misma.

La transformada z transforma una función, situada en el dominio discreto del tiempo $x[n]$, en otra función, situada en el dominio complejo de z $X(z)$. Esta transformación es equivalente a la transformada de Laplace en el dominio continuo y tiene ambas propiedades similares en cuanto a linealidad y estabilidad. Al igual que la transformada de Laplace, la transformada Z también se utiliza para modelar funciones de transferencia de sistemas, en el caso de la transformada Z, son sistemas discretos.

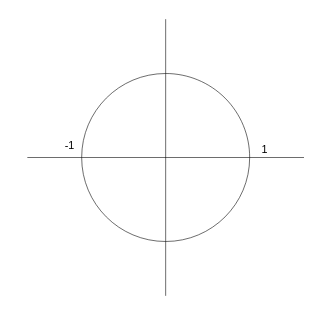
Es decir, si para un filtro analógico tenemos una función de transferencia $H(s)$, caracterizada principalmente por sus ceros y sus polos, para un filtro digital tendremos también una función de transferencia $H(z)$, caracterizada también por sus ceros y sus polos. Tanto en el caso de Laplace como en el caso Z los ceros determinan para qué tipo de señales el filtro "tiende a cancelar la entrada" y los polos determinan para qué tipo de señales el filtro "tiende a amplificar la entrada" o incluso entrar en resonancia. La regla básica que debe cumplirse en un filtro analógico es que los polos de $H(s)$ nunca deben tener parte real positiva (deben estar siempre localizados en el semiplano izquierdo del plano complejo $s$), mientras que en caso de un filtro digital, los polos de $H(z)$ nunca deben alojarse fuera de la circunferencia unitaria centrada en el origen del plano complejo $z$ (es decir, los polos en un filtro digital deben cumplir que $|z| < 1$).

Diseño de un filtro resonante sencillo

En el plano z no se mapean frecuencias absolutas como en el plano s, sino que se mapean frecuencias "relativas" a la frecuencia de muestreo y a lo largo de la longitud de la circunferencia de radio 1. La frecuencia asociada a un valor complejo del plano z se corresponde con el ángulo (argumento) de dicho valor: un ángulo de 0 radianes se corresponde con un valor en continua (0 Hz) mientras que un valor de $\pi$ radianes se corresponde con la mitad de la frecuencia de muestreo (frecuencia Nyquist). Si, por ejemplo, muestreamos a 44100 Hz, la frecuencia máxima ($\pi$) será de 22050 Hz, mientras que si muestreamos a 8000 Hz la misma frecuencia PI se corresponderá con 4000 Hz.



El diseño básico de filtros digitales es muy sencillo y se resume en cuatro reglas principales:


- Alojar tantos ceros sobre la circunferencia de radio 1 como frecuencias queramos cancelar. Lo importante de cada cero será su ángulo (= frecuencia) con respecto al origen. Por ejemplo si colocamos un cero en en punto $z = 1$, que se corresponde con un ángulo de 0 radianes, nuestro filtro eliminará la componente de continua de la señal.

- Alojar tantos polos DENTRO de la circunferencia de radio 1 ($|z| < 1$) como frecuencias queramos amplificar. En este caso es importante tanto el ángulo (= frecuencia que queremos reforzar) como su magnitud o módulo (= nivel de refuerzo). Si hacemos que la magnitud (el módulo) de un polo sea 1 ($|z| = 1$) el filtro auto-oscilará a esa frecuencia. Por ejemplo, si colocamos un polo en $z = -1$, que se corresponde con un ángulo $\pi$, estaremos reforzando las señales con frecuencia próxima a $\pi$ (= la mitad de la frecuencia de muestreo).

- Los polos y ceros que tengan parte imaginaria diferente de 0 deberán ponerse por pares conjugados para poder trabajar con señales reales (sin componente imaginaria). Por ejemplo, si estamos muestreando a 44100 Hz y queremos cancelar las frecuencias próximas a 11025 Hz (frecuencia ${\pi \over 2}$), debemos colocar DOS polos conjugados: uno en $(0, 1)$, formando un ángulo de 90 grados (${\pi \over 2}$) y otro en $(0, -1)$ (su conjugado).

- Al final lo habitual es también ajustar la ganancia global del filtro (aunque en este caso no lo hemos hecho por simplicidad). Esto se hace habitualmente debido a que a veces los polos meten mucha ganancia en la banda de paso y es necesario escalar la salida antes de emitirla o la entrada antes de procesarla.


Si, por ejemplo, queremos hacer un filtro paso bajo, lo habitual, es poner un cero en $z = -1$ (sobre la circunferencia de radio 1 con ángulo $\pi$) con el objetivo de anular las altas frecuencias y un polo (con su complejo conjugado) cerca de la frecuencia de corte de nuestro filtro. En nuestro caso de estudio, se trata de un filtro resonante sencillo, por lo que definiremos dos ceros: uno en $z = 1$ (0 radianes), y otro en $z = -1$, ($\pi$ radianes). Como queremos una única frecuencia de resonancia, definimos un único polo (junto con su complejo conjugado, por lo que realmente serán dos polos).



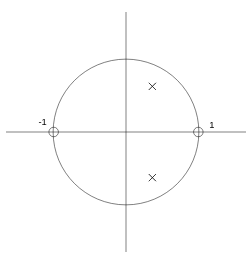
Con esta configuración de dos ceros reales en -1 y 1 y dos polos complejos conjugados en la frecuencia de resonancia tenemos la siguiente función de transferencia en Z:

$$H(z) = {(z + 1)(z - 1) \over (z - p_1)(z - p_1^\prime)}$$

Para la que se cumple que:

$$p_1 = a + bi \;\;\;\;\;\;\;\;\; p_1^\prime = a - bi$$

Desarrollando el denominador (los polos) de $H(z)$ tenemos que:

$$(z - p_1)(z - p_1^\prime) = z(z - p_1^\prime) - p_1(z - p_1^\prime)$$
$$ = z^2 - zp_1^\prime -p_1z + p_1p_1^\prime$$
$$ = z^2 - z(p_1^\prime + p_1) + p_1p_1^\prime$$
$$ = z^2 - z2a + p_1p_1^\prime$$
$$ = z^2 - z2a + a^2 + b^2$$

Nótese que, al ser los polos complejos conjugados, las operaciones
$(p_1^\prime + p_1)$ y $p_1p_1^\prime$ dan como resultado, valores reales (sin componente imaginaria). Por otro lado, si desarrollamos el numerador (los ceros) de $H(z)$ tenemos que:

$$(z + 1)(z - 1) = z(z - 1) + (z - 1)$$
$$ = z^2 - z + z - 1$$
$$ = z^2 - 1$$

Por tanto la función de transferencia $H(z)$ puede reescribirse de la siguiente manera:

$$H(z) = {{z^2 - 1} \over {z^2 - z2a + a^2 + b^2}}$$

Podemos visualizar la respuesta en frecuencia de este sistema asignando a z diferentes valores sobre la circunferencia unitaria $z = e^{iw} = cos(w) + i sen(w)$:



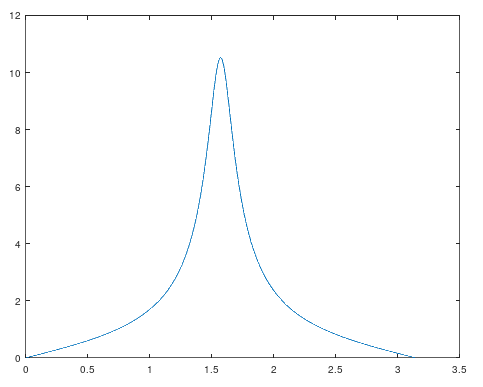
Para generar esta gráfica se ejecutó el siguiente código octave que sitúa el polo (= la frecuencia de resonancia del filtro) en ${\pi \over 2}$:



Implementación del filtro

Ahora que ya tenemos la función de transferencia en el dominio Z del filtro que queremos, el siguiente paso es pasar al dominio discreto y calcular los coeficientes en diferencias finitas para poder implementarlo. Lo primero que se hace es evitar que haya exponentes mayores que 0 para z (exponentes positivos de z se corresponden a muestras "futuras" en el tiempo). Esto se soluciona de forma muy sencilla multiplicando numerador y denominador de $H(z)$ por $z^{-2}$, esto mantiene $H(z)$ igual pero elimina los exponentes positivos:

$$H(z) = {{z^2 - 1} \over {z^2 - z2a + a^2 + b^2}}$$
$$H(z) = {{z^{-2}(z^2 - 1)} \over {z^{-2}(z^2 - z2a + a^2 + b^2)}}$$
$$H(z) = {{1 - z^{-2}} \over {1 - z^{-1}2a + z^{-2}(a^2 + b^2)}}$$

Ahora ya podemos calcular los coeficientes de forma más sencilla. Como $H(z)$ es una función de transferencia en Z tenemos que, si $X(z)$ es la transformada Z de la entrada e $Y(z)$ es la transformada Z de la salida, entonces:

$$Y(z) = H(z) X(z) = {{1 - z^{-2}} \over {1 - z^{-1}2a + z^{-2}(a^2 + b^2)}} X(z)$$

Y, por tanto:

$$Y(z)(1 - z^{-1}2a + z^{-2}(a^2 + b^2)) = X(z)(1 - z^{-2})$$
$$Y(z)-Y(z)z^{-1}2a+Y(z)z^{-2}(a^2 + b^2) = X(z) - X(z)z^{-2}$$

Como la transformada Z es lineal y se cumple que la transformada Z de un valor desplazado k muestras en el tiempo es la siguiente:

$$Z \left\{ x[n - k] \right\} = X(z)z^{-k}$$

Entonces podemos hacer la antitransformada Z de forma sencilla:

$$y[n] - y[n - 1]2a + y[n - 2](a^2 + b^2) = x[n] - x[n - 2]$$

Y, despejando $y[n]$ tenemos que:

$$y[n] = x[n] - x[n - 2] + y[n - 1]2a - y[n - 2](a^2 + b^2)$$

Esto, como se puede ver, es una ecuación en diferencias finitas, que es muy fácil de implementar tanto en hardware como en software. Veamos una ejemplo de código octave que genera ruido blanco y luego lo hace pasar por el filtro (aplica la ecuación en diferencias finitas con los mismos valores a y b, esto es, misma frecuencia de resonancia en ${\pi \over 2}$).



A continuación se pueden ver las señales y los espectros en frecuencia de las mismas y se puede comprobar como el funcionamiento del filtro es el esperado:



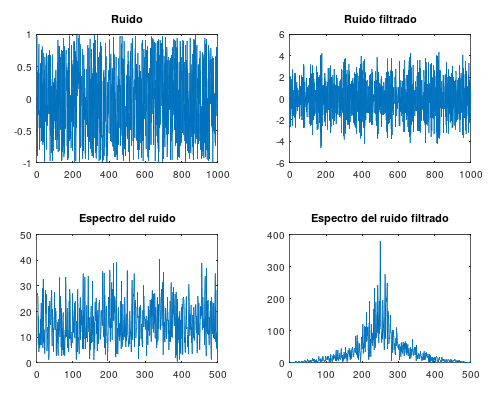
[ añadir comentario ] ( 1731 visualizaciones )   |  [ 0 trackbacks ]   |  enlace permanente  |   ( 2.9 / 969 )

---

<< <Anterior | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | Siguiente> >>

- Página generada en 0.2664 segundos | Site Views: 172665