Heterodinización
El proceso de heterodinización consiste en trasladar la frecuencia de una emisora que queremos sintonizar a otra frecuencia que es más cómoda a nivel electrónico o de procesamiento, para demodular. Este proceso se consigue en circuitería analógica normalmente mediante lo que se denomina un mezclador (multiplicador) en combinación con un oscilador: Si multiplicamos la señal que llega de una antena por una señal sinusoidal de un oscilador local conseguimos realizar un desplazamiento de todas las frecuencias que llegan a la antena de tal manera que si tenemos una emisora en $f_1$ y nuestro oscilador local genera una señal en $f_2$, el resultado serán dos señales con las mismas características que $f_1$ pero desplazadas en frecuencia: una en $f_1 + f_2$ y otra en $f_1 - f_2$.
Si denominamos a $f_1 - f_2 = f_i$ frecuencia intermedia podemos dejar pasar sólo dicha frecuencia mediante un filtro paso-banda (con la ventaja añadida de que dicho filtro es de frecuencia fija) y realizar todo el proceso de demodulación basándonos sólo en esta frecuencia intermedia, independientemente de a qué frecuencia esté emitiendo la emisora (independientemente de $f_1$) puesto que con el mezclador y el oscilador local ya desplazamos la señal de la emisora como si emitiese en $f_i$. En los receptores superheterodinos lo que se hace normalmente es elegir una frecuencia $f_i$ relativamente cómoda (el estándar es 455 KHz para AM y 10.7 MHz para FM). De esta manera, por ejemplo, para un receptor AM comercial que deba recibir emisoras en la banda entre 530 y 1710 KHz, su oscilador local generará frecuencias en el rango de 985 a 2165 KHz; así, para recibir una emisora que emita a 576 KHz, el receptor generará una señal en su oscilador local de 1031 KHz que, al ser multiplicada por la señal de antena, proporcionará un par de frecuencias resultado de esa multiplicación estando una de dichas frecuencias en 455 KHz. Y así con cualquier emisora: basta con alterar la frecuencia del oscilador local para cambiar de emisora, el resto de la circuitería del receptor trabaja a 455 KHz.
Implementación en digital
Como objetivo inicial nos planteamos un receptor sencillo AM para la banda comercial, puesto que la demodulación en amplitud suele ser un proceso más sencillo que la demodulación en frecuencia (FM). Como se vio anteriormente el proceso de heterodinización consiste básicamente en multiplicar la señal de antena por otra señal procedente de un oscilador local. El primer escollo que nos encontramos es la lectura de la señal de la antena y su posterior conversión analógico-digital.
Amplificador analógico para la antena
El amplificador analógico de antena hace una amplificación de banda ancha (no sintonizada) pero necesaria para que el ADC pueda detectar señal. He utilizado una configuración estándar de amplificador en emisor común.
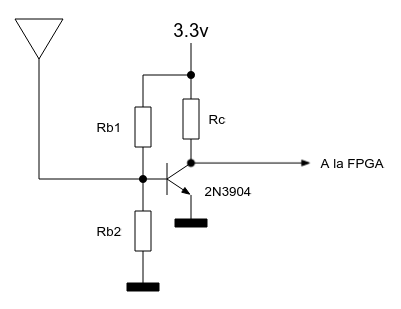
En las pruebas con el prototipo se optó por ajustar las dos resistencias de la base de forma empírica con un potenciómetro ajustable de 10 K en modo divisor de tensión hasta que la calidad fuera la mejor posible. Al usarse un transistor 2N3904 la resistencia del colector sí se calculó utilizando las curvas características:
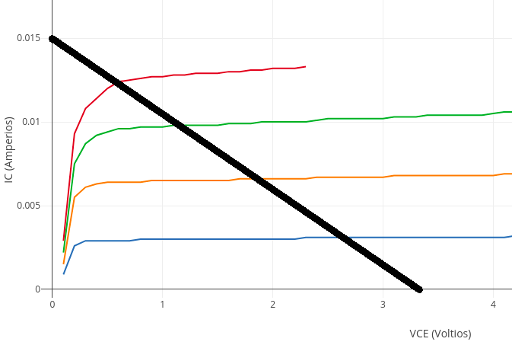
Usamos el valor de $220 \Omega$ para $R_c$ puesto que con ese valor tenemos una recta de carga con mínima distorsión y ganancia razonable, que toca, en el eje X, al punto $V_{cc} = 3.3 V$ y, en el eje Y, al punto ${3.3 \over 220} = 0.015 A$.
ADC para la entrada de la antena
Tratamos de usar una conversión "barata" de tipo delta-sigma, de la que hablamos en una entrada anterior, usando un comparador LVDS interno de la FPGA (todas las FPGA vienen con entradas diferenciales incorporadas basadas en comparadores LVDS). Este tipo de conversión es muy eficiente, permite resolución arbitraria pero, a cambio, requiere mucho sobremuestreo (oversampling) para obtener lecturas fiables. Al tener nuestra FPGA un reloj a 50 MHz, el sobremuestreo nos puede resultar muy caro a efectos de ancho de banda: por ejemplo para obtener una resolución de 8 bits en el ADC ya no podríamos muestrear a 50 MHz, sino a ${50000000 \over {2^8}} = 195 \: KHz$ con lo cual el ancho de banda del ADC caería a los 97 KHz y ya nos iríamos fuera del rango de la banda AM que queríamos abarcar inicialmente.
¿Qué pasa si, manteniendo la frecuencia de reloj de 50 MHz, subimos la frecuencia de muestreo a costa de una pérdida de resolución en el ADC? Más aún ¿Qué pasa si nos vamos al caso extremo de poner la frecuencia de muestreo a 50 MHz y de considerar un ADC de 1 bit de resolución? Bueno, uno puede pensar, a priori que esa pérdida en los bits de resolución es inasumible, pero lo cierto es que, si el ADC es de tipo delta-sigma, aunque la resolución del ADC sea de 1 bit, la anchura de los pulsos será proporcional al nivel de la entrada y, a nivel espectral, la señal de entrada seguirá siendo fiel reflejo de lo que llega por la antena, al menos hasta cierta frecuencia. Bueno, probemos entonces con un ADC de 1 bit a ver qué tal.
Elección de la frecuencia intermedia
Como se vio al principio, en los circuitos electrónicos, lo usual es elegir frecuencias intermedias que sean cómodas de cara al cálculo de componentes, de cara a la minimización del ruido, precio, rendimiento, etc. Sin embargo si estamos realizando el mezclado (la multiplicación) de las señales y la posterior demodulación dentro de una FPGA, la elección de la frecuencia intermedia (los 455 KHz que elegimos para el receptor AM) se convierte en una elección totalmente arbitraria: podríamos elegir la frecuencia que quisiéramos. En el caso que nos ocupa, y siendo un receptor AM, nos convendrá una frecuencia intermedia que sea muy fácilmente demodulable con los recursos de los que disponemos dentro de una FPGA. Pongámonos en el lado del transmisor y analicemos cómo es una señal modulada en AM:
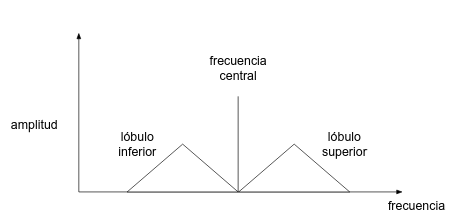
Cuando modulamos una señal senoidal de alta frecuencia (la frecuencia a la que emite la emisora o señal portadora) en amplitud usando una señal de baja frecuencia (música, voz, sonido, etc.), el resultado es una señal que sigue estando centrada en la portadora, pero que está acompañada de dos "lóbulos", uno hacia arriba y otro hacia abajo en el espectro: dichos lóbulos son la señal del sonido (señal moduladora) que modula a la señal portadora que se encuentra desplazada hasta esas zonas. Ambos "lóbulos" de modulación son simétricos.
Esto es, si, en el transmisor, yo emito a 576 KHz y modulo la señal en amplitud (AM) con un tono de 1 KHz estoy generando tres señales: una a 575 KHz, otra a 576 KHz (la portadora central de la banda, esta siempre estará) y otra a 577 KHz. Si al tono de 1 KHZ le añado otro tono de 2KHz se comenzarán a producir 5 señales en la antena: 574, 575, 576 (frecuencia central), 577 y 578 KHz. Como se puede apreciar el proceso de modulación AM es muy parecido al proceso de heterodinización, ya que se producen frecuencias sumas y resta (de hecho la modulación AM no deja de ser también una multiplicación de señales).
Cuando en el receptor desplazamos la señal al mezclarse (multiplicarse) con la señal del oscilador local, desplazamos todo por igual. Por ejemplo, supongamos que dentro de la FPGA queremos adoptar el mismo estándar que se utiliza en circuitería analógica y queremos desplazar hasta 455 KHz. Si queremos sintonizar una emisora que emite a 576 KHz podríamos hacer que un oscilador local (ya veremos cómo implementarlo) genere una señal a 1031 KHz, esto generará a la salida del multiplicador, dos señales, una a 455 KHz y otra a 1607 KHz (esta última habría que eliminarla mediante filtros digitales). Una vez aislada la señal de 455 KHz podremos realizar el proceso de demodulación.
Si esta emisora que emite a 576 KHz transmite en AM un tono a 1 KHz, tras ese proceso de mezcla y filtrado dentro de la FPGA tendremos dicho tono en 456 KHz, que habrá que extraerlo mediante alguna técnica DSP.
Zero-IF
¿No podríamos hacer algo para simplificar todo este proceso de mezclado a frecuencia intermedia seguido de demodulación de la frecuencia intermedia? Bueno, lo cierto es que, si estamos en AM, sí que se puede simplificar. Recordemos lo que comentamos antes de que cuando una emisora emite a 576 KHz y decide transmitir un tono a 1 KHz en AM, se radían tres señales: los 576 KHz de la frecuencia central y dos señales más y superpuestas a 575 y 577 KHz. La técnica Zero-IF (o "frecuencia intermedia cero") consiste en multiplicar la señal de la antena por una señal con EXACTAMENTE LA MISMA frecuencia que la emisora que transmite: por las propiedades de la multiplicación de las señales, si yo multiplico una señal con una frecuencia $f_1$ por otra señal con la misma frecuencia $f_1$, el resultado son dos señales: una con frecuencia $f_1 + f_1 = 2 \times f_1$ y otra con FRECUENCIA CERO ($f_1 - f_1$). Es decir que si nuestra emisora, que emite a 576 KHz, transmite un tono a 1 KHz y nosotros en el receptor multiplicamos la señal de la antena por otra señal a exactamente 576 KHz, desplazaremos al cero la frecuencia central de la señal recibida (576 KHz), por lo que el tono de 1 KHz que la emisora transmite y que, en la señal recibida en la antena, estaba en los lóbulos de 575 y 577 KHz, a la salida de nuestro multiplicador se convertirá en ¡Un tono de 1 KHz! Es decir, estaremos haciendo una demodulación de AM, sin necesidad de frecuencias intermedias (455 KHz) ni de complicados algoritmos de demodulación.
Simplificando el multiplicador
Lo habitual, y para garantizar una buena calidad de recepción, es que el oscilador local genere una onda senoidal (o lo más parecido a ésta) y, de hecho, es la implementación habitual que se realiza de osciladores locales en otros proyectos SDR basados en FPGA: un oscilador local que genera una onda senoidar de N bits de resolución que se multiplica por la señal que llega de la antena y luego se filtra y se demodula. Sin embargo incluso en sintonizadores analógicos o híbridos se utiliza a veces el concepto de "mezclador de conmutación", es decir un multiplicador que multiplica una señal por una onda cuadrada: siendo esto no más que dejar pasar tal cual o cambiada de signo la señal original al ritmo que marca la onda cuadrada (matemáticamente se traduce en que, cuando la señal del oscilador local está a nivel alto, multiplico la señal de entrada por 1 y, cuando está a nivel bajo, multiplico la señal de entrada por -1) . El uso de mezcladores de conmutación está muy extendido puesto que simplifican el diseño de los osciladores (un oscilador de onda cuadrada siempre es más barato de calibrar y de implementar en un circuito digital que un oscilador de onda senoidal) con la contrapartida de que el filtrado debe hacerse mejor (debido a las componentes de alta frecuencia que se generan por ser una señal cuadrada).
En nuestro caso he optado por simplificar el mezclador (multiplicador) hasta su mínima expresión. Como comentamos antes, la salida del ADC es una señal de 1 bit (que puede ser 0 o 1), si hacemos que la salida de nuestro oscilador local sea también de 1 bit, al usar la técnica de la mezcla mediante conmutación (0 o 1), la multiplicación de dichas señales podrá implementarse mediante un circuito combinacional simple de 2 bits de entrada y 1 bit de salida. Si consideramos que nuestras señales no tienen componente de continua podemos asumir que un valor binario de 0 se corresponde con un valor físico -1 mientras que un valor binario de 1 se corresponde con un valor físico de +1:
| Entrada ADC | Entrada oscilador | Salida mezclador (multiplicador) |
|---|---|---|
| -1 | -1 | +1 |
| -1 | +1 | -1 |
| +1 | -1 | -1 |
| +1 | +1 | +1 |
Si traducimos estos valores a binario de nuevo:
| Entrada ADC | Entrada oscilador | Salida mezclador (multiplicador) |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Lo que tenemos es que podemos modelar el mezclador mediante ¡Una simple puerta XNOR!
En la siguiente gráfica se puede ver como, incluso con una simplificación tan extrema como ésta (usando señales de 1 bit tanto para la señal delta-sigma como para la señal del oscilador local y "multiplicando" con una puerta XNOR), podemos conseguir un desplazamiento de frecuencia de la misma forma que si lo hiciésemos con un multiplicador "de verdad".
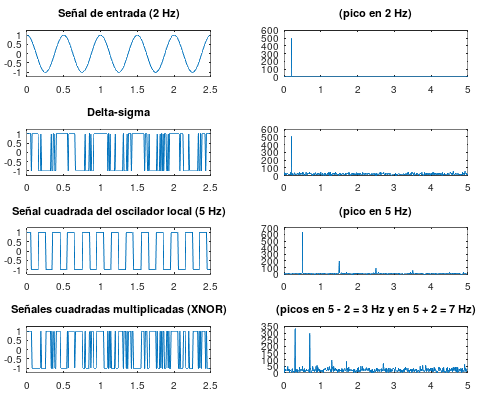
Se ha simulado, por simplicidad, que la señal de entrada (de antena) es de 2 Hz y que la señal del oscilador local es de 5 Hz. La primera columna se corresponde con el dominio del tiempo mientras que la segunda columna se corresponde con el dominio de la frecuencia:
1.- Al principio tenemos una señal senoidal normal de 2 Hz.
2.- A continuación calculamos una señal delta-sigma a partir de esa señal de entrada de 2 Hz (en la Wikipedia se explican ampliamente los principios de esta modulación pero podemos quedarnos con esta pequeña gráfica que resume en qué consiste esta modulación, que es lo que hace nuestro ADC).
3.- Por otro lado tenemos el oscilador local de onda cuadrada que, en este ejemplo, lo hemos puesto a 5 Hz.
4.- Multiplicamos ambas señales (XNOR) y el resultado, como se puede comprobar en las gráficas, es el deseado: se generan dos frecuencias, una suma (7 Hz) y otra resta (3 Hz), de las frecuencias de las dos señales de entrada (antena y oscilador local).
Implementación en la FPGA
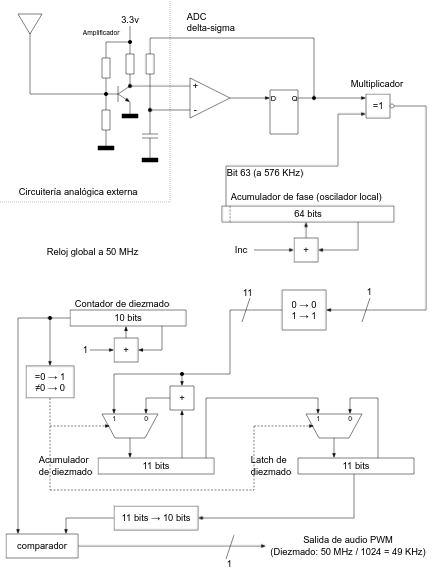
Para el ADC delta-sigma se sigue una configuración estándar como la descrita en esta publicación anterior y se calcula el valor de la resistencia y del condensador de integración en función de la frecuencia de reloj de la FPGA (50 MHz) usando el criterio publicado por Lattice Semiconductor:
$$200 < R \times C \times f_{clk} < 1000$$
Para nuestro caso particular usamos los valores C = 10 nF y R = 1 K. Por otro lado tenemos el acumulador de fase que hace las veces de oscilador local y cuya constante de incremento se calcula a partir de la frecuencia queremos sintonizar (nótese que, como usamos la técnica Zero-IF, la frecuencia del oscilador local deberá ser exactamente la misma que la de la emisora que queremos sintonizar). Si queremos sintonizar 576 KHz (en mi caso es la frecuencia a la que emite Radio Nacional de España en Las Palmas de Gran Canaria) calcularemos la constante de incremento del acumulador de fase de la siguiente manera:
$$Inc = {576000 \over 50000000} \times 2^{64} = 212506491729134048$$
De esta manera en el bit 63 (el más significativo) del acumulador de fase tendremos una onda cuadrada con una frecuencia de 576 KHz. Como se comentó con anterioridad, la multiplicación la implementamos mediante una simple puerta XNOR entre el bit 63 del acumulador de fase (oscilador local de onda cuadrada) y el bit proveniente del ADC delta-sigma.
A la salida de la puerta XNOR (nuestro particular multiplicador) convertimos la señal de 1 bit en una señal de 11 bits apta para ser acumulada en el registro de diezmado (en algunos textos técnicos se hace referencia al "diezmado" como "decimación", a mi me gusta más el término "diezmado", ya que es la traducción más correcta del término "decimation" y creo que expresa mejor su cometido).
Lo que hace el acumulador de diezmado es ir sumando las muestras que llegan del multiplicador (la puerta XNOR) y cuando ha hecho 1024 sumas (o, lo que es lo mismo, cuando el contador de diezmado se desborda), se pasa el valor de la cuenta al latch de diezmado y se inicia el acumulador de diezmado de nuevo. ¿Cual es el resultado de esto? Lo que estamos haciendo es un "diezmado en tiempo" y convertir una señal con una frecuencia de muestreo de 50 MHz (los 0s y 1s que salen del multiplicador) en otra señal con una frecuencia de muestreo de ${50000000 \over {2^{10}}} = {50000000 \over 1024} = 48828.125 \simeq 49 \: KHz$. Con este diezmado en tiempo matamos dos pájaros de un tiro:
1.- Por un lado, hacemos un filtrado paso-bajo, ya que estamos "promediando" y generamos una muestra de salida por cada 1024 muestras de entrada.
2.- Por otro lado, ajustamos la frecuencia de muestreo de la señal a un valor aceptable para ser procesado por circuitos de audio.
La salida del latch de diezmado ya es apta para convertirla a PWM y sacarla por un altavoz.
library ieee; use ieee.std_logic_1164.all; use ieee.numeric_std.all; entity CycloneIIAMReceiver is port ( ClkIn : in std_logic; -- 50 MHz AntennaIn : in std_logic; DeltaSigmaOut : out std_logic; SpeakerOut : out std_logic ); end entity; architecture A of CycloneIIAMReceiver is -- 1-bit ADC signal DeltaSigmaADCD : std_logic; signal DeltaSigmaADCQ : std_logic; -- COPE AM Las Palmas: 837 KHz -- (837000 / 50000000) * (2 ^ 64) = 308798495793897920 (64 bit) -- upper 32 bit: 71897752 -- lower 32 bit: 2297979328 ----constant UPPER_LOCAL_OSC_INC : integer := 71897752; ----constant LOWER_LOCAL_OSC_INC : integer := 2297979328; -- RNE AM Las Palmas: 576 KHz -- (576000 / 50000000) * (2 ^ 64) = 212506491729134048 (64 bit) -- upper 32 bit: 49478023 -- lower 32 bit: 1073398240 constant UPPER_LOCAL_OSC_INC : integer := 49478023; constant LOWER_LOCAL_OSC_INC : integer := 1073398240; constant LOCAL_OSC_INC : std_logic_vector(63 downto 0) := std_logic_vector(to_unsigned(UPPER_LOCAL_OSC_INC, 32)) & std_logic_vector(to_unsigned(LOWER_LOCAL_OSC_INC, 32)); signal LocalOscAccD : std_logic_vector(63 downto 0); signal LocalOscAccQ : std_logic_vector(63 downto 0); signal LocalOscOut : std_logic; -- mixer signal MixerOut : std_logic; signal NumericMixerOut : std_logic_vector(10 downto 0); -- decimator (factor = 1024 = 2^10, so pass from 50 MHz to 48.8 KHz (50000000 / 1024) signal DecimatorCounterD : std_logic_vector(9 downto 0); signal DecimatorCounterQ : std_logic_vector(9 downto 0); signal DecimatorAccD : std_logic_vector(10 downto 0); signal DecimatorAccQ : std_logic_vector(10 downto 0); signal DecimatorLatchD : std_logic_vector(10 downto 0); signal DecimatorLatchQ : std_logic_vector(10 downto 0); signal DemodulatedOutput : std_logic_vector(9 downto 0); begin -- delta-sigma ADC for input process (ClkIn) begin if (ClkIn'event and (ClkIn = '1')) then DeltaSigmaADCQ <= DeltaSigmaADCD; end if; end process; DeltaSigmaADCD <= AntennaIn; DeltaSigmaOut <= DeltaSigmaADCQ; -- local oscillator process (ClkIn) begin if (ClkIn'event and (ClkIn = '1')) then LocalOscAccQ <= LocalOscAccD; end if; end process; LocalOscAccD <= std_logic_vector(unsigned(LocalOscAccQ) + unsigned(LOCAL_OSC_INC)); LocalOscOut <= LocalOscAccQ(63); -- mixer (multiplier) MixerOut <= LocalOscOut xnor DeltaSigmaADCQ; NumericMixerOut <= std_logic_vector(to_unsigned(1, 11)) when (MixerOut = '1') else std_logic_vector(to_unsigned(0, 11)); -- decimator process (ClkIn) begin if (ClkIn'event and (ClkIn = '1')) then DecimatorCounterQ <= DecimatorCounterD; end if; end process; DecimatorCounterD <= std_logic_vector(unsigned(DecimatorCounterQ) + to_unsigned(1, 10)); process (ClkIn) begin if (ClkIn'event and (ClkIn = '1')) then DecimatorAccQ <= DecimatorAccD; end if; end process; DecimatorAccD <= NumericMixerOut when (unsigned(DecimatorCounterQ) = 0) else std_logic_vector(unsigned(DecimatorAccQ) + unsigned(NumericMixerOut)); process (ClkIn) begin if (ClkIn'event and (ClkIn = '1')) then DecimatorLatchQ <= DecimatorLatchD; end if; end process; DecimatorLatchD <= DecimatorAccQ when (unsigned(DecimatorCounterQ) = 0) else DecimatorLatchQ; DemodulatedOutput <= DecimatorLatchQ(10 downto 1); -- PWM for speaker output SpeakerOut <= '1' when (unsigned(DecimatorCounterQ) > unsigned(DemodulatedOutput)) else '0'; end architecture;
Salida PWM
La parte de la salida PWM de la FPGA lo que hace es convertir la señal del latch de diezmado en un tren de pulsos PWM que se conecta directamente a un amplificador de audio externo. El bit de salida PWM se calcula comparando el valor del latch de diezmado con el contador de diezmado, lo que provoca que la anchura de los pulsos de salida (un único bit que va al amplificador) sea proporcional al valor del latch de diezmado. Este bit (modulado en PWM) puede atacar directamente a la entrada de cualquier amplificador de audio.
Esquema eléctrico final
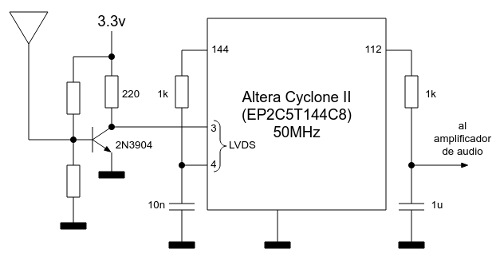
Resultados
Los resultados distan mucho de considerarse de calidad, el ruido en la recepción es alto (sólo a mi se me ocurre montar un circuito de radio en una protoboard...), pero "se entiende" más o menos lo que dice :-). El amplificador de antena ha sido la parte que, de lejos, más trabajo me ha dado, ya que tengo que reconocer que mi fuerte no es la electrónica analógica y menos a estas frecuencias de trabajo.
El código fuente puede descargarse de la sección soft.
[ 2 comentarios ] ( 26583 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 2838 )
( 3 / 2838 )
 Calendario
Calendario




