Esquema
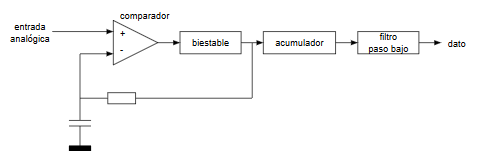
Como se puede apreciar la parte analógica del conversor se reduce a un comparador, una resistencia y un condensador. En la "zona digital" tenemos todo el meollo: un biestable, un acumulador y un filtro paso bajo. Veamos el funcionamiento con una traza sencilla.
Funcionamiento
Asumamos que empezamos con la salida que va al filtro RC a 0 y el condensador totalmente descargado y que en la entrada analógica tenemos un voltaje entre 0 y Vcc (3.3 voltios) que llamaremos $V_{in}$. En estas condiciones iniciales, como $V_{in} > 0$, el comparador emite 3.3 voltios (un 1 lógico) y por tanto, en el siguiente ciclo de reloj, el biestable carga ese 1 en su salida Q.
Tras esta primera carga la salida que va conectada al filtro RC (la Q del biestable) se pone a 1, lo que significa que el condensador empieza a cargarse a través de R. Para cuando llegue el siguiente ciclo de reloj lo más probable es que la carga del condensador aún sea muy baja y el comparador siga emitiendo a su salida un 1 (su entrada + tiene un voltaje aún mayor que su entrada -). Tendremos, por tanto que el biestable seguirá emitiendo 1s hasta que el voltaje en la entrada - del comparador sea superior a $V_{in}$, en el momento que ocurra eso la salida del comparador será de 0 voltios (un 0 lógico). El biestable en el siguiente ciclo de reloj cargará ese 0 en su Q y el condensador empezará ahora a descargarse a través de la R.
Como se puede apreciar, el sistema en lazo cerrado lo que hace es, mediante 0s y 1s tratar de hacer que el voltaje en la entrada - del comparador (el voltaje en el condensador) "siga" al voltaje de entrada $V_{in}$ y esto, en la práctica, significa que a la salida del biestable lo que tenemos es una especie de señal PWM cuyo ciclo de trabajo será proporcional al voltaje $V_{in}$:
1.- Cuanto mayor es el valor de $V_{in}$, mayor cantidad de 1s emite el biestable para tratar de "alcanzar" $V_{in}$.
2.- Cuanto menor es el valor de $V_{in}$, mayor es la cantidad de 0s que emite el biestable para tratar de "alcanzar" $V_{in}$.
3.- Se puede ver, además, que para un valor próximo a ${Vcc \over 2}$ el biestable emitirá aproximadamente la misma cantidad de 0s que de 1s por unidad de tiempo.
Ahora supongamos que pasamos la salida del biestable por un circuito combinacional que ante un 0 en la entrada emite un -1 en un bus de N bits y ante un 1 en la entrada emite un +1 en esa misma salida de N bits. Si durante $2^{N-1}$ ciclos de reloj vamos sumando en un acumulador con signo los valores +1 y -1 que van saliendo de este circuito combinacional tendremos lo siguiente:
1.- Para valores altos de $V_{in}$, que generan muchos más 1s que 0s en la salida del biestable, tendremos que el acumulador cada $2^{N-1}$ ciclos de reloj tendrá un valor próximo a $2^{N-1}$.
2.- Para valores bajos de $V_{in}$, que generan muchos más 0s que 1s en la salida del biestable, tendremos que el acumulador, cada $2^{N-1}$ ciclos de reloj, tendrá un valor próximo a $-2^{N-1}$.
3.- Para valores próximos a ${Vcc \over 2}$, que generan una cantidad muy similar de 0s y de 1s por unidad de tiempo, tendremos que el acumulador, cada $2^{N-1}$ ciclos de reloj, tendrá un valor próximo a 0.
Si cada $2^{N-1}$ ciclos de reloj cargamos el valor de este acumulador sobre un registro (que podemos llamar de salida), justo antes de poner de nuevo el acumulador a 0 (y volver a acumular los +1 y -1 que llegan del biestable), tenemos que este registro de salida será el resultado de la conversión analógico-digital del voltaje de entrada $V_{in}$ en N bits, que era nuestro objetivo. En la implementación recomendada se introduce una tercera etapa que realiza un sobremuestreo adicional para suavizar la señal (actúa como filtro paso bajo) pero que no se ha implementado en este caso por simplicidad.
Otra característica importante en este tipo de conversores es que la resolución en bits del conversor viene determinada por N (la anchura en bits del acumulador y del filtro paso bajo), que es un parámetro relativamente sencillo de cambiar, y que no requiere cambios en la electrónica externa.
Implementación
A continuación puede verse un esquema detallado de lo que sería la implementación en una FPGA o en un CPLD del conversor descrito:
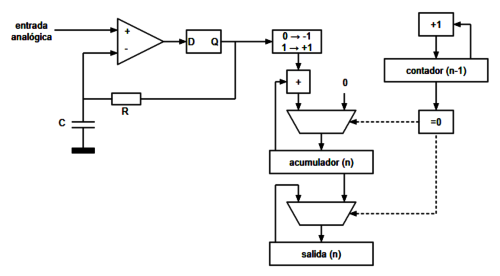
Cada vez que el contador pasa por 0 hace que en acumulador se cargue en el registro de salida y al mismo tiempo se reinicie con el valor 0. Los valores de la resistencia R y del condensador C deben ser elegidos acorde a la frecuencia de reloj del sistema. Por ejemplo, Lattice Semiconductor recomienda que la constante de tiempo del filtro $t = R \times C$ cumpla que $200 < t \times f_{clk} < 1000$. En este caso concreto se ha hecho una implementación sobre un CPLD de Altera (Intel) que va a 50 MHz y se han elegido los valores de C = 1.5 nF y R = 10 K, que cumplen dicha desigualdad.
library ieee; use ieee.std_logic_1164.all; use ieee.numeric_std.all; entity DeltaSigmaADC is port ( Reset : in std_logic; Clk : in std_logic; DataOut : out std_logic_vector(7 downto 0); ComparatorIn : in std_logic; RCChargeOut : out std_logic ); end entity; architecture Architecture1 of DeltaSigmaADC is signal DBus : std_logic; signal QBus : std_logic; signal FollowerOut : std_logic_vector(15 downto 0); signal CounterDBus : std_logic_vector(14 downto 0); signal CounterQBus : std_logic_vector(14 downto 0); signal IntegratorDBus : std_logic_vector(15 downto 0); signal IntegratorQBus : std_logic_vector(15 downto 0); signal LatchDBus : std_logic_vector(15 downto 0); signal LatchQBus : std_logic_vector(15 downto 0); begin -- biestable de seguimiento de voltaje process (Clk) begin if (Clk'event and (Clk = '1')) then QBus <= DBus; end if; end process; DBus <= ComparatorIn; RCChargeOut <= QBus; FollowerOut <= std_logic_vector(to_signed(-1, 16)) when (QBus = '0') else std_logic_vector(to_signed(1, 16)); -- contador process (Clk) begin if (Clk'event and (Clk = '1')) then CounterQBus <= CounterDBus; end if; end process; CounterDBus <= std_logic_vector(to_signed(0, 15)) when (Reset = '1') else std_logic_vector(signed(CounterQBus) + 1); -- integrador process (Clk) begin if (Clk'event and (Clk = '1')) then IntegratorQBus <= IntegratorDBus; end if; end process; IntegratorDBus <= std_logic_vector(to_signed(0, 16)) when (signed(CounterQBus) = 0) else std_logic_vector(signed(FollowerOut) + signed(IntegratorQBus)); -- latch process (Clk) begin if (Clk'event and (Clk = '1')) then LatchQBus <= LatchDBus; end if; end process; LatchDBus <= IntegratorQBus when (signed(CounterQBus) = 0) else LatchQBus; -- salida DataOut <= LatchQBus(15 downto 8); end architecture;

El código fuente está disponible en la sección soft.
[ añadir comentario ] ( 2674 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 5594 )
( 3 / 5594 )La aritmética de punto fijo es un mecanismo muy útil para la implementación de funciones matemáticas en procesadores sin unidad de coma flotante como microcontroladores y procesadores pequeños de 8 o 16 bits. A lo largo de este post se plantea el uso de la sobrecarga de operadores de C++ para facilitar las tareas de programación y mejorar la legibilidad del código cuando se usan tipos de punto fijo.
Introducción
La aritmética de punto fijo permite realizar operaciones con números fraccionarios mediante tipos enteros y operaciones enteras. En anteriores posts de este blog se ha hablado de forma extensa acerca de este tema, por lo que se remite a ellos a la persona interesada. A lo largo de este post usaré siempre valores de punto fijo Q16.16 (32 bits con 16 bits para la parte entera y 16 bits para la parte fraccionaria).
Implementación tradicional mediante macros
Tradicionalmente siempre he implementado la aritmética de punto fijo con un fichero de cabecera en el que defino "fixedpoint_t" como un "int32_t" y unas macros especiales para las operaciones de conversión de entero a punto fijo, de multiplicación y de división (las más "complejas"):
typedef int32_t fixedpoint_ct; #define FP_MUL(x, y) ((int32_t) ((((int64_t) (x)) * ((int64_t) (y))) >> 16)) #define FP_DIV(x, y) ((int32_t) ((((int64_t) (x)) << 16) / ((int64_t) (y)))) #define TO_FP(x) (((int32_t ) (x)) << 16)
Como se puede apreciar, se trata de una implementación extremadamente sencilla y si lo que queremos es escribir una función que calcule:
$$\left({a \times b}\right) + \left({a \over b}\right)$$
Introduciríamos el siguiente código:
fixedpoint_ct fWithMacros(fixedpoint_ct a, fixedpoint_ct b) { return FP_MUL(a, b) + FP_DIV(a, b); }
Y para los valores $a = 4$ y $b = 3$ la invocaríamos de la siguiente forma:
fixedpoint_ct v = fWithMacros(TO_FP(4), TO_FP(3));
Se trata de una implementación perfectamente válida aunque adolece de falta de claridad en el código: hay que leer con cuidado las operaciones aritméticas para no confundirse. Por otro lado es una implementación que tiene la ventaja de que en todo momento está claro que no estamos trabajando con un tipo "trivial".
Implementación basada en sobrecarga de operadores
Buscando un código más legible que el anterior, lo lógico es recurrir a la sobrecarga de operadores de C++. Definimos una clase "fixedpoint_t" en la que metemos un entero de 32 bits y definimos las cuatro operaciones básicas como "operator" dentro de la propia clase:
class fixedpoint_t { public: int32_t v; fixedpoint_t(int32_t x = 0) : v(x << 16) { }; inline fixedpoint_t &operator = (const int32_t &x) { this->v = x << 16; return *this; }; inline fixedpoint_t operator + (const fixedpoint_t &x) { fixedpoint_t ret; ret.v = this->v + x.v; return ret; }; inline fixedpoint_t operator - (const fixedpoint_t &x) { fixedpoint_t ret; ret.v = this->v - x.v; return ret; }; inline fixedpoint_t operator * (const fixedpoint_t &x) { fixedpoint_t ret; ret.v = (((int64_t) this->v) * ((int64_t) x.v)) >> 16; return ret; }; inline fixedpoint_t operator / (const fixedpoint_t &x) { fixedpoint_t ret; ret.v = (((int64_t) this->v) << 16) / ((int64_t) x.v); return ret; }; };
Esta implementación nos permite ahora escribir la misma función de antes de una forma más legible:
fixedpoint_t fWithOperators(fixedpoint_t a, fixedpoint_t b) { return (a * b) + (a / b); }
Y, de la misma manera, también nos permite invocarla de forma más legible:
fixedpoint_t v = fWithOperators(4, 3);
Sin embargo se podría pensar que una implementación así generaría mucho más código que la implementación basada en macros. Hagamos unas pruebas.
Comparativa
Si compilamos con gcc el código de ambas funciones sin opciones de optimización:
g++ -std=c++11 -o fp fp.cc
la diferencia es abismal:
_Z11fWithMacrosii:
push %rbp
mov %rsp,%rbp
push %rbx
mov %edi,-0xc(%rbp)
mov %esi,-0x10(%rbp)
mov -0xc(%rbp),%eax
movslq %eax,%rdx
mov -0x10(%rbp),%eax
cltq
imul %rdx,%rax
sar $0x10,%rax
mov %eax,%ecx
mov -0xc(%rbp),%eax
cltq
shl $0x10,%rax
mov -0x10(%rbp),%edx
movslq %edx,%rbx
cqto
idiv %rbx
add %ecx,%eax
pop %rbx
pop %rbp
retq
_Z14fWithOperators12fixedpoint_tS_:
push %rbp
mov %rsp,%rbp
sub $0x40,%rsp
mov %edi,-0x30(%rbp)
mov %esi,-0x40(%rbp)
lea -0x40(%rbp),%rdx
lea -0x30(%rbp),%rax
mov %rdx,%rsi
mov %rax,%rdi
callq 4009cc <_ZN12fixedpoint_tdvERKS_>
mov %eax,-0x20(%rbp)
lea -0x40(%rbp),%rdx
lea -0x30(%rbp),%rax
mov %rdx,%rsi
mov %rax,%rdi
callq 40098a <_ZN12fixedpoint_tmlERKS_>
mov %eax,-0x10(%rbp)
lea -0x20(%rbp),%rdx
lea -0x10(%rbp),%rax
mov %rdx,%rsi
mov %rax,%rdi
callq 400952 <_ZN12fixedpoint_tplERKS_>
leaveq
retq
El compilador ha hecho caso omiso del "inline" de las funciones miembro de la clase "fixedpoint_t" y las ha implementado como funciones aparte en ensamblador. En este caso la implementación usando macros es más eficiente. Activemos ahora el primer nivel de optimización "-O1":
g++ -std=c++11 -O1 -o fp fp.cc
Voilà, ahora apenas notamos la diferencia en el código generado:
_Z11fWithMacrosii:
movslq %edi,%rax
movslq %esi,%rsi
mov %rax,%rcx
imul %rsi,%rcx
sar $0x10,%rcx
shl $0x10,%rax
cqto
idiv %rsi
add %ecx,%eax
retq
_Z14fWithOperators12fixedpoint_tS_:
movslq %edi,%rdi
movslq %esi,%rsi
mov %rdi,%rax
shl $0x10,%rax
cqto
idiv %rsi
imul %rdi,%rsi
sar $0x10,%rsi
add %esi,%eax
retq
La implementación utilizando la clase "fixedpoint_t" con los operadores sobrecargados genera un código igual de eficiente que la implementación basada en macros.
Como conclusión podemos sacar que no es necesario sacrificar legibilidad en aras de la velocidad de ejecución, siempre y cuando usemos correctamente los elementos del lenguaje y compilemos usando las opciones de optimización adecuadas.
El código fuente puede descargarse de la sección soft.
[ añadir comentario ] ( 4323 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 12853 )
( 3 / 12853 )A la hora de controlador un display LCD mediante el conocido adaptador I2C la gran mayoría de ejemplos disponibles por ahí implementan los estados de espera necesarios mediante retardos explícitos ("delays"). Dichas implementaciones están bien como prueba de concepto, pero no son deseables en entornos multitarea donde no podemos desperdiciar ciclos sólo esperando. En entornos reales se precisa de implementaciones no bloqueantes que hagan uso de timers e interrupciones.
El circuito
La interfaz de un display LCD estándar de caracteres es una interfaz paralelo de 8 bits, con 3 líneas de control adicionales (RS, EN y RW). Del bus paralelo de 8 bits pueden usarse sólo los 4 bits más significativos enviando de forma adecuada los comandos. Los circuitos de conversión a I2C que se venden habitualmente por AliExpress, Ebay y demás están basados en el conversor I2C/paralelo de 8 bits PCF8574 de Texas Instruments: del bus paralelo de dicho conversor se sacan los 4 bits más significativos para el bus paralelo del LCD y las tres señales de control para RS, EN y RW.
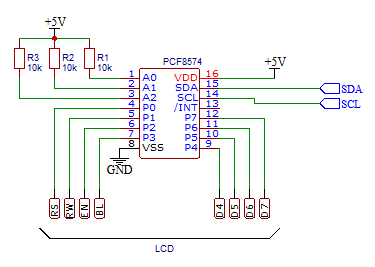
La configuración habitual en este tipo de módulos es esta:
| PCF8574 | bit 7 | bit 6 | bit 5 | bit 4 | bit 3 | bit 2 | bit 1 | bit 0 |
| LCD | D7 | D6 | D5 | D4 | BL | EN | RW | RS |
En la tabla se puede apreciar una cuarta señal de control etiquetada como BL (backlight) que controla el encendido del led de la luz trasera. Dicho led no forma parte de la circuitería estándar del display y ha sido introducido en versiones más recientes.
El problema
Los displays baratos de caracteres LCD que se encuentran en el mercado están basados en en un chip de Hitachi que no se caracteriza precisamente por su velocidad (probablemente debe ser uno de los chips más rentabilizados de toda la historia de Hitachi) y normalmente cada acceso debe estar seguido por una espera de uno a varios microsegundos, dependiendo del acceso realizado. A continuación puede verse la tabla de comandos de referencia del display, nótese la columna de la derecha ("Execution Time"):
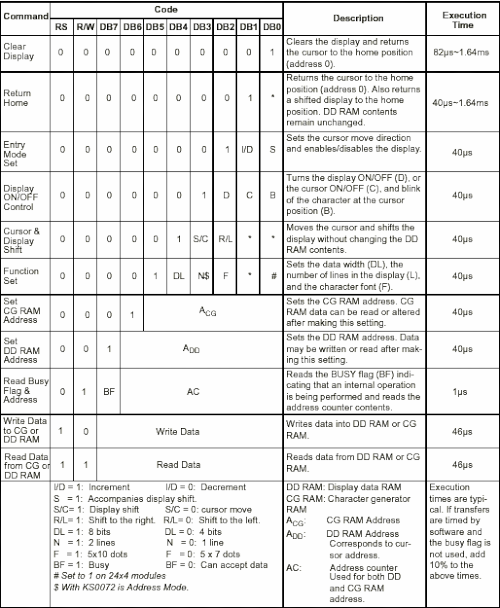
(imagen extraida de https://learningmsp430.wordpress.com/2013/11/13/16x2-lcd-interfacing-in-8bit-mode/)
Cuando uno realiza una búsqueda en internet sobre códigos de ejemplo para control de displays LCD, la gran mayoría de los mismos (no digo todos porque considero que no los he visto todos, pero al menos todos los que yo he visto), implementan las esperas mediante retardos utilizando funciones "delay" o similares. Esta forma de implementación, aunque resulta simple, supone un desperdicio de ciclos e impide que el microcontrolador realice otras tareas de forma concurrente.
La solución no bloqueante
La solución ideal pasaría por una implementación basada en colas y en interrupciones. En este caso se ha implementado una máquina de estados que controla el flujo de datos I2C, el troceado de los bytes en dos nibbles y las esperas que hay que realizar entre un envío y el siguiente. Grosso modo, la solución sería la siguiente:
- Cada vez que se quiere escribir en el display, lo que se hace es escribir lo que se quiere mandar al display en una cola de datos, por lo que la función encargada de escribir regresa inmediatamente (no es bloqueante).
- El systick del microcontrolador cuando detecta que hay algún dato en la cola de datos inicia una máquina de estados que se encarga de trocear en byte en dos nibbles y enviarlos en tiempos diferentes, así hasta que la cola de datos quede vacía, en cuyo momento la máquina de estados pasa a modo "IDLE" y queda a la espera que de haya más datos en la cola.
- La capa I2C también está implementada como una cola de bytes de tal manera que si la capa LCD quiere escribir N bytes seguidos por I2C, los escribe de forma no bloqueante en la cola I2C (la función de escritura I2C también regresa inmediatamente) y se va vaciando a medida que la interrupción de callback de transmisión es llamada por el microcontrolador.
A continuación puede verse cómo ha quedado la máquina de estados del controlador LCD:
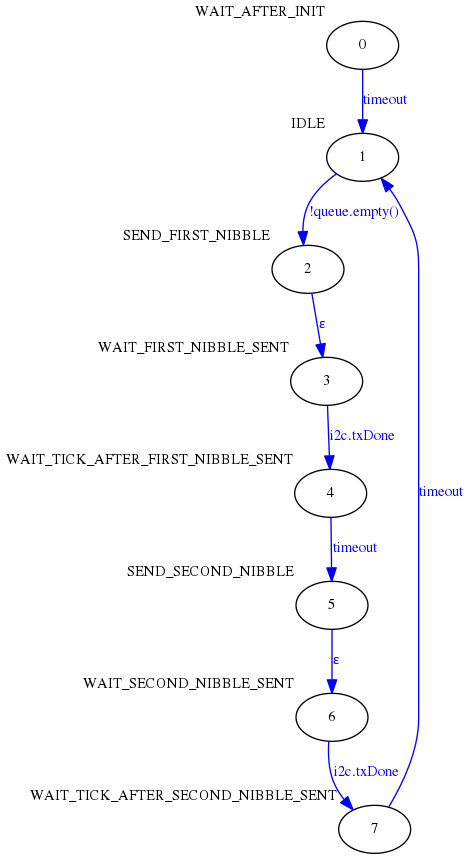
El código no queda tan sencillo a simple vista pero se trata, sin duda, de una implementación más eficiente.
#include "LCD.H" using namespace avelino; using namespace std; void LCD::init(uint8_t address) { this->address = address; this->timerCounter = 5; this->status = LCD::Status::WAIT_AFTER_INIT; this->queue.push(LCD::QueueItem(0x33, LCD::IsCommand::YES)); this->queue.push(LCD::QueueItem(0x32, LCD::IsCommand::YES)); this->queue.push(LCD::QueueItem(0x28, LCD::IsCommand::YES)); this->queue.push(LCD::QueueItem(0x08, LCD::IsCommand::YES)); this->queue.push(LCD::QueueItem(0x01, LCD::IsCommand::YES)); this->queue.push(LCD::QueueItem(0x06, LCD::IsCommand::YES)); this->queue.push(LCD::QueueItem(0x0C, LCD::IsCommand::YES)); } void LCD::tick() { Status localStatus = this->status; do { this->status = localStatus; if (localStatus == LCD::Status::WAIT_AFTER_INIT) { if (this->timerCounter > 0) this->timerCounter--; else localStatus = LCD::Status::IDLE; } else if (localStatus == LCD::Status::IDLE) { if (!this->queue.empty()) { I2CManager::deviceAddress = this->address << 1; localStatus = LCD::Status::SEND_FIRST_NIBBLE; } } else if (localStatus == LCD::Status::SEND_FIRST_NIBBLE) { uint8_t byte = this->queue.head().byte; LCD::IsCommand isCommand = this->queue.head().isCommand; I2CManager::txQueue.push((byte & 0xF0) | ((isCommand == LCD::IsCommand::YES) ? LCD::RS_0 : LCD::RS_1) | LCD::RW_0 | LCD::EN_1 | LCD::BL_1); I2CManager::txQueue.push((byte & 0xF0) | ((isCommand == LCD::IsCommand::YES) ? LCD::RS_0 : LCD::RS_1) | LCD::RW_0 | LCD::EN_0 | LCD::BL_1); I2CManager::send(); localStatus = LCD::Status::WAIT_FIRST_NIBBLE_SENT; } else if (localStatus == LCD::Status::WAIT_FIRST_NIBBLE_SENT) { if (I2CManager::txDone) { this->timerCounter = 1; localStatus = LCD::Status::WAIT_TICK_AFTER_FIRST_NIBBLE_SENT; } } else if (localStatus == LCD::Status::WAIT_TICK_AFTER_FIRST_NIBBLE_SENT) { if (this->timerCounter > 0) this->timerCounter--; else localStatus = LCD::Status::SEND_SECOND_NIBBLE; } else if (localStatus == LCD::Status::SEND_SECOND_NIBBLE) { uint8_t byte = this->queue.head().byte << 4; LCD::IsCommand isCommand = this->queue.head().isCommand; this->queue.pop(); I2CManager::txQueue.push((byte & 0xF0) | ((isCommand == LCD::IsCommand::YES) ? LCD::RS_0 : LCD::RS_1) | LCD::RW_0 | LCD::EN_1 | LCD::BL_1); I2CManager::txQueue.push((byte & 0xF0) | ((isCommand == LCD::IsCommand::YES) ? LCD::RS_0 : LCD::RS_1) | LCD::RW_0 | LCD::EN_0 | LCD::BL_1); I2CManager::send(); localStatus = LCD::Status::WAIT_SECOND_NIBBLE_SENT; } else if (localStatus == LCD::Status::WAIT_SECOND_NIBBLE_SENT) { if (I2CManager::txDone) { this->timerCounter = 1; localStatus = LCD::Status::WAIT_TICK_AFTER_SECOND_NIBBLE_SENT; } } else if (localStatus == LCD::Status::WAIT_TICK_AFTER_SECOND_NIBBLE_SENT) { if (this->timerCounter > 0) this->timerCounter--; else localStatus = LCD::Status::IDLE; } } while (localStatus != this->status); } void LCD::write(const char *s, int16_t size, LCD::IsCommand isCommand) { while ((*s != 0) && ((size < 0) || (size > 0))) { this->queue.push(QueueItem(*s, isCommand)); s++; if (size > 0) size--; } }
La función miembro "tick" es invocada desde la interrupción systick del microcontrolador en "main.cc":
LCD lcd; void systick() __attribute__ ((section(".systick"))); void systick() { lcd.tick(); }
Nótese que las colas (tanto la cola I2C como la cola LCD) están implementadas usando colas circulares estáticas a través de una plantilla ("StaticQueue.H").
#ifndef __STATICQUEUE_H__ #define __STATICQUEUE_H__ #include <stdint.h> extern "C++" { namespace avelino { using namespace std; template <typename T, int32_t N> class StaticQueue { public: T data[N]; int32_t headIndex; int32_t tailIndex; void push(const T &v); const T &head() { return this->data[this->headIndex]; }; void pop(); bool empty() { return (this->headIndex == this->tailIndex); }; StaticQueue() : headIndex(0), tailIndex(0) { }; }; template <typename T, int32_t N> void StaticQueue<T, N>::push(const T &v) { this->data[this->tailIndex] = v; this->tailIndex++; if (this->tailIndex == N) this->tailIndex = 0; } template <typename T, int32_t N> void StaticQueue<T, N>::pop() { this->headIndex++; if (this->headIndex == N) this->headIndex = 0; } } } #endif // __STATICQUEUE_H__
Se ha utilizado en varios sitios el "enum class", que permite trabajar con enumerados fuertemente tipados (introducido en el estándar C++11).
En la sección soft puede descargarse todo el código fuente.
[ añadir comentario ] ( 2758 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 13115 )
( 3 / 13115 )En esta primera entrega del podcast he entrevistado a Bartolomé Almeida, un ingeniero de telecomunicaciones que se ha especializado en el estándar LoRa. Nos ha hablado de las diferentes aplicaciones, módulos y librerías disponibles para empezar en el mundo de las comunicaciones a larga distancia usando este estándar.
El episodio 1 está disponible aquí.
La música utilizada es de The Underscore Orkestra. Licencia Creative Commons con atribución.
[ añadir comentario ] ( 2244 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 13584 )
( 3 / 13584 )Me he estrenado en esto de los podcasts y he decidido empezar a hacer un podcast en español sobre microcontroladores, sistemas embebidos y desarrollo de sistemas digitales.

El episodio 0 está disponible aquí.
La música utilizada es de The Underscore Orkestra. Licencia Creative Commons con atribución.
[ 1 comentario ] ( 2271 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 13920 )
( 3 / 13920 )
 Calendario
Calendario




