El episodio 1 está disponible aquí.
La música utilizada es de The Underscore Orkestra. Licencia Creative Commons con atribución.
[ añadir comentario ] ( 2197 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 13491 )
( 3 / 13491 )Me he estrenado en esto de los podcasts y he decidido empezar a hacer un podcast en español sobre microcontroladores, sistemas embebidos y desarrollo de sistemas digitales.

El episodio 0 está disponible aquí.
La música utilizada es de The Underscore Orkestra. Licencia Creative Commons con atribución.
[ 1 comentario ] ( 2214 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 13846 )
( 3 / 13846 )Un año más, decorando el belén con nuevos inventos. En esta ocasión he vuelto a los orígenes y he implementado una luz, pero esta vez una luz especial que simule un fuego encendido utilizando un CPLD.
Introducción
A la hora de simular el crepitar de una llamas se ha optado por hacer que un led varíe de luminosidad de forma aleatoria varias veces por segundo.
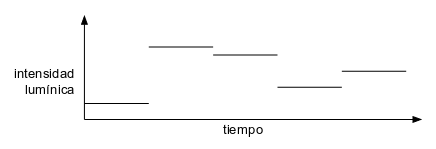
Con una luz que varíe su intensidad lumínica varias veces por segundo (entre 5 y 6 veces por segundo, por ejemplo) más una buena escenografía (color de la luz, decorados, etc.) se consigue un razonable efecto de fuego encendido.
Diseño técnico
Como vamos a hacer el diseño utilizando un circuito totalmente digital, la intensidad lumínica se modulará utilizando una señal cuadrada modulada en anchura (PWM). Cuanto mayor sea el semiciclo a 1 y menor el semiciclo a 0 más brillará el led y a la inversa: cuanto mayor sea el semiciclo a 0 y menor el semiciclo a 1 menos brillará.
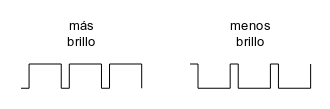
Si hacemos que la frecuencia sea lo suficientemente alta no se apreciará ningún tipo de parpadeo y la luz se percibirá como que brilla de forma continuada pero con diferente intensidad. El CPLD utilizado tiene conectado un reloj a 50 MHz, por tanto usando un contador de 10 bits estándar conseguiremos un desbordamiento a una frecuencia de
$${50000000 \over {2^{10}}} = 48828.125 Hz$$
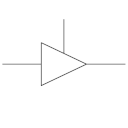
Si el valor de este contador lo comparamos con un valor determinado, el resultado de esta comparación será la salida PWM que necesitamos para el led de nuestra fogata:
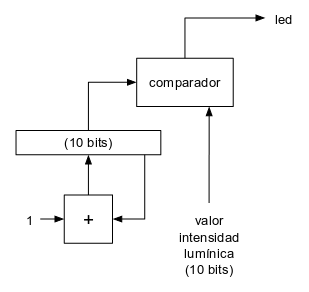
El valor de intensidad lo generaremos mediante un LFSR maximal de 10 bits. Dicho LFSR ha sido utilizado en otros montajes anteriores:
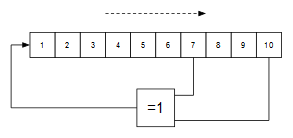
Genera una secuencia maximal de 1023 valores pseudoaleatorios (el valor 0 no aparece en la secuencia) que se puede usar como valor de intensidad lumínica:
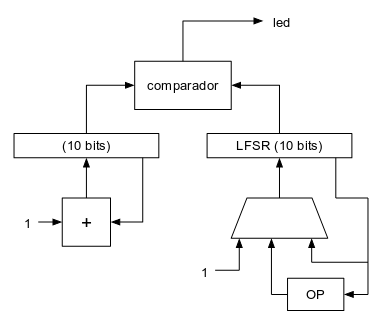
En este circuito el bloque combinacional "OP" es el que implementa el polinomio maximal de 10 bits. A continuación sólo falta implementar la temporización. Como queremos el que valor de intensidad lumínica cambie unas 5 ó 6 veces por segundo, bastará con poner un contador estándar de:
$$\lceil log_2\left({50000000 \over 6}\right) \rceil = 23 bits$$
Con un contador de 23 bits a 50 MHz tendremos una frecuencia de desbordamiento de casi 6 veces por segundo:
$${50000000 \over {2^{23}}} = 5.96 Hz$$
A continuación puede verse cómo quedaría el diagrama completo:
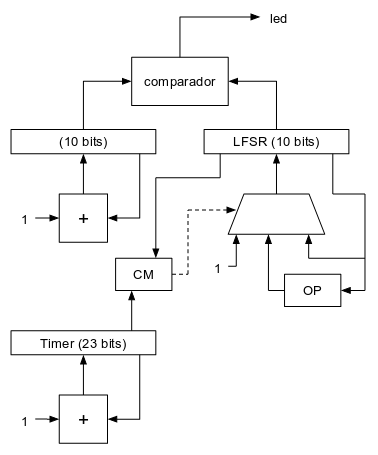
El bloque combinacional "CM" (Control del Multiplexor) se encarga de controlar la selección del multiplexor del LFSR en función del timer contador de 23 bits y del valor del propio LFSR. La tabla de verdad de este bloque sería la siguiente:
| Entradas | Salidas | |
|---|---|---|
| Timer == 0 | LFSR == 0 | MUX |
| X | 1 | "1" |
| 1 | 0 | Salida de OP |
| 0 | 0 | Salida del LFSR |
Cuando el valor del LFSR es 0, lo que hace es seleccionarla entrada "1" del multiplexor para que el LFSR se cargue con un valor distinto de cero (el 1) y poder así arrancar la generación de números aleatorios. Cuando el timer (contador de 23 bits) se desborda (pasa por cero) el LFSR se carga con el siguiente valor de la secuencia de números pseudoaleatorios y el resto del tiempo (valor del contador de 23 bits diferente de 0) el registro LFSR permanece inalterado.
Como se puede apreciar, se ha prescindido de circuitería de reset. Teniendo en cuenta que el objetivo es minimizar la circuitería y que los fabricantes siempre te garantizan que en el arranque, todos los biestables están a 0, se puede "abusar" de esta característica y ahorrar así parte de la circuitería de reset.
Posibles mejoras
Como se puede apreciar, del contador que hace de timer (el de 23 bits) sólo nos interesa cuando pasa por un valor concreto (el 0), no es como el contador que se utiliza para comparar con el LFSR y generar la señal PWM. Teniendo esto presente, dicho contador de 23 bits podría implementarse utilizando también un LFSR maximal de 23 bits: en lugar de un sumador, se puede implementar un bloque combinacionar consistente tan solo en una única puerta xor (ver polinomio a aplicar aquí), lo que supone un ahorro considerable en circuitería.
Hay que tener presente que los LFSRs no pasan nunca por cero, por lo que habría que elegir cualquier otro valor (cualquiera) como valor de "desbordamiento" (el valor 1, por ejemplo).
Implementación
A continuación puede verse la implementación de este diseño en VHDL.
library ieee; use ieee.std_logic_1164.all; use ieee.numeric_std.all; entity ChristmasFire is port ( Clk : in std_logic; Led : out std_logic ); end entity; architecture RTL of ChristmasFire is signal CounterDBus : std_logic_vector(9 downto 0); signal CounterQBus : std_logic_vector(9 downto 0); signal LFSRDBus : std_logic_vector(9 downto 0); signal LFSRQBus : std_logic_vector(9 downto 0); signal TimerDBus : std_logic_vector(22 downto 0); signal TimerQBus : std_logic_vector(22 downto 0); signal TimerOverflow : std_logic; begin -- pwm counter process (Clk) begin if (Clk'event and (Clk = '1')) then CounterQBus <= CounterDBus; end if; end process; CounterDBus <= std_logic_vector(signed(CounterQBus) + to_signed(1, 10)); -- lfsr process (Clk) begin if (Clk'event and (Clk = '1')) then LFSRQBus <= LFSRDBus; end if; end process; LFSRDBus <= std_logic_vector(to_signed(1, 10)) when (signed(LFSRQBus) = to_signed(0, 10)) else ((LFSRQBus(3) xor LFSRQBus(0)) & LFSRQBus(9 downto 1)) when (TimerOverflow = '1') else LFSRQBus; -- timer process (Clk) begin if (Clk'event and (Clk = '1')) then TimerQBus <= TimerDBus; end if; end process; TimerDBus <= std_logic_vector(signed(TimerQBus) + to_signed(1, 23)); TimerOverflow <= '1' when (signed(TimerQBus) = to_signed(0, 23)) else '0'; -- output Led <= '1' when (signed(CounterQBus) > signed(LFSRQBus)) else '0'; end architecture;
Se trata de un único fichero que puede descargarse desde la sección soft.
¡Feliz Navidad a todos!
[ añadir comentario ] ( 2160 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 11235 )
( 3 / 11235 )Partiendo del montaje realizado en el post anterior, se han realizado varias modificaciones y mejoras. El parser MIDI de esta segunda iteración genera ahora 3 señales de control, de 7 bits cada una, que se utilizan para controlar la frecuencia de corte, la resonancia y la ganancia de la entrada de un filtro paso bajo de segundo orden:
Este sería el diagrama de bloques de esta segunda iteración:
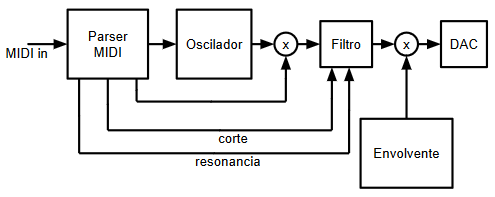
Parser MIDI mejorado
En la versión iniciar el parser MIDI no se tuvieron en cuenta algunas características "raras" que se dan el algunos teclados controladores y al mismo tiempo se asumía que un "note off" posterior a un "note on" siempre era de la misma tecla, lo cual es demasiado suponer, sobre todo cuando quien toca es un humano. Cuando un humano toca una secuencia de notas en un teclado (por ejemplo: La, Mi, Do) uno puede pensar que los mensaje que manda el teclado controlador son los siguientes:
noteOn(La), noteOff(La), noteOn(Mi), noteOff(Mi), noteOn(Do), noteOff(Do)
Sin embargo lo cierto es que a veces un humano pulsa la siguiente tecla al mismo tiempo o antes de soltar la anterior:
noteOn(La), noteOn(Mi), noteOff(La), noteOff(Mi), noteOn(Do), noteOff(Do)
Con la anterior versión del parser, que asumía que un noteOff se correspondía siempre con el noteOn inmediatamente anterior, lo que ocurría era que cuando al sinte le llegaba el noteOff(La) callaba la nota Mi disparada justo antes porque asumía que ese noteOff se correspondía con dicha nota Mi. En la nueva versión del parse este noteOff(Mi) es ignorado por la máquina de estados por lo que la respuesta del sintetizador es más natural.
Para mejorar el comportamiento y la funcionalidad del parser MIDI se ha optado por un diseño basado en máquinas de estado en serie y en paralelo en lugar de una única máquina de estados grande. El parser MIDI se ha divido en dos etapas (Stage1 y Stage2), la primera etapa genera señales "KeyOn" y "KeyOff" limpias por cables separados y además implementa en paralelo una máquina de estados aparte para procesar los mensajes de "Control Change". En la segunda etapa se implementa la lógica anteriormente descrita de ignorar los "Note Off" que no se corresponden con el mensaje "Note On" inmediatamente anterior.
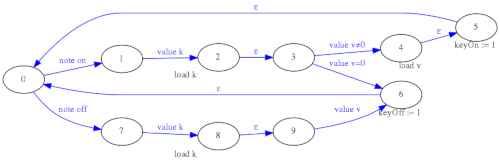
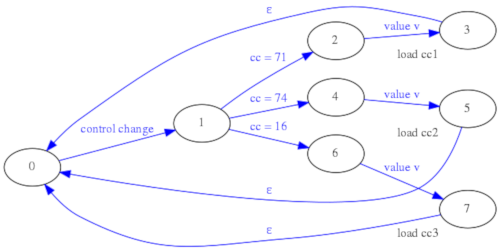
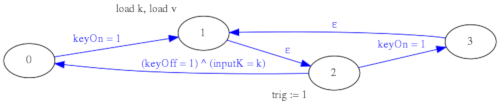
De esta forma, aunque aparentemente se ha complicado el diseño, se han separado los problemas y es más sencillo introducir modificaciones y depurar errores en las máquinas de estado. Cada una por separado es más sencilla y fácil de trazar que una hipotética máquina de estados única para todo.
Además de la mejora en el procesado de los mensajes "Note On" y "Note Off", este parser ya reconoce mensajes de tipo "Control Change", en concreto para tres valores prefijados de controlador: 71, 74 y 16, que se asignarán en el sintetizador a la frecuencia de corte del filtro, la resonancia del filtro y la ganancia de entrada del filtro.
Filtro paso bajo de segundo orden
Se ha optado por la implementación estándar de un filtro de estado variable (state variable filter). Se trata de un filtro de segundo orden (dos polos) que genera simultáneamente 3 salidas:
- paso bajo (con pendiente de filtrado de 12 dB/octava)
- paso alto (con pendiente de filtrado de 12 dB/octava)
- paso banda (con pendiente de filtrado de 6 dB/octava)
No son grandes pendientes de filtrado pero siempre se pueden mejorar poniendo varios filtros en cascada. La implementación que se ha utilizado es la descrita en el libro "Musical Applications of Microprocessors" de Hal Chamberlin (dicha implementación ya fue usada sobre un microcontrolador en este post). El filtro de estado variable viene determinado por el siguiente sistema de ecuaciones en diferencias finitas:
$$pasoAlto[n] = entrada - ({r \times pasoBanda[n-1]}) - pasoBajo[n]$$
$$pasoBanda[n] = ({f \times pasoAlto[n]}) + pasoBanda[n - 1]$$
$$pasoBajo[n] = ({f \times pasoBanda[n - 1]}) + pasoBajo[n - 1]$$
Siendo:
$$f = 2\sin\left({\pi F_c \over F_s}\right)$$
$$r = {1 \over Q}$$
Siendo $F_c$ la frecuencia de corte del filtro, $F_s$ la frecuencia de muestreo y $Q$ la Q del filtro (la resonancia).
Si se reordenan las ecuaciones en diferencias:
$$pasoBajo[n] = ({f \times pasoBanda[n - 1]}) + pasoBajo[n - 1]$$
$$pasoAlto[n] = entrada - ({r \times pasoBanda[n - 1]}) - pasoBajo[n]$$
$$pasoBanda[n] = ({f \times pasoAlto[n]}) + pasoBanda[n - 1]$$
Podemos olvidarnos de los índices:
pasoBajo += f * pasoBanda
pasoAlto = entrada - (r * pasoBanda) - pasoBajo
pasoBanda += f * pasoAlto
Como se puede apreciar es preciso mantener en memoria (registro) al menos las variables pasoBajo y pasoBanda entre que se procesa una muestra y la siguiente (se trata de un filtro digital de segundo orden).
Para implementar dicho filtro sobre FPGA lo que necesitaremos serán básicamente los siguientes elementos:
- Al menos tres registros en los que almacenaremos los valores "pasoBajo", "pasoBanda" y "pasoAlto" (aunque realmente podríamos no gastar un registro para "pasoAlto", lo vamos a incluir para poder disponer de esa salida en el módulo).
- Una unidad de suma con multiplicación: Un módulo combinacional que realiza la operación: A = (B * C) + D (en muchos casos D = A, por lo que se puede ver como A += B * C)
- Una máquina de estados para controlar qué operandos y operaciones se hacen en cada momento.
Con estos elemento y teniendo en cuenta las ecuaciones anteriores, podemos hacer una propuesta de secuenciación de operaciones como sigue:
1. LP := (cutoff * BP) + LP
2. HP := (0 * x ) + IN
3. HP := (-reso * BP) + HP
4. HP := (-1 * LP) + HP
5. BP := (cutoff * HP) + BP
Cada paso requiere un único ciclo de reloj por lo que bastará con implementar una máquina de estados que, por cada muestra que llegue, pase por los 5 estados de forma secuencial para que los registros LP, BP y HP (LowPass, BandPass y HighPass) tengan los valores de salida del filtro que necesitamos. Nótese que será preciso utilizar aritmética de punto fijo y en nuestro caso se ha optado por un formato Q16.16 (16 bits de parte entera y 16 bits de parte fraccionaria).
A continuación puede verse como quedaría la implementación del filtro en VHDL:
library ieee; use ieee.std_logic_1164.all; use ieee.numeric_std.all; entity StateVariableFilter is port ( Reset : in std_logic; Clk : in std_logic; EnableIn : in std_logic; SampleIn : in std_logic_vector(15 downto 0); CutOffIn : in std_logic_vector(31 downto 0); -- 0..1 fixed point Q16.16 ResonanceIn : in std_logic_vector(31 downto 0); -- 0..1 fixed point Q16.16 SampleOut : out std_logic_vector(15 downto 0); EnableOut : out std_logic ); end entity; architecture RTL of StateVariableFilter is signal LPDBus : std_logic_vector(31 downto 0); signal LPQBus : std_logic_vector(31 downto 0); signal HPDBus : std_logic_vector(31 downto 0); signal HPQBus : std_logic_vector(31 downto 0); signal BPDBus : std_logic_vector(31 downto 0); signal BPQBus : std_logic_vector(31 downto 0); signal MultOperandA : std_logic_vector(31 downto 0); signal MultOperandB : std_logic_vector(31 downto 0); signal MultResult64 : std_logic_vector(63 downto 0); signal MultResult : std_logic_vector(31 downto 0); signal AddOperandB : std_logic_vector(31 downto 0); signal AddResult : std_logic_vector(31 downto 0); signal NegResonance : std_logic_vector(31 downto 0); signal FSMDBus : std_logic_vector(2 downto 0); signal FSMQBus : std_logic_vector(2 downto 0); begin process (Clk) begin if (Clk'event and (Clk = '1')) then LPQBus <= LPDBus; end if; end process; process (Clk) begin if (Clk'event and (Clk = '1')) then HPQBus <= HPDBus; end if; end process; process (Clk) begin if (Clk'event and (Clk = '1')) then BPQBus <= BPDBus; end if; end process; process (Clk) begin if (Clk'event and (Clk = '1')) then FSMQBus <= FSMDBus; end if; end process; NegResonance <= std_logic_vector(to_signed(-to_integer(signed(ResonanceIn)), 32)); MultOperandA <= CutOffIn when ((FSMQBus = "001") or (FSMQBus = "101")) else NegResonance when (FSMQBus = "011") else std_logic_vector(to_signed(-65536, 32)) when (FSMQBus = "100") else -- -65536 es -1 en notación Q16.16 std_logic_vector(to_signed(0, 32)); MultOperandB <= LPQBus when (FSMQBus = "100") else BPQBus when ((FSMQBus = "001") or (FSMQBus = "011")) else HPQBus; AddOperandB <= LPQBus when (FSMQBus = "001") else BPQBus when (FSMQBus = "101") else HPQBus when ((FSMQBus = "011") or (FSMQBus = "100")) else std_logic_vector(to_signed(to_integer(signed(SampleIn)), 32)); --MultResult64 <= std_logic_vector(to_signed(to_integer(signed(MultOperandA)) * to_integer(signed(MultOperandB)), 64)); MultResult64 <= std_logic_vector(signed(MultOperandA) * signed(MultOperandB)); MultResult <= MultResult64(47 downto 16); --AddResult <= std_logic_vector(to_signed(to_integer(signed(MultResult)) + to_integer(signed(AddOperandB)), 32)); AddResult <= std_logic_vector(signed(MultResult) + signed(AddOperandB)); LPDBus <= std_logic_vector(to_signed(0, 32)) when (Reset = '1') else AddResult when (FSMQBus = "001") else LPQBus; HPDBus <= std_logic_vector(to_signed(0, 32)) when (Reset = '1') else AddResult when ((FSMQBus = "011") or (FSMQBus = "100") or (FSMQBus = "010")) else HPQBus; BPDBus <= std_logic_vector(to_signed(0, 32)) when (Reset = '1') else AddResult when (FSMQBus = "101") else BPQBus; -- fsm -- LP += cutoff * BP -- HP = in - (resonance * BP) - LP -- BP += cutoff * HP FSMDBus <= "000" when ((Reset = '1') or (FSMQBus = "110")) else -- MultOperandA MultOperandB AddOperandB "001" when ((FSMQBus = "000") and (EnableIn = '1')) else -- LP := cutoff * BP + LP "010" when (FSMQBus = "001") else -- HP := 0 * x + IN "011" when (FSMQBus = "010") else -- HP := -reso * BP + HP "100" when (FSMQBus = "011") else -- HP := -1 * LP + HP "101" when (FSMQBus = "100") else -- BP := cutoff * HP + BP "110" when (FSMQBus = "101") else "000"; EnableOut <= '1' when (FSMQBus = "110") else '0'; SampleOut <= std_logic_vector(to_signed(-32768, 16)) when (to_integer(signed(LPQBus)) < -32768) else std_logic_vector(to_signed(32767, 16)) when (to_integer(signed(LPQBus)) > 32767) else LPQBus(15 downto 0); end architecture;
La máquina de estados espera hasta que la entrada "EnableIn" se ponga a "1", dicho evento es la señal que indica al filtro que debe realizar una iteración (i.e. calcular la siguiente muestra a partir de la entrada "SampleIn").
Todo el código está disponible en la sección soft.
[ 1 comentario ] ( 2277 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 4575 )
( 3 / 4575 )Tradicionalmente, la síntesis y el procesado de sonido digital siempre se ha delegado a nivel hardware en el uso de DSPs. El uso de FPGAs para sustituir DSPs es una tendencia actual derivada del abaratamiento de las FPGAs y de la incursión de las mismas dentro del mundo de la electrónica amateur y DIY. Actualmente una FPGA media tiene suficiente potencia para llevar a cabo múltiples operaciones DSP a una velocidad incluso mayor. El problema con las FPGAs es la forma de programarlas, que requiere un pensamiento abstracto de tipo diferente al razonamiento algorítmico tradicional que se utiliza para programar CPUs y DSPs estándar. Este post se introducirá en el diseño y la implementación de un sintetizador monofónico muy simple sobre una FPGA.
La idea
La idea de esta primera versión es implementar un sintetizador monofónico con un único oscilador de diente de sierra, que sólo lea mensajes de tipo NoteOn y NoteOff y que reproduzca el sonido a través de un DAC I2S.
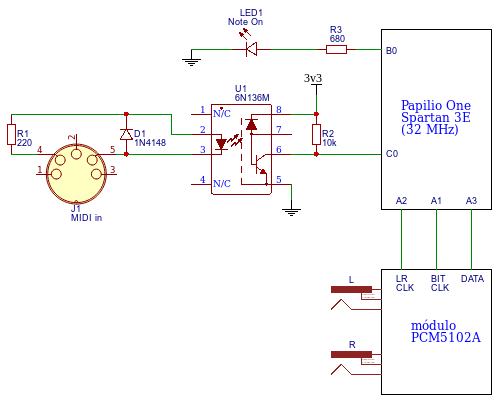
Como se puede apreciar se trata del típico circuito de entrada MIDI con optoacoplador más un PCM5102A como DAC I2S de alta calidad. Los mensajes MIDI de NoteOn se traducen en tonos que genera el oscilador.
El interfaz de salida I2S para el DAC externo
El protocolo I2S es un estándar definido para transportar sonido digital a muy cortas distancias (dentro de una misma placa, por ejemplo). Es estándar de facto en casi la totalidad de los conversores DAC y ADC de alta calidad del mercado de todos los fabricantes y se trata de un protocolo relativamente ligero y fácil de implementar.
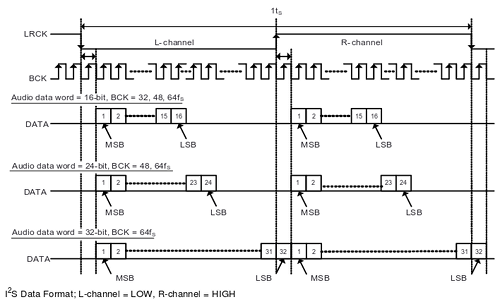
(imagen © Texas Instruments Incorporated, extraida con permiso de la hoja de datos del PCM5102A)
Existe una variante del I2S denominada "Left Justified" que simplifica el uso del reloj LR, evitando el desfase de un bit entre el envío de cada palabra para el canal izquierdo y el canal derecho:
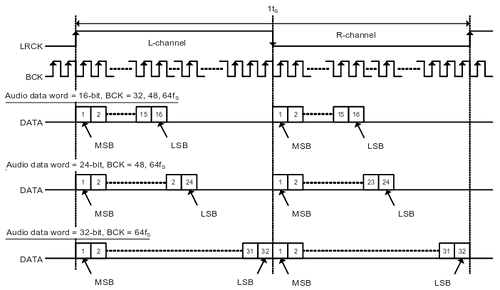
(imagen © Texas Instruments Incorporated, extraida con permiso de la hoja de datos del PCM5102A)
Y que es la variante I2S que se ha usado en este proyecto ya que es más fácil de implementar que el estándar original y actualmente todos los DACs del mercado la soportan. A continuación puede verse lo que sería el diagrama de bloques de la interfaz I2S-LJ dentro de la FPGA:
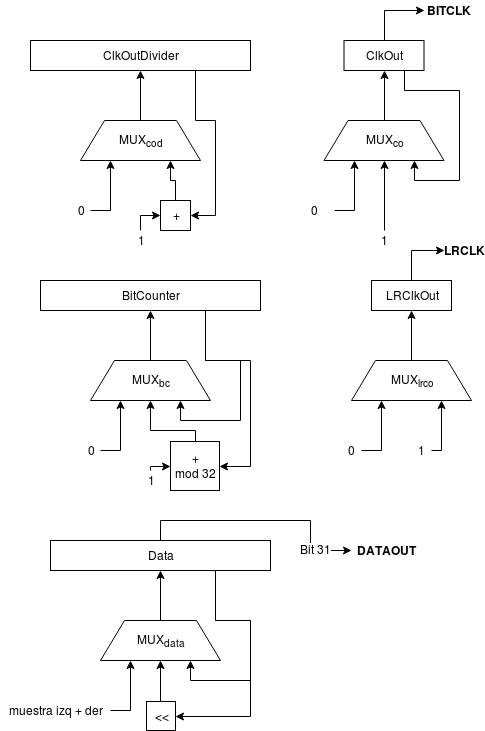
Las diferentes tablas de verdad de cada uno de los bloques combinacionales serían las siguientes:
| Entradas | Salidas | |
|---|---|---|
| ClkOutDivider == 22 | Reset | MUXcod |
| 0 | 0 | + |
| 0 | 1 | 0 |
| 1 | X | 0 |
| Entradas | Salidas | ||
|---|---|---|---|
| ClkOutDivider == 22 | ClkOutDivider == 10 | Reset | MUXco |
| 1 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| en otro caso | ClkOut | ||
| Entradas | Salidas | |
|---|---|---|
| ClkOutDivider == 22 | Reset | MUXbc |
| X | 1 | 0 |
| 1 | 0 | + mod 32 |
| en otro caso | BitCounter | |
| Entradas | Salidas | |
|---|---|---|
| BitCounter < 16 | Reset | MUXlrco |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | X | 1 |
| Entradas | Salidas | |
|---|---|---|
| ClkOutDivider == 22 | BitCounter == 31 | MUXdata |
| 0 | X | data |
| 1 | 0 | << |
| 1 | 1 | muestra izq + der |
Como se puede apreciar el mecanismo se basa en meter en un registro de desplazamiento de 32 bits las dos palabras de 16 bits de cada canal (izquierdo + derecho) e ir emitiendo bit a bit ese registro cambiando la polaridad de la señal LRCLK cada 16 bits para indicar canal izquierdo o canal derecho.
El oscilador
El oscilador se ha implementado como un sencillo acumulador de fase.
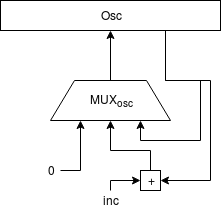
Como lo que se busca es un oscilador de diente de sierra, lo más sencillo es aprovechar el comportamiento natural de cualquier acumulador que, cuando se desborda "da la vuelta". Esto simplifica enormemente todo el diseño ya que, de forma natural, la señal resultante tiene forma de diente de sierra.
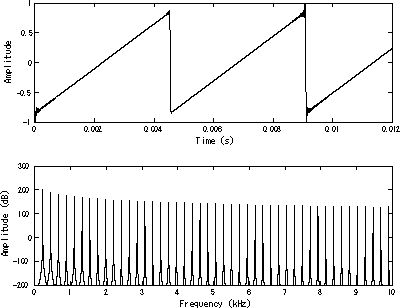
(imagen de dominio público extraida de Wikipedia)
Por cada nueva muestra que debe ser calculada, el acumulador es incrementado en una cantidad determinada, lo que provoca que su valor crezca de forma lineal (la rampa del diente de sierra). Al cabo de una cantidad suficiente de muestras, el acumulador se desbordará y "dará la vuelta" empezando de nuevo desde abajo (el "pico" del diente de sierra).
La cantidad que se use para ir incrementando el acumulador de fase determinará la frecuencia de la señal del oscilador:
$$DivisorFrecuenciaRelojI2S = {{32000000 Hz \over 44100 Hz} \over 32 bits}$$
$$inc = {{f \times 65536} \over {{32000000Hz \over DivisorFrecuenciaRelojI2S} \over 32 bits}} \times 65536$$
El incremento (inc) debe estar en formato Q16.16 (punto fijo de 16 bits de parte entera y 16 bits de parte fraccionaria), que es el formato usado por el acumulador de fase del oscilador.
Nótese que el oscilador no se incrementa en cada ciclo de reloj de la FPGA, sino cada vez que se requiere una nueva muestra por parte de la interfaz I2S-LJ para emitirla al DAC.
El parser MIDI
El módulo de procesamiento MIDI se encarga de implementar un receptor UART sencillo a 31250 baudios y una máquina de estados que vaya leyendos los datos MIDI de entrada y determinando en cada momento si hay que reproducir una nota en el oscilador (y con qué frecuencia) o no.
La UART se implementa de forma muy sencilla usando un registro de desplazamiento y un contador para medir el tiempo equivalente a 1.5 bits y a 1 bit.
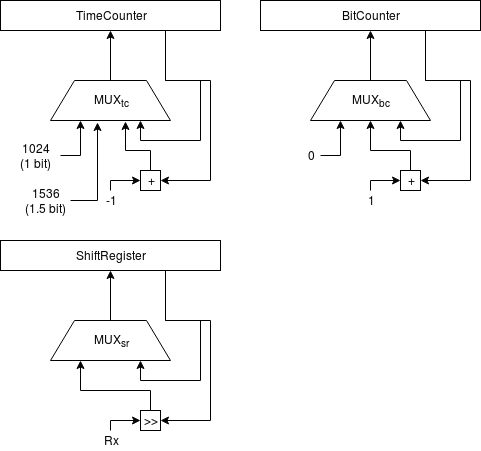
Y usando la siguiente máquina de estados:
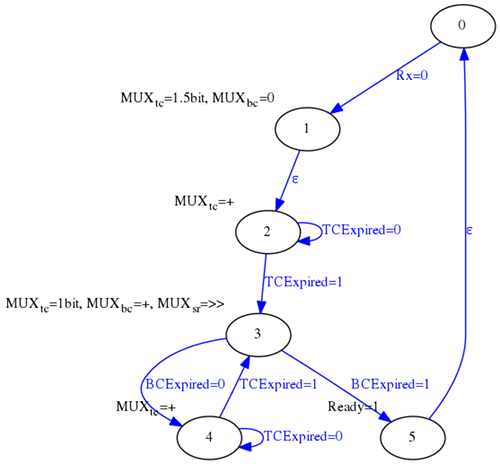
En una entrada anterior de este blog se abordó este proyecto de forma separada. Lo que se ha hecho en este caso ha sido simplificar aquel esquema para que cupiese todo dentro de un único fichero VHDL.
Una vez implementado el receptor UART, el parser MIDI se puede implementar mediante una sencilla máquina de estados que sólo detecte eventos NoteOn y NoteOff.
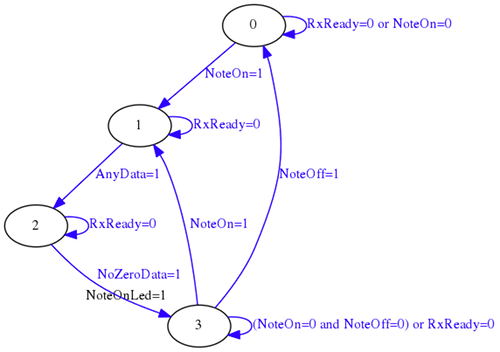
El parser MIDI en este caso no sólo determina qué nota debe ser reproducida, sino que usando una ROM interna, determina el valor de incremento que debe ser usado por el módulo oscilador para generar el tono correspondiente.
library ieee; use ieee.std_logic_1164.all; use ieee.numeric_std.all; entity NotesRom is port ( AddressIn : in std_logic_vector(6 downto 0); DataOut : out std_logic_vector(31 downto 0) ); end entity; architecture RTL of NotesRom is type RomType is array (0 to 127) of std_logic_vector(31 downto 0); constant Data : RomType := ( x"00000000", -- note 0 x"000cdf51", -- note 1 x"000da345", -- note 2 x"000e72df", -- note 3 x"000f4ed1", -- note 4 x"001037d7", -- note 5 x"00112eb9", -- note 6 x"00123449", -- note 7 x"00134966", -- note 8 x"00146efe", -- note 9 x"0015a60b", -- note 10 x"0016ef97", -- note 11 . . . . . . . . . x"368d1251", -- note 122 x"39cb7a59", -- note 123 x"3d3b4348", -- note 124 x"40df5cc9", -- note 125 x"44bae33a", -- note 126 x"48d12253" -- note 127 ); begin DataOut <= Data(to_integer(unsigned(AddressIn))); end architecture;
Para generar este conjunto de valores se hizo un pequeño programa en C++ que convirtió el valor de cada nota MIDI en el valor de incremento correspondiente para que el oscilador emita a esa frecuencia:
#include <iostream> #include <iomanip> #include <stdint.h> #include <math.h> using namespace std; double getFreq(uint8_t midiNote) { const double A4_FREQ = 440; const int32_t A4_MIDI_NOTE = 69; return A4_FREQ * pow(2.0, ((double) (((int32_t) midiNote) - A4_MIDI_NOTE)) / 12.0); } uint32_t getInc(uint8_t midiNote) { const uint32_t CLK_FREQ = 32000000; const uint32_t SAMPLE_RATE = 44100; double freq = getFreq(midiNote); double div = (((double) CLK_FREQ) / SAMPLE_RATE) / 32; double inc = (freq * 65536) / ((CLK_FREQ / div) / 32); uint32_t ret = round(inc * 65536); return ret; } int main() { for (uint8_t n = 0; n < 128; n++) cout << "\t\tx\"" << hex << setw(8) << setfill('0') << getInc(n) << "\", -- note " << dec << setw(0) << setfill(' ') << ((int) n) << endl; return 0; }
Compilando este programa y ejecutándolo, genera en la salida estándar los valores de incremento de todas las 127 notas MIDI posibles:
g++ -c -o notes_rom_generator.o notes_rom_generator.cc
g++ -o notes_rom_generator notes_rom_generator.o
./notes_rom_generator
Todo junto
A la hora de ponerlo todo junto, basta con interconectar los tres bloques:
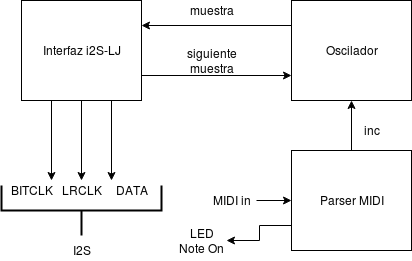
Implementación sobre cualquier FPGA
La implementación se ha desarrollado sobre una Spartan3E de Xilinx a 32 MHz pero el proyecto se puede meter en cualquier FPGA siempre y cuando se ajusten las ecuaciones y las constantes para tener en cuenta las diferentes frecuencias de reloj. En caso de que queramos meter el sintetizador en una FPGA que vaya a otra frecuencia de reloj habría que realizar los siguientes cambios:
1. Las constantes CLK_OUT_DIV y CLK_OUT_DIV_BITS de LJI2SOutput.vhd deben se recalculadas.
2. Las constantes TIME_COUNTER_BITS, TIME_COUNTER_1BIT y TIME_COUNTER_1_5BIT de UartRx.vhd deben ser recalculadas.
3. La constante CLK_FREQ dentro de notes_rom_generator.cc debe ser cambiada, hay que recompilar el programa y colocar la salida generada como los nuevos valores de NotesRom.vhd.
Todo el código fuente puede descargarse de la sección soft.
[ añadir comentario ] ( 3511 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 4717 )
( 3 / 4717 )
 Calendario
Calendario




