Un vúmetro no es más que un medidor gráfico de intensidad de señal de audio. En este caso vamos a abordar una implementación muy sencilla y lineal (no logarítmica).

Entrada analógica
La entrada analógica del microcontrolador AVR en el Arduino permite medir entre 0 y 5 voltios con una precisión de 10 bits, de 0 a 1023. 0 se corresponde con 0 voltios y 1023 se corresponde con 5 voltios. Para obtener la intensidad de señal en una de las entradas analógicas, realizamos los siguientes pasos:
1. Amplificación
2. Detección de envolvente
La amplificación se ha implementado construyendo una sencilla etapa estándar de amplificación basada en un transistor NPN con configuración de emisor común:
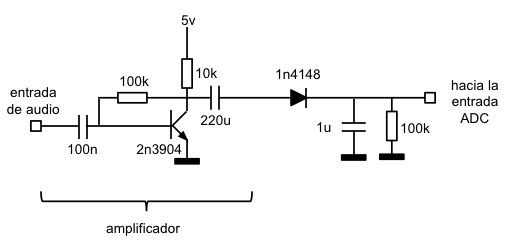
La señal de entrada es una señal de audio en alterna (en este caso la he conectado a la salida de auriculares de mi móvil). Dicha señal, al pasar por el circuito de amplificación se invierte en fase (no nos importa) y, lo más importante, se amplifica. La señal de salida es también en alterna (el condensador de salida elimina la componente de continua) y pasa la siguiente parte del circuito: el detector de envolvente.
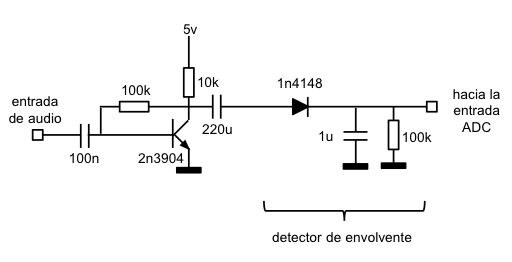
Un detector de envolvente es un circuito que, a partir de una señal de entrada, determina su envolvente:
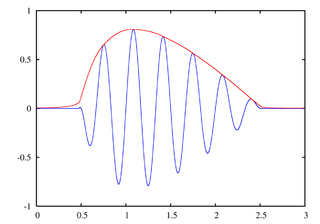
(imagen extraida de Wikimedia Commons)
El circuito detector de envolvente es muy sencillo: La señal alterna, al hacerla pasar por un diodo, se rectifica y sólo deja pasar los semiciclos positivos. En cada uno de los semiciclos positivos de la señal se carga el condensador y, durante las pausas entre semiciclos, en ausencia de corriente que pase por el diodo, el condensador se descarga lentamente a través de la resistencia, así hasta el siguiente ciclo, que se repite el proceso. El resultado en la salida es una señal que “sigue” de forma aproximada a los picos de la señal de audio que hay en la entrada.
Hay que elegir correctamente los valores del condensador y la resistencia: Un valor de condensador muy bajo hará que se descargue rápidamente mientras que un valor de condensador muy alto hará que tarde excesivamente en cargarse. En el caso de la resistencia de descarga del condensador un valor muy alto hará que el condensador apenas se descargue en las pausas entre ciclos (lo que puede provocar que los ciclos se “sumen” a medida que llegan) y un valor muy bajo hará que el condensador se descargue muy rápido, perdiendo el efecto de seguimiento de envolvente.
Display LCD
En post anteriores de este blog publiqué varias clases C++ para la gestión de displays LCD. En este caso he reutilizado la clase “Lcd20x4” de proyectos anteriores, redefiniendo de forma estática 5 de los caracteres definibles por el usuario.
Para implementar una barra horizontal hay que tener en cuenta que tenemos 20 columnas y que cada carácter tiene 5 columnas de puntos: En total tenemos 100 pixels en horizontal para un display LCD de 20x4. Si definimos los caracteres de la siguiente forma:
* . . . .
* . . . .
* . . . .
* . . . . --> 1
* . . . .
* . . . .
* . . . .
* * . . .
* * . . .
* * . . .
* * . . . --> 2
* * . . .
* * . . .
* * . . .
...
* * * * *
* * * * *
* * * * *
* * * * * --> 5
* * * * *
* * * * *
* * * * *
Utilizando este método de visualización, la barra LCD podrá adoptar valores entre 0 y 100. El pseudocódigo para visualizar un valor “v” será:
procedimiento mostrar_valor(v) // 0 <= v <= 100
numCaracteresTotalmenteLlenos := parte entera de (v / 5)
valorCaracterParcial := (v mod 5)
ir_coordenada(0, 0)
para x := 1 hasta numCaracteresTotalmenteLlenos hacer
escribir_carácter(5)
fin para
escribir_carácter(valorCaracterParcial)
para x := (numCaracteresTotalmenteLlenos + 2) hasta 20 hacer
escribir_carácter(0)
fin para
fin procedimiento
Como se puede ver, para cada valor “v” que se quiera visualizar en la barra, se escribe toda una fila horizontal del display LCD. La visualización puede optimizarse si partimos de la base de que la diferencia entre un valor “v” enviado en un instante “t” y el valor “v” enviado al display en un instante “t + d” no va a variar mucho si “d” es lo suficientemente pequeño. En nuestro caso vamos a hacer un muestreo de la entrada analógica cada 50ms por lo que la “v” no va a variar excesivamente entre un instante de muestreo y el siguiente.
Si asumimos que la “v” no va a variar mucho podemos enviar al LCD sólo los cambios:
barraLogica[20]
barraFisica[20]
procedimiento mostrar_valor(v)
numCaracteresTotalmenteLlenos := parte entera de (v / 5)
valorCaracterParcial := (v mod 5)
j := 0
para x := 1 hasta numCaracteresTotalmenteLlenos hacer
barraLogica[j] := 5
j := j + 1
fin para
barraLogica[j] := valorCaracterParcial
j := j + 1
para x := (numCaracteresTotalmenteLlenos + 2) hasta 20 hacer
barraLogica[j] := 0
j := j + 1
fin para
fin procedimiento
procedimiento actualiza
dentroCambio := NO
inicioCambio := -1
para j := 0 hasta 19 hacer
si (dentroCambio) entonces
si (barraFisica[j] = barraLogica[j]) entonces
escribir_barra_fisica(inicioCambio, j)
dentroCambio := NO
fin si
en otro caso
si (barraFisica[j] <> barraLogica[j]) entonces
inicioCambio := j
dentroCambio := SI
fin si
fin si
barraFisica[j] := barraLogica[j]
fin para
si (dentroCambio) entonces
escribir_barra_fisica(inicioCambio, 19)
fin si
fin procedimiento
El procedimiento “actualiza” se ejecutará de forma periódica y, como se puede ver, sólo envía al display LCD los caracteres que cambien. Esta forma de refresco del display LCD es más eficiente y nos permite tasas de muestreo mayores.
En el siguiente vídeo puede verse el circuito en acción:
El código en C++ puede descargarse de la sección soft.
[ añadir comentario ] ( 2976 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 17140 )
( 3 / 17140 )El control de displays LCD alfanuméricos desde microcontroladores es un tópico ampliamente abordado en muchas webs y tutoriales. El juego de caracteres utilizado por este tipo de displays es de tipo ASCII con algunos símbolos adicionales, sobre todo asiáticos, y se echan en falta varios de los símbolos propios del español (tildes, diéresis, etc.). A lo largo de este post se plantea un sencillo algoritmo de gestión del display LCD que permite la utilización de texto en español de forma transparente al usuario.
Características del display
Los displays LCD alfanuméricos estándar almacenan los mapas de bits (los dibujos) de su juego de caracteres en una ROM interna, con la excepción de los 8 primeros caracteres (del 0 al 7). Los mapas de bits de estos 8 primeros caracteres se almacenan en una parte de la RAM del LCD denominada CGRAM (Character Generator RAM). Es esta parte de la RAM la que hay que utilizar para representar los caracteres extendidos no ASCII del español en nuestro display.
El mapa de bits de cada carácter está formado por una matriz de 5x7 puntos que se almacena en la CGRAM como 8 bytes consecutivos: 1 byte por cada línea horizontal (de la cual sólo son significativos los 5 bits más bajos) y un 1 byte adicional para la línea de cursor que siempre se pone a 0 para displays de 5x7. Como son configurables sólo los 8 primeros caracteres del juego de caracteres, esto nos da 8 * 8 = 64 bytes para la CGRAM.
. . . x . 0 0 0 1 0
. . x . . 0 0 1 0 0
. x x x . 0 1 1 1 0
á --> . . . . x --> 0 0 0 0 1
. x x x x 0 1 1 1 1
x . . . x 1 0 0 0 1
. x x x x 0 1 1 1 1
. . . . . 0 0 0 0 0
Gestión de los caracteres
En español tenemos 16 caracteres que se salen de la simbología ASCII:
á é í ó ú ü ñ Á É Í Ó Ú Ü Ñ ¿ ¡
Como no es posible cargar en la CGRAM los mapas de bits de estos 16 caracteres de forma simultánea, es necesario implementar algún tipo de gestión a nivel software que cargue en CGRAM sólo los caracteres que necesitamos en cada momento.
Para la gestión de los caracteres se han utilizado las siguientes estructuras de datos (en pseudocódigo):
EntradaTabla {
caracterLatin1
mapaDeBits
caracterLcd
caracterLcdDefecto
vecesUsado
marcaCarga
}
EntradaTabla tabla[16]
Cola caracteresLcdDisponiblesCada entrada de la tabla de caracteres especiales incluye el carácter “ISO-8859-1” o “latin1” correspondiente y el mapa de bits que lo dibuja en el display. caracterLcd es el carácter del LCD (1 al 7, no vamos a usar la entrada 0 por si acaso) que está mapeando a este carácter especial. caracterLcdDefecto es el carácter de la ROM que mapeará a este carácter latin1 en caso de que no esté disponible ningún hueco en la CGRAM (por ejemplo ‘á’ tiene como carácter por defecto ‘a’).
vecesUsado indica cuántas veces está siendo usado esa entrada de la tabla de caracteres extendidos: cada vez que se utiliza un carácter especial, se incrementa este contador de la entrada correspondiente y cada vez que se deja de utilizar en alguna parte de la pantalla (se borra o se sustituye por otro), se decrementa este contador de la entrada correspondiente. Cuando un contador llega a 0, el hueco que ocupaba esa entrada en la CGRAM es marcado como vacío (metido en la cola de caracteres LCD disponibles.
marcaCarga indica cuando una entrada de la tabla debe ser cargada en la CGRAM. La carga de los bitmaps de las entradas marcadas se realiza a posteiori para no influir en la escritura de los caracteres. Primero se escribe en la DDRAM (la memoria de pantalla) y al final, si es necesario enviar bitmaps de caracteres no ASCII, se escribe en la CGRAM.
inicializar(EntradaTabla e)
e.caracterLcd = 0
e.vecesUsado = 0
e.marcaCarga = NO
fin
inicializarCola
meter(caracteresLcdDisponibles, 1)
meter(caracteresLcdDisponibles, 2)
meter(caracteresLcdDisponibles, 3)
meter(caracteresLcdDisponibles, 4)
meter(caracteresLcdDisponibles, 5)
meter(caracteresLcdDisponibles, 6)
meter(caracteresLcdDisponibles, 7)
fin
buscarEntrada(c) {
Devuelve la entrada en “tabla” que cumpla “caracterLatin1 == c”, o NULL en caso de no haber ninguna entrada.
fin
reemplazarCaracter(nuevo, viejo)
EntradaTabla e = buscarEntrada(viejo)
si (e != NULL) {
e.vecesUsado = e.vecesUsado - 1
si (e.vecesUsado == 0) {
meter(caracteresLcdDisponibles, e.caracterLcd)
e.caracterLcd = 0
fin si
fin si
e = buscarEntrada(nuevo);
si (e == NULL)
devolver nuevo
en otro caso
si (e.caracterLcd > 0)
e.vecesUsado = e.vecesUsado + 1
en otro caso
si (caracteresLcdDisponibles está vacía)
devolver e.caracterLcdDefecto
e.caracterLcd = sacar(caracteresLcdDisponibles)
e.vecesUsado = 1
e.marcaCarga = SI
fin si
devolver e.caracterLcd
fin si
fin
procesar
para todos los segmentos de texto que haya que cambiar en el display
para todos los caracteres del segmento de texto
nuevo = nuevo carácter
viejo = actual carácter
v = reemplazarCaracter(nuevo, viejo)
emitir(v)
fin para
fin para
para todas las entradas e de la tabla con marcaCarga = SI hacer
cargar e.mapaDeBits en la CGRAM correspondiente al carácter e.caracterLcd
e.marcaCarga = NO
fin para
fin
Ejemplo de traza
Imaginemos que tenemos la pantalla en blanco (recién inicializada): Todas las entradas de la tabla las tenemos inicializadas (caracterLcd=0, vecesUsado=0, marcaCarga=NO) y la cola “caracteresLcdDisponibles” inicializada con los 7 huecos.
Para escribir la palabra “Máquina”, el proceso irá llamando a “reemplazarCaracter” por cada nueva letra:
reemplazarCaracter(‘M’, ‘’)
No hay entrada en la tabla para el carácter ‘’
No hay entrada en la tabla para el carácter ‘M’
devuelve ‘M’
reemplazarCaracter(‘á’, ‘’)
No hay entrada en la tabla para el carácter ‘’
Hay una entrada e para el carácter ‘á’
como e.caracterLcd = 0, entonces
la cola de caracteres disponibles no está vacía
e.caracterLcd = 1
e.vecesUsado = 1
e.marcarCarga = SI
devuelve e.caracterLcd (1)
reemplazarCaracter(‘q’, ‘’)
No hay entrada en la tabla para el carácter ‘’
No hay entrada en la tabla para el carácter ‘q’
devuelve ‘q’
reemplazarCaracter(‘u’, ‘’)
No hay entrada en la tabla para el carácter ‘’
No hay entrada en la tabla para el carácter ‘u’
devuelve ‘u’
...
Al final del proceso de escritura de la cadena ‘Máquina’ tenemos que la cola de caracteres disponibles está así: [2, 3, 4, 5, 6, 7] y que la entrada de la tabla de caracteres correspondiente a la letra ‘á’ tiene caracterLcd=1, vecesUsado=1, el resto de entradas siguen como al principio.

De esta forma se va alojando espacio en la CGRAM del display LCD en función de los caracteres especiales que necesitamos en todo momento. Nótese que, en caso de que ya no nos queden huecos libres (la cola de huecos esté vacía), devolvemos el carácter por defecto.
Políticas alternativas de sustitución de caracteres
Una política alternativa podría ser establecer una prioridad por cada carácter de la tabla: en caso de vaciado de la cola de huecos, se sacrifica el carácter con menor prioridad de los que estén siendo usados en ese momento. Un criterio de prioridad podría ser en función del valor de “vecesUsado”. De esta forma se sacrificarían los caracteres menos usados.
Nótese que esta política de “sacrificado” de caracteres menos prioritarios obligaría a refrescar los caracteres a sacrificar y cambiarlos por los caracteres por defecto correspondientes. En todas las posiciones donde se encuentren.
En esta implementación no se lleva a cabo ninguna política de sacrificado de caracteres. Cuando la cola de caracteres disponibles se acaba, se imprime el carácter por defecto.
Implementación
Este algoritmo de gestión de caracteres extendidos para displays LCD se ha implementado sobre un Arduino Leonardo en C++.
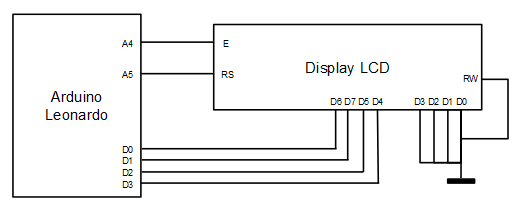
Se ha optado por una anchura de bus de 4 bits para minimizar el número de cables. El código fuente puede descargarse de la sección soft.
[ añadir comentario ] ( 2975 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 3992 )
( 3 / 3992 )Ampliando un post anterior en el que desarrollé un juego de tres en raya con el Arduino, he desarrollado una implementación “inteligente” del mismo. En la anterior versión, si bien el jugador jugaba contra la máquina, las posiciones que jugaba la máquina eran totalmente aleatorias y no seguían ningún criterio. En este caso la máquina utiliza un algoritmo de decisión (el minimax) para calcular el siguiente movimiento y así intentar ganar a su oponente humano.
Antecedentes
En la implementación anterior del tres en raya teníamos una clase abstracta denominada TTTGamePlayer de la cual heredaban las clases TTTHumanGamePlayer y TTTRandomGamePlayer. TTTHumanGamePlayer además de heredar de TTTGamePlayer, también heredaba de KeyMatrixListener, de esta forma los eventos de los pulsadores se transforman en movimientos del jugador humano.
La clase TTTRandomGamePlayer era una clase que inicializaba una semilla aleatoria. Dentro de esta clase el método getSpot(), que es el método virtual puro de TTTGamePlayer que debe devolver el movimiento que desea realizar el jugador, devolvía en este caso una posición aleatoria de entre todas las posiciones libres que quedaban en el tablero.
Algoritmo Minimax
El algoritmo minimax es un algoritmo de decisión muy simple desarrollado a partir del Teorema Minimax de John von Neumann en 1926 (para juegos de suma cero e información perfecta). El algoritmo es muy sencillo:
- Cuando nos toque mover a nosotros, calculamos el árbol de decisión del juego.
- Los nodos hoja del árbol representarán todas las posibles formas de terminar el juego. Asignamos a cada uno de los nodos hoja del árbol un valor numérico directamente proporcional a nuestro beneficio (o inversamente proporcional al beneficio de nuestro oponente).
- Vamos ascendiendo en el árbol escogiendo, alternativamente, el mínimo o el máximo de los hijos (minimax) en función de si cada decisión debe ser tomada por mí o por mi oponente (yo busco maximizar mi beneficio y mi oponente busca minimizarlo o, lo que es lo mismo, maximizar el suyo propio), así hasta la raíz. De esta forma podemos elegir el movimiento que minimize nuestra pérdida esperada.
Con un ejemplo del 3 en raya se ve mejor. Imaginemos que somos X y que nos toca mover a nosotros:
o x x
x . . sig. mov. = x, beneficio = max(-1, -1, 0) = 0
o o .
o x x
x x . sig. mov. = o, beneficio = min(0, -1) = -1
o o .
o x x
x x o sig. mov. = x, beneficio = max(0) = 0
o o .
o x x
x x o tablas, beneficio = 0
o o x
o x x
x x . gana o, beneficio = -1
o o o
o x x
x . x sig. mov. = o, beneficio = min(1, -1) = -1
o o .
o x x
x o x sig. mov. = x, beneficio = max(1) = 1
o o .
o x x
x o x gana x, beneficio = 1
o o x
o x x
x . x gana o, beneficio = -1
o o o
o x x
x . . sig. mov = o, beneficio = min(1, 0) = 0
o o x
o x x
x o . sig. mov. = x, beneficio = max(1) = 1
o o x
o x x
x o x gana x, beneficio = 1
o o x
o x x
x . o sig. mov. = x, beneficio = max(0) = 0
o o x
o x x
x x o tablas, beneficio = 0
o o x
A partir del nodo raíz, el beneficio máximo se corresponde con el movimiento:
o x x o x x
x . . ---> x . .
o o . o o x
En este caso “beneficio” se refiere a “beneficio para X”. Como se puede ver, partiendo del estado del tablero indicado por la raíz del árbol, el mejor movimiento será el de marcar la fila 3 y la columna 3.
Hardware
El montaje lo he realizado utilizando un Arduino Leonardo, conectando la matriz de pulsadores a los puertos A0, A1, A2, D11, D12 y D13
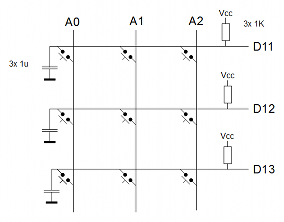
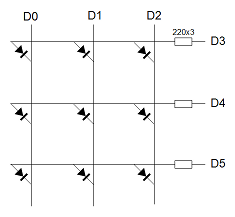
Y la matriz de leds a los puertos D0, D1, D2, D3, D4 y D5
Si vamos a realizar el montaje para otro modelo de Arduino hay que comprobar el mapeo de los puertos en el microcontrolador y modificar la implementación de las clases MyLedMatrixManager y MyKeyMatrixManager (como se trata de una implementación en C++, no tenemos a nuestra disposición la abstracción de puertos que nos proporciona el lenguaje Arduino).
Implementación
La clase TTTMinimaxGamePlayer es la que implementa el algoritmo minimax: Al igual que las clases TTTRandomGamePlayer y TTTHumanGamePlayer, hereda de TTTGamePlayer con la diferencia de que en su método getSpot() calcula el siguiente movimiento a realizar utilizando el algoritmo de decisión minimax.
uint8_t TTTMinimaxGamePlayer::getSpot() { uint8_t ret = 0; this->minimax(*this->board, true, ret); return ret; } int8_t TTTMinimaxGamePlayer::minimax(TTTGameBoard &board, bool me, uint8_t &bestMovement) { uint8_t winner = board.getWinner(); if (board.isFinished() || (winner != 0)) { int8_t ret = 0; if (winner == this->number) ret = 1; else if (winner == this->opponentNumber) ret = -1; return ret; } else { int8_t limit = 0; if (me) limit = -10; else limit = 10; TTTGameBoard auxBoard; uint8_t numMovements = 0; for (uint8_t m = board.getFirstAvailableMovement(); m != 0; m = board.getNextAvailableMovement(), numMovements++) { auxBoard.copyFrom(board); if (me) auxBoard.set(m, this->number); else auxBoard.set(m, this->opponentNumber); uint8_t childBestMovement; int8_t v = minimax(auxBoard, !me, childBestMovement); if (me) { if (v > limit) { limit = v; bestMovement = m; } } else { if (v < limit) { limit = v; bestMovement = m; } } } return limit; } }
Se trata de una implementación recursiva y el parametro “me” indica cuando se está simulando un movimiento propio (true) o un movimiento del oponente (false). A pesar de usarse una implementación recursiva, nótese que no se realizarán más de 8 llamadas recursivas: Cada nivel es un movimiento adicional y un tablero de 3 en raya sólo tiene 9 posiciones.
A modo de visión global, el diagrama de clases queda ahora así:
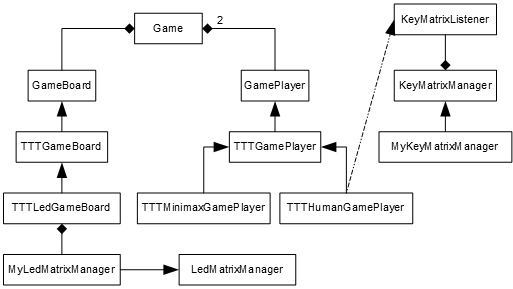
En la sección soft puede descargarse el código fuente del proyecto en C++. Aquí una pequeña guía sobre cómo desarrollar en C++ para el Arduino.
[ añadir comentario ] ( 3689 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 3958 )
( 3 / 3958 )El algoritmo de Ramer-Douglas-Peucker, a veces también denominado algoritmo de Douglas-Peucker a secas, es un algoritmo que fue desarrollado en los años 70 por Urs Ramer, David Douglas y Thomas Peucker. Dicho algoritmo permite reducir la cantidad de puntos en una ruta de segmentos rectilíneos utilizando un criterio de distancias. Es muy útil para la simplificación de rutas sobre mapas o para la optimización en el renderizado de imágenes vectoriales.
El algoritmo se basa en la técnica de divide y vencerás. Partiendo de una ruta inicial formada por un conjunto de N puntos, $p_0$ a $p_{n - 1}$ buscamos, de entre los puntos intermedios, el que esté más alejado de la recta que une $p_0$ y $p_{n - 1}$. Sea este punto $p_i$ y $d(i, 0, n - 1)$ la distancia entre $p_i$ y la recta que une $p_0$ con $p_{n - 1}$.
Si $d(i, 0, n - 1)$ supera un valor umbral que llamaremos $\varepsilon$, realizamos dos llamadas recursivas, una que ejecuta el algoritmo entre los puntos $p_0$ y $p_i$ y otra que ejecuta el algoritmo entre los puntos $p_i$ y $p_{n - 1}$.
Si $d(i, 0, n - 1)$ no supera el valor umbral de $\varepsilon$, descartamos de la ruta final todos los puntos intermedios entre $p_0$ y $p_{n - 1}$, esto es, descartamos todos los puntos $p_j$ tales que $i < j < n - 1$.
Con un ejemplo se ve mejor. Consideremos la siguiente ruta formada por 5 puntos, de $p_0$ a $p_4$ y consideremos un valor de $\varepsilon = 1.3$.
|
| 3
| 1 2
|
| 0
| 4
+-+-+-+-+-+-+-+-+-+
| 3
| 1 2
|
| 0
| 4
+-+-+-+-+-+-+-+-+-+
Inicialmente consideramos la recta que une $p_0$ con $p_4$ (el primero con el último) y buscamos el punto más alejado de ella. En nuestro caso es $p_3$ (lo he subrayado) y la distancia de la recta $\overline{p_0p_4}$ a $p_3$ es de 3.82 aproximadamente, dicho valor es superior a nuestro $\varepsilon$ (1.3) y, por tanto dividimos el problema en dos subproblemas de forma recursiva.
Invocamos, por un lado el algoritmo considerando la ruta formada por los puntos $p_0$ a $p_3$ y, por otro lado el mismo algoritmo considerando la ruta formada por los puntos $p_3$ a $p_4$. Este último caso es trivial ya que no hay puntos intermedios y, obviamente, no se puede descartar ningún punto entre $p_3$ y $p_4$.
Si consideramos ahora la ruta formada por los puntos $p_0$ a $p_3$.
|
| 3
| 1 2
|
| 0
| 4
+-+-+-+-+-+-+-+-+-+
| 3
| 1 2
|
| 0
| 4
+-+-+-+-+-+-+-+-+-+
Hacemos el mismo razonamiento: consideramos la recta que une el primer punto con el último ($p_0$ con $p_3$) y buscamos el punto intermedio más alejado de dicha recta. En este caso el punto más alejado de la recta que une $p_0$ con $p_3$ es $p_1$ (de nuevo subrayado) con una distancia aproximada de 1.34.
Como 1.34 es mayor que nuestro $\varepsilon$, volvemos a subdividir el problema en dos nuevos problemas más pequeños. Por un lado llamamos al algoritmo con la ruta formada por los puntos $p_0$ y $p_1$ y por otro lado llamamos al algoritmo con la ruta formada por los puntos $p_1$ a $p_3$. El cálculo del algoritmo para dos puntos, al igual que pasó anteriormente con $p_3$ y $p_4$ es trivial ya que, al no haber puntos intermedios, no es posible descartar ningún punto. Por tanto nos centraremos en el caso de la ruta entre $p_1$ y $p_3$.
|
| 3
| 1 2
|
| 0
| 4
+-+-+-+-+-+-+-+-+-+
| 3
| 1 2
|
| 0
| 4
+-+-+-+-+-+-+-+-+-+
Recordemos que, hasta ahora, no se ha descartado ningún punto para la ruta final. Para la ruta formada por los puntos $p_1$ a $p_3$, el punto más alejado de la recta entre $p_1$ y $p_3$ es $p_2$ con una distancia de aproximadamente 0.39. Dicha distancia sí que es menor que nuestro umbral $\varepsilon$, por tanto descartamos todos los puntos intermedios entre $p_1$ y $p_3$.
|
| 3
| 1
|
| 0
| 4
+-+-+-+-+-+-+-+-+-+
| 3
| 1
|
| 0
| 4
+-+-+-+-+-+-+-+-+-+
Como se puede ver, el algoritmo finalmente ha descartado el punto $p_2$ de la ruta.
A continuación se puede ver cómo sería el pseudocódigo:
ramer_douglas_peucker(vector, epsilon, izquierda, derecha)
indice := 0
max := 0
para j := (izquierda + 1) hasta (derecha - 1) hacer
d := distancia del punto vector[j] a la recta (vector[izquierda], vector[derecha])
si (d > max) entonces
max := d
indice := j
fin si
fin para
si (max > epsilon) entonces
ramer_douglas_peucker(vector, epsilon, izquierda, indice)
ramer_douglas_peucker(vector, epsilon, indice, derecha)
en otro caso
para j := (izquierda + 1) hasta (derecha - 1) hacer
marcar vector[j] como descartado de la ruta final
fin para
fin si
Y un ejemplo de implementación en C++ utilizando plantillas:
#include <vector> extern "C++" { namespace avelino { using namespace std; class RamerDouglasPeuckerPoint { public: virtual double getRamerDouglasPeuckerDistance(RamerDouglasPeuckerPoint &p1, RamerDouglasPeuckerPoint &p2) = 0; virtual void markAsDiscarded() = 0; }; template <class T> void ramerDouglasPeuckerSimplify(vector<T> &v, double epsilon, int left, int right) { // find the point with the max distance int index = 0; double maxDistance = 0; for (int j = left + 1; j <= (right - 1); j++) { RamerDouglasPeuckerPoint *p = &v[j]; double d = p->getRamerDouglasPeuckerDistance(v[left], v[right]); if (d > maxDistance) { index = j; maxDistance = d; } } if (maxDistance > epsilon) { // recursive calls ramerDouglasPeuckerSimplify(v, epsilon, left, index); ramerDouglasPeuckerSimplify(v, epsilon, index, right); } else { // discard all but first and last point for (int j = left + 1; j <= (right - 1); j++) v[j].markAsDiscarded(); } } } }
Para utilizar la función template hay que crear una clase que herede de
RamerDouglasPeuckerPoint y que implemente, al menos, los dos métodos virtuales puros. Para puntos en el plano 2D podríamos hacer una clase de este estilo:#include "RamerDouglasPeucker.H" extern "C++" { namespace avelino { using namespace std; class MapPoint : public RamerDouglasPeuckerPoint { protected: double x; double y; bool discarded; public: MapPoint(double x, double y); double getRamerDouglasPeuckerDistance(RamerDouglasPeuckerPoint &p1, RamerDouglasPeuckerPoint &p2); void markAsDiscarded(); double getX(); double getY(); bool isDiscarded(); }; } }
Esta clase implementaría el método
getRamerDouglasPeuckerDistance, que devuelve la distancia entre el punto y la recta formada por los dos puntos pasados por parámetros, y el método markAsDiscarded que permite marcar puntos como descartados. Utilizando esta clase, invocar el algoritmo es tan sencillo como hacer:... vector<MapPoint> v; ramerDouglasPeuckerSimplify<MapPoint>(v, 1.3, 0, v.size() - 1); ...
A continuación puede verse el resultado de la ejecución del algoritmo sobre un perfil del continente africano formado por 28653 puntos, al que se le aplica el algoritmo con $\varepsilon = 4.5$.
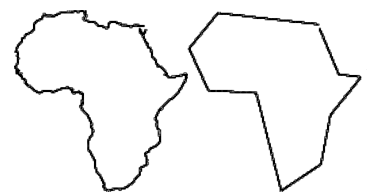
(imagen extraida de http://www.scielo.br/scielo.php?pid=S0104-65002004000100006&script=sci_arttext con licencia Creative Commons Attribution License. Sociedade Brasileira de Computação)
Código fuente en la sección soft.
[ 2 comentarios ] ( 5503 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 3891 )
( 3 / 3891 )Implementar la función exponencial en un sistema embebido con poca RAM, poca memoria de programa y sin coprocesador matemático pasa, normalmente, por intentar evitar el uso de la librería matemática de C. La sobrecarga que produciría el utilizar la función “exp” de dicha librería unida a la sobrecarga propia de la manipulación de datos en coma flotante por software desaconsejan totalmente el uso de dicha librería en sistema embebidos pequeños. Analizaremos diferentes aproximaciones polinomiales a la función exponencial y el uso de aritmética de punto fijo para realizar dicho cálculo.
Analizaremos dos aproximaciones polinómicas: La serie de Taylor y la aproximación de Padé (esta última se trata realmente de una aproximación racional).
Serie de Taylor
Lo primero que se le suele venir a uno a la cabeza cuando piensa en aproximaciones polinómicas suele ser la serie de Taylor, dicha serie es muy sencilla de calcular y genera una buena aproximación en el entorno de un punto. En este caso se ha optado por aproximar la función exponencial en el entorno de x=0:
$$e^{x} \simeq 1 + {x \over 1!} + {x^2 \over 2!} + {x^3 \over 3!} + ...$$
Esto nos da una muy buena aproximación, aunque para conseguir un error aceptable, es necesario calcular la serie de Taylor para un orden relativamente alto. El error con respecto a la función “exp” de la librería matemática de C comienza a ser asumible a partir del orden 6 trabajando en coma flotante.
Aproximación de Padé
La aproximación de Padé de orden (m, n) es la función racional:
$$R(x) = {p_0 + p_{1}x + p_{2}x^2 + ... + p_{m}x^m \over 1 + q_{1}x+ q_{2}x^2 + ... + q_{n}x^n}$$
Que cumple que:
$$f(0) = R(0)$$
$$f'(0) = R'(0)$$
$$f''(0) = R''(0)$$
$$...$$
$$f^{(m+n)}(0) = R^{(m+n)}(0)$$
El cálculo de los coeficientes de Padé no es trivial y existen varias técnicas para obtenerlos, como el algoritmo Epsilon de Wynn o el algoritmo euclídeo extendido para el cálculo del máximo común divisor. Por suerte, para la función exponencial, podemos consultar las tablas de Padé que ya se encuentran en internet calculadas para diferentes órdenes (valores de m y de n):
Aquí una tabla publicada en wikipedia.
Se ha optado en este caso por utilizar la aproximación de Padé de orden [3 / 3] (m = n = 3).
A continuación puede verse una implementación en C de ambas aproximaciones.
double taylor_exp(double x) { double ret = 0; int i; double num = 1; double den = 1; for (i = 0; i <= 6; i++) { ret += num / den; num *= x; den *= (i + 1); } return ret; } double pade_exp(double x) { double x2 = x * x; double x3 = x2 * x; double num = 1 + (x / 2) + (x2 / 10) + (x3 / 120); double den = 1 - (x / 2) + (x2 / 10) - (x3 / 120); return num / den; }
Como puede apreciarse, la serie de Taylor es de orden 6, mientras que la aproximación de Padé que se ha implementado es la de orden [3 / 3]. A continuación se reproduce la salida de una prueba de ambas funciones comparándolas con la función “exp” de la librería matemática:
# ./taylor_vs_pade_float
exp(0.250000):
exp() function : 1.2840254167
6th order taylor : 1.2840254042
3rd order pade : 1.2840254175
Como puede verse, la aproximación de Padé consigue un error comparable al de la serie de Taylor con muchas menos operaciones.
Utilizar aritmética de punto fijo
Ahora que están ambos algoritmos implementados en coma flotante, pasaremos el cálculo a aritmética de punto fijo en formato Q16.16 (más info sobre la notación Q). En el formato Q16.16 tenemos 16 bits para la parte entera y 16 bits para la parte fraccionaria, en total 32 bits.
typedef int32_t fixedpoint_t; #define FP_NEG(x) (-(x)) #define FP_ADD(x, y) ((x) + (y)) #define FP_SUB(x, y) ((x) - (y)) #define FP_MUL(x, y) ((int32_t) (((int64_t) (x)) * ((int64_t) (y)) >> 16)) #define FP_DIV(x, y) ((int32_t) ((((int64_t) (x)) << 16) / ((int64_t) (y)))) #define TO_FP(x) ((int32_t) ((x) << 16)) #define FROM_FP(x) ((x) >> 16) #define FP_FRACTIONAL_BITS 16
Las funciones anteriores puede ser ahora reescritas para utilizar el formato Q16.16:
fixedpoint_t taylor_exp(fixedpoint_t x) { fixedpoint_t ret = 0; int i; fixedpoint_t num = TO_FP(1); fixedpoint_t den = TO_FP(1); for (i = 0; i <= 6; i++) { ret = FP_ADD(ret, FP_DIV(num, den)); num = FP_MUL(num, x); den = FP_MUL(den, FP_ADD(TO_FP(i), TO_FP(1))); } return ret; } fixedpoint_t pade_exp(fixedpoint_t x) { fixedpoint_t x2 = FP_MUL(x, x); fixedpoint_t x3 = FP_MUL(x2, x); fixedpoint_t num = FP_ADD(TO_FP(1), FP_ADD(FP_DIV(x, TO_FP(2)), FP_ADD(FP_DIV(x2, TO_FP(10)), FP_DIV(x3, TO_FP(120))))); fixedpoint_t den = FP_ADD(FP_SUB(FP_DIV(x2, TO_FP(10)), FP_DIV(x3, TO_FP(120))), FP_SUB(TO_FP(1), FP_DIV(x, TO_FP(2)))); return FP_DIV(num, den); }
En este caso, realizando la misma prueba obtenemos resultados algo peores (debido a la pérdida de precisión inherente al uso del punto fijo) y, aunque para las dos aproximaciones obtenemos el mismo valor, la aproximación de Padé requiere menor cantidad de operaciones que la serie de Taylor.
# ./taylor_vs_pade_fixed
exp(0.250000):
exp() function : 1.2840254167
6th order taylor : 1.2839965820
3rd order pade : 1.2839965820
La aproximación de Padé, como ha podido verse, da mejores resultados que las series de Taylor como aproximación a la función exponencial, tanto desde el punto de vista de la eficiencia como de la precisión.
[ añadir comentario ] ( 4348 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 4058 )
( 3 / 4058 )
 Calendario
Calendario




