La teoría.
La fuerza que actúa sobre un punto $\vec{p}_i$ se puede definir, según la primera ley de Newton, como:
$$\vec{F}_i = m_i \vec{a}_i$$
Si despejamos la aceleración nos queda:
$$\vec{a}_i = {1 \over m_i} \vec{F}_i$$
Como la aceleración es la derivada de la velocidad con respecto al tiempo:
$${d\vec{v}_i \over dt} = {1 \over m_i} \vec{F}_i$$
Teniendo en cuenta que la fuerza total aplicada sobre el punto $\vec{p}_i$ es la suma de cada una de las fuerzas aplicadas en ese punto:
$${d\vec{v}_i \over dt} = {1 \over m_i} \sum\limits_j \vec{F}_{ij}$$
Siendo $\vec{F}_{ij}$ la fuerza aplicada en el punto $\vec{p}_i$ por parte del muelle que conecta dicho punto al punto $\vec{p}_j$. Desarrollando la ecuación anterior utilizando la ley de Hooke para el cálculo de $\vec{F}_{ij}$, obtenemos el siguiente sistema de ecuaciones diferenciales:
$${d\vec{v}_i \over dt} = {1 \over m_i} \sum\limits_j (k_{mij} \vec{e}_{ij} - k_{aij}(\vec{v}_i - \vec{v}_j))$$
$${d\vec{p}_i \over dt} = \vec{v}_i$$
Siendo:
$\vec{p}_i$ = El vector posición del punto $i$.
$\vec{v}_i$ = El vector velocidad del punto $i$ (derivada de $\vec{p}_i$ con respecto al tiempo).
$\vec{v}_j$ = El vector velocidad del punto $j$ (derivada de $\vec{p}_j$ con respecto al tiempo).
$\vec{e}_{ij}$ = El vector elongación del punto $i$ con respecto al punto $j$.
$m_i$ = La masa del punto $i$.
$k_{mij}$ = La constante del muelle que une los puntos $i$ y $j$.
$k_{aij}$ = La constante del amortiguador que une los puntos $i$ y $j$.
En esta ecuación, $k_{mij} \vec{e}_{ij}$ es la fuerza del muelle puro y $k_{aij}(\vec{v}_i - \vec{v}_j)$ es la fuerza del amortiguador.
El vector de elongación $\vec{e}_{ij}$ se calcula de la siguiente manera:
Siendo $l_{rij}$ la longitud, en reposo, del muelle que une los puntos $\vec{p}_i$ y $\vec{p}_j$.
Si $Distancia(\vec{p}_i, \vec{p}_j) < l_{rij}$, entonces $\vec{e}_{ij}$ es el vector unitario que va de $\vec{p}_j$ a $\vec{p}_i$.
Si $Distancia(\vec{p}_i, \vec{p}_j) > l_{rij}$, entonces $\vec{e}_{ij}$ es el vector unitario que va de $\vec{p}_i$ a $\vec{p}_j$.
Si $Distancia(\vec{p}_i, \vec{p}_j) = l_{rij}$, entonces $\vec{e}_{ij} = (0, 0)$.
El sumatorio debe recorrer todos los $j$ que representen puntos unidos al punto $i$ mediante un muelle.
Para implementar las ecuaciones diferenciales se puede aplicar el método de Euler (tiene un buen comportamiento para intervalos de $t$ pequeños y constantes y es múy fácil de programar aunque el error es un poco alto). Lo que se suele recomendar en foros de programación es el método de Runge-Kutta de cuarto orden: no es complicado de implementar y tiene un error razonablemente bajo.
Implementación mediante el método de Euler.
Para una ecuación diferencial de la siguiente forma:
$${dy \over dt} = f(t, y)$$
Podemos aproximar de forma numérica la integral resultante:
$$y=\int f(t, y)dt$$
mediante la siguiente ecuación de recurrencia:
$$y_{n+1} = y_n + hf(t_n, y_n)$$
Siendo $h$ el ancho del intervalo de integración en el tiempo (cuando más chico mejor). Si integramos el sistema de ecuaciones diferenciales del sistema de puntos unidos por muelles:
$$\vec{v}_i = \int {1 \over m_i} \sum\limits_j (k_{mij} \vec{e}_{ij} - k_{aij}(\vec{v}_i - \vec{v}_j))dt$$
$$\vec{p}_i = \int \vec{v}_i dt$$
podemos aplicar el método de Euler de forma directa:
$$\vec{v}_i[n+1] = \vec{v}_i[n] + h{1 \over m_{i}} \sum\limits_j (k_{mij}\vec{e}_{ij}[n] - k_{aij}(\vec{v}_i[n] - \vec{v}_j[n]))$$
$$\vec{p}_i[n+1] = \vec{p}_i[n] + h \vec{v}_i[n]$$
$h$ es el ancho en segundos de cada intervalo de simulación. Esta $h$ se puede calcular de la siguiente manera:
$$h = {1 \over fps}$$
Siendo $fps$ la tasa de refresco en frames por segundo.
En esta web he implementado en javascript y HTML5 un pequeño sistema de cuatro masas unidas por muelles. Haciendo click con el ratón se pueden mover las masas e interactuar con el sistema.
[ añadir comentario ] ( 2485 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 3650 )
( 3 / 3650 )La empresa japonesa de decoración Gurgle Co., Ltd. ha usado un tema mío como música de fondo en un vídeo promocional :-).
[ añadir comentario ] ( 2220 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 3827 )
( 3 / 3827 )El uso de la memoria compartida en sistemas operativos compatibles SystemV y BSD (como Linux, FreeBSD, OSX, etc.) siempre ha estado tradicionalmente asociado al uso del lenguaje C. Sin embargo, si estamos en C++, podemos utilizar la memoria compartida sin renunciar al paradigma de la orientación a objetos: Creando objetos en dicha memoria compartida. Estos “objetos compartidos” serán accesibles, al estar alojados en memoria compartida, desde todos los procesos que tengan acceso a ella.
El truco consiste simplemente en redefinir el operador “new” para la clase de los objetos que queremos compartir:
extern "C++" { using namespace std; namespace avelino { class TShared { private: int a; public: TShared(); void setA(int v); int getA(); static void *memArea; void *operator new (unsigned int size); }; } } ... void *TShared::operator new (unsigned int size) { return TShared::memArea; }
Como se puede observar, hacemos que
new TShared() devuelva un puntero a un área de memoria controlada por nosotros (no estoy implementando el delete ni estoy realizando una gestión de memoria como tal: obsérvese que dos new TShared() seguidos devolverían la misma posición de memoria, estoy haciéndolo así para facilitar la comprensión).Bueno, ya tenemos una clase que, al hacerle
new nos va a devolver un puntero a una dirección de memoria controlada por nosotros. Ahora sólo nos queda inicializar dicho puntero adecuadamente.Debe haber un proceso que cree el objeto en memoria compartida:
int shmid = shmget(SHM_KEY, sizeof(TShared), IPC_CREAT | IPC_EXCL | 0700); TShared::memArea = shmat(shmid, NULL, 0); TShared *p = new TShared(); p->setA(12345);
Como se puede ver, antes de hacer el
new TShared() inicializo TShared::memArea con la zona de memoria compartida que acabo de crear (he omitido, por claridad, los if que controlan los posibles errores que puedan devolver la funciones shmget, shmat, etc.). Ahora nuestro objeto de tipo TShared está en la memoria compartida identificada por SHM_KEY (una constante cualquiera definida por nosotros y mayor que cero).Si otro proceso quiere acceder a dicho “objeto compartido” sólo tendrá que acceder a dicha memoria compartida y hacer el cast correspondiente:
int shmid = shmget(SHM_KEY, sizeof(TShared), 0700); TShared::memArea = shmat(shmid, NULL, 0); TShared *p = (TShared *) TShared::memArea; cout << "a = " << p->getA() << endl;
El código fuente completo lo he puesto en la sección soft de la web.
[ 2 comentarios ] ( 8497 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 3841 )
( 3 / 3841 )Versión iniciar y muy básica de un minisintetizador mononfónico de onda cuadrada con entrada MIDI y basado en Arduino. Por ahora sólo reconoce mensajes MIDI "NOTE ON" y "NOTE OFF".
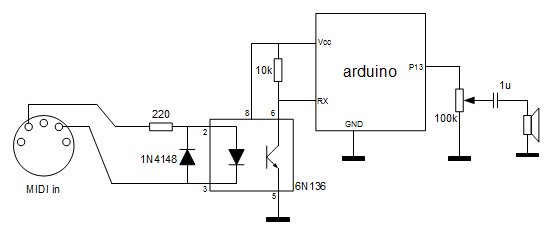
El procesador del Arduino se encarga simplemente de parsear los mensajes MIDI: Genera los tonos y los silencios ante las tramas NOTE ON y NOTE OFF que detecta por la entrada MIDI.
#define MIDI_NOTE_LOW 16
#define MIDI_NOTE_HIGH 107
// midi frequencies from C0 to B7
int freq[] = {
21, 22, 23, 24, 26, 28, 29, 31,
33, 35, 37, 39, 41, 44, 46, 48, 52, 55, 58, 62,
65, 69, 73, 78, 82, 87, 92, 98, 104, 110, 117, 123,
131, 139, 147, 156, 165, 175, 185, 196, 208, 220, 233, 247,
262, 277, 294, 311, 329, 349, 370, 392, 415, 440, 466, 494,
523, 554, 587, 622, 659, 698, 740, 784, 831, 880, 932, 988,
1047, 1109, 1175, 1245, 1319, 1397, 1480, 1568, 1661, 1760, 1864, 1976,
2093, 2217, 2349, 2489, 2637, 2794, 2960, 3136, 3322, 3520, 3729, 3951
};
#define MIDI_STATUS_WAIT_STATUS 0
#define MIDI_STATUS_WAIT_NOTE 1
#define MIDI_STATUS_WAIT_VELOCITY 2
#define MIDI_STATUS_WAIT_NOTE_OR_STATUS 3
#define SPEAKER_PIN 13
int midiStatus = MIDI_STATUS_WAIT_STATUS;
int midiNote = 0;
int midiVelocity = 0;
void setup() {
Serial1.begin(31250);
}
void parseMidi(int b) {
if (midiStatus == MIDI_STATUS_WAIT_STATUS) {
if ((b & 0xF0) == 0x90)
midiStatus = MIDI_STATUS_WAIT_NOTE;
}
else if (midiStatus == MIDI_STATUS_WAIT_NOTE) {
midiNote = b;
midiStatus = MIDI_STATUS_WAIT_VELOCITY;
}
else if (midiStatus == MIDI_STATUS_WAIT_VELOCITY) {
midiVelocity = b;
midiStatus = MIDI_STATUS_WAIT_STATUS;
if (midiVelocity == 0)
noTone(SPEAKER_PIN);
else {
if ((midiNote >= MIDI_NOTE_LOW) && (midiNote <= MIDI_NOTE_HIGH))
tone(SPEAKER_PIN, freq[midiNote - MIDI_NOTE_LOW]);
}
midiStatus = MIDI_STATUS_WAIT_NOTE_OR_STATUS;
}
else if (midiStatus == MIDI_STATUS_WAIT_NOTE_OR_STATUS) {
if (b < 0x80) {
midiNote = b;
midiStatus = MIDI_STATUS_WAIT_VELOCITY;
}
else if ((b & 0xF0) == 0x90)
midiStatus = MIDI_STATUS_WAIT_NOTE;
else
midiStatus = MIDI_STATUS_WAIT_STATUS;
}
}
void loop() {
while (Serial1.available() > 0) {
int b = Serial1.read();
parseMidi(b);
}
}
Como se puede ver, el parseado de las tramas MIDI se realiza mediante un sencillo autómata finito (DFA) de 4 estados.
[ añadir comentario ] ( 2652 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 5795 )
( 3 / 5795 )Esta vez la usuaria TheBabyride de youtube ha musicalizado uno de sus famosos vídeos sobre manicura con un tema mío.
[ añadir comentario ] ( 2430 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 3795 )
( 3 / 3795 )
 Calendario
Calendario




