El circuito
La interfaz de un display LCD estándar de caracteres es una interfaz paralelo de 8 bits, con 3 líneas de control adicionales (RS, EN y RW). Del bus paralelo de 8 bits pueden usarse sólo los 4 bits más significativos enviando de forma adecuada los comandos. Los circuitos de conversión a I2C que se venden habitualmente por AliExpress, Ebay y demás están basados en el conversor I2C/paralelo de 8 bits PCF8574 de Texas Instruments: del bus paralelo de dicho conversor se sacan los 4 bits más significativos para el bus paralelo del LCD y las tres señales de control para RS, EN y RW.
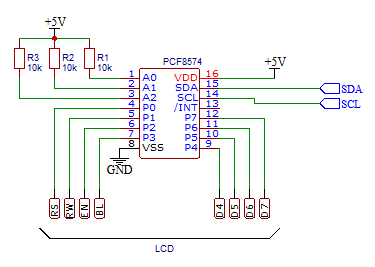
La configuración habitual en este tipo de módulos es esta:
| PCF8574 | bit 7 | bit 6 | bit 5 | bit 4 | bit 3 | bit 2 | bit 1 | bit 0 |
| LCD | D7 | D6 | D5 | D4 | BL | EN | RW | RS |
En la tabla se puede apreciar una cuarta señal de control etiquetada como BL (backlight) que controla el encendido del led de la luz trasera. Dicho led no forma parte de la circuitería estándar del display y ha sido introducido en versiones más recientes.
El problema
Los displays baratos de caracteres LCD que se encuentran en el mercado están basados en en un chip de Hitachi que no se caracteriza precisamente por su velocidad (probablemente debe ser uno de los chips más rentabilizados de toda la historia de Hitachi) y normalmente cada acceso debe estar seguido por una espera de uno a varios microsegundos, dependiendo del acceso realizado. A continuación puede verse la tabla de comandos de referencia del display, nótese la columna de la derecha ("Execution Time"):
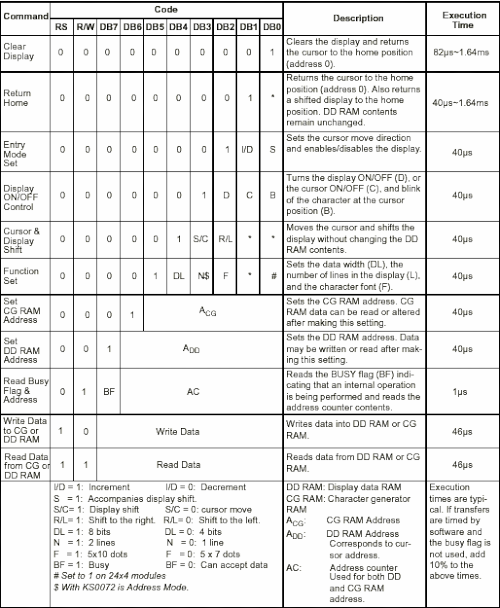
(imagen extraida de https://learningmsp430.wordpress.com/2013/11/13/16x2-lcd-interfacing-in-8bit-mode/)
Cuando uno realiza una búsqueda en internet sobre códigos de ejemplo para control de displays LCD, la gran mayoría de los mismos (no digo todos porque considero que no los he visto todos, pero al menos todos los que yo he visto), implementan las esperas mediante retardos utilizando funciones "delay" o similares. Esta forma de implementación, aunque resulta simple, supone un desperdicio de ciclos e impide que el microcontrolador realice otras tareas de forma concurrente.
La solución no bloqueante
La solución ideal pasaría por una implementación basada en colas y en interrupciones. En este caso se ha implementado una máquina de estados que controla el flujo de datos I2C, el troceado de los bytes en dos nibbles y las esperas que hay que realizar entre un envío y el siguiente. Grosso modo, la solución sería la siguiente:
- Cada vez que se quiere escribir en el display, lo que se hace es escribir lo que se quiere mandar al display en una cola de datos, por lo que la función encargada de escribir regresa inmediatamente (no es bloqueante).
- El systick del microcontrolador cuando detecta que hay algún dato en la cola de datos inicia una máquina de estados que se encarga de trocear en byte en dos nibbles y enviarlos en tiempos diferentes, así hasta que la cola de datos quede vacía, en cuyo momento la máquina de estados pasa a modo "IDLE" y queda a la espera que de haya más datos en la cola.
- La capa I2C también está implementada como una cola de bytes de tal manera que si la capa LCD quiere escribir N bytes seguidos por I2C, los escribe de forma no bloqueante en la cola I2C (la función de escritura I2C también regresa inmediatamente) y se va vaciando a medida que la interrupción de callback de transmisión es llamada por el microcontrolador.
A continuación puede verse cómo ha quedado la máquina de estados del controlador LCD:
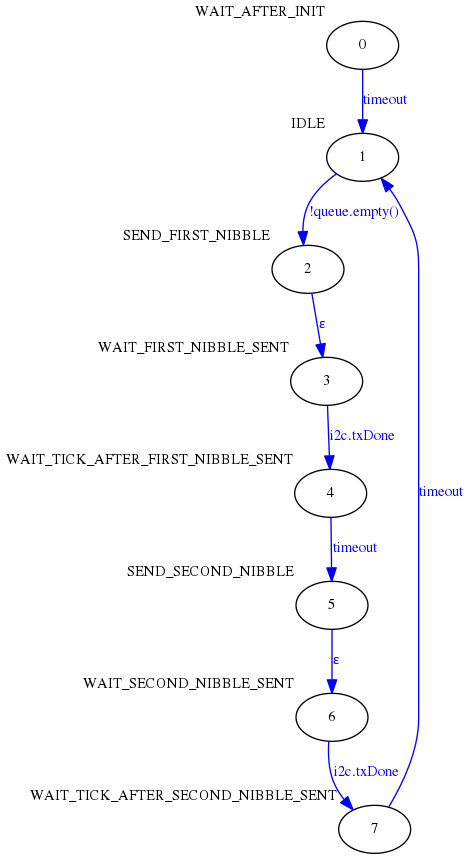
El código no queda tan sencillo a simple vista pero se trata, sin duda, de una implementación más eficiente.
#include "LCD.H" using namespace avelino; using namespace std; void LCD::init(uint8_t address) { this->address = address; this->timerCounter = 5; this->status = LCD::Status::WAIT_AFTER_INIT; this->queue.push(LCD::QueueItem(0x33, LCD::IsCommand::YES)); this->queue.push(LCD::QueueItem(0x32, LCD::IsCommand::YES)); this->queue.push(LCD::QueueItem(0x28, LCD::IsCommand::YES)); this->queue.push(LCD::QueueItem(0x08, LCD::IsCommand::YES)); this->queue.push(LCD::QueueItem(0x01, LCD::IsCommand::YES)); this->queue.push(LCD::QueueItem(0x06, LCD::IsCommand::YES)); this->queue.push(LCD::QueueItem(0x0C, LCD::IsCommand::YES)); } void LCD::tick() { Status localStatus = this->status; do { this->status = localStatus; if (localStatus == LCD::Status::WAIT_AFTER_INIT) { if (this->timerCounter > 0) this->timerCounter--; else localStatus = LCD::Status::IDLE; } else if (localStatus == LCD::Status::IDLE) { if (!this->queue.empty()) { I2CManager::deviceAddress = this->address << 1; localStatus = LCD::Status::SEND_FIRST_NIBBLE; } } else if (localStatus == LCD::Status::SEND_FIRST_NIBBLE) { uint8_t byte = this->queue.head().byte; LCD::IsCommand isCommand = this->queue.head().isCommand; I2CManager::txQueue.push((byte & 0xF0) | ((isCommand == LCD::IsCommand::YES) ? LCD::RS_0 : LCD::RS_1) | LCD::RW_0 | LCD::EN_1 | LCD::BL_1); I2CManager::txQueue.push((byte & 0xF0) | ((isCommand == LCD::IsCommand::YES) ? LCD::RS_0 : LCD::RS_1) | LCD::RW_0 | LCD::EN_0 | LCD::BL_1); I2CManager::send(); localStatus = LCD::Status::WAIT_FIRST_NIBBLE_SENT; } else if (localStatus == LCD::Status::WAIT_FIRST_NIBBLE_SENT) { if (I2CManager::txDone) { this->timerCounter = 1; localStatus = LCD::Status::WAIT_TICK_AFTER_FIRST_NIBBLE_SENT; } } else if (localStatus == LCD::Status::WAIT_TICK_AFTER_FIRST_NIBBLE_SENT) { if (this->timerCounter > 0) this->timerCounter--; else localStatus = LCD::Status::SEND_SECOND_NIBBLE; } else if (localStatus == LCD::Status::SEND_SECOND_NIBBLE) { uint8_t byte = this->queue.head().byte << 4; LCD::IsCommand isCommand = this->queue.head().isCommand; this->queue.pop(); I2CManager::txQueue.push((byte & 0xF0) | ((isCommand == LCD::IsCommand::YES) ? LCD::RS_0 : LCD::RS_1) | LCD::RW_0 | LCD::EN_1 | LCD::BL_1); I2CManager::txQueue.push((byte & 0xF0) | ((isCommand == LCD::IsCommand::YES) ? LCD::RS_0 : LCD::RS_1) | LCD::RW_0 | LCD::EN_0 | LCD::BL_1); I2CManager::send(); localStatus = LCD::Status::WAIT_SECOND_NIBBLE_SENT; } else if (localStatus == LCD::Status::WAIT_SECOND_NIBBLE_SENT) { if (I2CManager::txDone) { this->timerCounter = 1; localStatus = LCD::Status::WAIT_TICK_AFTER_SECOND_NIBBLE_SENT; } } else if (localStatus == LCD::Status::WAIT_TICK_AFTER_SECOND_NIBBLE_SENT) { if (this->timerCounter > 0) this->timerCounter--; else localStatus = LCD::Status::IDLE; } } while (localStatus != this->status); } void LCD::write(const char *s, int16_t size, LCD::IsCommand isCommand) { while ((*s != 0) && ((size < 0) || (size > 0))) { this->queue.push(QueueItem(*s, isCommand)); s++; if (size > 0) size--; } }
La función miembro "tick" es invocada desde la interrupción systick del microcontrolador en "main.cc":
LCD lcd; void systick() __attribute__ ((section(".systick"))); void systick() { lcd.tick(); }
Nótese que las colas (tanto la cola I2C como la cola LCD) están implementadas usando colas circulares estáticas a través de una plantilla ("StaticQueue.H").
#ifndef __STATICQUEUE_H__ #define __STATICQUEUE_H__ #include <stdint.h> extern "C++" { namespace avelino { using namespace std; template <typename T, int32_t N> class StaticQueue { public: T data[N]; int32_t headIndex; int32_t tailIndex; void push(const T &v); const T &head() { return this->data[this->headIndex]; }; void pop(); bool empty() { return (this->headIndex == this->tailIndex); }; StaticQueue() : headIndex(0), tailIndex(0) { }; }; template <typename T, int32_t N> void StaticQueue<T, N>::push(const T &v) { this->data[this->tailIndex] = v; this->tailIndex++; if (this->tailIndex == N) this->tailIndex = 0; } template <typename T, int32_t N> void StaticQueue<T, N>::pop() { this->headIndex++; if (this->headIndex == N) this->headIndex = 0; } } } #endif // __STATICQUEUE_H__
Se ha utilizado en varios sitios el "enum class", que permite trabajar con enumerados fuertemente tipados (introducido en el estándar C++11).
En la sección soft puede descargarse todo el código fuente.
[ añadir comentario ] ( 2606 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 12949 )
( 3 / 12949 )En esta primera entrega del podcast he entrevistado a Bartolomé Almeida, un ingeniero de telecomunicaciones que se ha especializado en el estándar LoRa. Nos ha hablado de las diferentes aplicaciones, módulos y librerías disponibles para empezar en el mundo de las comunicaciones a larga distancia usando este estándar.
El episodio 1 está disponible aquí.
La música utilizada es de The Underscore Orkestra. Licencia Creative Commons con atribución.
[ añadir comentario ] ( 2136 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 13428 )
( 3 / 13428 )Me he estrenado en esto de los podcasts y he decidido empezar a hacer un podcast en español sobre microcontroladores, sistemas embebidos y desarrollo de sistemas digitales.

El episodio 0 está disponible aquí.
La música utilizada es de The Underscore Orkestra. Licencia Creative Commons con atribución.
[ 1 comentario ] ( 2153 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 13767 )
( 3 / 13767 )Un año más, decorando el belén con nuevos inventos. En esta ocasión he vuelto a los orígenes y he implementado una luz, pero esta vez una luz especial que simule un fuego encendido utilizando un CPLD.
Introducción
A la hora de simular el crepitar de una llamas se ha optado por hacer que un led varíe de luminosidad de forma aleatoria varias veces por segundo.
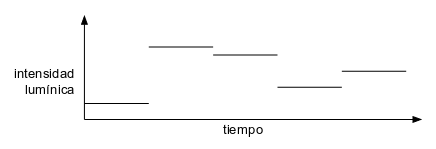
Con una luz que varíe su intensidad lumínica varias veces por segundo (entre 5 y 6 veces por segundo, por ejemplo) más una buena escenografía (color de la luz, decorados, etc.) se consigue un razonable efecto de fuego encendido.
Diseño técnico
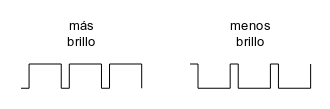
Como vamos a hacer el diseño utilizando un circuito totalmente digital, la intensidad lumínica se modulará utilizando una señal cuadrada modulada en anchura (PWM). Cuanto mayor sea el semiciclo a 1 y menor el semiciclo a 0 más brillará el led y a la inversa: cuanto mayor sea el semiciclo a 0 y menor el semiciclo a 1 menos brillará.
Si hacemos que la frecuencia sea lo suficientemente alta no se apreciará ningún tipo de parpadeo y la luz se percibirá como que brilla de forma continuada pero con diferente intensidad. El CPLD utilizado tiene conectado un reloj a 50 MHz, por tanto usando un contador de 10 bits estándar conseguiremos un desbordamiento a una frecuencia de
$${50000000 \over {2^{10}}} = 48828.125 Hz$$
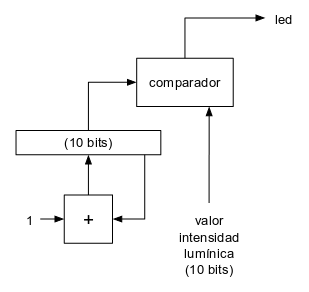
Si el valor de este contador lo comparamos con un valor determinado, el resultado de esta comparación será la salida PWM que necesitamos para el led de nuestra fogata:
El valor de intensidad lo generaremos mediante un LFSR maximal de 10 bits. Dicho LFSR ha sido utilizado en otros montajes anteriores:
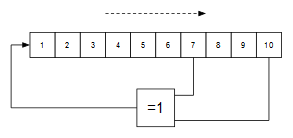
Genera una secuencia maximal de 1023 valores pseudoaleatorios (el valor 0 no aparece en la secuencia) que se puede usar como valor de intensidad lumínica:
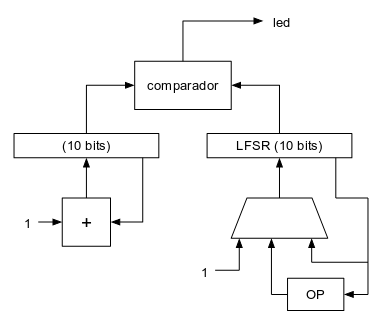
En este circuito el bloque combinacional "OP" es el que implementa el polinomio maximal de 10 bits. A continuación sólo falta implementar la temporización. Como queremos el que valor de intensidad lumínica cambie unas 5 ó 6 veces por segundo, bastará con poner un contador estándar de:
$$\lceil log_2\left({50000000 \over 6}\right) \rceil = 23 bits$$
Con un contador de 23 bits a 50 MHz tendremos una frecuencia de desbordamiento de casi 6 veces por segundo:
$${50000000 \over {2^{23}}} = 5.96 Hz$$
A continuación puede verse cómo quedaría el diagrama completo:
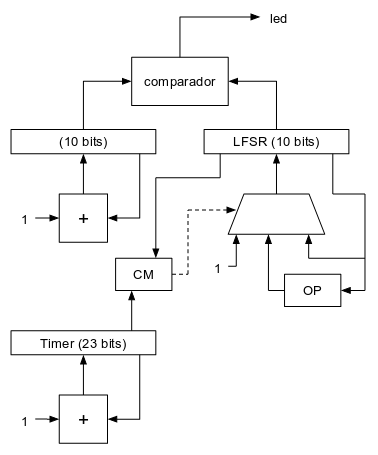
El bloque combinacional "CM" (Control del Multiplexor) se encarga de controlar la selección del multiplexor del LFSR en función del timer contador de 23 bits y del valor del propio LFSR. La tabla de verdad de este bloque sería la siguiente:
| Entradas | Salidas | |
|---|---|---|
| Timer == 0 | LFSR == 0 | MUX |
| X | 1 | "1" |
| 1 | 0 | Salida de OP |
| 0 | 0 | Salida del LFSR |
Cuando el valor del LFSR es 0, lo que hace es seleccionarla entrada "1" del multiplexor para que el LFSR se cargue con un valor distinto de cero (el 1) y poder así arrancar la generación de números aleatorios. Cuando el timer (contador de 23 bits) se desborda (pasa por cero) el LFSR se carga con el siguiente valor de la secuencia de números pseudoaleatorios y el resto del tiempo (valor del contador de 23 bits diferente de 0) el registro LFSR permanece inalterado.
Como se puede apreciar, se ha prescindido de circuitería de reset. Teniendo en cuenta que el objetivo es minimizar la circuitería y que los fabricantes siempre te garantizan que en el arranque, todos los biestables están a 0, se puede "abusar" de esta característica y ahorrar así parte de la circuitería de reset.
Posibles mejoras
Como se puede apreciar, del contador que hace de timer (el de 23 bits) sólo nos interesa cuando pasa por un valor concreto (el 0), no es como el contador que se utiliza para comparar con el LFSR y generar la señal PWM. Teniendo esto presente, dicho contador de 23 bits podría implementarse utilizando también un LFSR maximal de 23 bits: en lugar de un sumador, se puede implementar un bloque combinacionar consistente tan solo en una única puerta xor (ver polinomio a aplicar aquí), lo que supone un ahorro considerable en circuitería.
Hay que tener presente que los LFSRs no pasan nunca por cero, por lo que habría que elegir cualquier otro valor (cualquiera) como valor de "desbordamiento" (el valor 1, por ejemplo).
Implementación
A continuación puede verse la implementación de este diseño en VHDL.
library ieee; use ieee.std_logic_1164.all; use ieee.numeric_std.all; entity ChristmasFire is port ( Clk : in std_logic; Led : out std_logic ); end entity; architecture RTL of ChristmasFire is signal CounterDBus : std_logic_vector(9 downto 0); signal CounterQBus : std_logic_vector(9 downto 0); signal LFSRDBus : std_logic_vector(9 downto 0); signal LFSRQBus : std_logic_vector(9 downto 0); signal TimerDBus : std_logic_vector(22 downto 0); signal TimerQBus : std_logic_vector(22 downto 0); signal TimerOverflow : std_logic; begin -- pwm counter process (Clk) begin if (Clk'event and (Clk = '1')) then CounterQBus <= CounterDBus; end if; end process; CounterDBus <= std_logic_vector(signed(CounterQBus) + to_signed(1, 10)); -- lfsr process (Clk) begin if (Clk'event and (Clk = '1')) then LFSRQBus <= LFSRDBus; end if; end process; LFSRDBus <= std_logic_vector(to_signed(1, 10)) when (signed(LFSRQBus) = to_signed(0, 10)) else ((LFSRQBus(3) xor LFSRQBus(0)) & LFSRQBus(9 downto 1)) when (TimerOverflow = '1') else LFSRQBus; -- timer process (Clk) begin if (Clk'event and (Clk = '1')) then TimerQBus <= TimerDBus; end if; end process; TimerDBus <= std_logic_vector(signed(TimerQBus) + to_signed(1, 23)); TimerOverflow <= '1' when (signed(TimerQBus) = to_signed(0, 23)) else '0'; -- output Led <= '1' when (signed(CounterQBus) > signed(LFSRQBus)) else '0'; end architecture;
Se trata de un único fichero que puede descargarse desde la sección soft.
¡Feliz Navidad a todos!
[ añadir comentario ] ( 2102 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 11163 )
( 3 / 11163 )Partiendo del montaje realizado en el post anterior, se han realizado varias modificaciones y mejoras. El parser MIDI de esta segunda iteración genera ahora 3 señales de control, de 7 bits cada una, que se utilizan para controlar la frecuencia de corte, la resonancia y la ganancia de la entrada de un filtro paso bajo de segundo orden:
Este sería el diagrama de bloques de esta segunda iteración:
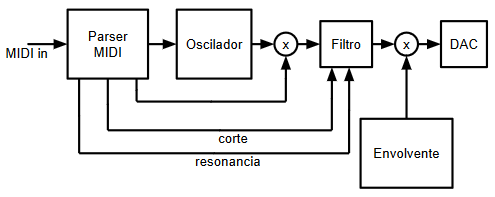
Parser MIDI mejorado
En la versión iniciar el parser MIDI no se tuvieron en cuenta algunas características "raras" que se dan el algunos teclados controladores y al mismo tiempo se asumía que un "note off" posterior a un "note on" siempre era de la misma tecla, lo cual es demasiado suponer, sobre todo cuando quien toca es un humano. Cuando un humano toca una secuencia de notas en un teclado (por ejemplo: La, Mi, Do) uno puede pensar que los mensaje que manda el teclado controlador son los siguientes:
noteOn(La), noteOff(La), noteOn(Mi), noteOff(Mi), noteOn(Do), noteOff(Do)
Sin embargo lo cierto es que a veces un humano pulsa la siguiente tecla al mismo tiempo o antes de soltar la anterior:
noteOn(La), noteOn(Mi), noteOff(La), noteOff(Mi), noteOn(Do), noteOff(Do)
Con la anterior versión del parser, que asumía que un noteOff se correspondía siempre con el noteOn inmediatamente anterior, lo que ocurría era que cuando al sinte le llegaba el noteOff(La) callaba la nota Mi disparada justo antes porque asumía que ese noteOff se correspondía con dicha nota Mi. En la nueva versión del parse este noteOff(Mi) es ignorado por la máquina de estados por lo que la respuesta del sintetizador es más natural.
Para mejorar el comportamiento y la funcionalidad del parser MIDI se ha optado por un diseño basado en máquinas de estado en serie y en paralelo en lugar de una única máquina de estados grande. El parser MIDI se ha divido en dos etapas (Stage1 y Stage2), la primera etapa genera señales "KeyOn" y "KeyOff" limpias por cables separados y además implementa en paralelo una máquina de estados aparte para procesar los mensajes de "Control Change". En la segunda etapa se implementa la lógica anteriormente descrita de ignorar los "Note Off" que no se corresponden con el mensaje "Note On" inmediatamente anterior.
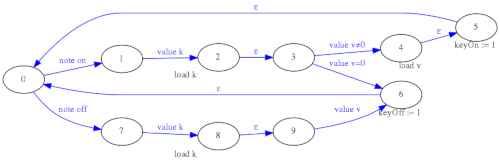
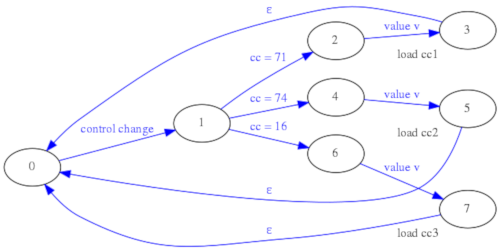
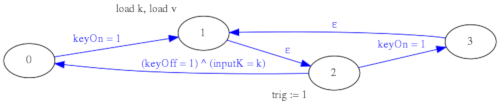
De esta forma, aunque aparentemente se ha complicado el diseño, se han separado los problemas y es más sencillo introducir modificaciones y depurar errores en las máquinas de estado. Cada una por separado es más sencilla y fácil de trazar que una hipotética máquina de estados única para todo.
Además de la mejora en el procesado de los mensajes "Note On" y "Note Off", este parser ya reconoce mensajes de tipo "Control Change", en concreto para tres valores prefijados de controlador: 71, 74 y 16, que se asignarán en el sintetizador a la frecuencia de corte del filtro, la resonancia del filtro y la ganancia de entrada del filtro.
Filtro paso bajo de segundo orden
Se ha optado por la implementación estándar de un filtro de estado variable (state variable filter). Se trata de un filtro de segundo orden (dos polos) que genera simultáneamente 3 salidas:
- paso bajo (con pendiente de filtrado de 12 dB/octava)
- paso alto (con pendiente de filtrado de 12 dB/octava)
- paso banda (con pendiente de filtrado de 6 dB/octava)
No son grandes pendientes de filtrado pero siempre se pueden mejorar poniendo varios filtros en cascada. La implementación que se ha utilizado es la descrita en el libro "Musical Applications of Microprocessors" de Hal Chamberlin (dicha implementación ya fue usada sobre un microcontrolador en este post). El filtro de estado variable viene determinado por el siguiente sistema de ecuaciones en diferencias finitas:
$$pasoAlto[n] = entrada - ({r \times pasoBanda[n-1]}) - pasoBajo[n]$$
$$pasoBanda[n] = ({f \times pasoAlto[n]}) + pasoBanda[n - 1]$$
$$pasoBajo[n] = ({f \times pasoBanda[n - 1]}) + pasoBajo[n - 1]$$
Siendo:
$$f = 2\sin\left({\pi F_c \over F_s}\right)$$
$$r = {1 \over Q}$$
Siendo $F_c$ la frecuencia de corte del filtro, $F_s$ la frecuencia de muestreo y $Q$ la Q del filtro (la resonancia).
Si se reordenan las ecuaciones en diferencias:
$$pasoBajo[n] = ({f \times pasoBanda[n - 1]}) + pasoBajo[n - 1]$$
$$pasoAlto[n] = entrada - ({r \times pasoBanda[n - 1]}) - pasoBajo[n]$$
$$pasoBanda[n] = ({f \times pasoAlto[n]}) + pasoBanda[n - 1]$$
Podemos olvidarnos de los índices:
pasoBajo += f * pasoBanda
pasoAlto = entrada - (r * pasoBanda) - pasoBajo
pasoBanda += f * pasoAlto
Como se puede apreciar es preciso mantener en memoria (registro) al menos las variables pasoBajo y pasoBanda entre que se procesa una muestra y la siguiente (se trata de un filtro digital de segundo orden).
Para implementar dicho filtro sobre FPGA lo que necesitaremos serán básicamente los siguientes elementos:
- Al menos tres registros en los que almacenaremos los valores "pasoBajo", "pasoBanda" y "pasoAlto" (aunque realmente podríamos no gastar un registro para "pasoAlto", lo vamos a incluir para poder disponer de esa salida en el módulo).
- Una unidad de suma con multiplicación: Un módulo combinacional que realiza la operación: A = (B * C) + D (en muchos casos D = A, por lo que se puede ver como A += B * C)
- Una máquina de estados para controlar qué operandos y operaciones se hacen en cada momento.
Con estos elemento y teniendo en cuenta las ecuaciones anteriores, podemos hacer una propuesta de secuenciación de operaciones como sigue:
1. LP := (cutoff * BP) + LP
2. HP := (0 * x ) + IN
3. HP := (-reso * BP) + HP
4. HP := (-1 * LP) + HP
5. BP := (cutoff * HP) + BP
Cada paso requiere un único ciclo de reloj por lo que bastará con implementar una máquina de estados que, por cada muestra que llegue, pase por los 5 estados de forma secuencial para que los registros LP, BP y HP (LowPass, BandPass y HighPass) tengan los valores de salida del filtro que necesitamos. Nótese que será preciso utilizar aritmética de punto fijo y en nuestro caso se ha optado por un formato Q16.16 (16 bits de parte entera y 16 bits de parte fraccionaria).
A continuación puede verse como quedaría la implementación del filtro en VHDL:
library ieee; use ieee.std_logic_1164.all; use ieee.numeric_std.all; entity StateVariableFilter is port ( Reset : in std_logic; Clk : in std_logic; EnableIn : in std_logic; SampleIn : in std_logic_vector(15 downto 0); CutOffIn : in std_logic_vector(31 downto 0); -- 0..1 fixed point Q16.16 ResonanceIn : in std_logic_vector(31 downto 0); -- 0..1 fixed point Q16.16 SampleOut : out std_logic_vector(15 downto 0); EnableOut : out std_logic ); end entity; architecture RTL of StateVariableFilter is signal LPDBus : std_logic_vector(31 downto 0); signal LPQBus : std_logic_vector(31 downto 0); signal HPDBus : std_logic_vector(31 downto 0); signal HPQBus : std_logic_vector(31 downto 0); signal BPDBus : std_logic_vector(31 downto 0); signal BPQBus : std_logic_vector(31 downto 0); signal MultOperandA : std_logic_vector(31 downto 0); signal MultOperandB : std_logic_vector(31 downto 0); signal MultResult64 : std_logic_vector(63 downto 0); signal MultResult : std_logic_vector(31 downto 0); signal AddOperandB : std_logic_vector(31 downto 0); signal AddResult : std_logic_vector(31 downto 0); signal NegResonance : std_logic_vector(31 downto 0); signal FSMDBus : std_logic_vector(2 downto 0); signal FSMQBus : std_logic_vector(2 downto 0); begin process (Clk) begin if (Clk'event and (Clk = '1')) then LPQBus <= LPDBus; end if; end process; process (Clk) begin if (Clk'event and (Clk = '1')) then HPQBus <= HPDBus; end if; end process; process (Clk) begin if (Clk'event and (Clk = '1')) then BPQBus <= BPDBus; end if; end process; process (Clk) begin if (Clk'event and (Clk = '1')) then FSMQBus <= FSMDBus; end if; end process; NegResonance <= std_logic_vector(to_signed(-to_integer(signed(ResonanceIn)), 32)); MultOperandA <= CutOffIn when ((FSMQBus = "001") or (FSMQBus = "101")) else NegResonance when (FSMQBus = "011") else std_logic_vector(to_signed(-65536, 32)) when (FSMQBus = "100") else -- -65536 es -1 en notación Q16.16 std_logic_vector(to_signed(0, 32)); MultOperandB <= LPQBus when (FSMQBus = "100") else BPQBus when ((FSMQBus = "001") or (FSMQBus = "011")) else HPQBus; AddOperandB <= LPQBus when (FSMQBus = "001") else BPQBus when (FSMQBus = "101") else HPQBus when ((FSMQBus = "011") or (FSMQBus = "100")) else std_logic_vector(to_signed(to_integer(signed(SampleIn)), 32)); --MultResult64 <= std_logic_vector(to_signed(to_integer(signed(MultOperandA)) * to_integer(signed(MultOperandB)), 64)); MultResult64 <= std_logic_vector(signed(MultOperandA) * signed(MultOperandB)); MultResult <= MultResult64(47 downto 16); --AddResult <= std_logic_vector(to_signed(to_integer(signed(MultResult)) + to_integer(signed(AddOperandB)), 32)); AddResult <= std_logic_vector(signed(MultResult) + signed(AddOperandB)); LPDBus <= std_logic_vector(to_signed(0, 32)) when (Reset = '1') else AddResult when (FSMQBus = "001") else LPQBus; HPDBus <= std_logic_vector(to_signed(0, 32)) when (Reset = '1') else AddResult when ((FSMQBus = "011") or (FSMQBus = "100") or (FSMQBus = "010")) else HPQBus; BPDBus <= std_logic_vector(to_signed(0, 32)) when (Reset = '1') else AddResult when (FSMQBus = "101") else BPQBus; -- fsm -- LP += cutoff * BP -- HP = in - (resonance * BP) - LP -- BP += cutoff * HP FSMDBus <= "000" when ((Reset = '1') or (FSMQBus = "110")) else -- MultOperandA MultOperandB AddOperandB "001" when ((FSMQBus = "000") and (EnableIn = '1')) else -- LP := cutoff * BP + LP "010" when (FSMQBus = "001") else -- HP := 0 * x + IN "011" when (FSMQBus = "010") else -- HP := -reso * BP + HP "100" when (FSMQBus = "011") else -- HP := -1 * LP + HP "101" when (FSMQBus = "100") else -- BP := cutoff * HP + BP "110" when (FSMQBus = "101") else "000"; EnableOut <= '1' when (FSMQBus = "110") else '0'; SampleOut <= std_logic_vector(to_signed(-32768, 16)) when (to_integer(signed(LPQBus)) < -32768) else std_logic_vector(to_signed(32767, 16)) when (to_integer(signed(LPQBus)) > 32767) else LPQBus(15 downto 0); end architecture;
La máquina de estados espera hasta que la entrada "EnableIn" se ponga a "1", dicho evento es la señal que indica al filtro que debe realizar una iteración (i.e. calcular la siguiente muestra a partir de la entrada "SampleIn").
Todo el código está disponible en la sección soft.
[ 1 comentario ] ( 2218 visualizaciones ) | [ 0 trackbacks ] | enlace permanente |




 ( 3 / 4496 )
( 3 / 4496 )
 Calendario
Calendario




