Esquema
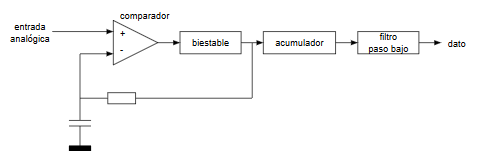
Como se puede apreciar la parte analógica del conversor se reduce a un comparador, una resistencia y un condensador. En la "zona digital" tenemos todo el meollo: un biestable, un acumulador y un filtro paso bajo. Veamos el funcionamiento con una traza sencilla.
Funcionamiento
Asumamos que empezamos con la salida que va al filtro RC a 0 y el condensador totalmente descargado y que en la entrada analógica tenemos un voltaje entre 0 y Vcc (3.3 voltios) que llamaremos $V_{in}$. En estas condiciones iniciales, como $V_{in} > 0$, el comparador emite 3.3 voltios (un 1 lógico) y por tanto, en el siguiente ciclo de reloj, el biestable carga ese 1 en su salida Q.
Tras esta primera carga la salida que va conectada al filtro RC (la Q del biestable) se pone a 1, lo que significa que el condensador empieza a cargarse a través de R. Para cuando llegue el siguiente ciclo de reloj lo más probable es que la carga del condensador aún sea muy baja y el comparador siga emitiendo a su salida un 1 (su entrada + tiene un voltaje aún mayor que su entrada -). Tendremos, por tanto que el biestable seguirá emitiendo 1s hasta que el voltaje en la entrada - del comparador sea superior a $V_{in}$, en el momento que ocurra eso la salida del comparador será de 0 voltios (un 0 lógico). El biestable en el siguiente ciclo de reloj cargará ese 0 en su Q y el condensador empezará ahora a descargarse a través de la R.
Como se puede apreciar, el sistema en lazo cerrado lo que hace es, mediante 0s y 1s tratar de hacer que el voltaje en la entrada - del comparador (el voltaje en el condensador) "siga" al voltaje de entrada $V_{in}$ y esto, en la práctica, significa que a la salida del biestable lo que tenemos es una especie de señal PWM cuyo ciclo de trabajo será proporcional al voltaje $V_{in}$:
1.- Cuanto mayor es el valor de $V_{in}$, mayor cantidad de 1s emite el biestable para tratar de "alcanzar" $V_{in}$.
2.- Cuanto menor es el valor de $V_{in}$, mayor es la cantidad de 0s que emite el biestable para tratar de "alcanzar" $V_{in}$.
3.- Se puede ver, además, que para un valor próximo a ${Vcc \over 2}$ el biestable emitirá aproximadamente la misma cantidad de 0s que de 1s por unidad de tiempo.
Ahora supongamos que pasamos la salida del biestable por un circuito combinacional que ante un 0 en la entrada emite un -1 en un bus de N bits y ante un 1 en la entrada emite un +1 en esa misma salida de N bits. Si durante $2^{N-1}$ ciclos de reloj vamos sumando en un acumulador con signo los valores +1 y -1 que van saliendo de este circuito combinacional tendremos lo siguiente:
1.- Para valores altos de $V_{in}$, que generan muchos más 1s que 0s en la salida del biestable, tendremos que el acumulador cada $2^{N-1}$ ciclos de reloj tendrá un valor próximo a $2^{N-1}$.
2.- Para valores bajos de $V_{in}$, que generan muchos más 0s que 1s en la salida del biestable, tendremos que el acumulador, cada $2^{N-1}$ ciclos de reloj, tendrá un valor próximo a $-2^{N-1}$.
3.- Para valores próximos a ${Vcc \over 2}$, que generan una cantidad muy similar de 0s y de 1s por unidad de tiempo, tendremos que el acumulador, cada $2^{N-1}$ ciclos de reloj, tendrá un valor próximo a 0.
Si cada $2^{N-1}$ ciclos de reloj cargamos el valor de este acumulador sobre un registro (que podemos llamar de salida), justo antes de poner de nuevo el acumulador a 0 (y volver a acumular los +1 y -1 que llegan del biestable), tenemos que este registro de salida será el resultado de la conversión analógico-digital del voltaje de entrada $V_{in}$ en N bits, que era nuestro objetivo. En la implementación recomendada se introduce una tercera etapa que realiza un sobremuestreo adicional para suavizar la señal (actúa como filtro paso bajo) pero que no se ha implementado en este caso por simplicidad.
Otra característica importante en este tipo de conversores es que la resolución en bits del conversor viene determinada por N (la anchura en bits del acumulador y del filtro paso bajo), que es un parámetro relativamente sencillo de cambiar, y que no requiere cambios en la electrónica externa.
Implementación
A continuación puede verse un esquema detallado de lo que sería la implementación en una FPGA o en un CPLD del conversor descrito:
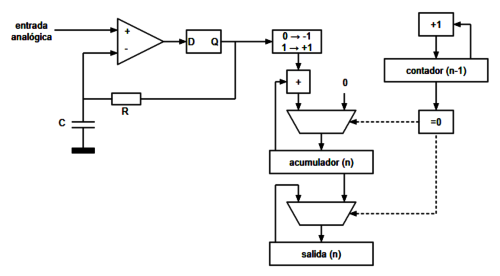
Cada vez que el contador pasa por 0 hace que en acumulador se cargue en el registro de salida y al mismo tiempo se reinicie con el valor 0. Los valores de la resistencia R y del condensador C deben ser elegidos acorde a la frecuencia de reloj del sistema. Por ejemplo, Lattice Semiconductor recomienda que la constante de tiempo del filtro $t = R \times C$ cumpla que $200 < t \times f_{clk} < 1000$. En este caso concreto se ha hecho una implementación sobre un CPLD de Altera (Intel) que va a 50 MHz y se han elegido los valores de C = 1.5 nF y R = 10 K, que cumplen dicha desigualdad.
library ieee; use ieee.std_logic_1164.all; use ieee.numeric_std.all; entity DeltaSigmaADC is port ( Reset : in std_logic; Clk : in std_logic; DataOut : out std_logic_vector(7 downto 0); ComparatorIn : in std_logic; RCChargeOut : out std_logic ); end entity; architecture Architecture1 of DeltaSigmaADC is signal DBus : std_logic; signal QBus : std_logic; signal FollowerOut : std_logic_vector(15 downto 0); signal CounterDBus : std_logic_vector(14 downto 0); signal CounterQBus : std_logic_vector(14 downto 0); signal IntegratorDBus : std_logic_vector(15 downto 0); signal IntegratorQBus : std_logic_vector(15 downto 0); signal LatchDBus : std_logic_vector(15 downto 0); signal LatchQBus : std_logic_vector(15 downto 0); begin -- biestable de seguimiento de voltaje process (Clk) begin if (Clk'event and (Clk = '1')) then QBus <= DBus; end if; end process; DBus <= ComparatorIn; RCChargeOut <= QBus; FollowerOut <= std_logic_vector(to_signed(-1, 16)) when (QBus = '0') else std_logic_vector(to_signed(1, 16)); -- contador process (Clk) begin if (Clk'event and (Clk = '1')) then CounterQBus <= CounterDBus; end if; end process; CounterDBus <= std_logic_vector(to_signed(0, 15)) when (Reset = '1') else std_logic_vector(signed(CounterQBus) + 1); -- integrador process (Clk) begin if (Clk'event and (Clk = '1')) then IntegratorQBus <= IntegratorDBus; end if; end process; IntegratorDBus <= std_logic_vector(to_signed(0, 16)) when (signed(CounterQBus) = 0) else std_logic_vector(signed(FollowerOut) + signed(IntegratorQBus)); -- latch process (Clk) begin if (Clk'event and (Clk = '1')) then LatchQBus <= LatchDBus; end if; end process; LatchDBus <= IntegratorQBus when (signed(CounterQBus) = 0) else LatchQBus; -- salida DataOut <= LatchQBus(15 downto 8); end architecture;

El código fuente está disponible en la sección soft.
Lo sentimos. No se permiten nuevos comentarios después de 90 días.

 Calendario
Calendario




