El problema
Se parte de un lazo de control estándar, el mismo que se utilizó cuando se implementó el control PID:
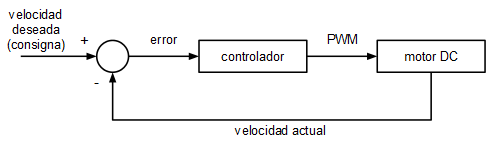
La velocidad se lee mediante un sencillo encoder compuesto por un disco pintado mitad de blanco y mitad de negro y por un sensor infrarrojo de tipo reflexivo (el CNY70, de los que suelen usarse en robots siguelineas).
El motor es accionado a través de una de las salidas PWM del microcontrolador mediante un transistor NPN de potencia.
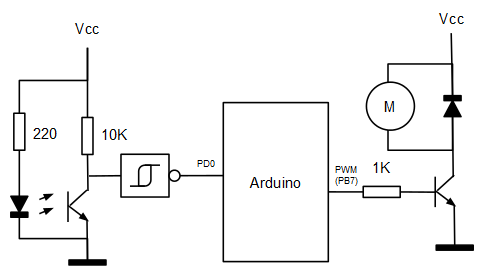
El esquema es exactamente el mismo que el utilizado en el post anterior.
Lectura de la velocidad angular
Para leer la velocidad angular se conecta la salida del sensor infrarrojo reflexivo (en concreto la salida del inversor schmitt) a una entrada de interrupción externa del microcontrolador y se programa dicha interrupción externa para que se dispare en uno de los flancos (subida o bajada, pero no en ambos a la vez). De esta forma y al estar el disco pintado mitad negro y mitad blanco, cada interrupción se corresponderá con una vuelta del eje de rotación.
float RPMReader::rpm; void RPMReader::init() { DDRD &= 0xFE; // PD0 as input cli(); EICRA = (1 << ISC01) | (1 << ISC00); // external INT0 EIMSK = (1 << INT0); sei(); Chronometer::init(); Chronometer::microseconds = 0; } void RPMReader::__isr() { uint32_t delta = Chronometer::microseconds; Chronometer::microseconds = 0; if (delta > 0) rpm = (((float) 1) / delta) * 60000000; EIFR |= (1 << INTF0); } ISR(INT0_vect) { RPMReader::__isr(); }
Cada vez que se ejecuta la interrupción (da una vuelta el eje de rotación) se obtiene la cantidad de microsegundos que han pasado desde la anterior vuelta y se calcula la velocidad angular:
uint32_t delta = Chronometer::microseconds; Chronometer::microseconds = 0; if (delta > 0) rpm = (((float) 1) / delta) * 60000000;
Señal PWM de salida
La salida del controlador borroso no es en este caso directamente el valor absoluto PWM, sino el "incremento" (o una especie de derivada) de dicho valor PWM. Esto simplifica el diseño del controlador borroso pero complica la etapa de salida, ya que hay que poner un "integrador" a la salida del controlador que convierta los incrementos PWM en valores absolutos PWM.

Afortunadamente este "integrador" no es más que un acumulador en el que se van sumando, en cada iteración, los incrementos que emite el controlador borroso. Es esta suma la que se emite como PWM para accionar el motor.
SpeedDeltaFuzzyValueWriter::SpeedDeltaFuzzyValueWriter() { this->sum = 0; } void SpeedDeltaFuzzyValueWriter::setValue(float v) { this->sum += v; if (this->sum > 255) this->sum = 255; else if (this->sum < 0) this->sum = 0; uint8_t aux = (uint8_t) this->sum; PWM::setPB7Value(aux); }
Control borroso
Para realizar el controlador se plantea como variable de entrada al mismo el error de la velocidad de rotación (deseada - actual) en revoluciones por minuto (RPM) y como variable de salida, el incremento (una especie de derivada) del ciclo de trabajo de la señal PWM que alimenta al motor DC. Se definen unos sencillos conjuntos borrosos asociados a cada una de estas dos variables:
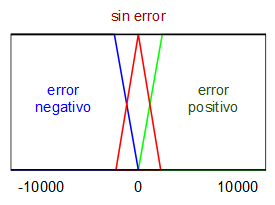
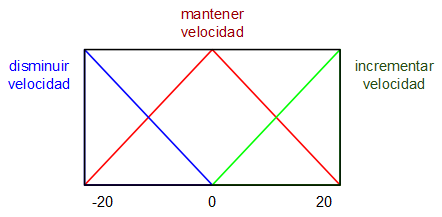
Mientras que las reglas de lógica borrosa que se van a utilizar son las siguientes:
SI (error ES error negativo) ENTONCES salida ES decrementar velocidad
SI (error ES sin error) ENTONCES salida ES mantener velocidad
SI (error ES error positivo) ENTONCES salida ES incrementar velocidad
Como puede apreciarse, las reglas son sencillas y fáciles de ajustar, de recordar y de mantener. Además, el hecho de que la variable de salida sea un incremento en lugar de un valor absoluto simplifica enormemente las reglas y los conjuntos.
Ejemplo 1
Supongamos que queremos alcanzar una velocidad de 3000 RPM y que la velocidad actual medida por el sensor de velocidad es de 2000 RPM, el error será, por tanto de 1000 RPM (consigna - valor real). Lo primero que se hace es “borrosificar” o “fuzzyficar” esta lectura:
Para la expresión “(error ES error negativo)” se calcula el grado de pertenencia de 1000 RPM al conjunto borroso “error negativo”, para la expresión “(error ES sin error)” se calcula el grado de pertenencia de 1000 RPM al conjunto borroso “sin error” y para la expresión “(error ES error positivo)” se calcula el grado de pertenencia de 1000 RPM al conjunto borroso “error positivo”:
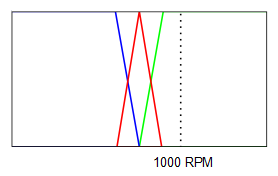
Como se puede ver:
$$\mu_{error \space negativo}(1000)=0$$
$$\mu_{sin \space error}(1000)=0$$
$$\mu_{error \space positivo}(1000)=1$$
Por lo tanto, para la salida:
$$\mu_{decrementar \space velocidad}(\Delta PWM)=0$$
$$\mu_{mantener \space velocidad}(\Delta PWM)=0$$
$$\mu_{incrementar \space velocidad}(\Delta PWM)=1$$
A continuación se calcula mediante el método de la media ponderada de centros, el valor de la salida:
$$\Delta PWM={0·C_{dec. \space velocidad}+0·C_{mant. \space velocidad}+1·C_{inc. \space velocidad} \over 0+0+1}=C_{inc. \space velocidad}=20$$
En este caso el resultado el directamente el centro del conjunto borroso “incrementar velocidad”, que vale 20, con lo que incrementamos la velocidad.
Ejemplo 2
Supongamos ahora que queremos alcanzar la misma velocidad de 3000 RPM y que la velocidad actual medida por el sensor de velocidad es de 3050 RPM, el error será, por tanto de -50 RPM (consigna - valor real). Lo primero que se hace de nuevo es “borrosificar” o “fuzzyficar” esta lectura:
Se calculan los diferentes grados de pertenencia:
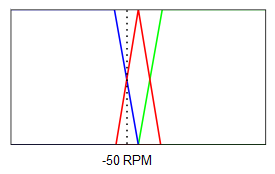
Como se puede ver:
$$\mu_{error \space negativo}(-50)=0.5$$
$$\mu_{sin \space error}(-50)=0.5$$
$$\mu_{error \space positivo}(-50)=0$$
Por lo tanto, para la salida:
$$\mu_{decrementar \space velocidad}(\Delta PWM)=0.5$$
$$\mu_{mantener \space velocidad}(\Delta PWM)=0.5$$
$$\mu_{incrementar \space velocidad}(\Delta PWM)=0$$
A continuación se calcula mediante el método de la media ponderada de centros, el valor de la salida:
$$\Delta PWM={0.5·C_{dec. \space velocidad}+0.5·C_{mant. \space velocidad}+0·C_{inc. \space velocidad} \over 0.5+0.5+0}=-10$$
Un valor de -10 en el incremento del PWM, disminuye dicho valor y, por tanto, hace que se disminuya la velocidad del motor.
En condiciones ideales, con una entrada de error de 0 RPM tendríamos:
$$\mu_{error \space negativo}(0)=0$$
$$\mu_{sin \space error}(0)=1$$
$$\mu_{error \space positivo}(0)=0$$
Por lo tanto, para la salida:
$$\mu_{decrementar \space velocidad}(\Delta PWM)=0$$
$$\mu_{mantener \space velocidad}(\Delta PWM)=1$$
$$\mu_{incrementar \space velocidad}(\Delta PWM)=0$$
Y haciendo la “desborrosificación” o “defuzzyficación” nos sale:
$$\Delta PWM={0·C_{dec. \space velocidad}+1·C_{mant. \space velocidad}+0·C_{inc. \space velocidad} \over 0+1+0}=C_{mant. \space velocidad}=0$$
Un incremento del valor PWM de 0, con lo que no cambiamos la velocidad del motor.
Para dotar al sistema de un comportamiento más estable, en los sistemas reales, suele tomarse también como entrada la derivada de la velocidad angular y establecer reglas que hagan variar el PWM en función de esta otra entrada. En este caso, por simplicidad, se ha optado por utilizar como entrada sólo la velocidad angular.
Implementación
La implementación se ha realizado en C++ y las clases definidas pueden dividirse en dos grupos: las que hacen de interfaz con hardware interno, entrada y salida (lectura del sensor de infrarrojos reflexivo para calcular la velocidad angular, salida PWM, timers, etc.) y las que forman parte del motor de inferencia borroso (expresiones, conjuntos borrosos, variables lingüísticas, reglas, etc.)
Diagrama de clases 1:
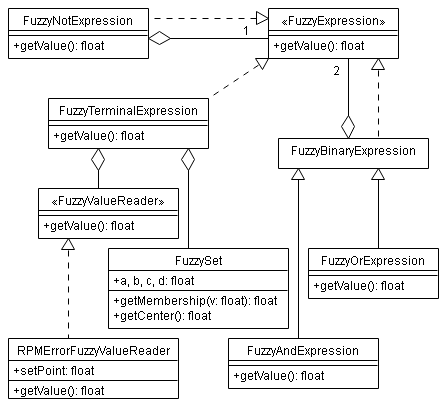
Diagrama de clases 2:
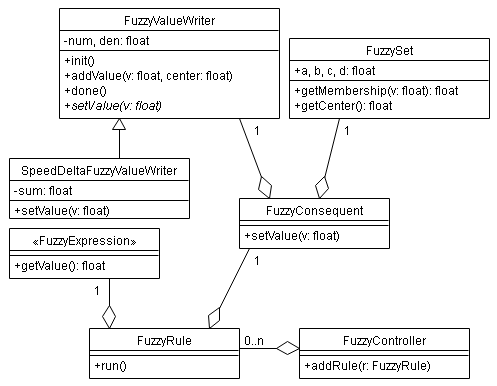
Los conjuntos borrosos (clase FuzzySet) se definen de forma trapezoidal:
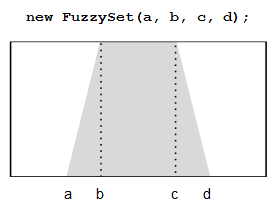
En el caso concreto que nos ocupa los conjuntos estarán, por tanto, definidos así:
FuzzySet negativeError(-10000, -10000, -100, 0); FuzzySet noError(-100, 0, 0, 100); FuzzySet positiveError(0, 100, 10000, 10000); FuzzySet decreaseSpeed(-20, -20, -20, 0); FuzzySet keepSpeed(-20, 0, 0, 20); FuzzySet increaseSpeed(0, 20, 20, 20);
Cada regla de inferencia borrosa estará definida por un antecedente (objeto de clase FuzzyExpression o derivadas) y por un consecuente (objeto de clase FuzzyConsequent).
FuzzyController c;
c.addRule(
new FuzzyTerminalExpression(entrada1, conjunto1),
new FuzzyConsequent(salida1, conjunto3)
); // SI (entrada1 ES conjunto1) ENTONCES salida1 ES conjunto3
En el antecedente podemos hacer combinaciones “Y”, “O” y “NO” utilizando las clases FuzzyAndExpression, FuzzyOrExpression y FuzzyNotExpression respectivamente.
c.addRule(
new FuzzyAndExpression(
new FuzzyTerminalExpression(entrada1, conjunto1),
new FuzzyTerminalExpression(entrada2, conjunto2)
),
new FuzzyConsequent(salida1, conjunto3)
); // SI (entrada1 ES conjunto1) Y (entrada2 ES conjunto2) ENTONCES salida1 ES conjunto3
De esta forma podemos crear reglas de inferencia borrosa tan complejas como queramos. Se ha aprovechado, además, la capacidad que tiene C++ de redefinir operadores y se han usado los operadores “&&”, “||”, “!” y “%” como sinónimos de FuzzyAndExpression, FuzzyOrExpression, FuzzyNotExpression y FuzzyTerminalExpression, respectivamente:
FuzzyExpression &avelino::operator % (FuzzyValueReader &vr, FuzzySet &fs) { FuzzyExpression *ret = FuzzyTerminalExpression::getInstance(vr, fs); return *ret; } FuzzyExpression &avelino::operator && (FuzzyExpression &e1, FuzzyExpression &e2) { FuzzyExpression *ret = FuzzyAndExpression::getInstance(e1, e2); return *ret; } FuzzyExpression &avelino::operator || (FuzzyExpression &e1, FuzzyExpression &e2) { FuzzyExpression *ret = FuzzyOrExpression::getInstance(e1, e2); return *ret; } FuzzyExpression &avelino::operator ! (FuzzyExpression &e) { FuzzyExpression *ret = FuzzyNotExpression::getInstance(e); return *ret; }
Ahora se puede escribir la regla de ejemplo de antes “SI (entrada1 ES conjunto1) Y (entrada2 ES conjunto2) ENTONCES salida 1 ES conjunto3” de la siguiente manera:
c.addRule(
(entrada1 % conjunto1) && (entrada2 % conjunto2),
new FuzzyConsequent(salida1, conjunto3)
);
Como se puede apreciar, la sintaxis se vuelve más clara y las reglas son más fáciles de leer y de mantener. En el caso que nos ocupa las reglas se definen de la siguiente manera:
c.addRule(
rpmError % negativeError,
new FuzzyConsequent(speedDelta, decreaseSpeed)
);
c.addRule(
rpmError % noError,
new FuzzyConsequent(speedDelta, keepSpeed)
);
c.addRule(
rpmError % positiveError,
new FuzzyConsequent(speedDelta, increaseSpeed)
);
Finalmente, en el bucle principal de la aplicación lo único que se hace es iterar el motor de inferencia borroso (FuzzyController::run) cada 200 milisegundos:
DDRC |= 0x80; while (true) { if (Chronometer::microseconds2 > 200000) { // each 200ms Chronometer::microseconds2 = 0; c.run(); } // turn on led when set point reached if ((RPMReader::rpm >= SET_POINT_LOW) && (RPMReader::rpm <= SET_POINT_HIGH)) PORTC |= 0x80; else PORTC &= 0x7F; }

Todo el código fuente puede descargarse de la sección soft.
Gracias, crack
Genial Avelino, teoría y práctica todo en uno.
Lo sentimos. No se permiten nuevos comentarios después de 90 días.

 Calendario
Calendario




