Detección de tonos en sistemas embebidos 
lunes, 15 de diciembre de 2014, 23:11 - Desarrollo DSP, Desarrollo Arduino, Desarrollo embebido
Cuando pensamos en detectar determinadas frecuencias o tonos en una señal lo primero que se nos viene a la cabeza suele ser la FFT, en concreto la implementación de Cooley-Tukey con N potencia de 2. La FFT está muy bien si lo que queremos es todo el espectro de una señal, pero si lo que necesitamos es detectar un único tono en una frecuencia concreta podemos recurrir al algoritmo de Goertzel, más rápido y muy fácil de implementar en sistemas embebidos.

El algoritmo de Goertzel permite calcular un coeficiente aislado de la DFT sobre un conjunto de N muestras con una complejidad temporal de O(n) y una complejidad espacial de O(1), además N no tiene por qué ser potencia de 2. Este algoritmo se basa en la aplicación de una ecuación en diferencias finitas (un filtro IIR).

A mayor N, mayor resolución en frecuencia y también mayor latencia en la detección de los tonos. Es necesario, por tanto encontrar un compromiso. La resolución en hercios del algoritmo de Goertzel viene dada por:
$$R = {f_s \over N}$$
Siendo $f_s$ la frecuencia de muestreo y $N$ el número de muestras que se evalúan en cada pasada.

1. Se calcula el índice del coeficiente correspondiente

Lo primero que hay que hacer es calcular el índice del coeficiente asociado a la DFT a partir de la frecuencia que queremos detectar:
$$k = N{f \over f_s}$$
Siendo $f$ la frecuencia que queremos detectar, $f_s$ la frecuencia de muestreo y $N$ el número de muestras que procesamos cada vez. La máxima frecuencia que podemos detectar será la mitad de la frecuencia de muestreo.

2. Para cada conjunto de N muestras

2.1. Se aplica la ecuación en diferencias

Para cada una de las muestras que van llegando, vamos aplicando la siguiente ecuación en diferencias finitas:
$$s[n] = x[n] + 2\cos\left({2 \pi k \over N}\right)s[n-1] - s[n-2]$$
$$n = 0..N$$
Con codiciones iniciales $s[-1] = s[-2] = 0$. Se trata, como se puede ver, de un sencillo filtro IIR de segundo orden.

2.2. Se obtiene del coeficiente k-esimo de la DFT

Se puede demostrar que el coeficiente k-ésimo de la DFT de tamaño N es:
$$X(k) = s[N] - W_N^ks[N-1]$$
Siendo:
$$W_N = e^{-j\left({2 \pi \over N}\right)}$$
Por tanto:
$$X(k) = s[N] - e^{-j\left({2 \pi \over N}\right)k}s[N-1]$$
Si desarrollamos la exponencial compleja mediante la fórmula de Euler tenemos que:
$$e^{-j\left({2 \pi \over N}\right)k} = \cos\left({2 \pi \over N}\right) - j \sin\left({2 \pi k \over N}\right)$$
Y, por tanto:
$$X(k)_{real} = s[N] - \cos\left({2 \pi k \over N}\right)s[N-1]$$
$$X(k)_{imag} = \sin\left({2 \pi k \over N}\right)s[N-1]$$
Para calcular la magnitud de la banda de frecuencia correspondiente calculamos el módulo de $X(k)$:
$$M^2 = \left|X(k)\right|^2 = X(k)_{real}^2 + X(k)_{imag}^2$$
De esta forma podemos medir la magnitud de la banda de frecuencia correspondiente al coeficiente k-ésimo de la DFT o, lo que es lo mismo, la magnitud de la banda de frecuencia correspondiente a la frecuencia $f$.
$$k = N{f \over f_s} \Rightarrow f = {k f_s \over N}$$

Implementación

A continuación se puede ver una implementación del algoritmo de Goertzel en Arduino:
const int ANALOG_INPUT = A0;
const int SAMPLE_RATE_HZ = 3000;
const int SAMPLE_PERIOD_US = 1000000 / SAMPLE_RATE_HZ;
const int F_HZ = 440;
const int N = 3000;
const int K = 440;  // N * F_HZ / SAMPLE_RATE_HZ;
unsigned long tPrev;

struct goertzelFilter {
  float s1, s2;
  int k, n;
  float sinv, cosv, cosv2;
  int nextIteration;
};

struct goertzelFilter filter;

void goertzelFilterReset(struct goertzelFilter &f) {
  f.s1 = 0;
  f.s2 = 0;
  f.nextIteration = 0;
}

void goertzelFilterInit(struct goertzelFilter &f, int k, int n) {
  f.k = k;
  f.n = n;
  f.cosv = cos(2 * PI * k / n);
  f.sinv = sin(2 * PI * k / n);
  f.cosv2 = 2 * f.cosv;
  goertzelFilterReset(f);
}

boolean goertzelFilterFinished(struct goertzelFilter &f) {
  return (f.nextIteration == (f.n + 1));
}

void goertzelFilterRun(struct goertzelFilter &f, float input) {
  float s = input + (f.cosv2 * f.s1) - f.s2;
  f.s2 = f.s1;
  f.s1 = s;
  f.nextIteration++;
}

float goertzelFilterGetMagnitude(struct goertzelFilter &f) {
  float real = f.s1 - (f.cosv * f.s2);
  float imag = f.sinv * f.s2;
  return ((real * real) + (imag * imag));
}

void setup() {
  Serial.begin(9600); 
  tPrev = micros();
  goertzelFilterInit(filter, K, N);
  goertzelFilterReset(filter);
}

void loop() {
  unsigned long t = micros();
  if ((t - tPrev) >= SAMPLE_PERIOD_US) {
    int v = analogRead(ANALOG_INPUT);
    if (goertzelFilterFinished(filter)) {
      float magnitude = goertzelFilterGetMagnitude(filter);
      Serial.println(magnitude);
      goertzelFilterReset(filter);
    }
    else
      goertzelFilterRun(filter, ((float) v - 512) / 512);
    tPrev = t;
  }
}

Se ha elegido una frecuencia de muestreo baja (3000Hz) para poder trabajar cómodamente con tipos float. Utilizando aritmética de punto fijo podríamos incremenentar la frecuencia de muestreo y que la detección sea más precisa.

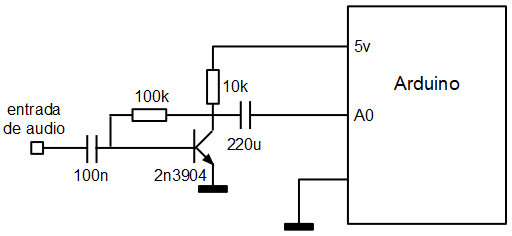
La entrada de audio se toma de la entrada analógica A0 a la que se conecta un sencillo circuito amplificador:


Elegir el valor de N

A la hora de elegir la N lo ideal es escogerla lo más grande posible, que nos permita una latencia razonable y que se cumpla que:
$$k = N{f \over f_s} \in \mathbb{N}$$
Por ejemplo, para detectar un tono de 1Khz sobre una señal muestreada a 6KHz lo ideal sería que la N valiese: 96, 102, 114… Ya que para todos estos valores se cumple que $k$ es número natural.

Magnitudes medidas para diferentes tonos

En ausencia de señal de entrada: 0.30, 0.37, 0.30, 0.35, 0.44, 0.32, 0.37, 0.28...

Con una señal de entrada de 200Hz: 2.56, 1.73, 3.56, 0.81, 0.58, 1.67, 4.71, 6.81...

Con una señal de entrada de 440Hz (la frecuencia del detector): 138.41, 87.29, 441.14, 185.20, 233.03, 762.27, 80.62, 330.98...

Con una señal de entrada de 500Hz: 25.70, 9.60, 22.50, 2.76, 16.62, 18.75, 23.56, 35.58...


Comentarios 
Lo sentimos. No se permiten nuevos comentarios después de 90 días.