Los perceptrones multicapa (Multilayer Perceptron o MLP) son redes neuronales de aprendizaje supervisado de tipo unidireccional en las que tenemos una capa de neuronas de entrada, una o más capas de neuronas intermedias y una capa de neuronas de salida. Son muy utilizadas para reconocimiento y clasificación de patrones y relativamente sencillas de implementar en sistemas embebidos utilizando aritmética de punto fijo.

En un MLP cada neurona tiene una salida y n entradas y se modela de la siguiente manera:

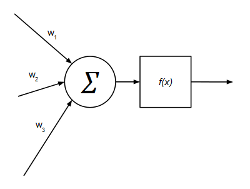
Las entradas de cada neurona suman de forma ponderada (pesos sinápticos) y dicha suma ponderada se hace pasar por una función de activación que, en el caso más general (clasificadores), se trata de la función sigmoide:
$$f(x) = {{1} \over {1+e^{-x}}}$$
Los MLP son estructuras de neuronas organizadas en forma de capas:

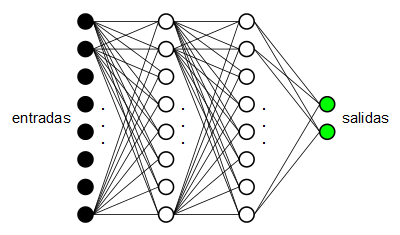
En este caso tenemos un MLP con 8 neuronas de entrada (las neuronas de entrada no son neuronas en sí, se les llama neuronas pero realmente son simplemente las entradas de la red), dos capas (denominadas “ocultas”) de 8 neuronas cada una y una capa de salida de 2 neuronas.

Los MLP con función de activación sigmoide son más utilizados para reconocimiento y clasificación de patrones. En este caso se abordará este tipo de MLP utilizando el clásico algoritmo de aprendizaje Backpropagation.

Algoritmo Backpropagation

El algoritmo Backpropagation consiste en hacer pasar por la red una serie de patrones predefinidos para los que se indica una salida “esperada”. La salida real que emite la red para cada uno de los patrones de entrada se compara con la salida “esperada” y se recalculan los pesos sinápticos hacia atrás (desde la salida hasta la entrada). De ahí el nombre del algoritmo. Los pasos de dicho algoritmo son los siguientes:

Evaluar la red

Se evalúa la red, esto es, para cada neurona desde la capa de entrada hasta la capa de salida se realiza el cálculo de los valores de salida de cada neurona utilizando la ecuación:
$$suma^{o}_{pk} = \sum_{j=1}^{L}w_{kj}^{o}y_{pj} + \theta_{k}^{o}$$
$$y_{pk}=f_{k}^{o}(suma^{o}_{pk})$$
Siendo:
$w_{kj}^{o}$ el peso sináptico de la neurona $j$ de la capa anterior sobre la neurona $k$ de la capa actual.
$f$ la función de activación (en este caso la sigmoide).

Calcular los términos del error

Para cada neurona $k$ de la capa de salida se calcula su error:
$$\delta_{pk}^{o}=(d_{pk}-y_{pk})f_{k}^{'o}(suma_{pk}^{o})$$
Siendo:
$d_{pk}$ el valor deseado para la neurona $k$ de la capa salida y para el patrón de entrada $p$.
$y_{pk}$ el valor actual de la neurona $k$ de la capa de salida para el patrón $p$.
$f'$ la derivada de la función de activación (derivada de la función sigmoide).

Mientras que para cada neurona $j$ de cada capa oculta $h$ el error hay que estimarlo a partir de los errores de la capa siguiente:
$$\delta_{pj}^{h}=f_{j}^{'h}(suma_{pj}^{h})\sum_{k}\delta_{pk}^{o}w_{kj}^{o}$$
Siendo:
$p$ el vector de entrenamiento.
$suma_{pj}^{h}$ la entrada neta (suma ponderada) de la neurona $j$ en la capa $h$ para el vector $p$.
$\delta_{pk}^{o}$ el término de error de la neurona $k$ de la capa anterior.
$w_{kj}^{o}$ el peso de la salida de la neurona $j$ de la capa anterior sobre la neurona $k$.

Actualizar los pesos

$$w_{kj}^{o}(t+1)=w_{kj}^{o}(t)+\Delta w_{kj}^{o}(t+1)$$
$$\Delta w_{kj}^{o}(t+1)=\alpha \delta_{pk}^{o}y_{pj}$$
Siendo:
$w_{kj}^{o}$ el peso de la salida de la neurona $j$ de la capa anterior sobre la neurona $k$.
$y_{pj}$ la salida de la neurona $j$ (la del extremo origen del peso $w_{kj}^{o}$).

Se repite hasta que el error sea aceptable

$$E_{p}={1 \over 2}\sum_{k}\delta_{pk}^{2}$$
Siendo:
$\delta_{pk}$ el error de la neurona $k$ de la capa de salida para el patrón de entrada $p$.

Implementación en punto fijo

En el caso de que queramos implementar una red neuronal de tipo MLP en un sistema embebido sin unidad de coma flotante, debemos intentar realizar una implementación en punto fijo de toda la operativa (tanto evaluación como aprendizaje de la red). Como se puede ver en la ecuaciones mostradas, la parte más compleja viene dada por la función de activación.
$$f(x)={1 \over {1+e^{-x}}}$$
Y por su derivada:
$$f'(x)={{e^{-x}} \over {(1+e^{-x})^2}}$$
Utilizando aproximantes de Padé de orden [3 / 3] para el cálculo de la exponencial podemos aproximar ambas funciones de forma razonablemente buena.
$$e^{x} \simeq {{1+{x \over 2}+{{x^2} \over 10}+{{x^3} \over 120}} \over {1-{x \over 2}+{{x^2} \over 10}-{{x^3} \over 120}}}$$

Para el algoritmo de entrenamiento Backpropagation es necesario utilizar la derivada de la función de activación. Esta derivada puede simplificarse y ponerse en función de la propia función sigmoide:
$$f'(x)={{e^{-x}} \over {(1+e^{-x})^2}}={1 \over {1+e^{-x}}}{{e^{-x}} \over {1+e^{-x}}}=f(x){{e^{-x}} \over {1+e^{-x}}}$$
$$f'(x)=f(x){{1+e^{-x}-1} \over {1+e^{-x}}}=f(x)\left({{1+e^{-x}} \over {1+e^{-x}}}-{1 \over {1+e^{-x}}}\right)$$
$$f'(x)=f(x)\left(1-{1 \over {1+e^{-x}}}\right)=f(x)(1-f(x))$$
Por tanto, para la función sigmoide, se cumple que:
$$f'(x)=f(x)(1-f(x))$$
Como $f(x)$ se corresponde con la salida de cada neurona (siendo $x$ la suma ponderada de sus entradas), la derivada de la salida de cada neurona puede calcularse, por tanto, de esta manera:
$$salida(1-salida)$$
En el algoritmo de entrenamiento Backpropagation esto simplifica enormemente el cálculo de los términos de error ya que se puede calcular la derivada de cada neurona a partir de su valor de salida.


Se ha utilizado como tipo funto fijo el formato Q16.16 mapeado sobre un entero de 32 bits (int32_t), esto nos da una precisión de
$$2^{-16} = 0,0000152587890625$$
Un error bastante aceptable teniendo en cuenta lo que vamos a ganar en velocidad.


Pruebas realizadas

Las pruebas se han realizado partiendo de dos patrones de entrenamiento sencillos:

$p_{1}=\{0, 0, 0, 0, 0, 1, 1, 1\}$ que debe generar la salida $\{0, 1\}$.
$p_{2}=\{0, 1, 1, 0, 0, 0, 0, 1\}$ que debe generar la salida $\{1, 0\}$.
Con los que se han obtenido muy buenos resultados:

Para el patrón $p_{1}$ se obtiene, tras el entrenamiento, la salida $$\{0.0270996, 0.972183\}$$
Para el patrón $p_{2}$ se obtiene, tras el entrenamiento, la salida $$\{0.971191, 0.0284729\}$$
Todo el código fuente puede descargarse de la sección soft.

---

Lo sentimos. No se permiten nuevos comentarios después de 90 días.

---

- Página generada en 0.0417 segundos | Site Views: 172663