El algoritmo de Ramer-Douglas-Peucker, a veces también denominado algoritmo de Douglas-Peucker a secas, es un algoritmo que fue desarrollado en los años 70 por Urs Ramer, David Douglas y Thomas Peucker. Dicho algoritmo permite reducir la cantidad de puntos en una ruta de segmentos rectilíneos utilizando un criterio de distancias. Es muy útil para la simplificación de rutas sobre mapas o para la optimización en el renderizado de imágenes vectoriales.

El algoritmo se basa en la técnica de divide y vencerás. Partiendo de una ruta inicial formada por un conjunto de N puntos, $p_0$ a $p_{n - 1}$ buscamos, de entre los puntos intermedios, el que esté más alejado de la recta que une $p_0$ y $p_{n - 1}$. Sea este punto $p_i$ y $d(i, 0, n - 1)$ la distancia entre $p_i$ y la recta que une $p_0$ con $p_{n - 1}$.

Si $d(i, 0, n - 1)$ supera un valor umbral que llamaremos $\varepsilon$, realizamos dos llamadas recursivas, una que ejecuta el algoritmo entre los puntos $p_0$ y $p_i$ y otra que ejecuta el algoritmo entre los puntos $p_i$ y $p_{n - 1}$.

Si $d(i, 0, n - 1)$ no supera el valor umbral de $\varepsilon$, descartamos de la ruta final todos los puntos intermedios entre $p_0$ y $p_{n - 1}$, esto es, descartamos todos los puntos $p_j$ tales que $i < j < n - 1$.

Con un ejemplo se ve mejor. Consideremos la siguiente ruta formada por 5 puntos, de $p_0$ a $p_4$ y consideremos un valor de $\varepsilon = 1.3$.


Inicialmente consideramos la recta que une $p_0$ con $p_4$ (el primero con el último) y buscamos el punto más alejado de ella. En nuestro caso es $p_3$ (lo he subrayado) y la distancia de la recta $\overline{p_0p_4}$ a $p_3$ es de 3.82 aproximadamente, dicho valor es superior a nuestro $\varepsilon$ (1.3) y, por tanto dividimos el problema en dos subproblemas de forma recursiva.

Invocamos, por un lado el algoritmo considerando la ruta formada por los puntos $p_0$ a $p_3$ y, por otro lado el mismo algoritmo considerando la ruta formada por los puntos $p_3$ a $p_4$. Este último caso es trivial ya que no hay puntos intermedios y, obviamente, no se puede descartar ningún punto entre $p_3$ y $p_4$.

Si consideramos ahora la ruta formada por los puntos $p_0$ a $p_3$.



Hacemos el mismo razonamiento: consideramos la recta que une el primer punto con el último ($p_0$ con $p_3$) y buscamos el punto intermedio más alejado de dicha recta. En este caso el punto más alejado de la recta que une $p_0$ con $p_3$ es $p_1$ (de nuevo subrayado) con una distancia aproximada de 1.34.

Como 1.34 es mayor que nuestro $\varepsilon$, volvemos a subdividir el problema en dos nuevos problemas más pequeños. Por un lado llamamos al algoritmo con la ruta formada por los puntos $p_0$ y $p_1$ y por otro lado llamamos al algoritmo con la ruta formada por los puntos $p_1$ a $p_3$. El cálculo del algoritmo para dos puntos, al igual que pasó anteriormente con $p_3$ y $p_4$ es trivial ya que, al no haber puntos intermedios, no es posible descartar ningún punto. Por tanto nos centraremos en el caso de la ruta entre $p_1$ y $p_3$.



Recordemos que, hasta ahora, no se ha descartado ningún punto para la ruta final. Para la ruta formada por los puntos $p_1$ a $p_3$, el punto más alejado de la recta entre $p_1$ y $p_3$ es $p_2$ con una distancia de aproximadamente 0.39. Dicha distancia sí que es menor que nuestro umbral $\varepsilon$, por tanto descartamos todos los puntos intermedios entre $p_1$ y $p_3$.



Como se puede ver, el algoritmo finalmente ha descartado el punto $p_2$ de la ruta.

A continuación se puede ver cómo sería el pseudocódigo:

ramer_douglas_peucker(vector, epsilon, izquierda, derecha)
indice := 0
max := 0
para j := (izquierda + 1) hasta (derecha - 1) hacer
    d := distancia del punto vector[j] a la recta (vector[izquierda], vector[derecha])
    si (d > max) entonces
        max := d
        indice := j
    fin si
fin para
si (max > epsilon) entonces
    ramer_douglas_peucker(vector, epsilon, izquierda, indice)
    ramer_douglas_peucker(vector, epsilon, indice, derecha)
en otro caso
    para j := (izquierda + 1) hasta (derecha - 1) hacer
        marcar vector[j] como descartado de la ruta final
    fin para
fin si

Y un ejemplo de implementación en C++ utilizando plantillas:


Para utilizar la función template hay que crear una clase que herede de RamerDouglasPeuckerPoint y que implemente, al menos, los dos métodos virtuales puros. Para puntos en el plano 2D podríamos hacer una clase de este estilo:


Esta clase implementaría el método getRamerDouglasPeuckerDistance, que devuelve la distancia entre el punto y la recta formada por los dos puntos pasados por parámetros, y el método markAsDiscarded que permite marcar puntos como descartados. Utilizando esta clase, invocar el algoritmo es tan sencillo como hacer:



A continuación puede verse el resultado de la ejecución del algoritmo sobre un perfil del continente africano formado por 28653 puntos, al que se le aplica el algoritmo con $\varepsilon = 4.5$.



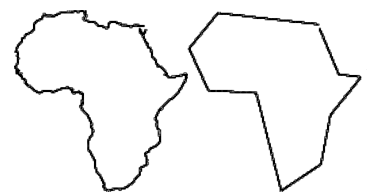
(imagen extraida de http://www.scielo.br/scielo.php?pid=S01 ... ci_arttext con licencia Creative Commons Attribution License. Sociedade Brasileira de Computação)

Código fuente en la sección soft.

---

Hey, gracias por comentar, Carlos. El algoritmo se utiliza mucho para lo que comentas de optimización de gráficos vectoriales y también en programas de seguimiento GPS (muchos de ellos almacenan varios miles de puntos): A la hora de realizar una representación visual o a la hora de realizar cálculos de ruta, muchas veces vale la pena perder precisión y ganar en velocidad al trabajar con una menor cantidad de puntos.

En efecto, el perfil del continente africano pasa de 28653 a 11 puntos.

---

Muy buena la explicación con el ejemplo (con gráficas en ASCII-art, ¡pragmático, jejeje!).
No me queda clara la utilidad, ¿obtener aproximaciones más "rectas"?
Por ejemplo en gráficos vectoriales para tener 2 versiones de un mismo gráfico: la original y otra más rápida de cargar/renderizar pero de menor calidad.

Como sugerencias, podrías poner también el nº de puntos de la figura procesada (19 creo).

---

Lo sentimos. No se permiten nuevos comentarios después de 90 días.

---

- Página generada en 0.044 segundos | Site Views: 172663